American Journal of Molecular Biology
Vol.2 No.2(2012), Article ID:18951,6 pages DOI:10.4236/ajmb.2012.22017
Solving the independent set problem by sticker based DNA computers
![]()
1Department of Pathology, Tabriz University of Medical Sciences, Tabriz, Iran
2Department of Computer Engineering, Faculty of Engineering, Isfahan University, Isfahan, Iran
3Department of Theoretical Physics and Astrophysics, Tabriz University, Tabriz, Iran
Email: *taghipourh@yahoo.com
Received 29 December 2011; revised 12 January 2012; accepted 25 January 2012
Keywords: Parallel Computing; Sticker Based DNA Computers; Independent Set Problem; NP-Complete Problem
ABSTRACT
In this paper, the sticker based DNA computing was used for solving the independent set problem. At first, solution space was constructed by using appropriate DNA memory complexes. We defined a new operation called “divide” and applied it in construction of solution space. Then, by application of a sticker based parallel algorithm using biological operations, independent set problem was resolved in polynomial time.
1. INTRODUCTION
DNA encodes the genetic information of cellular organisms. The unique and specific structure of DNA makes it one of the favorite candidates for computing purposes. In comparison with conventional silicon-based computers, DNA computers have massive degrees of miniaturization and parallelism. By recent technology, about 1018 DNA molecules can be produced and placed in a test tube. Each of these DNA molecules could act as a small processor. Biological operations such as hybridization, separation, setting and clearing can be performed simultaneously on all of these DNA strands. Thus, in an in vitro assay we could handle about 1018 DNA molecules or, we can say that 1018 data processors can be executed in parallel.
DNA computing was initially developed by Leonard Adleman in 1994 [1]. Adleman succeeded in solving seven-point Hamiltonian path problem solely by manipulating DNA molecules and suggested that DNA could be used to solve complex mathematical problems.
In 1996, a new model of DNA computing (sticker model) was introduced by Roweis et al. [2]. This model has a random access memory that requires no strand extension, uses no enzymes, and its materials are reusable. Sticker based DNA computing has potential capability for being a universal method in DNA computing. Roweis et al. also proposed specific machine architecture for implementing the sticker model as a microprocessorcontrolled parallel robotic workstation [2]. Thus, the operations used in sticker model can be performed on fully automated devices, which is helpful in reducing the error rates of operations.
In this paper, we applied sticker model for solving the independent set problem which is one of the NP-complete problems.
The paper is organized as follows. Section 2 introduces the DNA structure and various DNA computing models and discuss about Sticker based DNA computing and biological operations which are used in sticker model. Section 3 introduces a DNA based algorithm for solving the independent set problem in sticker model.
2. BASICS OF DNA COMPUTING
2.1. Structure of DNA and DNA Computing Models
DNA is a polymeric molecule which is composed of monomers called Deoxyriboneucleotides. Deoxyriboneucleotides are building blocks of DNA and each of them contains three components: sugar, phosphate group and nitrogenous base. The sugar (deoxyribose) has five carbon atoms (1’ - 5’). The phosphate group is attached to the 5’ carbon of sugar and nitrogenous base is attached to the 1’ carbon. There are four different nitrogenous bases which contribute in DNA structure: Thymine (T) and Cytosine (C) which are called pyrimidines; Adenine (A) and Guanine (G) which are called purines. Because nitrogenous bases are variable components of neucleotides, different neucleotides are distinguished by nitrogenous bases which contribute in their structure. For this reason the name of the bases are used to refer to the neucleotides, and the neucleotides are simply represented as A, G, C, and T. The neucleotides are link together by phosphodiester bonds and form single stranded DNA (ssDNA). A ssDNA molecule can be likened to a string consisting of a combination of four different symbols, A, G, C, T. Mathematically, this means we have a four letter alphabet ∑ = {A, G, C, T} to encode information. Two ssDNA molecules join together to form double stranded DNA (DsDNA) based on complementary rule: “A” from one strand bond to “T” from opposite strand, and “C” bond to “G”. In Figure 1, a schematic picture of neucleotide is shown.
DNA computing was initially developed by Leonard Adleman in 1994 [1]. Adleman resolved an instance of Hamiltonian path problem just by handling the DNA molecules. In 1995, Lipton [3] presented a method for solving the satisfiability (SAT) problem. Adleman-Lipton model can be used to solve different NP-complete problems. In Adleman-Lipton model, DNA splints are used for construction of solution space. Adleman [4,5] also presented a molecular algorithm for solving the 3-coloring problem. Chang and Guo [6-8] showed that the DNA operations in Adelman-Lipton model could be used for developing DNA algorithms to resolve the dominating set problem, the vertex cover problem, the maximal clique problem and independent set problem.
In 1996, Roweis et al. [2] introduced the Sticker based DNA computing model and applied it in solving the Minimal Set Cover problem. Perez-Jimenez and Sanchocaparrini [9] used Sticker based DNA computing to resolve knapsack problem, and this model also were applied for breaking the Data Encryption Standard (DES) [10,11]. DES encrypts 64 bit texts by using 56 bit key. Breaking DES means that given one (plain-text, ciphertext) pair, we can find a key which maps the plain-text to the cipher text. A conventional attack on DES would need to perform an exhaustive search through all of the
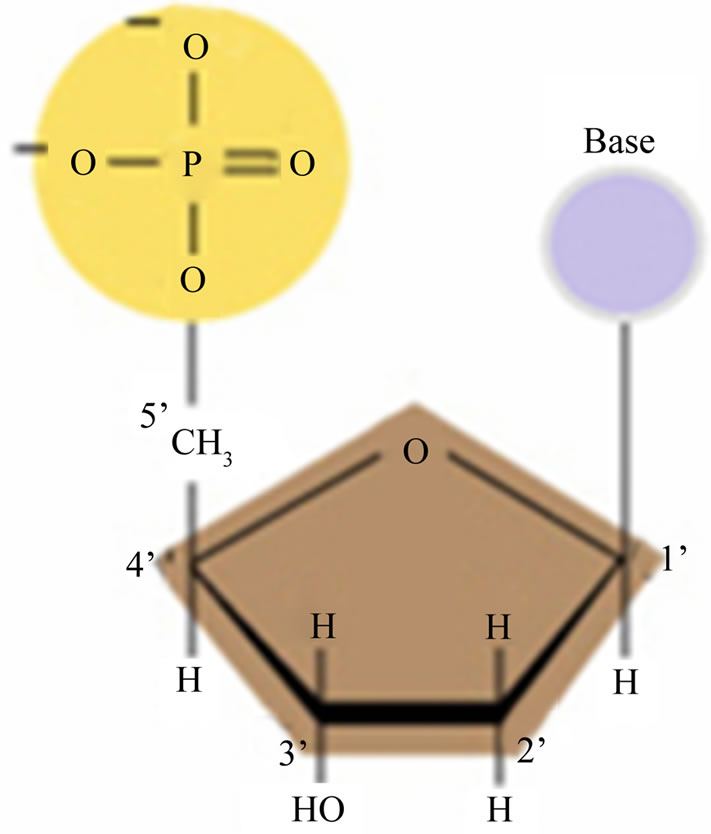
Figure 1. A neucleotide.
256 keys, which, at a rate of 100,000 operations per second, would take 10,000 years. In contrast, it was estimated that DES could be broken by using sticker based DNA computing in about 4 months.
Other than Adleman-Lipton and Sticker based models, other various models are also proposed in DNA computing by researchers. Quyang et al. [12] solved the maximal clique problem using DNA molecules and Restriction endonuclease enzymes. Amos et al. [13,14] described a DNA computation model using restriction endonuclease enzymes instead of successive cycles of separation by DNA hybridization, which can reduce the error-rate of computation. Hagiya et al. [15] proposed a new method of DNA computing that involves a self-acting DNA molecule containing both the input, program, and working memory. In this method, a single-stranded DNA molecule consists of an input segment on the 5’-end, followed by a formula (program) segment, followed by a spacer, and finally with a “head” on the 3’-end that moves and performs the computation. Another method for DNA computation is “computation by self-assembly”. Eric Winfree et al. [16-18] introduced a linear and 2-dimentional self-assembly model.
The surface-based model was introduced by Liu et al. [19]. This model uses DNA molecules attached to a solid surface, instead of DNA molecules floating in a solution. The computing by blocking was introduced by Rozenberg et al. [20,21]. This model uses a novel approach to filter the DNA molecules: Instead of separating the DNA strands to distinct tubes, or destroy and removing the DNA molecules that does not contribute to finding a solution, it blocks (inactivates) them in a way that the blocked strands can be considered as non-existent during the subsequent steps of computation.
2.2. Sticker Based DNA Computation
The sticker model was introduced by S. Roweis et al. [2]. In this model, there is a memory strand with N bases in length subdivided into K non-overlapping regions each M bases long (N ³ MK). M can be for example 20. The substrands (bit regions) are significantly different from each other. One sticker is designed for each subregion; each sticker has M bases long and is complementary to one and only one of the K memory regions. If a sticker is annealed to its corresponding region on memory strand, then the particular region is said to be on. If no sticker is annealed to a region then the corresponding bit is off. Each memory strand along with its annealed stickers is called memory complex. In sticker model, a tube is a collection of memory complexes, composed of large number of identical memory strands each of which has stickers annealed only at the required bit positions. This method of representation of information differs from other methods in which the presence or absence of a particular subsequence in a strand corresponded to a particular bit being on or off. In sticker model, each possible bit string is represented by a unique association of memory strands and stickers. This model has a random access memory that requires no strand extension and uses no enzymes [2].
Another conception in sticker model is (K, L) library. Each (K, L) library contains memory complexes with K bit regions, the first L bit regions are either on or off, in all possible ways, whereas the remaining K-L bit regions are off. The last K-L bit regions can be used for intermediate data storage. In every (K, L) library there are at least 2L memory complexes. In Figure 2, a memory complex with 7 bit regions representing the binary number 1100101 is shown.
2.3. Biological Operations in Sticker Model
There are four principal operations in sticker model: combination, separation, setting and clearing [2]. We also defined a new operation called “divide” which is used in construction of solution space. Here we briefly discuss about these operations.
1) Combine (T0, T1, T2): the memory complexes from the tubes T1 and T2 are combined to form a new tube T0, simply the contents of T1 and T2 are poured into tube T0. (T0 = T1 È T2).
2) Separate (T0, i) ® (T1, T2), this operation creates two new tubes T1 and T2, T1 contains the memory complexes having the ith bit on (T1 = +(T0, i)) and T2 contains the memory complexes having the ith bit off (T2 = –(T0, i)).
3) Set (T0, i): the ith bit region on every memory complex in tube T0 set to 1 or turned on, or we can say the sticker for that bit is annealed to corresponded bit region on every memory complex.
4) Clear (T0, i): the ith bit region on every memory complex in tube T0 set to 0 or turned off, or we can say the stickers of that bit region must be removed (if present) from every memory complex in tube T0.
5) Divide (T0, T1, T2): by this operation, the contents of tube T0 is divided into two equal portions and poured into the tubes T1 and T2.
3. SOLVING THE INDEPENDENT SET PROBLEM IN STICKER BASED DNA COMPUTERS
3.1. Definition of the Independent Set Problem
In graph theory, an independent set of a graph G = (V, E),

Figure 2. A memory complex representing 1100101.
where V is the set of the vertices and E is the set of the edges, is a subset V1 Í V such that no two vertices in V1 are joined by an edge in E. On the other hand, the independent set is a set of vertices such that for every two vertices, there is no edge connecting the two. The size of an independent set is the number of vertices it contains. A maximum independent set is a largest independent set for a given graph G and the problem of finding such a set is called the maximum independent set problem. The maximum independent set problem has been proved to be a NP-complete problem [22]. For example, the graph in Figure 3 includes 5 vertices and 4 edges.
All of the independent sets for our graph are as follows: {V1}, {V2}, {V3}, {V4}, {V5}, {V1, V2}, {V1, V3}, {V1, V4}, {V2, V3}, {V3, V5}, {V4, V5}, {V1, V2, V3}
It is clear that the independent set of the maximum size is {V1, V2, V3}, furthermore, the size of the independent set problem in our graph is 3.
3.2. Construction of Sticker Based DNA Solution Space for Independent Set Problem
First of all, it is essential to generate the sticker based DNA solution space of our problem. Then, basic biological operations are used to select legal strands and remove illegal strands from the solution space. It is obvious that a graph with N vertices has 2N subset of vertices or 2N possible independent sets. Furthermore, each possible independent set can be represented by an Ndigit binary number. If the ith bit in an N-digit binary number is set to 1, it represents that the ith vertex is in the independent set. If the ith bit in an N-digit binary number is set to 0, it represents that the ith vertex is not in the independent set.
Our graph has 5 vertices and 32 possible independent sets. All of these possible independent sets can be represented by a 5-digit binary number. For example the binary number 11100 represent the {V1, V2, V3} or the binary number 11111 represent the {V1, V2, V3, V4, V5}.
To represent all possible independent sets by appropriate DNA memory complexes, we introduce two methods for construction of solution space.
Method One:
In this method which is proposed by Roweis et al., [2]
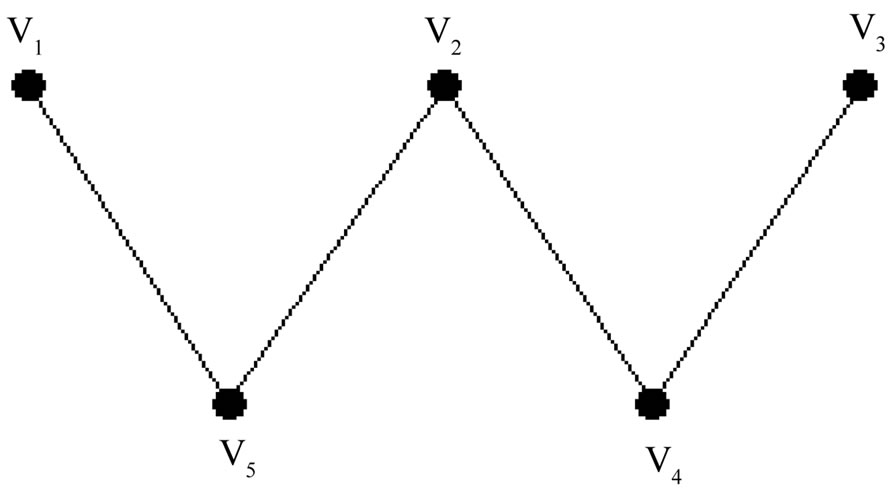
Figure 3. The graph of our problem.
first we provide enough amounts of memory strands with at least 5 bit regions. Then, the strands are split into two tubes A and B. To one tube (tube A) is added an excess amounts of all stickers and set all bits on. The unused stickers are then removed. The contents of tubes A and B are then mixed together and by rising temperature all annealed stickers dissociate from memory strands. Finally the mixture is cooled again, causing the stickers to randomly anneal to the memory strands. By this method, it is expected that approximately 63% of memory complexes will be produced. Of course, this percentage can obviously be increased by starting with more memory strands. The advantage of this method is that the solution space is produced at single step, but its main disadvantage is that some memory complexes may not be produced by above method.
Method Two:
1) Input (T0), where T0 contains large amounts of memory strands with at least N (number of vertices in graph) bit regions.
2) For i = 1 to N, where N is number of vertices in graph a) Divide (T0, T1, T2)
b) Set (T1, i)
c) Combine (T0, T1, T2)
End for Note: Method two has N divide, N set and N combine operations. At the end of procedure, tube T0 contains all of the memory complexes which each of them represent one of the possible independent sets. The main advantage of this new method is that the memory complexes representing all possible independent sets will be produced definitely. In our example, tube T0 contains 32 different memory complexes. The 32 memory complexes which are produced during construction of solution space are shown in Table 1.
3.3. DNA Algorithm for Solving the Independent Set Problem
The following algorithm is proposed for solving the independent set problem:
1) For k = 1 to m, where m is the number of edges in the graph G a) Let ek = (vi, vj), where ek is one edge and vi, vj are vertices which are connected to each other by ek
b) Bit regions i and j represents vi and vj, respectively.
c) Separate (T0, i) → (T1, T2)
d) Separate (T1, j) → (T3, T4)
e) Discard T3
f) Combine (T0, T2, T4)
2) For i = 0 to n – 1 For j = i down to 0 Separate (Tj, I + 1) → (T(j+1)’, Tj)



Table 1. Memory complexes which are produced during construction of solution space.
Combine (Tj+1, Tj+1, T(j+1)’)
3) Read Tn; else if it was empty then:
Read Tn–1; else if it was empty then:
Read Tn–2; else if it was empty then:
Read T2; else if it was empty then:
Read T1;
According to the steps in the algorithm, the independent set problem can be resolved by sticker based DNA computation in polynomial time. Any two vertices connected in the graph G cannot be the members of the same independent set; hence their corresponding bit regions cannot be set to 1. For example, we have four edges in our graph: (v1, v5), (v2, v5), (v2, v4), (v3, v4), therefore “1xxx1”, “x1xx1”, “x1x1x” and “xx11x” (x can be either 1 or 0) cannot be independent set and memory complexes representing them should be removed from solution space.
Step 1 of the algorithm is executed m times (m is 4 in our graph) and at each round of execution the memory complexes representing the subsets “1xxx1”, “x1xx1”, “x1x1x” and “xx11x” are removed from tube T0. At the end of step 1, illegal memory complexes are removed from solution space and tube T0 only contains the memory complexes which represent legal independent sets. ({V1}, {V2}, {V3}, {V4}, {V5}, {V1, V2}, {V1, V3}, {V1, V4}, {V2, V3}, {V3, V5}, {V4, V5}, {V1, V2, V3}).
By the execution of step 2, the memory complexes without any annealed stickers are placed in tube T0, the memory complexes with only one annealed sticker are placed in tube T1, the memory complexes with 2 annealed stickers are placed in tubes T2, the memory complexes with 3 annealed stickers are placed in tube T3, and so on. Note, that the numbers of annealed stickers in every memory complex represent the number of vertices in corresponding independent set. For example, in Graph of our problem, the legal independent sets with one vertex ({V1}, {V2}, {V3}, {V4}, {V5}) are placed in tube T1 , and those with 2 vertices ({V1,V2}, {V1,V3}, {V1,V4}, {V2,V3}, {V3,V5}, {V4,V5}) are placed in tube T2 and finally the independent set with 3 vertices ({V1,V2,V3}) is placed in tube T3.
The legal memory complexes which remain in tube T0 at the end of step 1 of the algorithm and their final places at the end of step 2 are shown in Table 2.
In step 3, all of the tubes (from Tn to T1) are evaluated for presence of memory complexes, and the first tube which is not empty and contains memory complexes represent maximum independent set. In our example, tubes T5 and T4 are empty and devoid of any memory complexes. The first tube which contains DNA molecules is tube T3. As mentioned before, the memory complexes in tube T3 have 3 annealed stickers; therefore, the maximum independent set in our graph is 3.
4. CONCLUSIONS
In this paper, the sticker based DNA computing was used for solving the independent set problem. This method could be used for solving other NP-complete problems. There are four principal operations in sticker model: Combination, Separation, Setting and Clearing. We also defined a new operation called “divide” and applied it in construction of solution space. This new method of construction of solution space has some advantages over other methods. The main advantage of this new method is that the memory complexes representing all possible independent sets will be produced definitely.

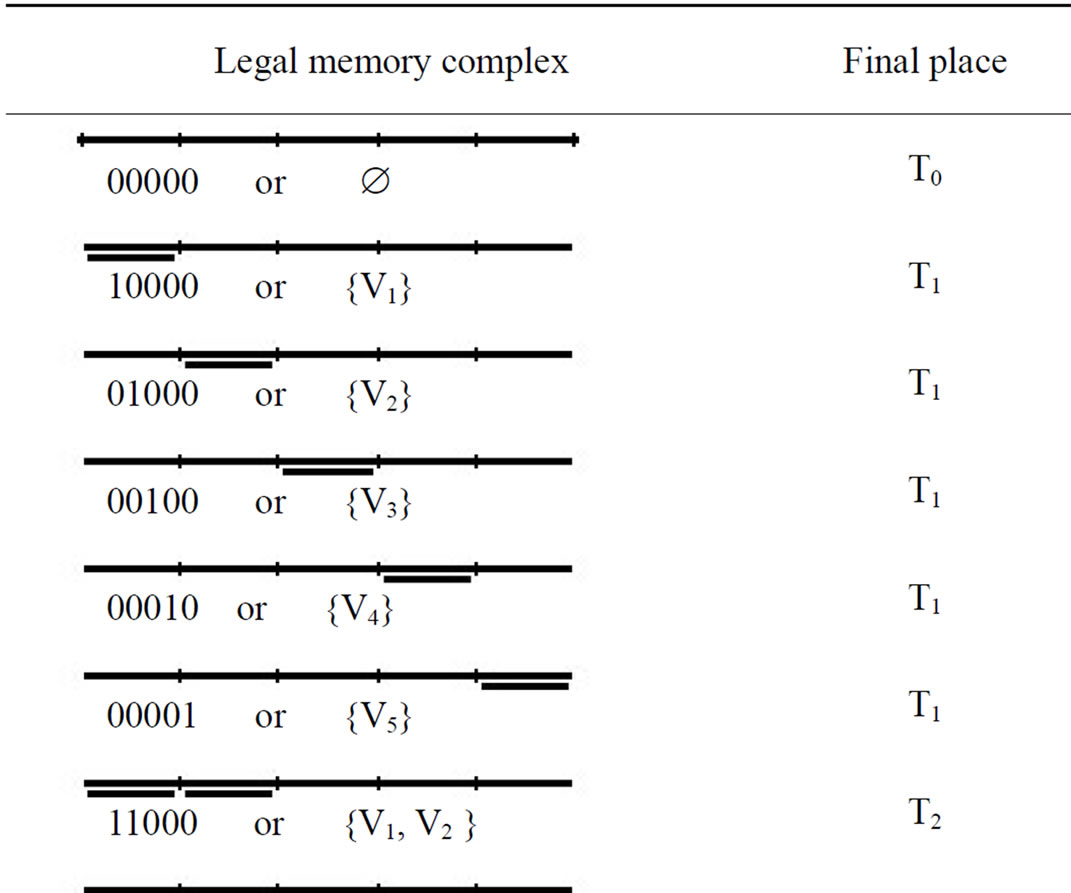
Table 2. The legal memory complexes which remain in tube T0 at the end of step 1 of algorithm and their final places at the end of step 2.
Among the four principal operations in sticker model, “Clearing” operation is the most problematic and there are some difficulties and limitations in perfect execution of that. For this reason, we have not used this operation in our algorithm.
REFERENCES
- Adleman, L.M. (1994) Molecular computation of solutions to combinatorial problems. Science, 266, 1021-1024. doi:10.1126/science.7973651
- Roweis, S., et al. (1999) A sticker based model for DNA computation. In: Landweber, L. and Baum, E., Eds., The 2nd Annual Workshop on DNA Computing, Princeton University, Series in Discrete Mathematics and Theoretical Computer Science, DIMACS, American Mathematical Society, 1-29.
- Lipton, R.J. (1995) DNA solution of hard computational problems. Science, 268, 542-545. doi:10.1126/science.7725098
- Adleman, L.M. (1995) On constructing a molecular computer. University of Southern California, Los Angeles, 1995.
- Adleman, L.M. (1996) On constructing a molecular computer. In: Lipton, R.J. and Baum E.B., Eds., DNA Based Computers, American Mathematical Society, 1-22.
- Chang, W.-L. and Guo, M. (2002) Solving the dominating-set problem in Adleman—Lipton’s model. The 3rd International Conference on Parallel and Distributed Computing, Applications and Technologies, Kanazawa, 4-6 September 2002, 167-172.
- Chang, W.-L. and Guo, M. (2002) Solving the clique problem and the vertex cover problem in Adleman— Lipton’s model. IASTED International Conference, Networks, Parallel and Distributed Processing, and Applications, Japan, 2-4 July 2003, 431-436.
- Chang, W.-L. and Guo, M. (2002) Solving NP-complete problem in the Adleman—Lipton model. The Proceedings of 2002 International Conference on Computer and Information Technology, Japan, 157-162.
- Perez-Jimenez, M.J. and Sancho-Caparrini, F. (2001) Solv- ing knapsack problems in a sticker based model. Series in Discrete Mathematics and Theoretical Computer Science, Seventh Annual Workshop on DNA Computing, Princeton University, Series in Discrete Mathematics and Theoretical Computer Science, DIMACS, American Mathematical Society.
- Adleman, L., Rothemund, P., Roweis, S. and Winfree E. (1999) On applying molecular computation to the data encryption standard. The 2nd Annual Workshop on DNA Computing, Princeton University, Series in Discrete Mathematics and Theoretical Computer Science, DIMACS, American Mathematical Society, 31-44.
- Boneh, D., Dunworth, C. and Lipton, R. (1996) Breaking DES using a molecular computer. Technical Reports, TR- 489-95, Princeton University, Princeton.
- Quyang, Q., Kaplan, P.D., Liu, S. and Libchaber, A. (1997) DNA solution of the maximal clique problem. Science, 278, 446-449. doi:10.1126/science.278.5337.446
- Amos, M., Gibbons, A. and Hodgson, D. (1996) Error-resistant implementation of DNA computations. Proceedings of the 2nd DIMACS Workshop on DNA Based Computers, 87-101.
- Amos, M., Gibbons, A. and Hodgson, D. (1996) A new model of DNA computation. 12th British Colloquium on Theoretical Computer Science.
- Hagiya, M., Arita, M., Kiga, D., Sakamoto, K. and Yokoyama, S. (1999) Towards parallel evaluation and learning of boolean μ-formulas with molecules. DIMACS: Series in Discrete Mathematics and Theoretical Computer Science, Proceedings of 3rd Annual Meeting on DNA Based Computers, 48, 105-114.
- Winfree, E. (1998) Simulations of computing by selfassembly. In: Winfree, E. and Gifford, D.K., Eds., 4th International Meeting on DNA Based Computers, Massachusetts Institute of Technology, Cambridge, 213-239.
- Winfree, E., Liu, F.L., Wenzler, L.A. and Seeman, N.C. (1998) Design and self-assembly of two-dimensional DNA crystals. Nature, 394, 539-544. doi:10.1038/28998
- Winfree, E., Yang, X. and Seeman, N.C. (1996) Universal computation via self-assembly of DNA: Some theory and experiments. Proceedings of the 2nd DIMACS Workshop on DNA Based Computers, 44, 191-213.
- Liu, Q., et al. (1996) A surface-based approach to DNA computation, Proceedings of the 2nd Annual Meeting on DNA Based Computers, Princeton University, Princeton, 10-12 June 1996.
- Rozenberg, G. and Spaink, H. (2003) DNA computing by blocking. Theoretical Computer Science, 292, 653-665. doi:10.1016/S0304-3975(01)00194-3
- Schmidt, K., Henkel, C., Rozenberg, G. and Spaink, H. (2001) Experimental aspects of DNA computing by blocking: Use of fluorescence techniques for detection. In: Kraayenhof, R., Visser, A.J.W.G. and Gerritsen, H.C., Eds., Fluorescence Spectroscopy, Imaging and Probes. Springer- Verlag, Berlin.
- Garey, M.R. and Johnson, D.S. (1979) Computer and intractability: A Guide to the theory of NP-completeness. Freeman, San Francisco.
NOTES
*Corresponding author.

