American Journal of Operations Research
Vol.05 No.05(2015), Article ID:59473,7 pages
10.4236/ajor.2015.55033
Multi-Knapsack Model of Collaborative Portfolio Configurations in Multi-Strategy Oriented
Shujuan Luo, Sijun Bai, Suike Li
School of Management, Northwestern Polytechnical University, Xi’an, China
Email: luosj@mail.nwpu.edu.cn, baisj@nwpu.edu.cn, lisk@mail.nwpu.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 July 2015; accepted 6 September 2015; published 9 September 2015
ABSTRACT
Aiming at constructing the multi-knapsack model of collaborative portfolio configurations in multi-strategy oriented, the hybrid evolutionary algorithm was designed based on greedy method, combining with the organization of the multiple strategical guidance and multi-knapsack model. Furthermore, the organizing resource utility and risk management of portfolio were considered. The experiments were conducted on three main technological markets which contain communication, transportation and industry. The results demonstrated that the proposed model and algorithm were feasible and reliable.
Keywords:
Multi Knapsack Model, Multi Strategy, Collaborative Portfolio, Evolutionary Algorithm

1. Introduction
In the practical competitions, in order to reduce the operational risk and obtain certain profit space in the new field, many enterprises will choose the diversified development strategy. However, it is proved that numerous organizations did not gain the expected return in the diversification process. The reasons are the mistake of making strategy and the implementation difficulty of diversification strategy. Applying the theory of portfolio management and system method to the implementation of diversification strategy could improve the capability of strategy implementation and achieve the target of the organization diversification strategy. Meantime, the organization will encounter a variety of project opportunities in the expanding process of diversification. Facing numerous alternative projects, how to select and configure them is the urgent problem needed to be solved.
A successful implementation of project cannot do without the guidance of project organization strategy. Diversification of project portfolio selection and configuration must conform with the organization strategy, at the same time, the multi-strategy requires a specific project and project portfolio selection to achieve. Through the analysis of diversification strategy, our conclusion is that every implementation way, based on the diversi- fication strategy, can be regarded as a project management process, and each new work can be managed and realized as a new project. Therefore, taking the project portfolio allocation concept to realize the diversification of organizational strategy is effective and necessary [1] . The success of diversification of organizational strategy not only depends on the success or failure of individual project, but also depends on the evaluation, selection, configuration and benefits of the project portfolio [2] [3] . This paper is the study of multiple strategic orientation and resource limited project portfolio allocation problem, the goals are: 1) by portfolio allocation to achieve organizational gross income maximum, portfolio risk minimum; 2) to solve the problem of stability and coordi- nation among project portfolios.
2. Assumptions of the Questions of Collaborative Portfolio Configurations in Multi-Strategy Oriented
In reality, the decision of the diversification strategy must consider whether there are good projects, long-term growth prospects and their own ability of resources. For this, considerable theoretical researches and enterprise management practices were made. For example, Fu Jun, one entrepreneur, proposed, when carrying out the projects or target industries which multiple choices would enter, we must carefully analyze the following basis for decision: First is the potential of the selected projects and industry to become bigger and stronger rapidly. If the market capacity of the project industry is limited, too scattered or difficult to expand, it is unfavorable to choose. Second is the sustained development prospect of the selected projects and industry. Although some selected projects and industry have the potential to become bigger and stronger and meet the first basis, they may be eliminated because of the lack of the possibility to develop for a long time. Finally, do the new executive projects and the project combination fit the organization’s reserve capacity of existing resources? The assumptions of diversification decisions of Founder are as followed. One is the traditional and stable project. Selecting the base project whose income is relatively stable to ensure that it can continue making stable earnings for the group and reduce the adverse impact of the economic fluctuation. The other is a high-tech project. Through the project selection and execution to master the key technology in the new field, set the key tech- nology as a prime mover of the sustained development of the group [4] .
This paper built the portfolio allocation model guiding by the pluralistic strategy. The specific problems were briefly described as follows. Assuming the diversification strategy of high-level decisions of the organization decided to achieve the pluralistic strategy by projecting and the project portfolio management. On the basis of allocating the organizational resources, m portfolios were established. According to the demand of the pluralistic strategy, the organizational resource type and quantity which each project portfolio can allocate were limited. The organization prepared n projects. Under certain constraints, these projects were selected to these com- binations, achieving the biggest implementation of the strategic goals. In view of the complexity of the com- bination and allocation of the projects in the diversifying strategy oriented, to simplify the complex problems and build the model consistent with the actual situation of the organization, we need make assumptions on the following problems:
2.1. Resource Sharing
Based on the analysis of organizational diversification strategy classification and resource requirements, and the project portfolio allocation of the sub strategy in the multi-strategy, project resource sharing is widespread and is the prerequisite for scale effect. Project resource sharing illustrates the soft constraints of resources of the project portfolio are the key characteristics which distinguish this from the hard constraints of the traditional knapsack problems knapsack and goods size. The project resource sharing is related to the property of the resources. Non-consumption resources, such as the fixed assets, are relatively more likely to be shared. In addition, it is related to the project similarity of the portfolio. If the similarity degree is high, the possibility of resource sharing is relatively large. The number of the configuration of the project is concerned. The more projects the same combination executes, the higher degree of resource sharing could be.
Since the references are less, the measurement of the total amount of resource sharing is difficult. According to the above analysis, the following relevant assumptions are taken:
i) The sharing degree of the resource k can be expressed as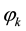 , means consumable resources cannot be shared. Means resources can be fully shared (such as fixed assets);
, means consumable resources cannot be shared. Means resources can be fully shared (such as fixed assets);
ii) The resource which the resource k allocate for the project portfolio j is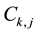 , the similarity of project portfolio j is
, the similarity of project portfolio j is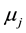 ,
, 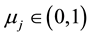 ,
, 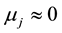 means the projects are completely different.
means the projects are completely different. 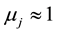 means the projects are almost same but there is no same projects exactly. So
means the projects are almost same but there is no same projects exactly. So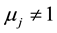 .
.
The implementation number of the project portfolio j is . The sharing coefficient
. The sharing coefficient 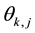 and sharing amount of
and sharing amount of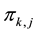 , which belong to the resource k in the project portfolio j, are calculated by:
, which belong to the resource k in the project portfolio j, are calculated by:
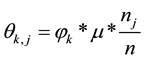 (1)
(1)
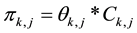 (2)
(2)
In the project portfolio allocation model, the resource constraints should be adjusted according to the organizational strategy, project portfolio and the project portfolio resource sharing accounting of the resource characteristics.
2.2. Risk Management
The project portfolio allocation of the multi-strategy oriented need consider the overall portfolio risks. The first step is risk identification, analysis and assessment of individual projects, but the project portfolio risk of the organization cannot be the simple sum of each individual objective risk. The difficulty of the risk management of the organization project combination should also be considered. The difficulty of the project portfolio management is related to the similarity between the projects, which means if the difficulty of the risk management is low, the overall risk will be reduced. At the same time, it is related to the number of the selected project portfolio. The more items the same portfolio executes, the more difficult the risk management of project portfolio is. Meantime, the risk of portfolio configuration will increase.
Ditto, the risk tolerance of project portfolio j is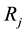 . Assume that the similarity of project portfolio j is
. Assume that the similarity of project portfolio j is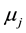 , and the implementation number of project portfolio j is
, and the implementation number of project portfolio j is .
. 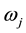 means the difficulty of the risk management coefficient and the risk increase of the project portfolio j is
means the difficulty of the risk management coefficient and the risk increase of the project portfolio j is


According to the Formula (3) and (4), we can obtain some conclusions. If






3. The Multi-Knapsack Model and Algorithm Design of Portfolio Collaborative Configuration
3.1. The Multi-Knapsack Model of Portfolio Collaborative Configuration
1) the explanations of the symbols
Corresponding to the diversification strategy of the organization, the number of the established configuration project portfolio j is








2) the objective function and the constraint conditions








In the formulas, the multi knapsack model of the portfolio allocation (5) is a 0 - 1 integer programming [6] . The all solutions of this model are the matrix space of




3.2. Greedy Method―Genetic Algorithm Design
The problem of the simple genetic algorithm is that when it faces the larger solution model, it is possible that all the individual values are 0 and Iterative could interrupt. Therefore, the greedy algorithm is consulted and introduced to initialize the groups and repair the unfeasible solution. Combining the SGA with the traditional greedy algorithm, the search speed and the accuracy of the algorithm are improved. Furthermore, it can over- come the problem of being easy to fall into local optimum, which is one disadvantage of the traditional method [7] [8] .
1) the genetic coding and fitness function
Treat with the integer coding. For example, coding for the multiple knapsack problem, which contains 20 projects and 3 portfolios. It can be expressed as the following integer set:


The fitness function is defined as
values are arranged by ascending. Treat the number of original adaptive value as the new adaptive value and change the scale of the adaptive value. The purpose of doing so is to reduce the probability of the premature convergence or stop of the iteration.
2) the genetic operator and the algorithm flow
First of all, use the completely random method to initialize the population. And then repair the unfeasible solution. Secondly, based on the greedy method to produce an approximate optimal solution, replace the worst individual of the population with it to get an optimization Initial population. The algorithm flow is as shown in Figure 1.
4. Case Analysis and Conclusions
4.1. The Description of Case Background
The headquarters of company Z decided to change the position of Chinese Company, and help it become the product research and development, processing, manufacturing and comprehensive service base of the Asia Pacific region. According to its core competence and diversification development strategy, it formulated a diversification strategy. The diversification strategy, namely the 3 technologies: radio frequency technology (HF), optical fibre technology (FO), cable and polymer technology (NF) and 3 application areas, namely the three main markets: Communication, Transportation, industry [9] . Taking one technical field of Z company in three Chinese market (“1 × 3”) as the research object to carry out diversification analysis. Transform it into a mathematical model of the multi knapsack problem, which contains 3 backpack (portfolios) and 20 items (alternative projects) and then establish the project portfolio collaborative allocation model in the diversification strategy-oriented. Finally, analyze the dynamic process of allocation and coordination of the project portfolio.
4.2. Basic Data Input
In order to verify the effectiveness of the model and algorithm, this paper combined with the actual situation of Z company, and simulated project portfolio allocation problems. In this simulation, there are 3 portfolio (m = 3), 20 items (n = 20) and 2 kinds of resources (k = 2). Assume that the degree of resource sharing are

Figure 1. Hybrid genetic algorithm flow chart.
Table 1. The parameters of portfolio configuration.
Table 2. The parameters of candidate item.
4.3. Experiment Results
The parameters of the hybrid evolutionary algorithm can be set as follows: the number of the population size, i.e. individual species, is Nind = 30. The maximum number of the evolutionary generation is Maxgen = 100. The crossover rate is cr = 0.1, and the mutation rate is mr = 0.1. The results of the portfolio configurations in multi-strategy oriented, which are presented in the Table 3, can be gained through the MATLAB.
As is shown in Table 3, the usage of organizing project resource should reduce the total cost of resource. Considering the difficulty of the risk management of the project portfolio, the portfolio risk is the adjustment. The results illustrate that the sum of project is 17, and the organizing strategical value confirmed by three joint projects is 907. It shows that we have proposed the model and method which can fulfill the target which makes the organizing strategical value the most based on the share and rational allocation of resources. We consider the ability to withstand risk, simultaneously. Project optimum population and the trend of average population along with the change of evolutionary generation are shown in Figure 2. It demonstrates that the proposed model and algorithm could gain the global best solution of the joint project portfolios. It also validates that the presented method turns out to be an efficient and steady one.
5. Conclusion
The paper has proposed a novel thought based on multi-organization and project portfolio. Strategy implemen- tation and project portfolio management theory have provided the opportunity to organize the multiple strategies and to guide the project portfolio. Combing with the case of company Z, we constructed the multi-knapsack
Figure 2. The change trend of the optimal value and the population mean with the evolution generation.
Table 3. The results of project portfolio.
model of collaborative portfolio configurations in multi-strategy oriented and proposed the hybrid evolutionary algorithm based on the greedy method which succeeds in solving the problem of multiple strategical guidance and project portfolio. The experiment presents the statistical data and shows the feasibility of the proposed model and method.
Acknowledgements
We thank the Editor and the referee for their comments. This paper is supported by National Natural Science Foundation of China under Grant No. 71172123, by Aviation Science Fund under Grant No. 2012ZG53083.
Cite this paper
ShujuanLuo,SijunBai,SuikeLi, (2015) Multi-Knapsack Model of Collaborative Portfolio Configurations in Multi-Strategy Oriented. American Journal of Operations Research,05,401-408. doi: 10.4236/ajor.2015.55033
References
- 1. Su, L.Y. (2008) The Implementation of Enterprise Diversification Management and Project Management. Inner Mongolia Science Technology and Economy, 14, 278-281.
- 2. Li, S.K., Bai, S.J., Guo, Y.T. and Wang, X.B. (2014) A Study on Distributed Collaborative Model of Model Development Based on Logistics. Industrial Engineering Journal, 17, 50-54.
- 3. Shen, J. (2009) Analysis on Synergy Effects in Diversification Strategy of Enterprises. Economy and Management, 23, 49-54.
- 4. Shi, Y.H. (2005) The Empirical Analysis on the Diversified Profession Selection. SCI/TECH Information Development and Economy, 17, 76-79.
- 5. Song, H.S., Fu, R.Y., Xu, R.S. and Song, H.Z. (2009) Hybrid Genetic Algorithm for Multi-Knap Sack Problem. Computer Engineering and Applications, 45, 45-48.
- 6. Shi, L., Zhang, Y.H. and Lv, J.H. (2013) Optimization Algorithm of 0-1 Knapsack Problem Based on Absolute greedy and Expected Efficiency. Application Research of Computers, 11, 1-5.
- 7. Li, Z.Y., Ma, L. and Zhang, H.Z. (2013) Application of Bat Algorithm in Multi-Objective and Multi-Choice Knapsack Problem. The Computer Simulation, 30, 350-354.
- 8. Zhang, T.N. and Zeng, Q.C. (2003) Business Reengineering and Synergetic Development. Management Sciences in China, 16, 21-24.
- 9. Zhang, X.F. (2011) The Development of HUBER+SUHNER in China. Intelligent Building and City Information, 8, 104-105.




