ABSTRACT

In this paper, the problem of non-response with significant travel costs in multivariate stratified sample surveys has been formulated of as a Multi-Objective Geometric Programming Problem (MOGPP). The fuzzy programming approach has been described for solving the formulated MOGPP. The formulated MOGPP has been solved with the help of LINGO Software and the dual solution is obtained. The optimum allocations of sample sizes of respondents and non respondents are obtained with the help of dual solutions and primal-dual relationship theorem. A numerical example is given to illustrate the procedure.

Keywords:Geometric Programming, Fuzzy Programming, Non-Response with Travel Cost, Optimum Allocations, Multivariate Stratified Sample Surveys

1. Introduction

In sampling the precision of an estimator of the population parameters depends on the size of the sample and variability among the units of the population. If the population is heterogeneous and size of the sample depends on the cost of the survey, then it is likely to be impossible to get a sufficiently precise estimate with the help of simple random sampling from the entire population. In order to estimate the population mean or total with greater precision, the heterogeneous population is divided into mutually-exclusive, exhaustive and non-overlapping strata which will be more homogeneous than the entire population. The entire population is called Stratified Random Sampling. The problem of optimum allocation in stratified random sampling for univariate population is well known in sampling literature; see for example Cochran [1] and Sukhatme et al. [2] . In multivariate stratified sample surveys problems the non-response can appear when the required data are not obtained. The problem of non-response may occur due to the refusal by respondents or their not being at home, making the information of sample inaccessible. The problem of non-response occurs in almost all surveys. The extent of nonresponse depends on various factors such as type of the target population, type of the survey and the time of survey. For the problem of non-response in stratified sampling it may be assumed that every stratum is divided into two mutually exclusive and exhaustive groups of respondents and non respondents.

Hansen and Hurwitz [3] presented a classical non-response theory which was first developed for surveys in which the first attempt was made by mailing the questionnaires and a second attempt was made by personal interviews to a sub sample of the non respondents. They constructed the estimator for the population mean and derived the expression for its variance and also worked out the optimum sampling fraction among the non respondents. El-Badry [4] further extended the Hansen and Hurwitz’s technique by sending waves of questionnaires to the non respondent units to increase the response rate. The generalized El-Badry’s approach for different sampling design was given by Foradori [5] . Srinath [6] suggested the selection of sub samples by making several attempts. Khare [7] investigated the problem of optimum allocation in stratified sampling in presence of nonresponse for fixed cost as well as for fixed precision of the estimate. Khan et al. [8] suggested a technique for the problem of determining the optimum allocation and the optimum sizes of subsamples to various strata in multivariate stratified sampling in presence of non-response which is formulated as a Nonlinear Programming Problem (NLPP). Varshney et al. [9] formulated the multivariate stratified random sampling in the presence of non-response as a Multi-objective Integer Nonlinear Programming problem and a solution procedure is developed using lexicographic goal programming technique to determine the compromise allocation. Fatima and Ahsan [10] addressed the problem of optimum allocation in stratified sampling in the presence of non-response and formulated as an All Integer Nonlinear Programming Problem (AINLPP). Varshney et al. [11] have considered the multivariate stratified population with unknown strata weights and an optimum sampling design is proposed in the presence of non-response to estimate the unknown population means using DSS strategy and developed a solution procedure using Goal Programming technique and obtained an integer solution directly by the optimization software LINGO. Raghav et al. [12] has discussed the various multi-objective optimization techniques in the multivariate stratified sample surveys in case of non-response.

Geometric Programming (GP) is a smooth, systematic and an effective non-linear programming method used for solving the problems of sample surveys, management, transportation, engineering design etc. that takes the form of convex programming. The convex programming problems occurring in GP are generally represented by an exponential or power function. GP has certain advantages over the other optimization methods because it is usually much simpler to work with the dual than the primal one. The degree of difficulty (DD) plays a significant role for solving a non-linear programming problem by GP method.

Geometric Programming (GP) has been known as an optimization tool for solving the problems in various fields from 1960’s. Duffin, Peterson and Zener [13] and also Zener [14] have discussed the basic concepts and theories of GP with application in engineering in their books. Beightler, C.S., and Phililps, D.T. [15] , have also published a famous book on GP and its application. Davis and Rudolph [16] applied GP to optimal allocation of integrated samples in quality control. Ahmed and Charles [17] applied geometric programming to obtain the optimum allocation problems in multivariate double sampling. Ojha, A.K. and Das, A.K. [18] have taken the MultiObjective Geometric Programming Problem being cost coefficient as continuous function with weighted mean and used the geometric programming technique for the solutions. Maqbool et al. [19] and Shafiullah et al. [20] have discussed the geometric programming approach to find the optimum allocations in multivariate two-stage sampling and three-stage sample surveys respectively.

In many real-world decision-making problems of sample surveys, environmental, social, economical and technical areas are of multiple-objectives. It is significant to realize that multiple objectives are often non-commensurable and in conflict with each other in optimization problems. The multi-objective models with fuzzy objectives are more realistic than deterministic of it. The concept of fuzzy set theory was firstly given by Zadeh [21] . Later on, Bellman and Zadeh [22] used the fuzzy set theory for the decision-making problem. Tanaka et al. [23] introduces the objective as fuzzy goal over the α-cut of a fuzzy constraint set and Zimmermann [24] gave the concept to solve multi-objective linear-programming problem. Biswal [25] and Verma [26] developed fuzzy geometric programming technique to solve Multi-Objective Geometric Programming (MOGP) problem. Islam [27] [28] has discussed modified geometric programming problem and its applications and also another fuzzy geometric programming technique to solve MOGPP and its applications. Fuzzy mathematical programming has been applied to several fields.

In this paper, we have formulated the problem of non-response with significant travel cost where the cost is quadratic in 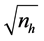in multivariate stratified sample surveys as a Multi-Objective Geometric Programming problem (MOGPP). The fuzzy programming approach has been described for solving the formulated MOGPP and the optimum allocations of sample sizes of respondents and non respondents are obtained. A numerical example is given to illustrate the procedure.

2. Formulation of the Problem

In stratified sampling the population of N units is first divided into L non-overlapping subpopulation called strata, of sizes with 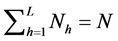and the respective sample sizes within strata are drawn with independent simple random sampling denoted by with

Let for the 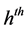stratum:

: Stratum size.

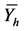: Stratum mean.

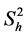: Stratum variance.

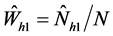: the estimated stratum weight among respondents.

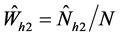: the estimated stratum weight among non-respondents.

: the sizes of the respondents.

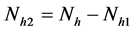: the sizes of non respondents groups.

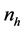: Units are drawn from the 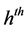stratum. Further let out of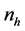, units belong to the respondents group.

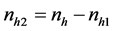: Units belong to the non respondents group.

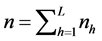: The total sample size.

A more careful second attempt is made to obtain information on a random subsample of size 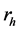out of 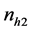non respondents for the representation from the non respondents group of the sample.

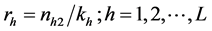: Subsamples of sizes at the second attempt to be drawn from 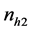non-respondent group of the stratum. Where and 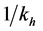denote the sampling fraction among non respondents. Since 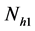and 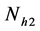are random variables hence their unbiased estimates are given as:

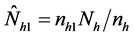: The unbiased estimates of the respondents group.

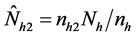: The unbiased estimate of the non respondents group.

: denotes the sample means of 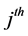characteristic measured on the 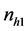respondents at the first attempt.

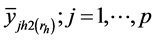: denotes the sub sampled units from non respondents at the second attempt.

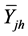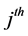Using the estimator of Hansen and Hurwitz [3] , the stratum mean for characteristic in the 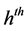stratum may be estimated by

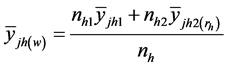(1)

It can be seen that 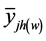is an unbiased estimate of the stratum mean 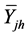of the stratum for the 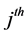characteristic with a variance.

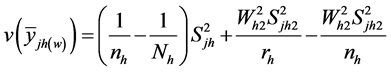(2)

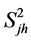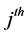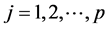where is the stratum variance of characteristic in the stratum; and 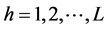given as:

where 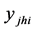denote the value of the 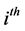unit of the 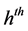stratum for 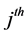characteristic.

: is the stratum mean of.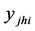

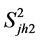is the stratum variance of the 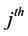characteristic in the 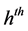stratum among non respondents, given by:

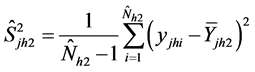
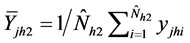is the stratum mean of among non respondents.

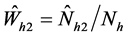is stratum weight of non respondents in stratum.

If the true values of 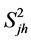and 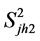are not known they can be estimated through a preliminary sample or the value of some previous occasion, if available, may be used.

Furthermore, the variance of 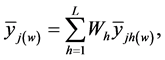(ignoring fpc) is given as:

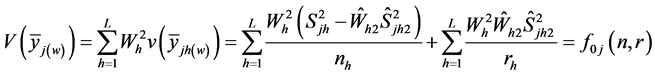(3)

where 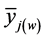is an unbiased estimate of the overall population mean 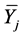of the characteristic and 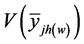is as given in Equation (2).

Assuming a linear cost function the total cost C of the sample survey may be given as:

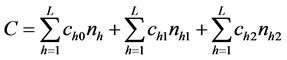
where 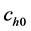= the per unit cost of making the first attempt, 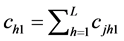is the per unit cost for processing the results of all the p characteristics on the 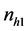selected units from respondents group in the 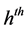stratum in the first attempt and 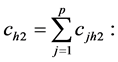the per unit cost for measuring and processing the results of all the p characteristics on the 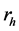units selected from the non respondents group in the 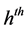stratum in the second attempt. Also, and 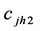are per unit costs of measuring the 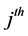characteristic in first and second attempts respectively. As 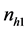is not known until the first attempt has been made, the quantity may be used as its expected value. The total expected cost 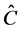of the survey may be given as:

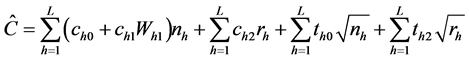(4)

The problem therefore reduces to find the optimal values of sample sizes of respondents 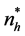and nonrespondents 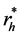which are expressed as:

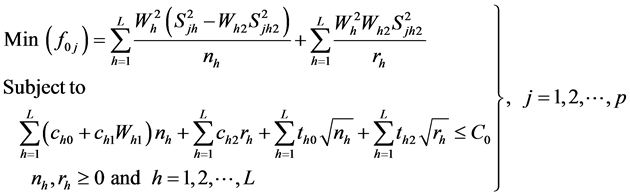(5)

3. Geometric Programming Formulation

The following Multi-objective Nonlinear Programming Problem (MNLPP) with the cost function quadratic in 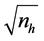and significant travel cost is defined in Equations (6) as follows:

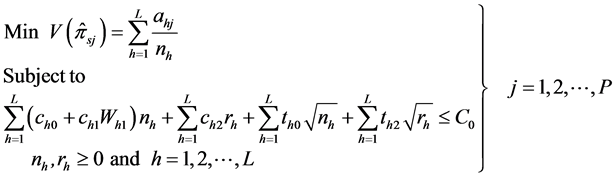(6)

Similarly, the expression (6) can be expressed in the standard Primal GPP with cost function quadratic in 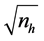where the travel cost is significant is given as follows:

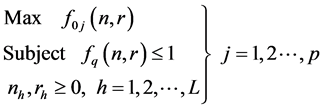(7)

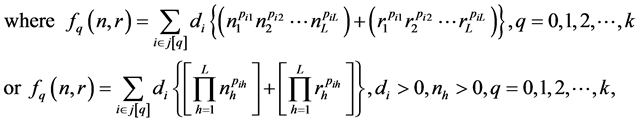
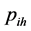: arbitrary real numbers,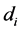: positive and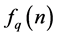: posinomials Let for simplicity 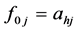and

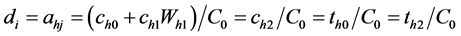
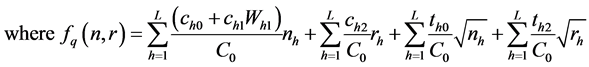
The dual form of the Primal GPP which is stated in (7) can be given as:

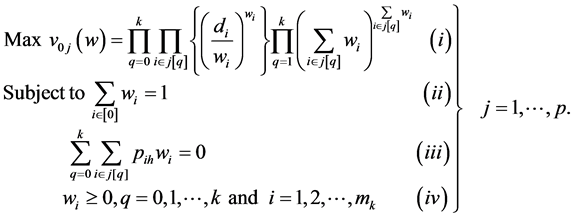(8)

The above formulated dual GPP (8) can be solved in the following two steps:

Step 1: For the Optimum value of the objective function, the objective function always takes the form:

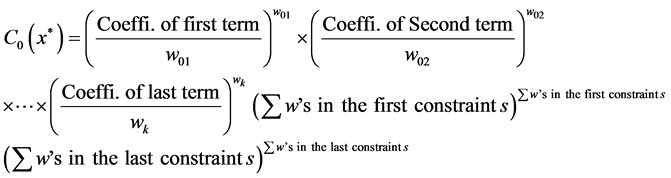
The Multi-Objective objective function for our problem is:

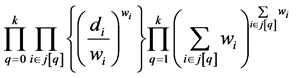
Step 2: The equations that can be used for GPP for the weights are given below:

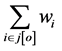in the objective function = 1 (Normality condition ) and for each primal variable 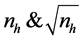and 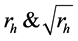having m terms.

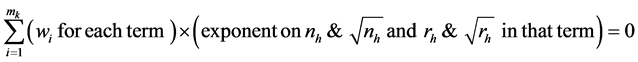(Orthogonality condition) and (Positivity condition).

The above problem (8) has been solved with the help of steps (1-2) discussed in Section (3) and the corresponding solutions 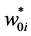is the unique solution to the dual constraints; it will also maximize the objective function for the dual problem. Next, the solution of the primal problem will be obtained using primal-dual relationship theorem which is given below.

4. Primal-Dual Relationship Theorem

If is a maximizing point for dual problem (8), each minimizing points 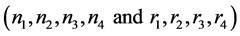for primal problem (7) satisfies the system of equations:

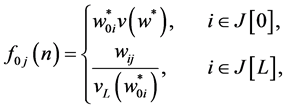(9)

where L ranges over all positive integers for which.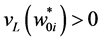

The optimal values of sample sizes of the respondents 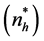and non-respondents 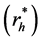can be calculated with the help of the primal-dual relationship theorem (9).

5. Fuzzy Geometric Programming Approach

The solution procedure to solve the problem (15) consists of the following steps:

Step-1: Solve the MOGPP as a single objective problem using only one objective at a time and ignoring the others. These solutions are known as ideal solution.

Step-2: From the results of step-1, determine the corresponding values for every objective at each solution derived. Let 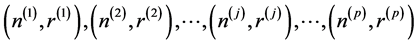are the ideal solutions of the objective functions

.

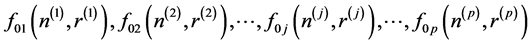So 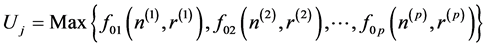and.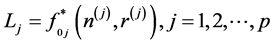

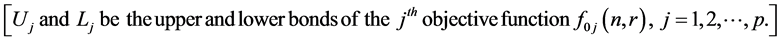
Step 3: The membership function for the given problem can be define as:

(10)

Here 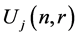is a strictly monotonic decreasing function with respect to.

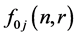The membership functions in Equation (11)

i.e.,

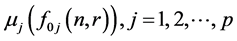
Therefore the general aggregation function can be defined as

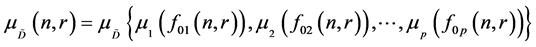
The fuzzy multi-objective formulation of the problem can be defined as:

(11)

The problem to find the optimal values of 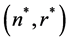for this convex-fuzzy decision based on addition operator (like Tiwari et. al. [29] ). Therefore the problem (11) is reduced according to max-addition operator as:

(12)

The above problem (12) reduces to

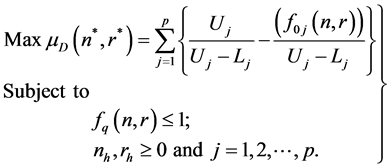(13)

The problem (13) maximizes if the function 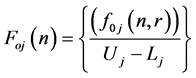attain the minimum values. Therefore the problem (13) reduces into the primal problem (14) define as:

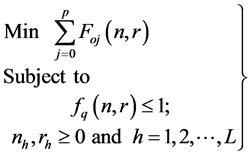(14)

The dual form of the Primal GPP which is stated in (16) can be given as:

(15)

The optimal values of sample sizes of the respondents 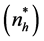and non-respondents 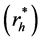can be calculated with the help of the primal-dual relationship theorem (9).

6. Numerical

In Table 1, the stratum sizes, stratum weights, stratum standard deviations, measurement costs and the travel costs within the stratum are given for two characteristics under study in a population stratified in four strata. The data are mainly from Khan et al. [8] . The travelling costs 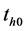and are assumed.

The total budget available for the survey is taken as The relative values of the variances of the non-respondents and respondents, that is 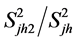is assumed to be constant and equal to 0.25 for j = 1,2 and h = 1,2,3,4. However, these ratios may vary from stratum to stratum and from characteristic to characteristic and can be handled accordingly.

For solving MOGPP by using fuzzy programming, we shall first solve the two sub-problems:

Sub problem 1: On substituting the table values in sub-problem 1, we have obtained the expressions given below:

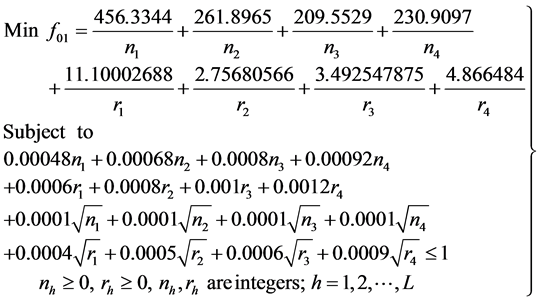(16)

The dual of the above problem (16) is obtained as:

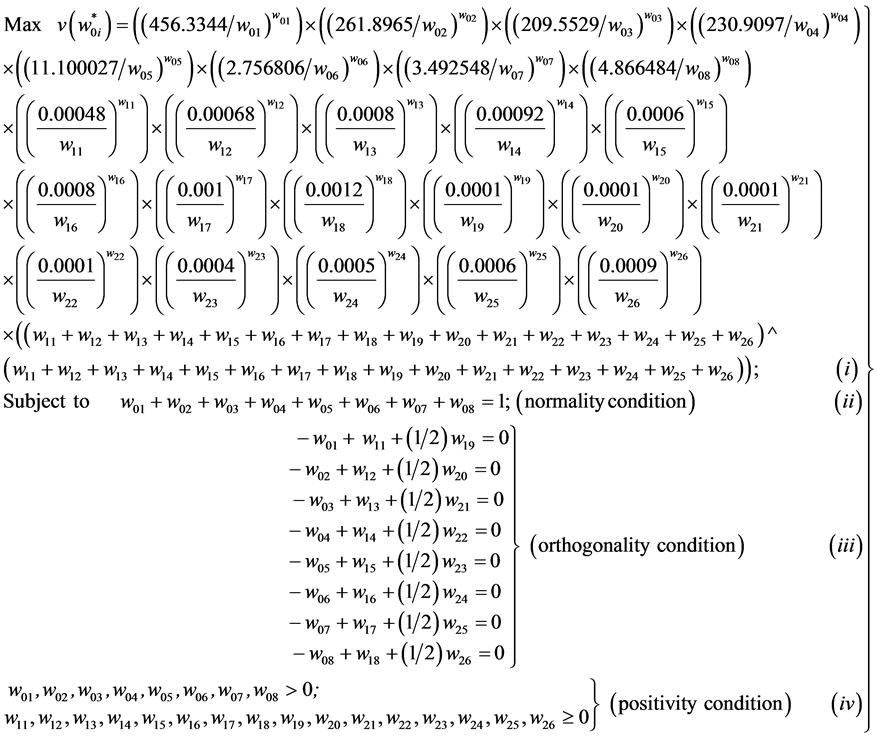(17)

For orthogonality condition defined in expression 17(iii) are evaluated with the help of the payoff matrix which is defined below

Solving the above formulated dual problem (17) with the help of Lingo software, we have the corresponding dual solutions as follows:

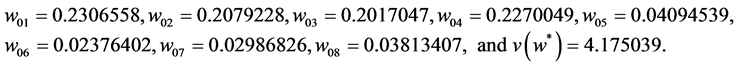
Using the primal dual-relationship theorem (9), we have the optimal solution of primal problem: i.e., the optimal sample sizes of respondents and non respondents are computed as follows:

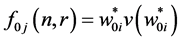
In expression (16), we first keep the r constant and calculate the values of n as:

Now, from the expression (16), we keep the n constant and calculate the values of r as:

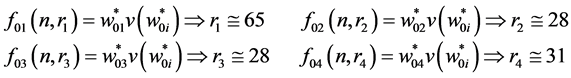
The optimal values and the objective function value are given below:

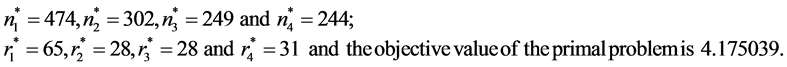
Sub problem 2: On substituting the table values in sub-problem 2, we have obtained the expressions given below:

(18)

The dual of the above problem (18) is obtained as follows:

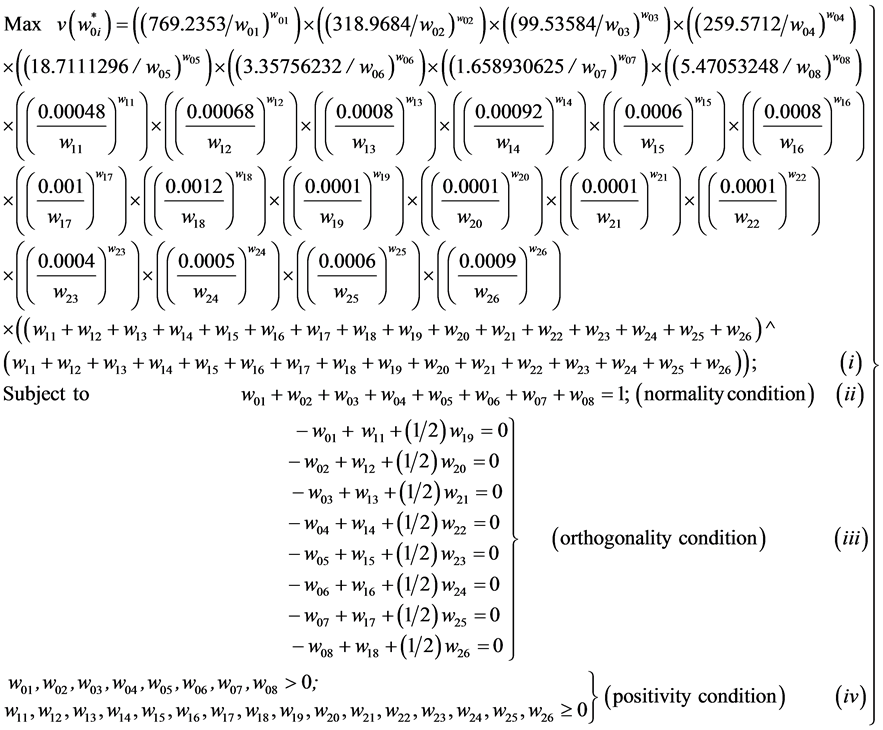(19)

For orthogonality condition defined in expression 19(iii) are evaluated with the help of the payoff matrix which is defined below:

Solving the above formulated dual problems, we have the corresponding solution as:

The optimal values of sample sizes of respondents and non-respondents can be calculated with the help of the primal-dual relationship theorem (9) as we have calculated in the sub-problem 1 are given as follows:

Now the pay-off matrix of the above problems is given below:

The lower and upper bond of can be obtained from the pay-off matrix

Let be the fuzzy membership function of the objective function and respectively and they are defined as:

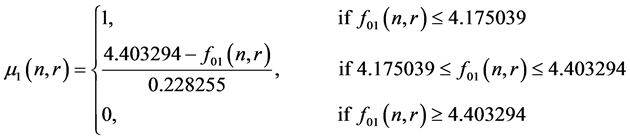
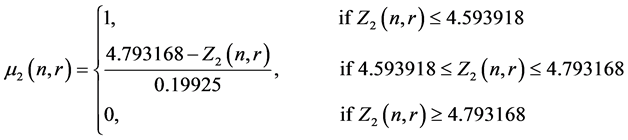
On applying the max-addition operator, the MOGPP, the standard primal problem reduces to the problem as:

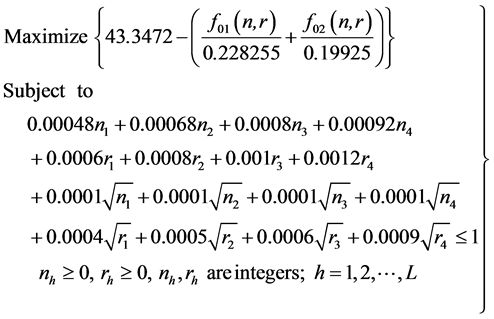(20)

In order to maximize the above problem, we have to minimize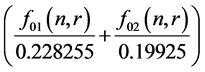, subject to the constraints as described below:

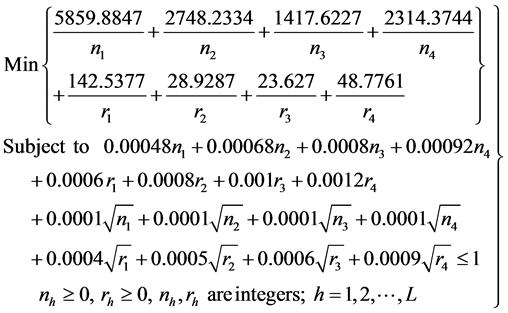(21)

Degree of Difficulty of the problem (21) is = (24 ‒ (8 + 1) =15.

Hence the dual problem of the above final formulated problem (21) is given as:

(22)

For orthogonality condition defined in expression 22(iii) are evaluated with the help of the payoff matrix which is defined below:

After solving the formulated dual problem (22) using lingo software we obtain the following values of the dual variables which are given as:

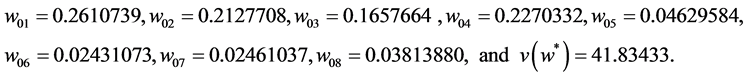
The optimal values of sample sizes of respondents and non-respondent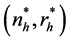s can be calculated with the help of the primal-dual relationship theorem (9) as we have calculated in the sub-problem 1 are given as follows:

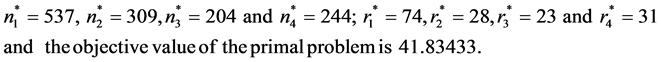
7. Conclusion

This paper provides an insightful study of fuzzy programming for solving the multi-objective geometric programming problem (MOGPP). The problem of non-response with significant travel costs where the cost is quadratic in in multivariate stratified sample surveys has been formulated of as a Multi-Objective Geometric Programming Problem (MOGPP). The fuzzy programming approach has described for solving the formulated MOGPP. The formulated MOGPP has been solved with the help of LINGO Software [30] and the dual solution is obtained. The optimum allocations of sample sizes of respondents and non respondents are obtained with the help of dual solutions and primal-dual relationship theorem. To ascertain the practical utility of the proposed method in sample surveys problem in presence of non-response with significant travel cost where the cost is quadratic in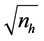, a numerical example is also given to illustrate the procedure.

References