American Journal of Operations Research
Vol. 3 No. 1A (2013) , Article ID: 27546 , 6 pages DOI:10.4236/ajor.2013.31A014
Research on Location Routing Problem (LRP) Based on Chaos Search (CS) and Empirical Analysis
1School of Economics and Finance, HuaQiao University, Quanzhou, China
2BPS Global Group, Hong Kong, China
Email: stu_zyl@yahoo.com.cn, shenzhongming88@126.com
Received November 21, 2012; revised December 22, 2012; accepted January 8, 2013
Keywords: Clustering Analysis; Chaos; Chaotic Behavior; Location Routing Problem (LRP);Logistics Distribution; Optimization; Regional Logistics
ABSTRACT
Due to the problem complexity, simultaneous solution methods are limited. A hybrid algorithm is emphatically proposed for LRP. First, the customers are classified by clustering analysis with preference-fitting rules. Second, a chaos search (CS) algorithm for the optimal routes of LRP scheduling is presented in this paper. For the ergodicity and randomness of chaotic sequence, this CS architecture makes it possible to search the solution space easily, thus producing optimal solutions without local optimization. A case study using computer simulation showed that the CS system is simple and effective, which achieves significant improvement compared to a recent LRP with nonlinear constrained optimization solution. Lastly the pratical anlysis is presented relationship with regional logistics and its development in Fujian province.
1. Introduction
All companies that aim to be competitive on the market have to pay attention to their organization related to the entire supply chain. In particular, companies have to increase the efficiency of their logistics operation. It is essential that reasonable optimal systems of logistics distribution for enterprises with the development of e-commerce and integrated logistics. Location-routing problem (LRP) is an important branch of routing optimization in integrated logistics systems, which has been solving for every logistics distribution corporations.
The conceptual foundation of LRP studies dates back to Von Boventer (1961), Maranzana (1965), Webb (1968), Lawrence and Pengilly (1969), Christofids and Eilon (1969) and Higgins (1972) [1]. Although these earlier studies are far from capturing the total complexity of LRP, they first recognized the close interface between location and transportation decisions. Watson-Gandy and Dohrn(1973)may be some of the first authors credited to consider the multiple-drop nature of the vehicle routes within the location-transportation framework [2]. Many scholars have developed more efficient problem solving techniques using the concept of integrated logistic systems, which include optimal models and their algorithms. Due to its complexity, it is models and algorithms that are core for solving LRP, which is NP-hard. More and more scientists have been interested in these works. Exact algorithms and heuristics are given in some articles. Exact algorithms for LRP can be classified into four categories: direct tree search (branch-and-bound), dynamic programing, integer programming, and non-linear programming. Heuristic includes location-allocation-first, route-second, route-first, and location-allocation-second, savings/insertion, and improve/exchange [3].
Chaotic system is a common phenomenon exiting in nonlinear dynamical system with popular characteristic of dynamics. Due to the ergodicity and randomness of chaotic sequence, the chaos search (CS) architecture can be solved the traditional optimization [4]. Much of engineering is concerned with the topic of optimization, and at the heart of much of the optimization are dynamical systems. Dynamical systems can be thought of either nonlinear continuous-time differential equation. Chaos occurs in dynamical systems, and frequently in engineering, which becomes the central fascination. Some of domestic scholars use chaos search for nonlinear optimization with constraints. The main advantage is to search the solution in certain field regardless of the continuous and difference of the function that can be solved complex optimization with constrains. Furthermore, it is easy to seek the optimal solutions (or near optimal solutions) without local optimization.
The main contribution of the paper is statement of a new hybrid algorithm combined clustering analysis and chaos search, together with a proof of their correctness [5]. Several clusters are divided by preference-fitting rules. Then the optimal route has been found using chaos in every cluster [6]. The simulation results show that it is an effective method. The paper is organized as follows.
Section 2 introduces the meaning and descriptions of LRP and describes the mathematical model of LRP. Section 3 emphasizes on the hybrid algorithm based on clustering analysis and chaos search for LRP. Section 4 shows the computational results and analysis. Finally, the last section gives conclusions and future work.
2. Description of LRP
Location-routing problem (LRP) is one of the problems in integrated logistics optimizations. The LRP can be defined as follows. A feasible set of potential facility sites and location; and expected demands of each customer are given. Each customer is to be assigned to a facility, which will supply its demand. The shipments of customer demand are carried out by vehicles, which are dispatched from the facilities and operated on routes that include multiple customers. There is a fixed cost associated with opening a facility at each potential site, and a distribution cost associated with any routing of vehicles that includes the cost of acquiring the vehicles used in the routing, and the cost of delivery operations. The cost of delivery operations is linear in the total distance traveled by the vehicles [7]. The LRP is used to determine the location of the facilities and the vehicle routes from the facilities to customers, with the aim of minimizing the sum of the location and distribution costs, while ensuring that the vehicle capacities are not exceeded [8]. The expression of LRP is given in Figure 1.
A constraint-based model is presented in this paper for the location routing problem. The hypotheses are as follows:
The transportation is just in time.
The facility is both starting point and destination of circular vehicle routing; each facility serves more than two customers.
Nature of demand/supply: deterministic.1 There are multiple facilities.
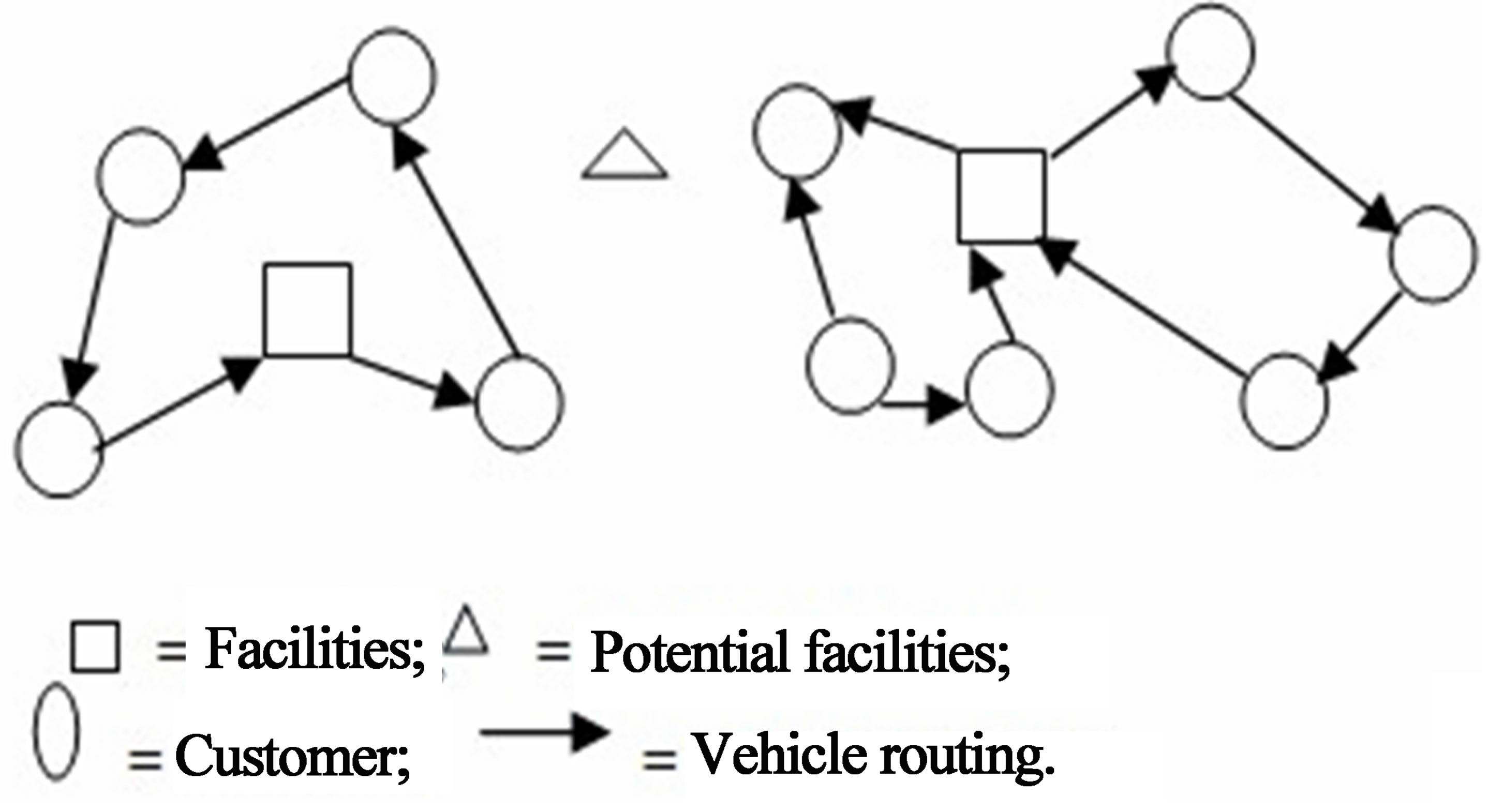
Figure 1. Expression of LRP.
Size of vehicle fleets: single vehicle (A facility is served by one vehicle; meanwhile, it is satisfied that the total demand of the route is no less than one vehicle’s capacity).
Vehicle capacities are determined. The total quantity (amount) of goods is limited in every route by each vehicle’s capability.
Facility capacities are undetermined; not all facilities have been chosen in every decision.
Each customer is served by one and only one vehicle. Considering the complexity of supply/demand markets, it is assumed that they are retail markets.
Each facility is considered a separate entity, not linked to the other facilities.
Objective: minimize total costs.
2.1. Decision Variables Considered Are as Follows

2.2. Model Parameters Are Given as Follows
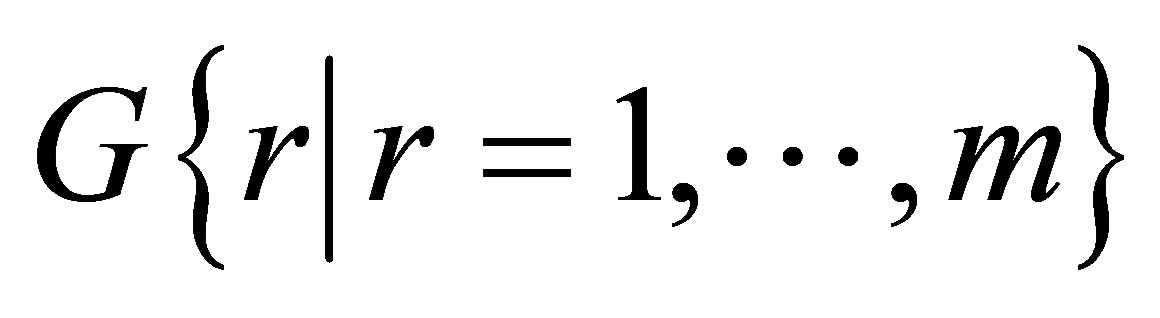
is the set of m feasible sites of candidate facility,

is the set of N customers to be served,

is the set of all feasible sites and customers (it is also referred to nodes),
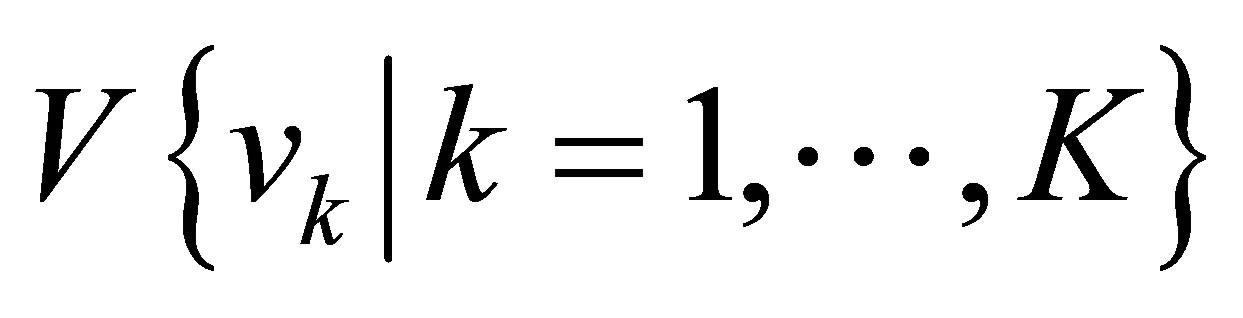
is the set of K vehicles available for routing from the facilities, 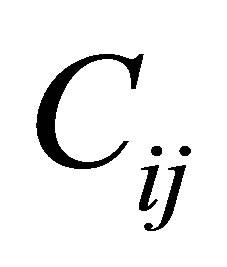 average annual cost per distance traveling from
average annual cost per distance traveling from
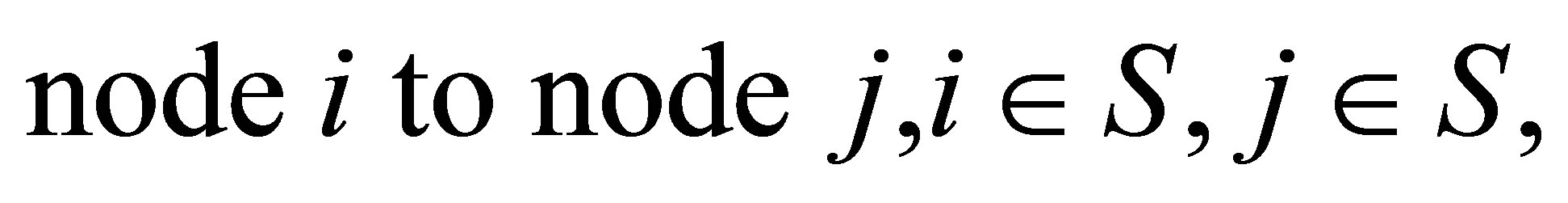
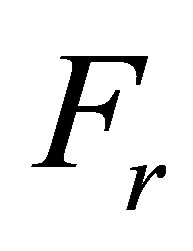 annual cost of establishing and operating a facility at site
annual cost of establishing and operating a facility at site ,
, 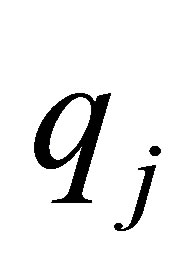 average number of units demands by customer
average number of units demands by customer 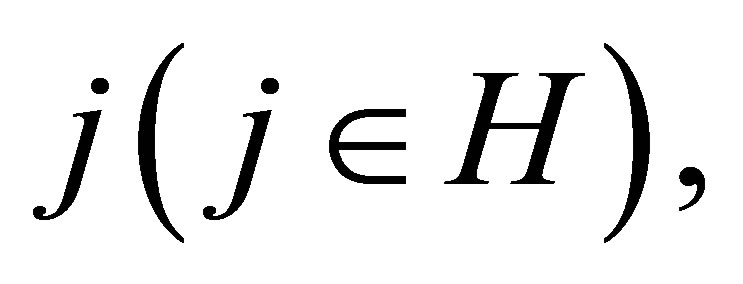
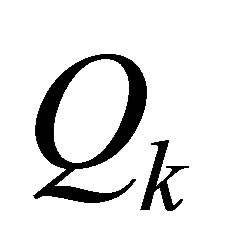 capacity of vehicle
capacity of vehicle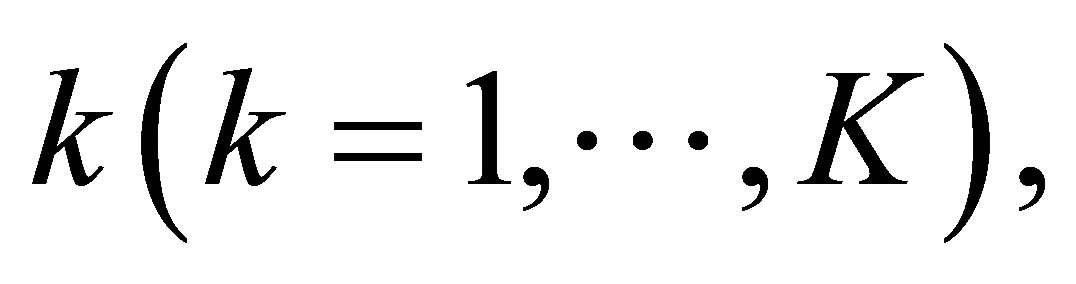
 distance from node i to node j,
distance from node i to node j, 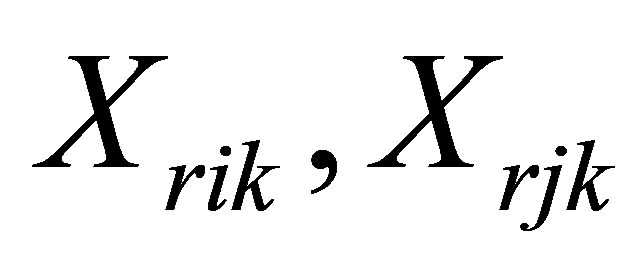 traveling by vehicle k from node r to customer i or to customer j, respectively.
traveling by vehicle k from node r to customer i or to customer j, respectively.
2.3. Model of a Special LRP Is Defined as Follows
The objective function of LRP is
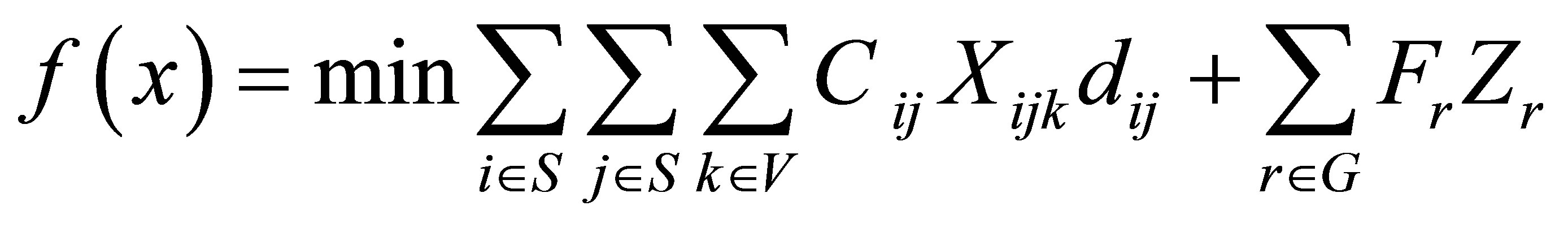 (1)
(1)
Subject to
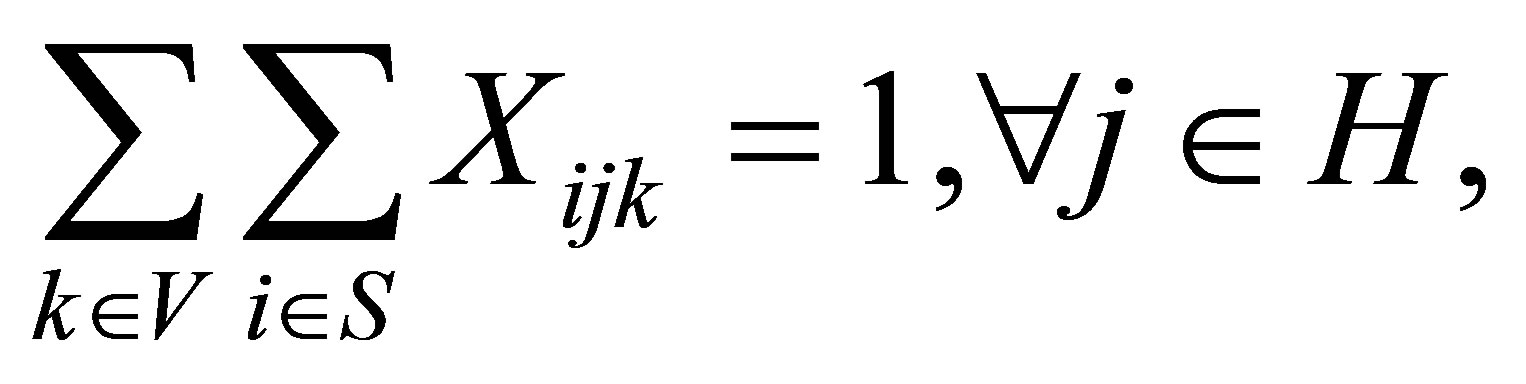 (2)
(2)
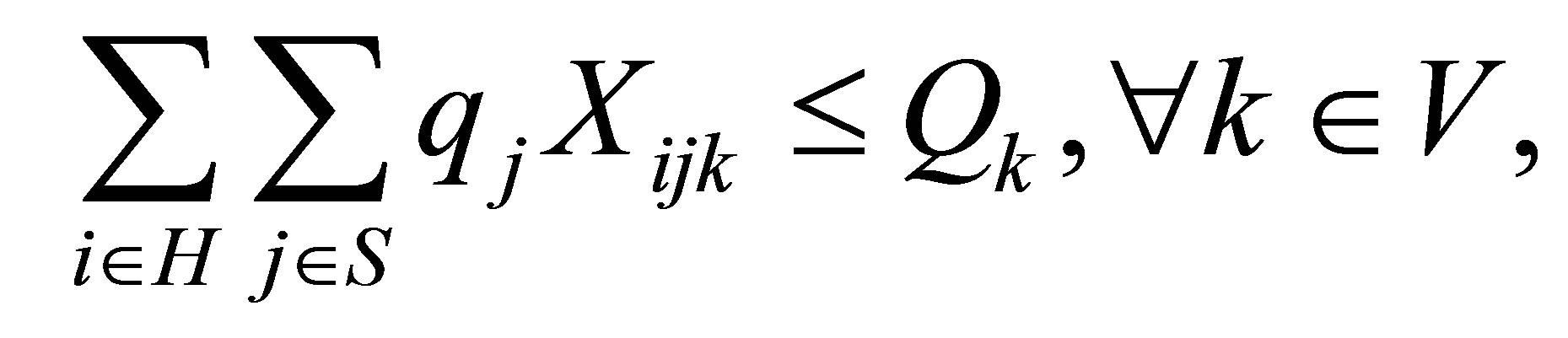 (3)
(3)
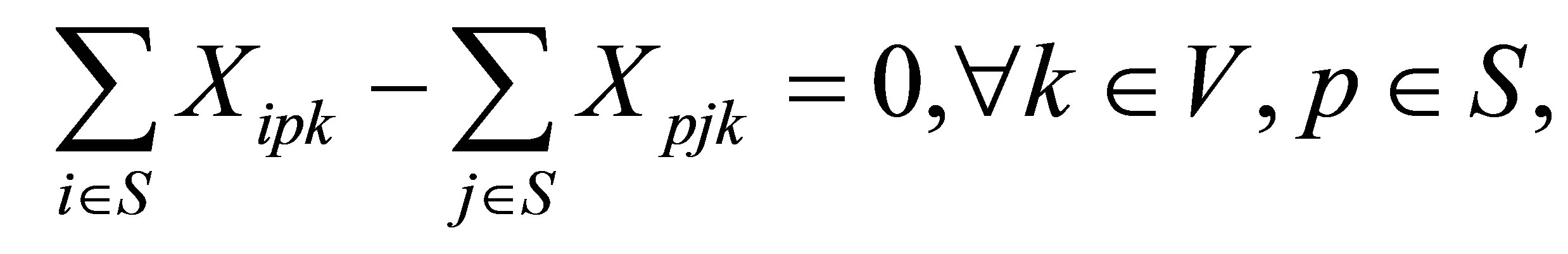 (4)
(4)
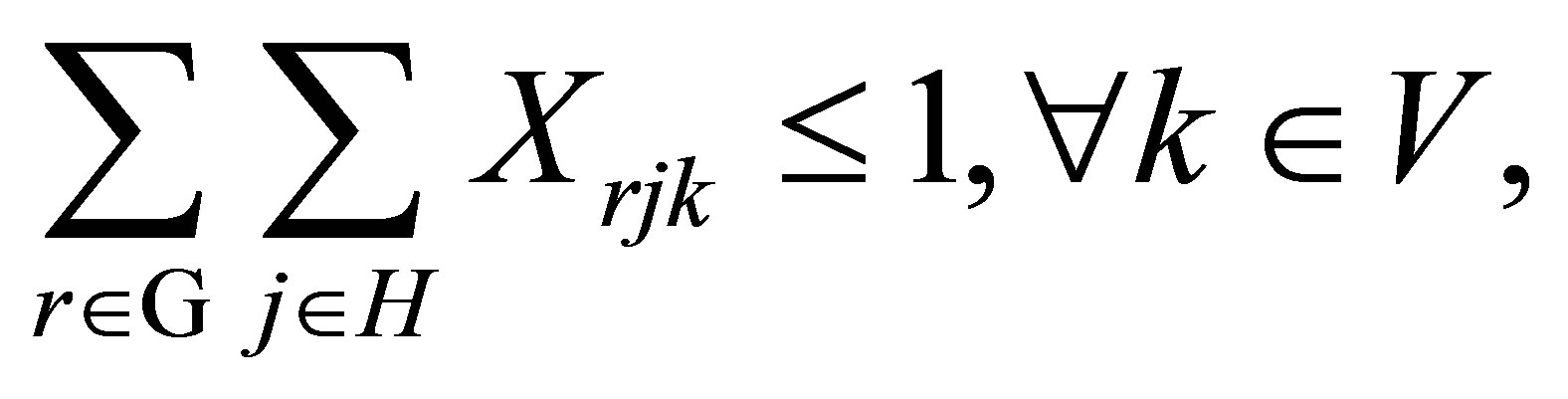 (5)
(5)
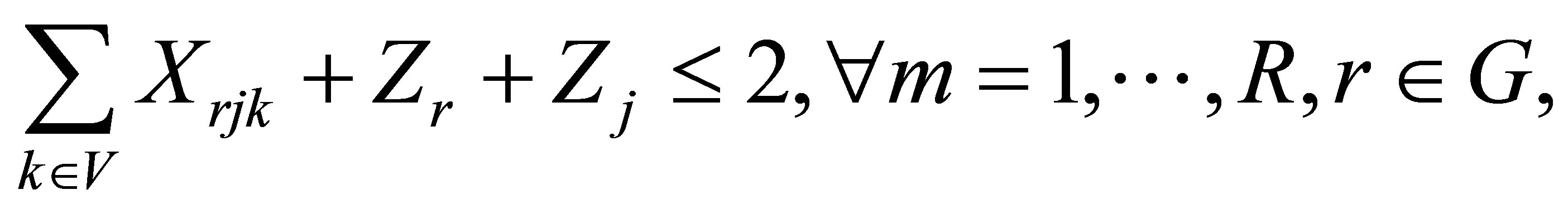 (6)
(6)
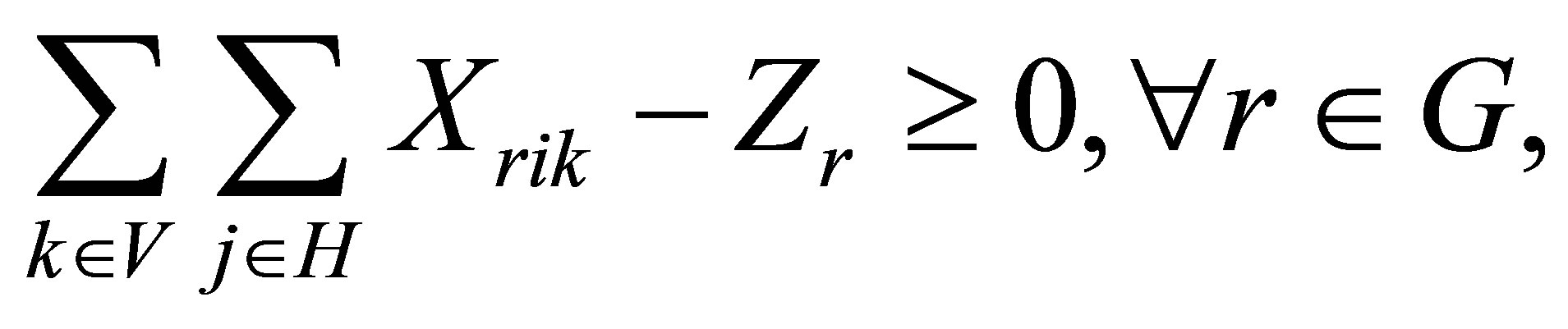 (7)
(7)
 (8)
(8)
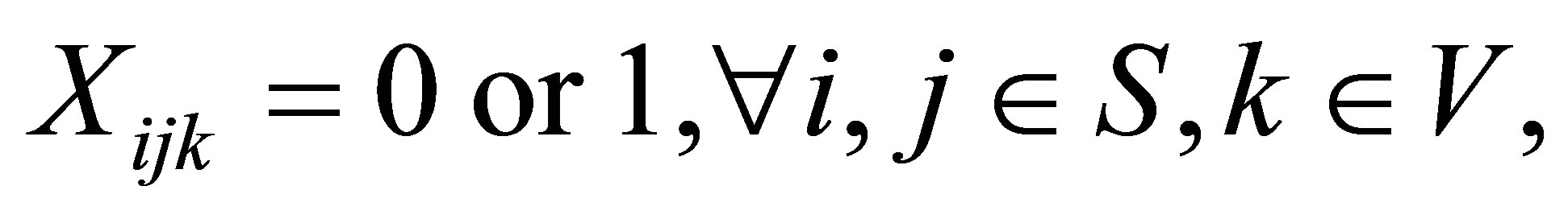 (9)
(9)
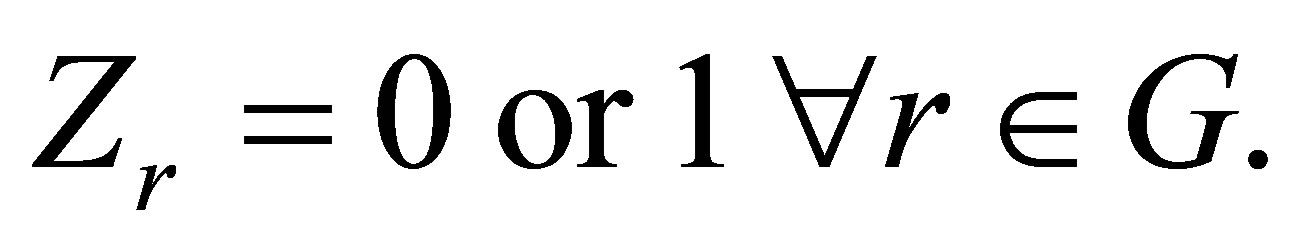 (10)
(10)
In this model, the objective function minimizes the total cost of routing, and establishing and operating the facilities. Constraint (2) ensures that each customer is served by one and only one vehicle. Constraint (3) ensures that the vehicle capacity constraints are not exceeded for any of the vehicles used in routing, while (4) is the route continuity constraint, which implies that the same vehicle should leave every point that is entered by a vehicle. Constraint (5) guarantees that each vehicle is routed from one depot. Constraint (6) guarantees that there are no links between any two depots. Constraints (7) and (8) require that a vehicle can only from a depot if that depot is opened. The last two of constraints are the integer constraints.
3. A Hybrid Algorithm Based on Clustering Analysis and Chaos Search for LRP
3.1. Clustering Analysis of LRP
Clustering analysis is one of the major techniques in pattern recognition. It is a technique for grouping data and finding where similar data are assigned to the same cluster whereas dissimilar data should belong to different clusters. The conventional clustering methods generate partitions, in a partition; each pattern belongs to one and only one cluster.
The customer aggregate C is divided to cluster by the euclidean measure. The steps of optimal facility location are performed in the following way, which have extensively analyzed and used in location theory to approximate distances between two spatial coordinates. For the sake of simplicity, it is assumed that each facility has its own set m of their coordinates of candidate sites for facility location, and no two facilities share the same location, which are denoted by
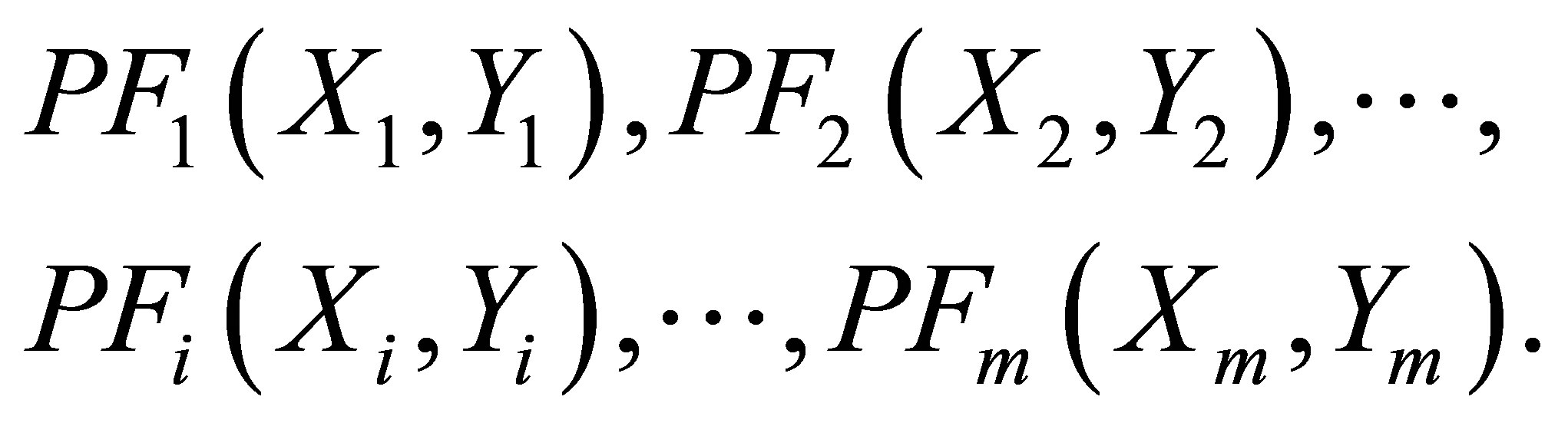
Every two coordinates of candidates sites for facility locations are denoted by 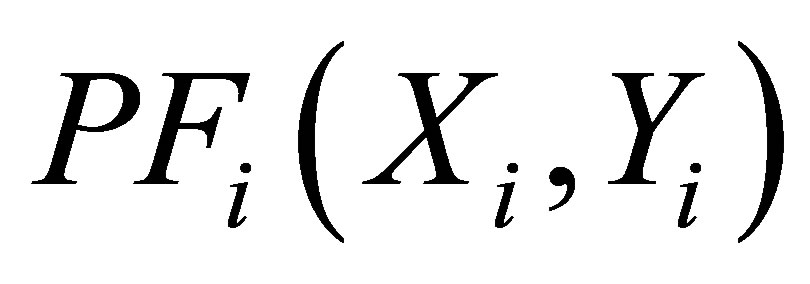 and
and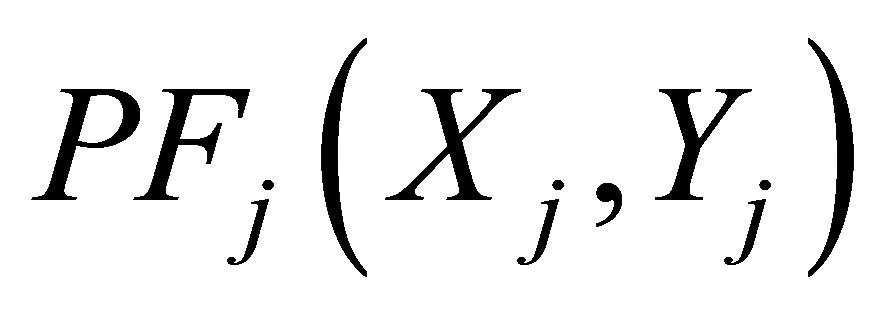 , and which satisfied with
, and which satisfied with
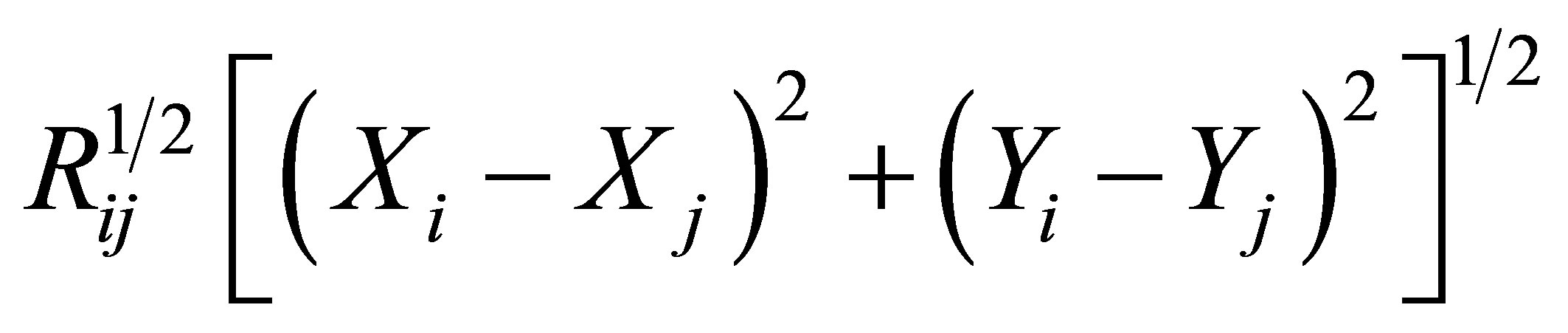 (11)
(11)
where Rij is one half of the distance between 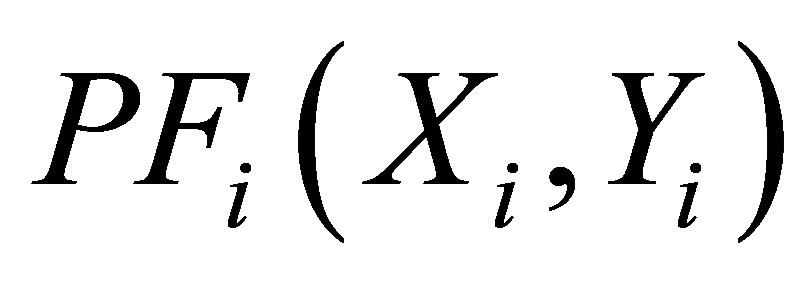 and
and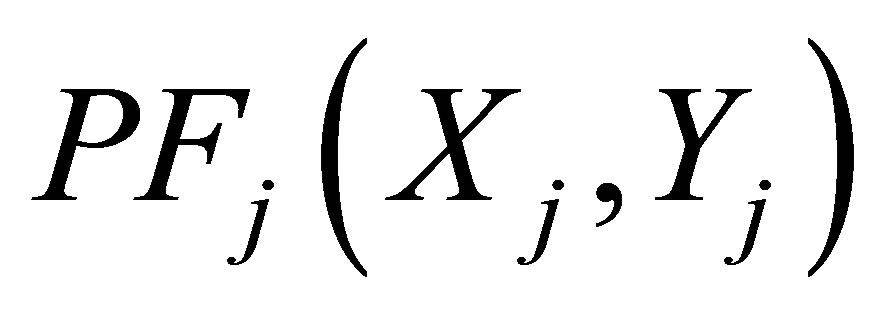 .
.
Rules for classification are given as follows.
Rule1 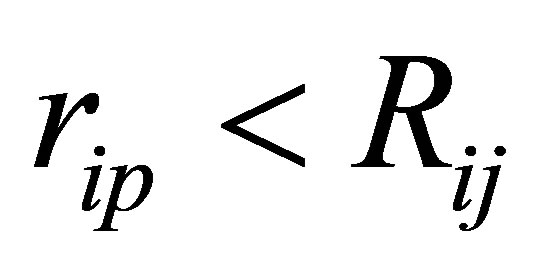 (12)
(12)
Cp can only be divided into PFi if formula (12) is true.
Rule 2 The coordinates of customers on the circumferences are satisfied that the distance to the nearest two customers is less than that to the sub nearest two points. sub-nearest meaning that they are not included a cluster by reason of distance).
Rule 3 If 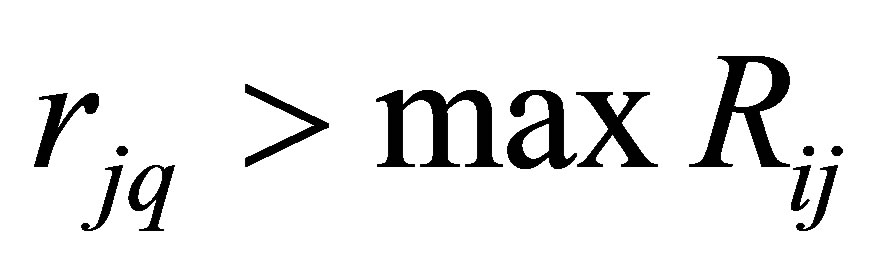 (13)
(13)
where rjq is the distance from any customer Cq to any facility PFj, maxRij is half of the most distance between any two facilities. Either these customers will not be served, or else the candidate’s facility location will be abolished. Last two rules only relate to abnormal customers points.
where N is the numbers of customers,
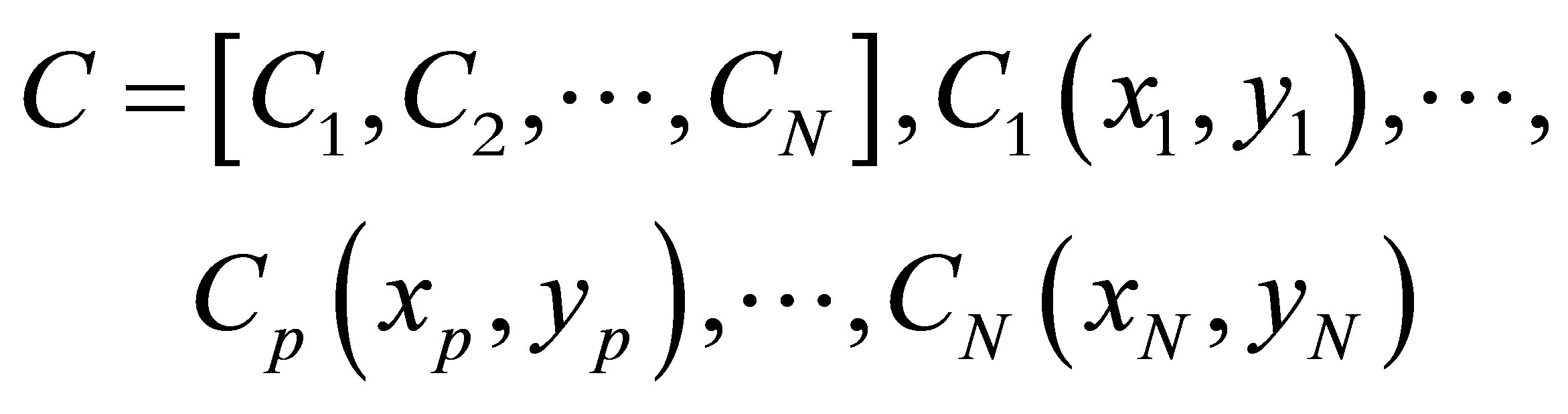
are expressed the points and their coordinates, respectively.
rip is the distance between any candidate facility PFi and any customer p. The tangent cycles O1, O2, …, Oi, Oj, …, Om are drawn with the radius Rij , where R1, R2, …, Ri, Rj, …, Rm are their radiuses, respectively.
3.2. An Algorithm of Chaos Search Optimization for LRP
The fundamental idea is that chaotic sequences belonging to the ergodic points in [0,1] are constructed by the chaos system [9]. They transform to chaotic ergodic variables in solution space of optimization and then search for a good solution. Chaotic sequences are produced by the chaotic equation, of which the Logistic difference equation is one of the most typical models [10]. The Logistic difference equation is defined as.
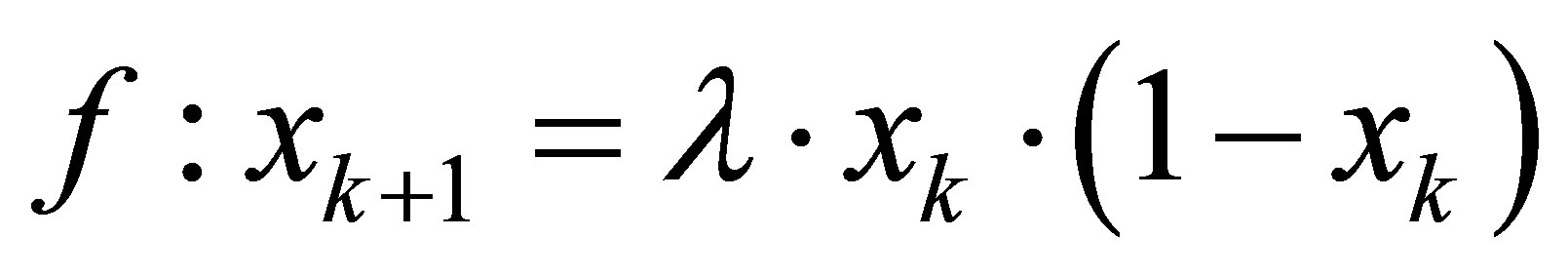 (14)
(14)
where ![]() is the so called driving parameter(a parameter capturing such factors as fertility rate) initial living area, etc. The initial value, or seed x is in
is the so called driving parameter(a parameter capturing such factors as fertility rate) initial living area, etc. The initial value, or seed x is in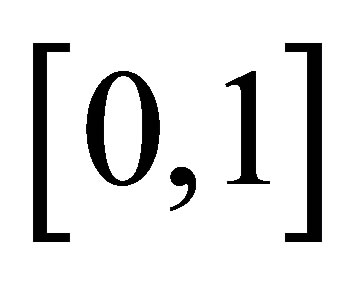 .
.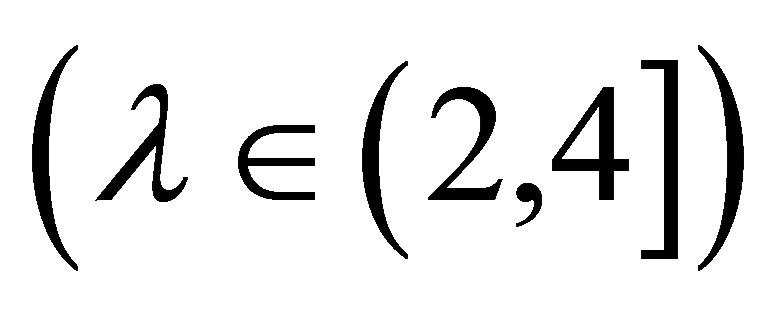 , There
, There 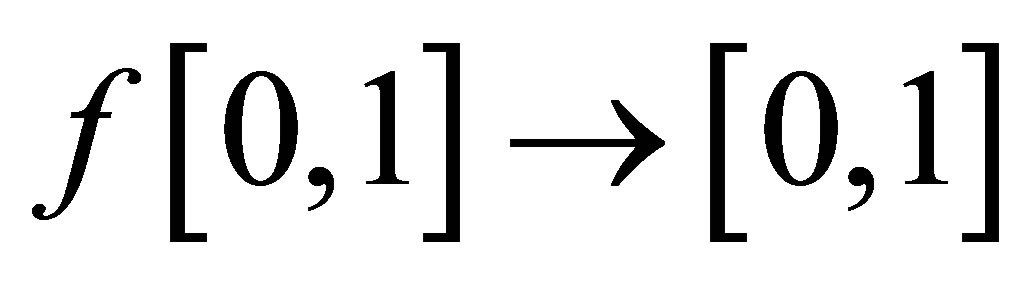 if
if 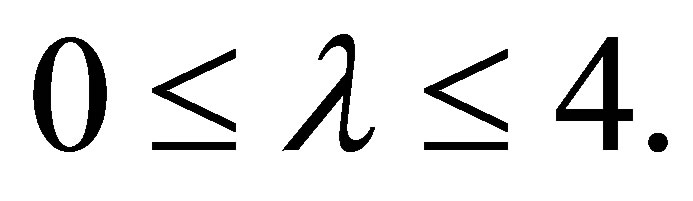 From about x is restricted to
From about x is restricted to 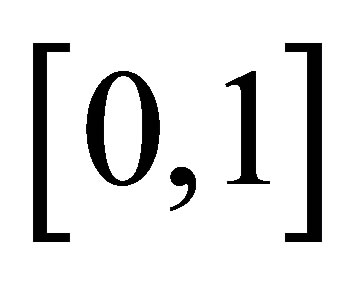 and
and![]() to
to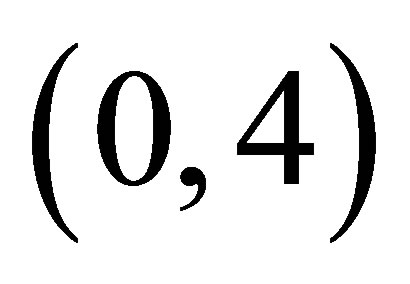 .
.
The characteristic of Logistic map is given as follow:
1) When λ to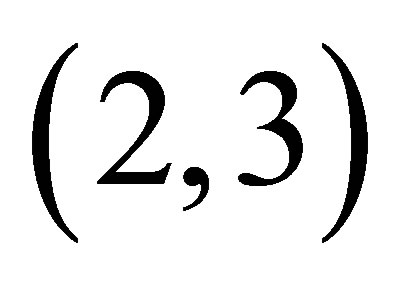 , there are stable points in Logistic map.
, there are stable points in Logistic map.
2) When λ to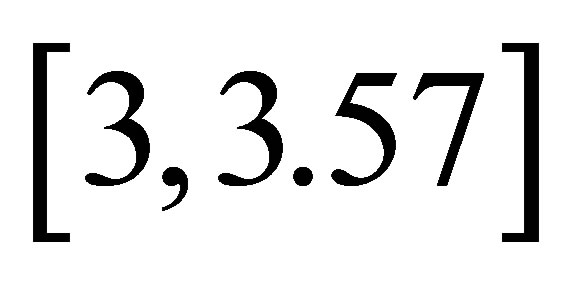 , two sequences with seeds only slightly apart diverge very rapidly, that is to say, there exists in the period-doubling bifurcation of the solutions.
, two sequences with seeds only slightly apart diverge very rapidly, that is to say, there exists in the period-doubling bifurcation of the solutions.
3) When λ to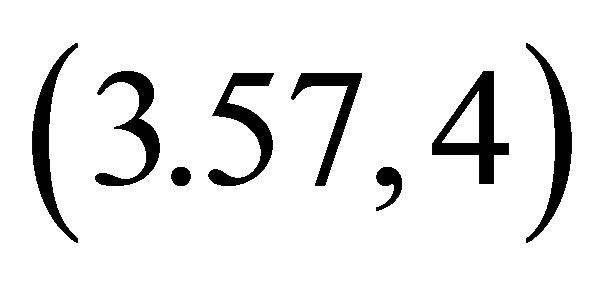 , chaos start to come out, and Logistic map isn’t in stable cycling orbit. It is difficult to decide which points with Lebesgueis more than zero in chaotic sequences.
, chaos start to come out, and Logistic map isn’t in stable cycling orbit. It is difficult to decide which points with Lebesgueis more than zero in chaotic sequences.
4) When λ to 4, there is a stable chaotic sequence.
In the stable chaotic sequence, any orbit f is dense, that is to say, the points of one orbit f is included in open ball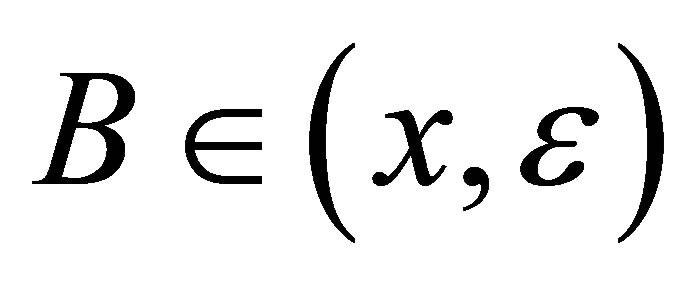 , when
, when 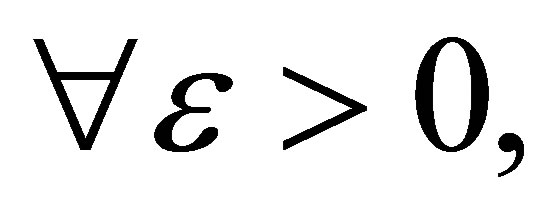 and
and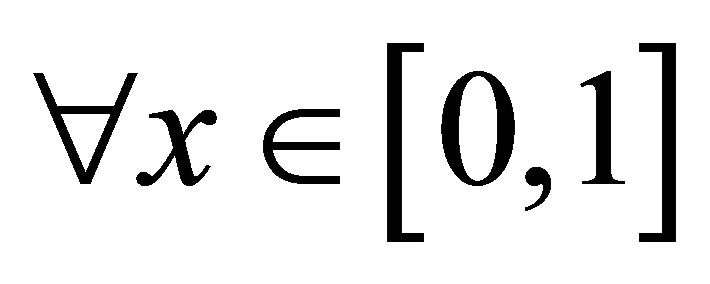 . On the contrary, all points that belong to
. On the contrary, all points that belong to 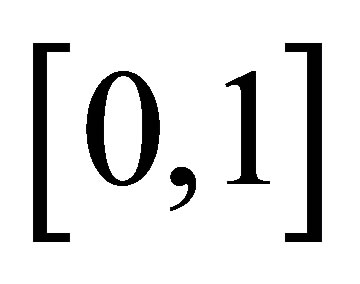 are pressed on towards any orbit f as precision as possible. In this paper when
are pressed on towards any orbit f as precision as possible. In this paper when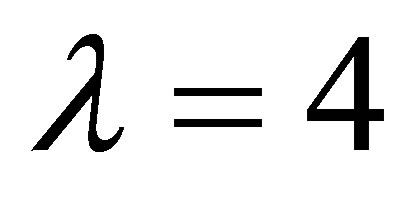 , the population sequence
, the population sequence 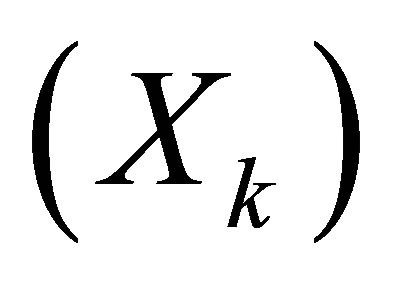 is chaotic and ergodic and gives search optimal solutions (or near optimal solutions) solutions. A chaotic system is defined as one where two different, but close, seeds result in widely different population sequences. An ergodic system is one where the sequences
is chaotic and ergodic and gives search optimal solutions (or near optimal solutions) solutions. A chaotic system is defined as one where two different, but close, seeds result in widely different population sequences. An ergodic system is one where the sequences 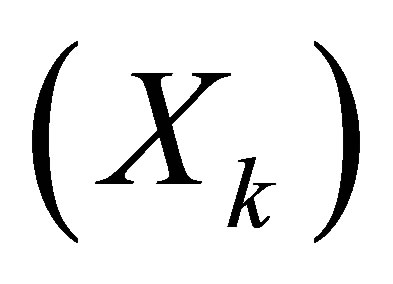 will approach every possible point arbitrarily, little by little (more formally, for every pair of element of
will approach every possible point arbitrarily, little by little (more formally, for every pair of element of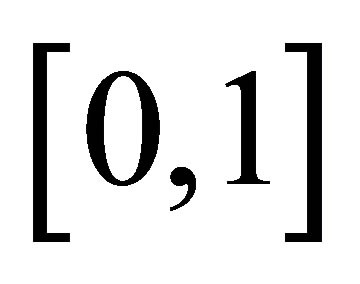 , there is an xk between them). Thus, an ergodic system is one that is “trying to converge to everything”. The Logistic model can be solved not only for the continuous variable optimization, but also discrete variable optimization.
, there is an xk between them). Thus, an ergodic system is one that is “trying to converge to everything”. The Logistic model can be solved not only for the continuous variable optimization, but also discrete variable optimization.
3.3. A Hybrid Algorithm for LRP
The hybrid algorithm includes two steps. First, preference-fitting rules to solve location-allocation cluster the customers. Second, the optimal routes is obtained by chaos search to be minimized the function. The Logistic chaotic model is transformed for discrete optimization of LRP [11]. A legal route will be determined with the numbers customer of r in one cluster, that is to say, the order of the customer clusters will be arranged [12]. The variable d indicates the route distance in any cluster to be minimized.
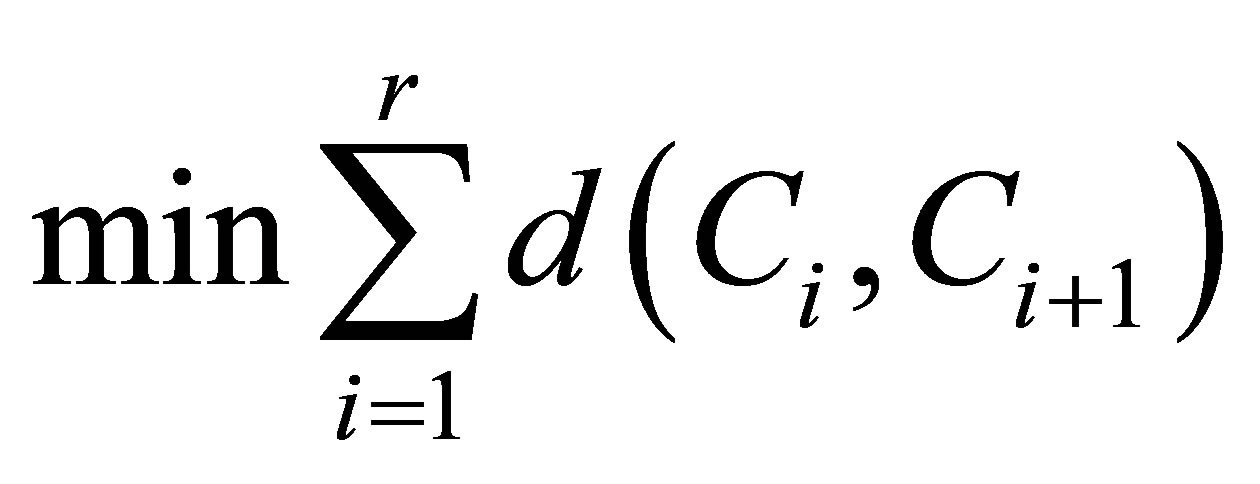 (15)
(15)
where
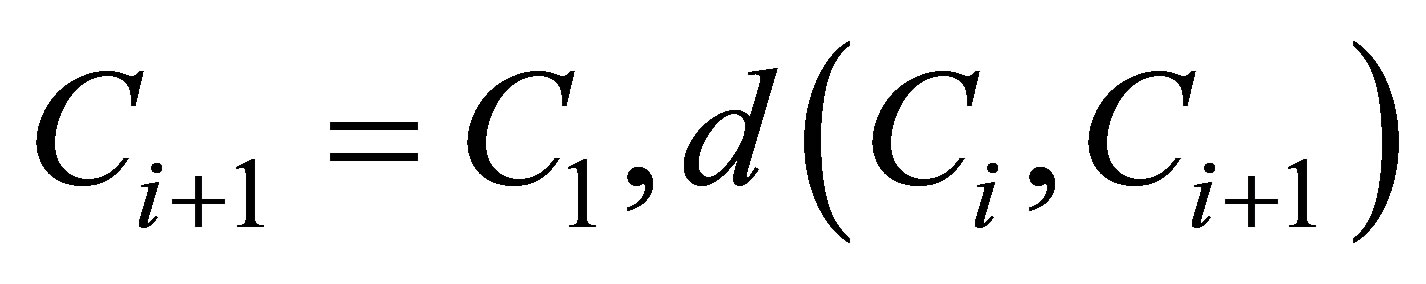 (16)
(16)
denoted the distance between customer  and customer
and customer .
.
Steps with the hybrid algorithm based on clustering analysis and chaos search are described as follow.
Step 1 Customers are clustered by preference-fitting rules.
1) Initial calculations for Rij and rip are performed.
2) If rip < Rij, the customer p is divided into cluster Oi.
3) Otherwise, return step (1.1).
Step 2 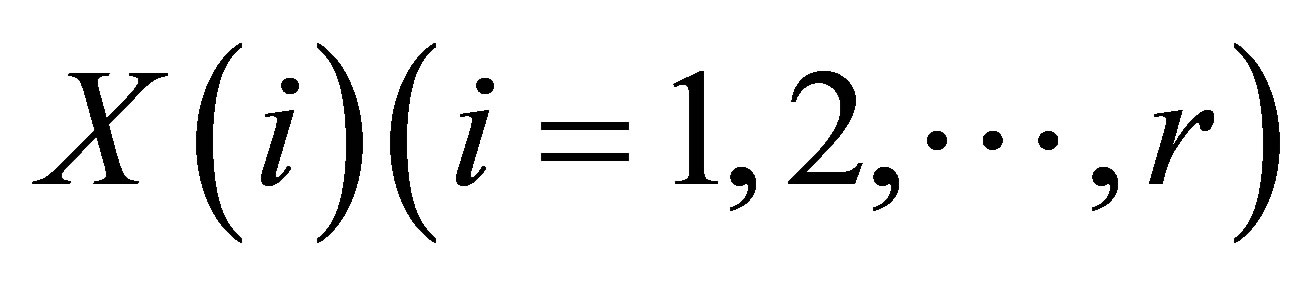 is given by initial random value. The best optimal value of the function
is given by initial random value. The best optimal value of the function , given with the control parameter k gifted with a larger value.
, given with the control parameter k gifted with a larger value.
Step 3 Put the results of order arranged 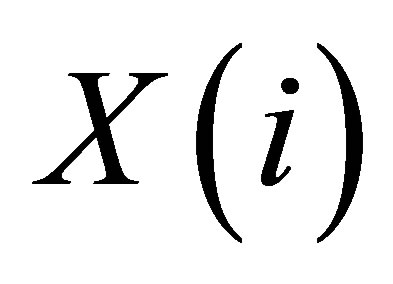 into
into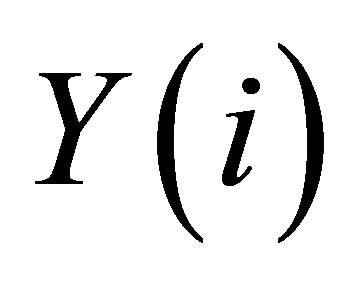 . It is obtainable to a current searching route, and to a current legal route by hybrid algorithm, compared with
. It is obtainable to a current searching route, and to a current legal route by hybrid algorithm, compared with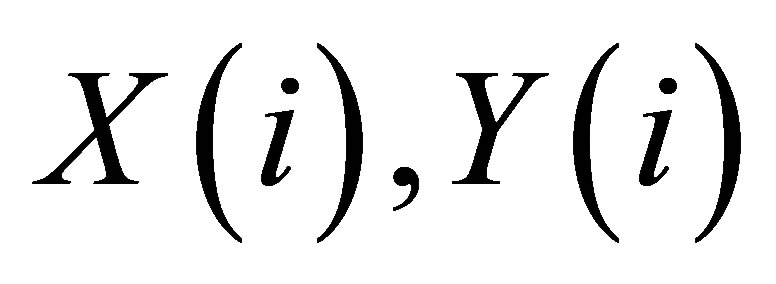 .
.
Step 4 Calculate the function values f of the current legal route.
Step 5 Remember the minimum function values 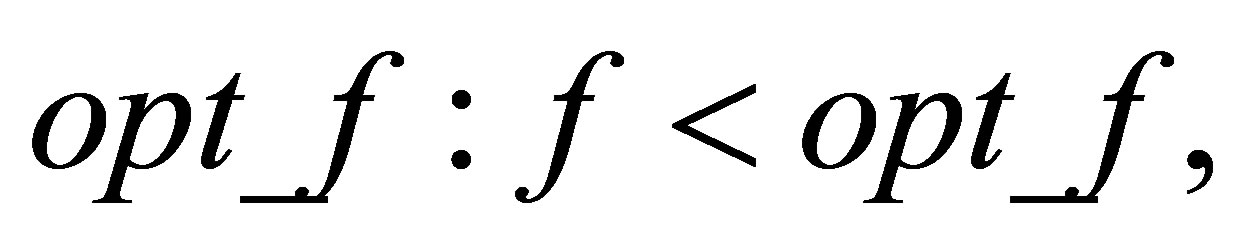 and
and 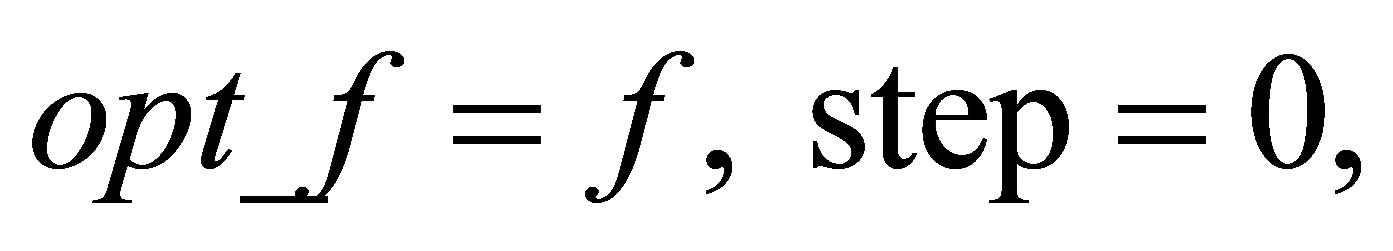 and also remembering the present legal route.
and also remembering the present legal route.
Step 6 Decide whether the cycle is stopped or not. If step = k, stop.
Step 7 A set of  is generated by Logistic map, step = step + 1.
is generated by Logistic map, step = step + 1.
Step 8 Return steps 3, and cycling.
4. Analysis of the Computational Results
In the following example three potential facilities, and ten customs were analyzed. Each was served. With the same type of distribution vehicle that had a carrying capacity equal to 30 ton. The annual cost establishing and operating a facility Fr is equal to 160 yuan/each, The transportation cost Cij is equal to 2 yuan per ton, per km. The hybrid algorithm has been discussed to search the optimal route based on the data in Table 1.The programming is edited by VC++. The results of clustering analysis and running by 50,000 times are given in Table 2.
The simulation results are shown in Table 2. As seen in this table, it is an effective method based on clustering analysis and chaos search proposed in this paper. This method can be sought optimal solution (or near optimal solutions) adaptively and quickly for many candidate facilities and customers. The computational cost is dramatically reduced by chaos search to solving the smallscale question. The proposed optimal algorithm provides a new path for large-scale optimization in practical integrated logistics
5. Empirical Analysis
The empirical analysis is given in relationship between with regional logistics and regional economy. The model
Table 1. Coordinate position of three potential facilities and ten customs.
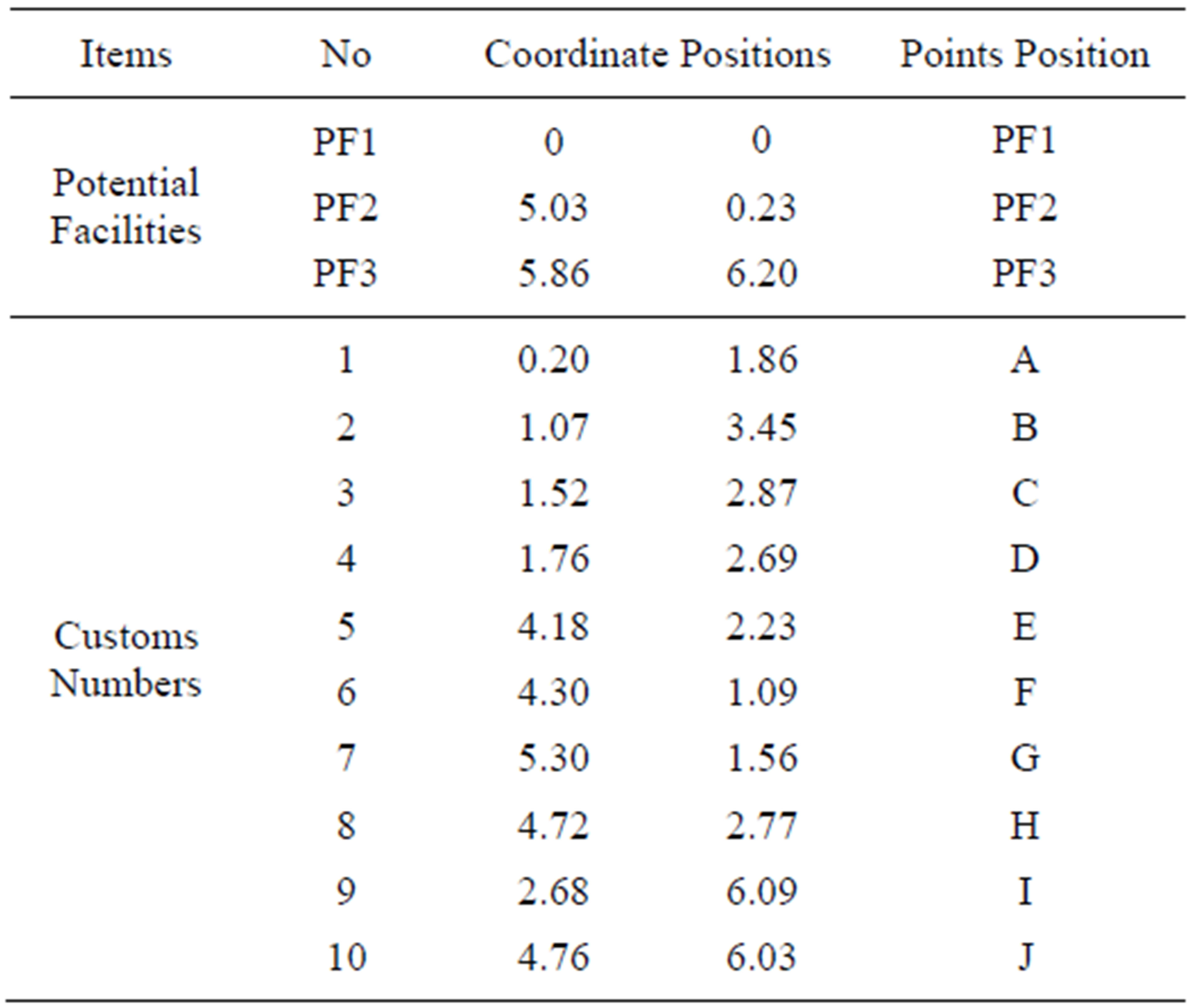
Table 2. Simulation results.

with analysis is proposed for the relationship with modern logistics and GDP. The factors are chosen include GDP, logistics production value (WLCZ), freight turnover (HZL), logistics mileage (WLC), and which the data is chosen from 1978 to 2010. The unchangeable price in1978 is given with each variable. The quantitative software is accepted with EVIEWS 6.0, and which the trend of each variable is give in Figure 2 including GDP, WLCZ, HZL, WLC.
5.1. Unit Root Test
Test type (C, T, K), The letters of C, T, K means intercept, Trend, lagging numbers. The first four are contains intercept and trend; The after four are not contains trend.
From the Table 3, it is known that the original data in time trend, after an order difference or second order difference, the data is smooth.
5.2. Co-integration Test
The Johansen co-integration test is accepted for GDP, WLCZ, HZL, WLC. This test results is presented in Table 4.
From Table 4, refused to no co-integration variables of the null hypothesis in 5% level of trace statistics.
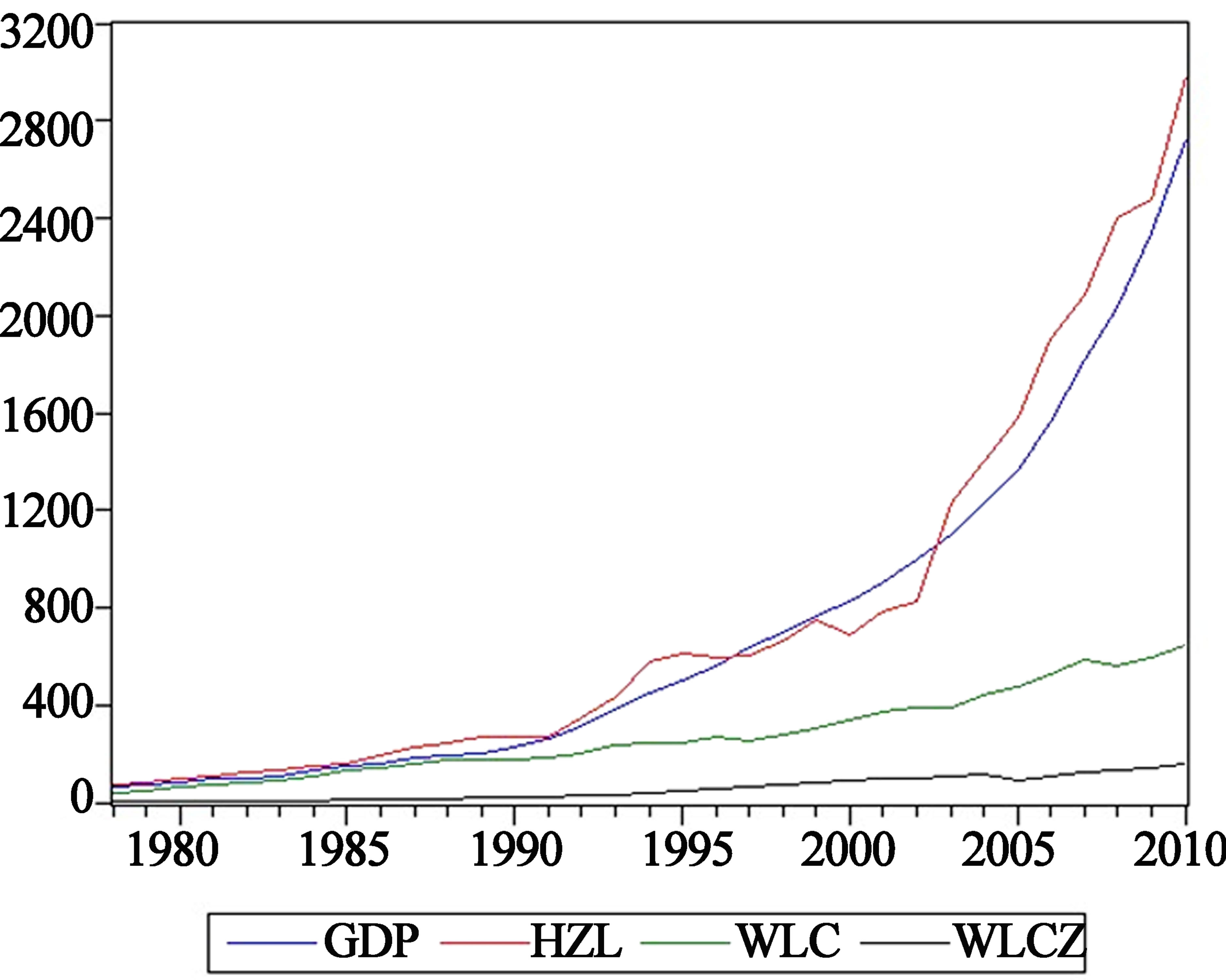
Figure 2. The trend of each variable.
Table 3. ADF unit root test results of each variable.
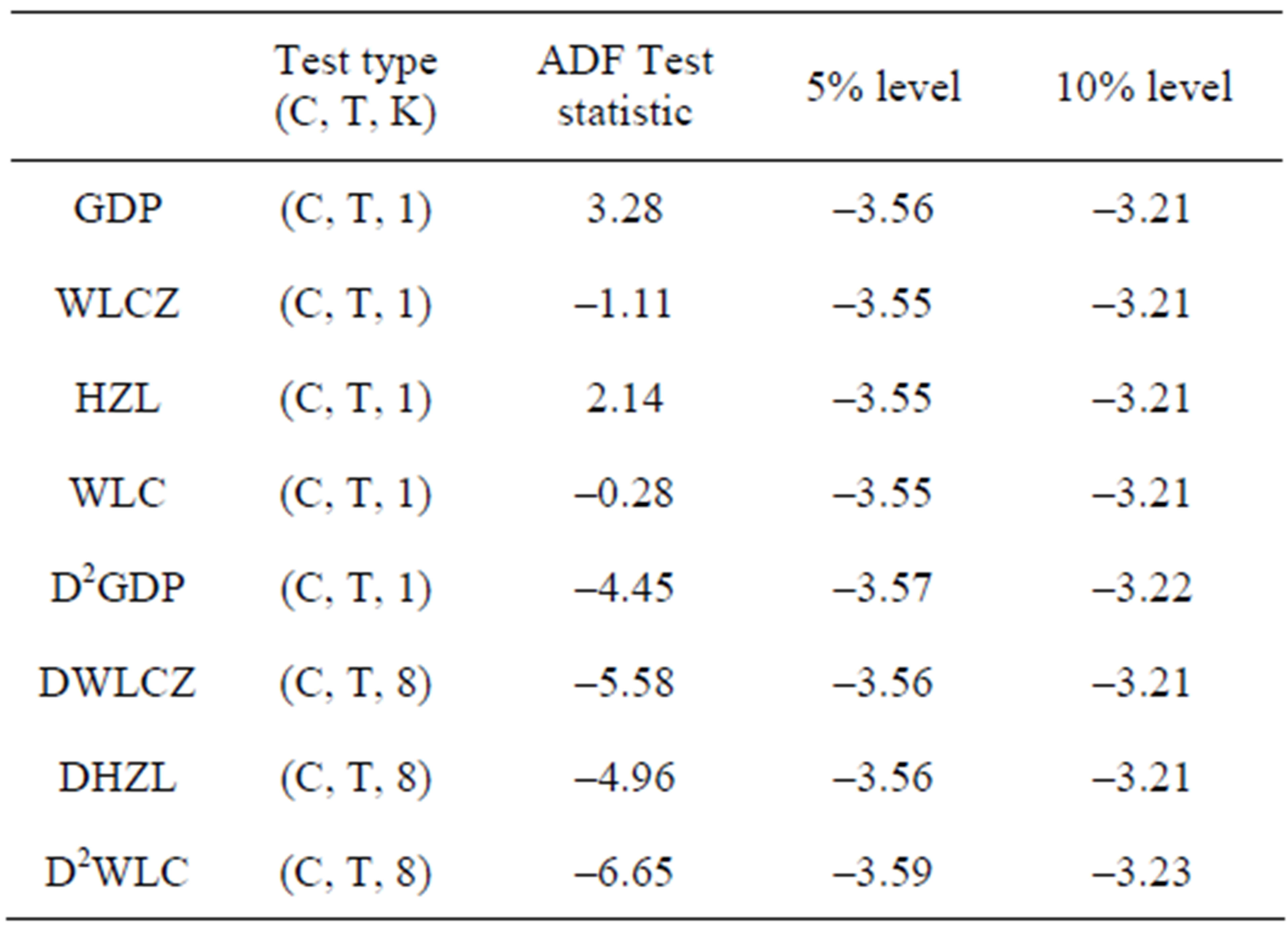
Table 4 Johansen test results.
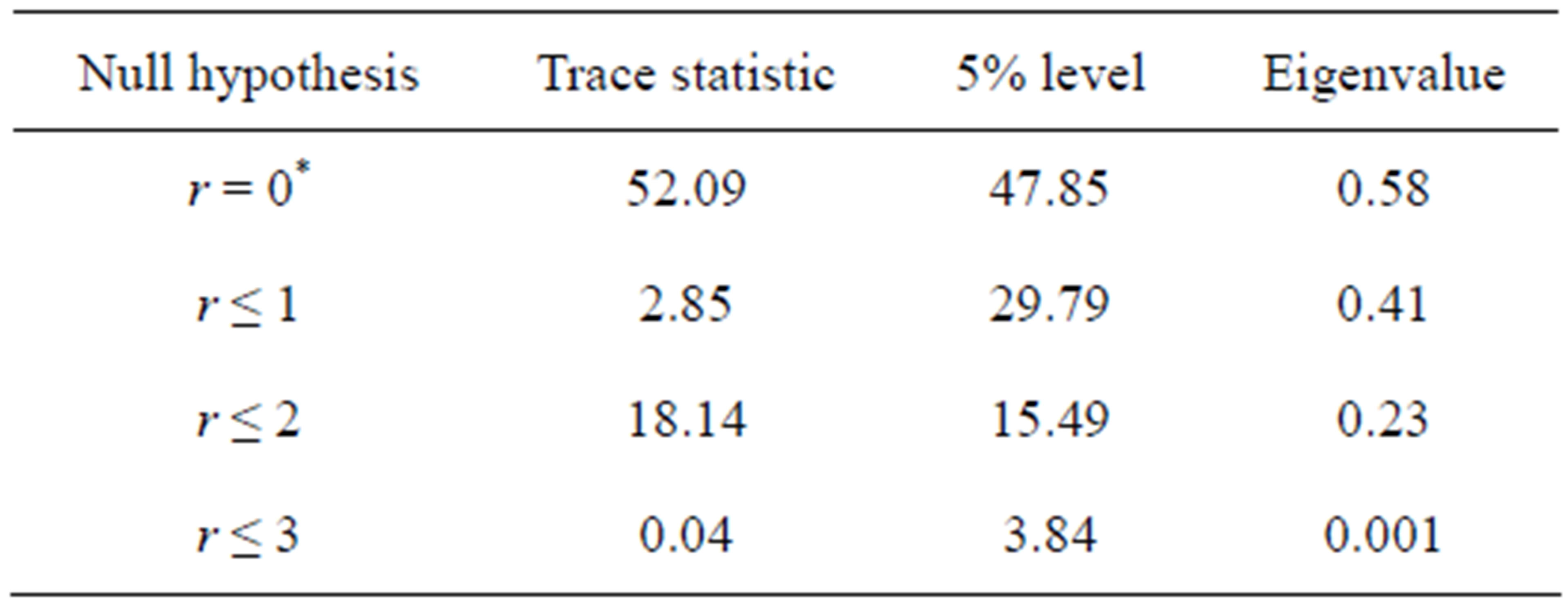
Note: The letters of r means numbers of co-integration equation, *means reject null hypothesis.
This demonstrates that the variable is at least one cointegration equation between the relationships, that there is a long-term equilibrium relationship between variables.
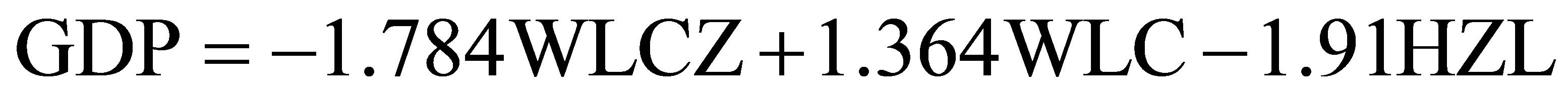 (2.22) (0.88) (0.24) (17)
(2.22) (0.88) (0.24) (17)
The above co-integration equation reflects the longrun equilibrium relationship between variables, but cannot fully reflect the short-term changes relationship between variables. Therefore, it is necessary to establish the error correction model (ECM), to estimate short-term changes between variables. Estimated ECM is give as following:
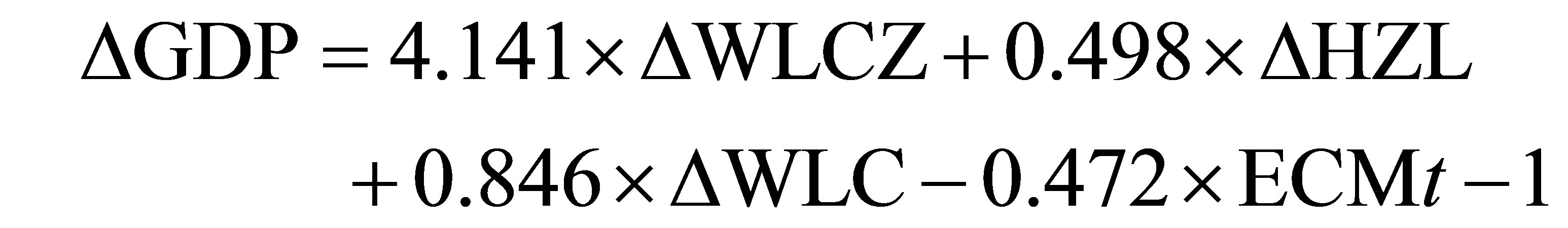 (3.01) (6.84) (1.90) (–2.58) (18)
(3.01) (6.84) (1.90) (–2.58) (18)
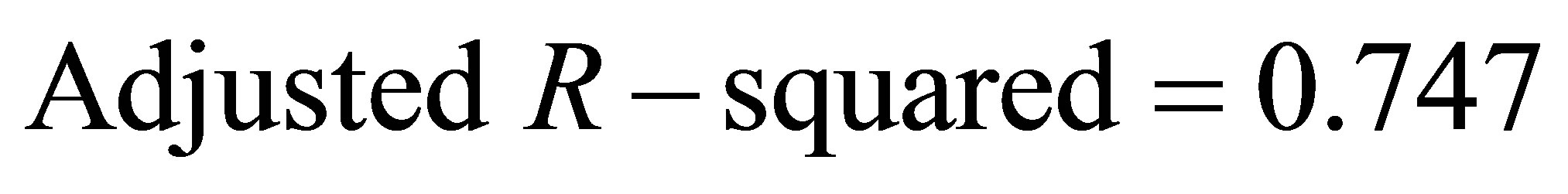
From the equation, T statistics test of all variables are significant in level 10%, the error correction of ECMt-1 coefficient is negative, accord with reverse revision mechanism, thus further shows that the error correction model is good, with residual sequence is the white noise.
By comparing the co-integration equation and ECM, We can conclusion that t compared on short-term, freight turnover (HZL) have negative influence on the GDP in long term, but its elasticity coefficient is greater than the short-term elastic coefficient; Output value of logistics (WLCZ) have short-term elastic significantly greater than its long-term flexibility to GDP, and both have different symbols, changes of direction that does not accordance, it indicates that in recent years the logistics infrastructure investment lead to the logistics industry close to a saturation stage in Fujian province, although output value of logistics (WLCZ) promote the growth of GDP in short-term, but due to the expansion of the regular, the GDP growth plays a role of obstacles in the long term.
6. Conclusions
In this present paper, it has been proposed that the effective method for LRP using a hybrid algorithm based on clustering analysis and chaos search. Through computer simulations the method has been shown to solve largescale LRP. Using the clustering technique, the computational cost is dramatically reduced. Due to the feature of chaotic global ergodicity, the optimal routes are randomly seeked in one cluster, which ensures search efficiently and produces optimal solutions (or near optimal solutions) without local optimization. Thus, the emphasis is directed towards developing a methodology, which has been improved the quality of solution.
The application to other combinatorial optimization problems should be investigated in integrated logistics. The relationship is given with regional logistics and its development. There exists a long-term equilibrium relation between economics growth and logistics development in Fujian province.
7. Acknowledgments
This paper was supported in part by National Natural Science Foundation of China under grant number 71040009, in part by Program for New Century Excellent Talents in University under grant number NCET-10- 0118, in part by Youth Foundation of Chinese Education by HuoYing-dong under grant number 104009.
REFERENCES
- J. H. Bookbinder and K. E. Reece, “Vehicle Routing Considerations in Distribution System Design,” European Journal of Operation Research, Vol. 37, No. 2, 1988, pp. 204-213. doi:10.1016/0377-2217(88)90330-X
- D. B. Bruno, F. Vincent, S. Paul, K. Philip and P. Patrick, “Solving Vehicle Routing Problems Using Constraint Programming and Metaheuristics,” Journal of Heuristics, Vol. 6, No. 4, 2000, pp. 501-523. doi:10.1023/A:1009621410177
- V. Campos and E. Mota, “Heuristic Procedures for the Capacitated Vehicle Routing Problem,” Computational Optimization and Applications, Vol. 16, No. 3, 2000, pp. 265-277. doi:10.1023/A:1008768313174
- L. Cooper, “The Transportation-Location Problem,” Operations Research, Vol. 20, No. 1, 1972, pp. 94-108. doi:10.1287/opre.20.1.94
- G. Dijin, “Hybrid Evolutionary Method for Capacitated Location-Allocation Problem,” Computer and Industrial Engineering, Vol. 33, No. 3-4, 1997, pp. 577-580.
- V. Fernando and A. Joaquin, “Homoclinic Chaos in Inverted Pendula,” Proceeding of the 39th IEEE Conference On Decision and Control, Sydney, 12-15 December 2000, pp. 4821-4822.
- H. Heung-Suk, “Design of Supply-Chain Logistics System considering Service Level,” Computers and Industrial Engineering, Vol. 43, No. 7, 2002, pp. 283-297. doi:10.1016/S0360-8352(02)00075-X
- G. Laporte, “Hamiltonian Location Problems,” European Journal of Operation Research, Vol. 12, No. 1, 1983, pp. 80-87. doi:10.1016/0377-2217(83)90182-0
- G. Laporte and Y. Nobert, “An Exact Algorithm for Minimizing Routing and Operating Costs in Depot Location,” European Journal of Operation Research, Vol. 6, No. 2, 1986, pp. 224-226. doi:10.1016/0377-2217(81)90212-5
- J. Ra, “Dissipative Enterprises, Chaos, and the Principles of Lean Organizations,” Omega, Vol. 26, No. 6, 1998, pp. 397-340.
- C. Watson-Gandy and P. Dohrn, “Depot Location with van Salesmen—A Practical Approach,” Omega, Vol. 1, No. 3, 1973, pp. 321-329. doi:10.1016/0305-0483(73)90108-4
- P. N. William and J. B. Wesley, “Solving the Pickup and Delivery Problem with Time Windows Using Reactive Tabu Search,” Transportation Research Part B, Vol. 34, No. 2, 2000, pp. 107-121. doi:10.1016/S0191-2615(99)00016-8
NOTES
1The demand or supply is known and stable during a period of time.

