American Journal of Operations Research
Vol.2 No.3(2012), Article ID:22428,8 pages DOI:10.4236/ajor.2012.23040
A Decision Aid Approach for Optimisation Problems Involving Several Economic Functions
Department of Decision Sciences, University of South Africa, Pretoria, South Africa
Email: rangomj@unisa.ac.za
Received March 31, 2012; revised April 30, 2012; accepted May 11, 2012
Keywords: Database; Decision Support System; Model-Base; Multi-Objective Program; Pareto Optimality; Software
ABSTRACT
Many concrete real life problems ranging from economic and business to industrial and engineering may be cast into a multi-objective optimisation framework. The redundancy of existing methods for solving this kind of problems susceptible to inconsistencies, coupled with the necessity for checking inherent assumptions before using a given method, make it hard for a nonspecialist to choose a method that fits well the situation at hand. Moreover, using blindly a method as proponents of the hammer principle (when you only have a hammer, you want everything in your hand to be a nail) is an awkward approach at best and a caricatural one at worst. This brings challenges to the design of a tool able to help a Decision Maker faced with these kinds of problems. The help should be at two levels. First the tool should be able to choose an appropriate multi-objective programming technique and second it should single out a satisfying solution using the chosen technique. The choice of a method should be made according to the structure of the problem and to the Decision Maker’s judgment value. This paper is an attempt to satisfy that need. We present a Decision Aid Approach that embeds a sample of good multi-objective programming techniques. The system is able to assist the Decision Maker in the above mentioned two tasks.
1. Introduction
Mathematical programming is an important tool in the arsenal of means at a Decision Maker’s disposal. Indeed, many real-life problems such as product mix, transportation and blending (see for example in [1-3]), may be cast into a mathematical programming framework. Theoretical underpinnings for mathematical programming, particularly for linear programming, are now well established [4,5]. As a result, a broader array of techniques has been developed. We mention, without any claim to exhaustivity, the simplex algorithm [6], the ellipsoid method [7] and the Karmarkar’s method [8,9] for linear programming; the cutting-plane methods [7] and the penalty methods [10] for nonlinear programming. Software with powerful computational and visualisation capabilities like LINGO [11] and XPRESS have also been developed. All the above-mentioned methods and software rely heavily on the assumption that there is only one economic (utility) function to optimize and that all involved parameters have well-known fixed values. In many concrete real-life problems like in public decision-making, water quality management, portfolio optimization to mention but a few, the Decision Maker has to incorporate simultaneously several conflicting economic functions in an optimization.
Setting (see for example in [12,13]. The simplistic approach, consisting of substituting arbitrarily a single objective function to several conflicting ones, often leads to a bad caricature of the reality. Such an approach has no other option but to churn out meaningless outcomes. The purpose of this paper is twofold. Firstly, it aims at raising awareness of the most important techniques used to single out satisfying solutions for a mathematical program with several conflicting goals. Secondly, it describes a Decision Support System (DSS) for multi-objective programming problems (DSS4MOPP) able to help a user confronted with such a problem. The system should assist at two levels. Firstly, to choose an appropriate technique for solving the problem at hand and secondly to single out a satisfying solution that meets the Decision Maker’s needs. The remaining of this paper is organized as follows: The next section introduces basic concepts on multi-objective section, we describe the most used methods for solving multi-objective programming problems. Section 3 is devoted to the design of our DSS for multiobjective programming problems. Finally, we make some concluding remarks along with suggestions for further developments in the field of multi-objective programming.
2. Multi-Objective Programming Problems
2.1. Problem Formulation
A multi-objective program is a problem of the type:
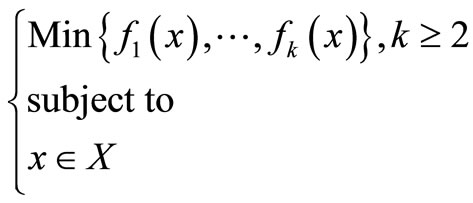 (P)
(P)
where fi(i = 1, 2, ···, k) are real-valued functions of Rn and X is a nonempty and bounded region included in Rn.
2.2. Solution Concept
In multi-objective optimisation context, unless the objective functions are not conflicting, the optimum optimrum does not exist. So we should make explicit the meaning of optimality in this context. Several solution concepts are discussed in the literature. For our purpose we restrict ourselves to the notion of Pareto optimality which is lost used in this context.
Definition 1.  is said to be Pareto Optimal solution for (P) if there does not exist another
is said to be Pareto Optimal solution for (P) if there does not exist another 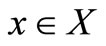 that is at least best as x* for all objective functions and that is best to x* for at least one of them.
that is at least best as x* for all objective functions and that is best to x* for at least one of them.
Definition 2. A vector is said to be locally Pareto optimal for (P) if it is Pareto optimal for (P) in a neighborhood of x*: That is,
is said to be locally Pareto optimal for (P) if it is Pareto optimal for (P) in a neighborhood of x*: That is, 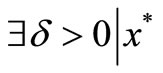 is Pareto optimal for (P) in
is Pareto optimal for (P) in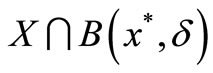 , where
, where
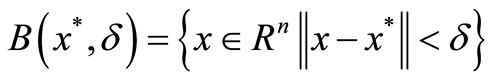 .
.
2.3. Example of a Concrete Problem That May Be in the Form of Multi-Objective Programming Problems
2.3.1. Problem Description
The Nyarutarama Lake, located in Kigali City, is famous for its flora which attracts migratory birds and fish. The lake is connected to many rivers. The most important ones: Karenge, Kimisagara and Nyabarongo are controlled by reservoir. These reservoirs are managed by Rwanda Water and Sanitation Corporation (RWASCO). They provide drinking and irrigation fresh water to the Nyarutarama lake. The problem consists of determining optimal release from different reservoirs while meeting drinking and irrigation water needs.
2.3.2. Mathematical Formulation of the Problem
For this problem we can consider as decision variables: water releases, from different reservoirs, for irrigation, Ii,t, Di,t for drinking, Di,t and for the Nyarutarama Lake Li,t where i and t are reservoir and time indices respectively. Moreover the following parameters variables must be introduced in order to solve the problem Mi,t. Estimation of releases for drinking, irrigation and the lake from reservoir i at period t: MRLt: Minimum releases for the lake at period t specified by the Environment Ministry. DD,i,t: Maximum demand for drinking water from reservoir i at the end of period t: DI,i,t: Maximum demand for irrigation water from reservoir i at the end of period t: In this problem, the period t is equal to one month and the index I is equal to 1 for Karenge reservoir, to 2 for Kimisagara reservoir and to 3 for Nyabarongo reservoir. The optimisation problem corresponding to the water management in subsection 2.3.1:

subject to
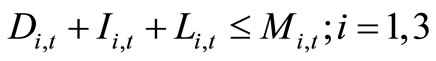 (1)
(1)
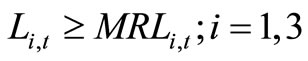 (2)
(2)
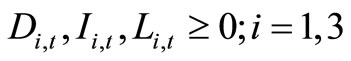 . (3)
. (3)
where (1) are constraints on maximum releases, (2) are constraints on lake releases and (3) non-negativity constraints.
3. Methods for Solving Multi-Objective Programming Problems
In the literature (see for example [1,14]), the most used methods for solving multi-objective programs are grouped in five categories, namely No-preference methods, a Priori methods, a Posteriori methods, Interactive methods and Metaheuristics. In what follows we briefly discuss each category.
3.1. No-Preference Methods
The No-Preference methods do not need any inter objective or subjective preference information from the Decision Maker once the objectives of the problem have been defined. The methods in this category include Compromise Programming [15-17] and Multi-objective Proximal Bundle method [3,18].
3.2. A Priori Methods
Unlike No-preference methods, the general principle of a Priori methods is to first take into consideration the opinions and preferences of the decision maker before solving the multi-objective program. The Analyst solve the resulting problem by methods such as Goal Programming and Lexicographic goal programming [19] and present the solution to the Decision Maker.
3.3. A Posteriori Methods
A Posteriori methods are concerned with finding all or most of the Pareto optimal solutions of a given multiobjective program. These solutions are then presented to the Decision Maker who has to choose one of them. The most important a Posteriori methods described in the literature include e-constraint method [16,17], Adaptive search method [17], Hybrid method [16,20], Benson’s method [1] and the Weighting method [21].
3.4. Interactive Methods
With interactive methods the Analyst starts with an intial solution, discuss with the Decision Maker and obtain a new solution or a set of new solutions if the Decision Maker is not happy with the current one. Here are among others some interactive methods: Step method ([17], [22, 23]) Sequential Proxy Optimization Technique (SPOT) [24], Interactive Surrogate Worth Trade-off (ISWT) method [17] Geoffrion-Dyer-Feinberg (GDF) method ([17,25]), Reference Point(RP) method [26] and Nondifferentiable Interactive Multi-objective BUndle-based optimization System(NIMBUS) method [17].
3.5. Meta-Heurestics
Most of the methods described before apply for convex multi-objective programs. In the case of non convex multi-objective programs metaheuristic methods may be considered [27,28]. A meta-heuristic is a method that seeks to find a good solution to a problem at a reasonable computational cost. A meta-heuristic often has an intuittive justification and therefore a mathematical proof cannot be constructed to guarantee the Pareto optimality of the solution found [28]. The most used meta-heuristic methods are Simulated Annealing [29], Tabu Search [30] and Genetic Algorithm (GA) [28].
4. A Decision Support System for Multi-Objective Programming Problems
In this section we present our own decision support system for multiobjective programming problems. This system is named DSS4MOPP [31].
4.1. Components for DSS4MOPP
DSS4MOPP has three main components, namely a database, a modelbase and a software system. In the following subsections we briefly describe each of these components.
4.1.1. Database
DSS4MOPP database stores a collection of data files. These data files contain a combination of numerical and alphabetical data. Although some of the data is stored directly in the computer, some of it may be stored on the internet. The files are protected by a security code activated by the Decision Maker.
4.1.2. Modelbase
The modelbase of DSS4MOPP consists of the following multiobjective programming methods: the compromise programming method, the genetic algorithm, the goal programming method, the lexicographic goal programing method, the method for generating efficient solutions, the multi-objective proximal bundle method, the NIMBUS method, the reference point method and the weighting method. These methods are the most realistic used methods. The tools used to develop DSS4MOPP are Linear Interactive Discrete Optimizer (LINDO) [11], non-differentiable interactive multi-objective bundle-based optimization system (NIMBUS) [12] and Multi-Objective Programming Envelopment (MOPEN) [15]. These tools were chosen due to their availability and afford-ability.
4.1.3. Software Subsystem
The software subsystem of DSS4MOPP consists of three components: data base management software (DBMS), model base management software (MBMS) and Dialogue Generating Management Software (DGMS). Through these components, the interface with the analyst is realised by a sequence of windows, with each window being regarded as a step. The dialogue generating management system ensures that there is interaction between the DSS4MOPP, the analyst and the operating system.
4.2. Functioning of DSS4MOPP
The inputs into DSS4MOPP are the problem (P) and the views of the Decision Maker about this problem. From these inputs, DSS4MOPP chooses a method and use that method to solve the problem. The detail of the way SS4MOPP works is given in Figure 1. For instance, if (P) is non convex DSS4MOPP solves (P) by Genetic algorithm. If (P) is convex and the Decision Maker has special preferences in a specific order, DSS4MOPP solves (P) by Lexicographic goal programming. If (P) is convex and the Decision Maker has no special preferences in a specific order, DSS4MOPP solves (P) by Proximal bundle method, provided the objective functions are not differentiable. Otherwise, if the objective functions are differentiable, DSS4MOPP solves (P) by Compromise programming method. Figure 1 shows how the rest of the methods are chosen and used by DSS4MOPP.
4.3. Implementation of DSS4MOPP
To build DSS4MOPP we used TextPad [32] program. TextPad is able to edit files up to the limits of virtual memory. Sensitivity analysis is also possible with DSS4MOPP. It also has standard Microsoft Windows applications menu and functions such as “File”, “Edit”, “View”, “Window” and “Help”. These functions facilitate interaction between DSS4MOPP and the analyst.
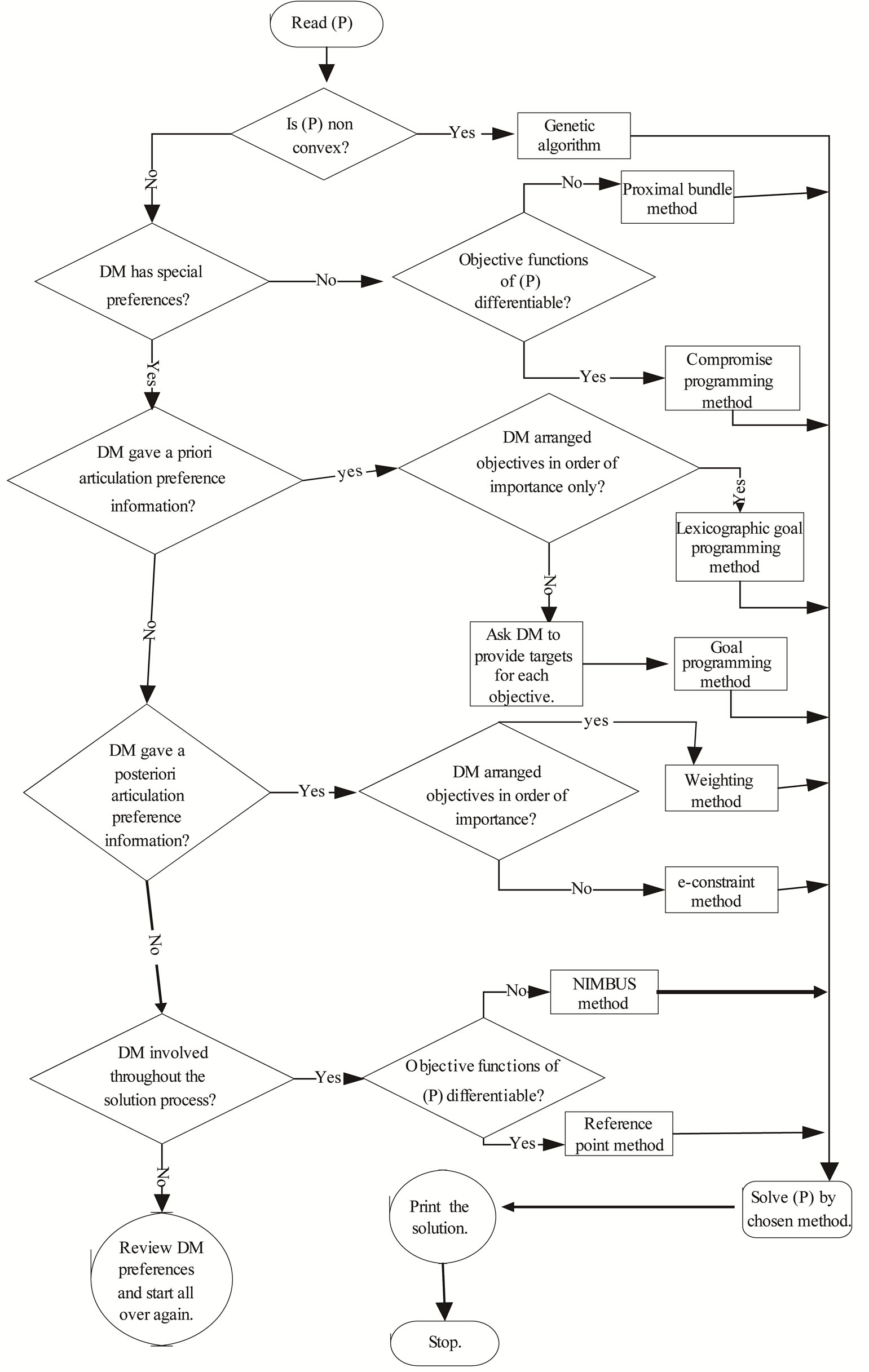
Figure 1. DSS4MOPP functioning flowchart.
Different tools (such as LINGO and MOPEN) for solving problems in DSS4MOPP have been integrated, which provides the analyst with the potential to set the DM’s preferences for the most preferred solution. The interface of DSS4MOPP facilitates the operation of the analyst by offering different alternatives.
5. Example
For the sake of illustration, let us consider the problem described in subsection 2.3. As the targets DD,i,t and DI,i,t are provided by the Decision Maker, for each economic function, the DSS4MOPP will choose Goal Programming method (see Figure 2) and the system solve the following mathematical program (see Figure 3) to obtain the solution (see Figure 4) of the problem under consideration.
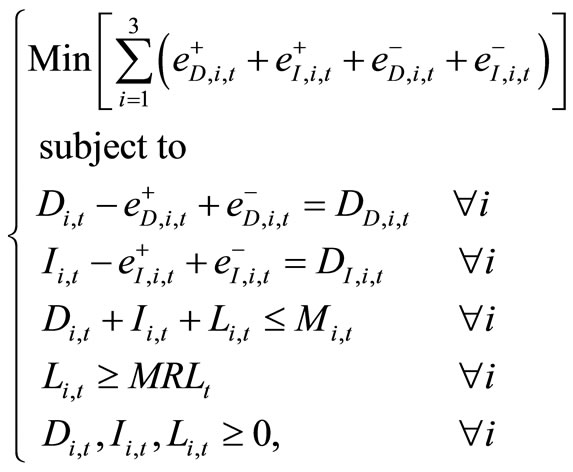
where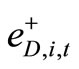 ,
, 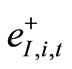 ,
, 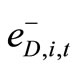 ,
, 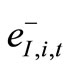 are positive and negative deviations between Di,t and DI,i,t and between Ii,t and DD,i,t respectively. For January 2010 (the month un der investigation), we have the following data expressed in millions of liters of water, have been collected from RWASCO [33].
are positive and negative deviations between Di,t and DI,i,t and between Ii,t and DD,i,t respectively. For January 2010 (the month un der investigation), we have the following data expressed in millions of liters of water, have been collected from RWASCO [33].
With above data and by denoting positive and negative deviations by EDITIV, EIITV, EDITU and EIITU respectively, the system will use the tool to solve this roblem.
Minimise ED1TV + EI1TV + ED1TU + ED2TV + EI2TV +ED2TU + EI2TU + ED3TV + EI3TV + ED3TU + EI3TU, subject to D1,t + ED1TU – ED1TV = 2.9, D2,t + ED2TU – ED2TV = 0.185, D3,t + ED3TU – ED3TV = 0.787, I1,t + EI1TU – EI1TV = 1.613, I2,t + EI2TU – EI2TV = 0.216, I3,t + EI3TU – EI3TV = 0.517, D1,t + I1,t + L1,t ≤ 3.2, D2,t + I2,t + L2,t ≤ 3.2, D3,t + I3,t + L3,t ≤ 3.2, L1,t ≥ 1.8, L2,t ≥ 1.8, L3,t ≥ 1.8.
The solution obtained is D1,t = 0:000, D2,t = 0:0.185, D3,t = 0:0.787, I1,t = 1:400, I2,t = 1:216, I3,t = 1:517, L1,t = 1:800, L2,t = 1:800, L3,t = 1:400.
6. Concluding Remarks
Many concrete real-life situations may be cast into a mathematical programming framework. In most of these situations, one has to combine evidence from disparate sources and as a result grapple with conflicting objective functions. Therefore, multi-objective mathematical programming is a relevant issue. Unfortunately, a multiobjective mathematical program is an illdefined problem. As a matter of fact, the notion of “optimum optimorum” does not apply in this case due to the presence of conflicting utility functions. Lines for further developments
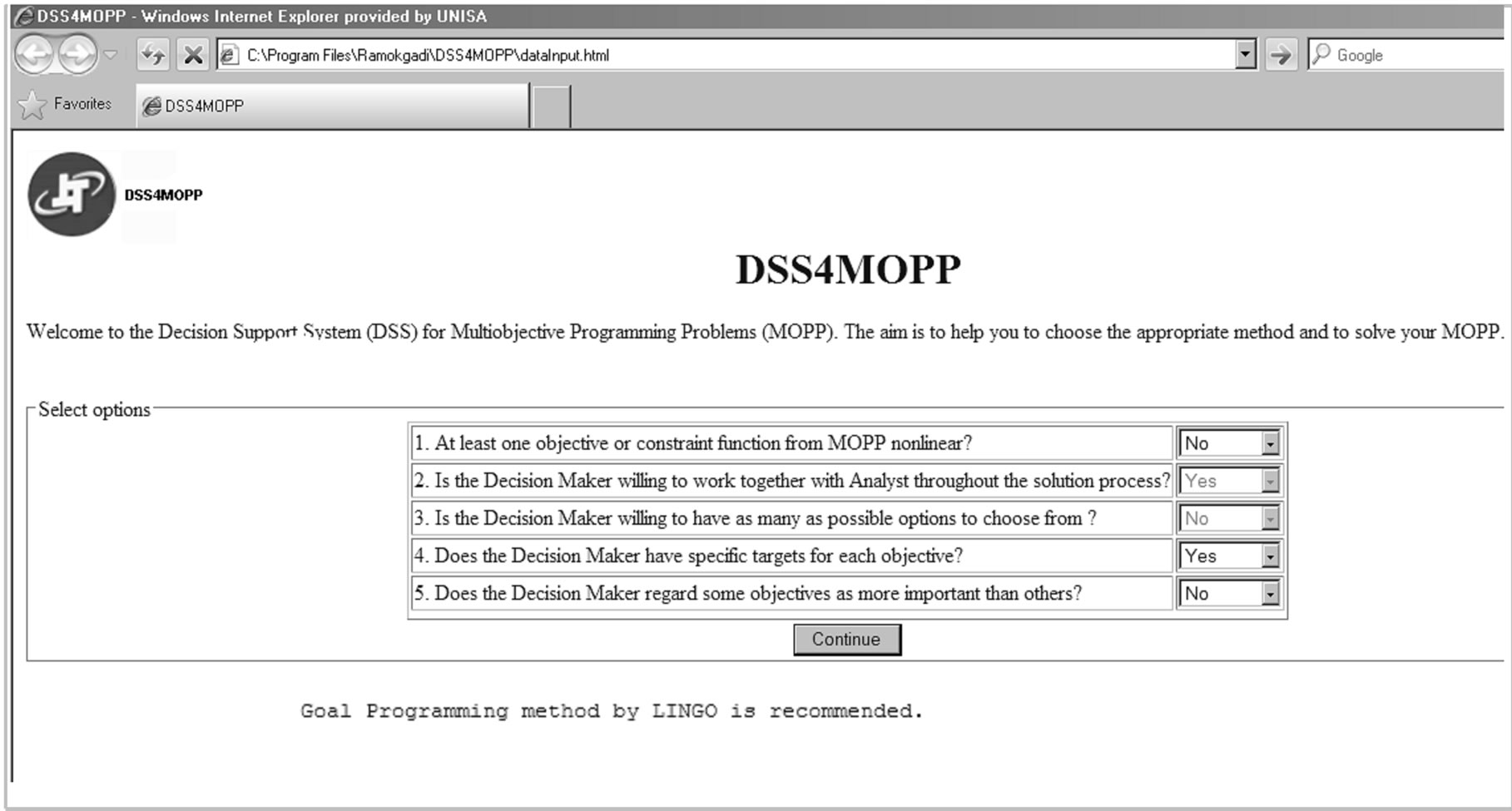
Figure 2. Form-based input page of DSS4MOPP.
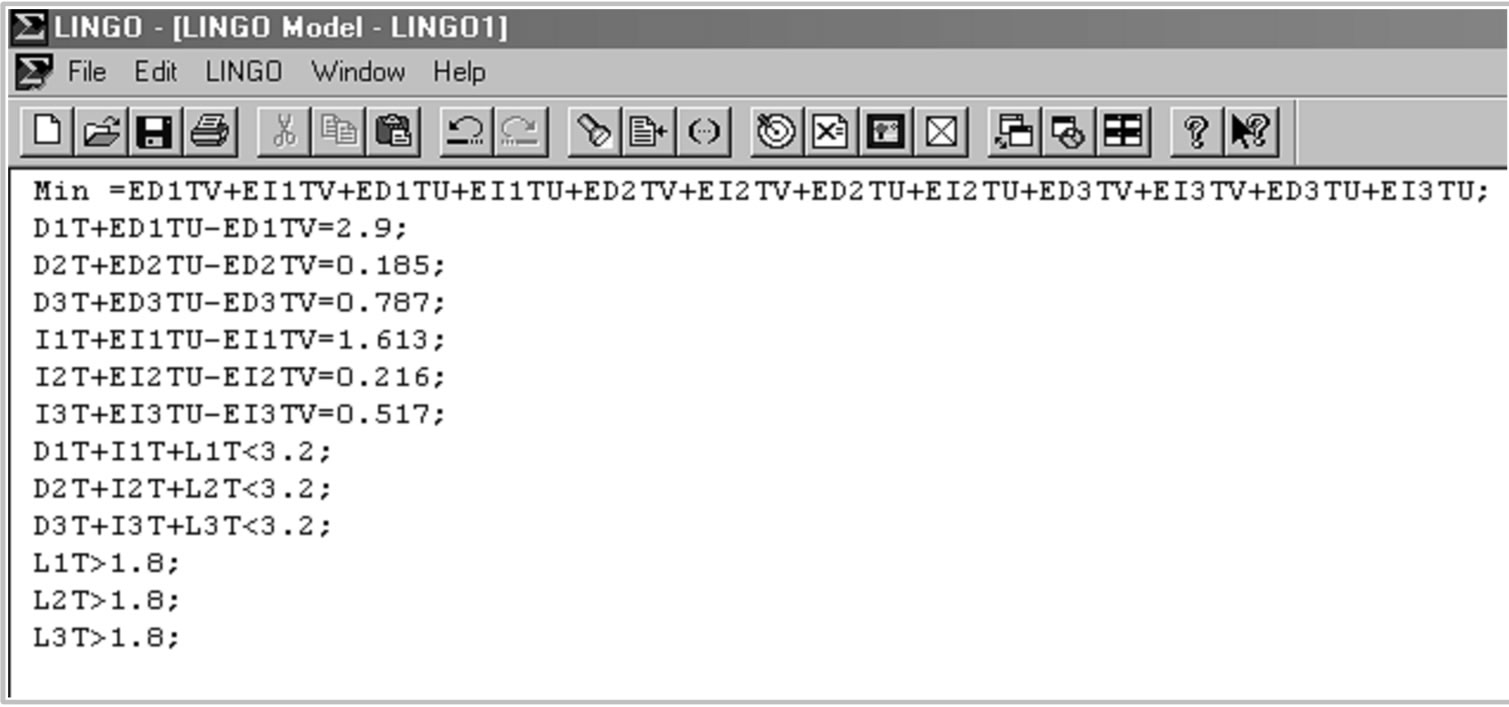
Figure 3. Data is entered in DSS4MOPP.
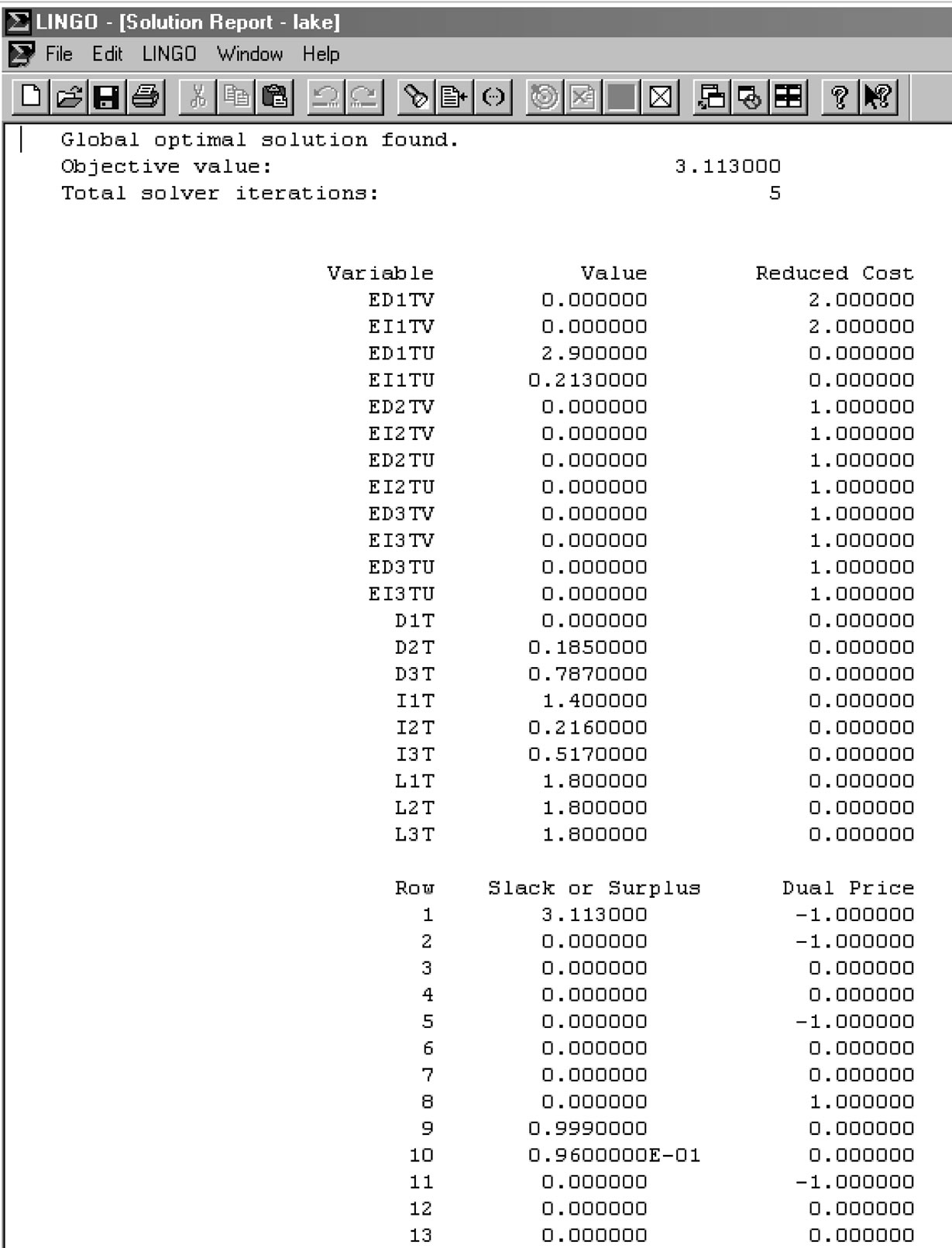
Figure 4. The solution from DSS4MOPP.
in this field include: Enrichment of the system by allowing it to help the Decision Maker throughout the entire decision-making process. Use of language of Fuzzy sets theory to allow some leeways in the constraints satisfaction and to incorporate imprecise data. Severe limitations on objectivity are encountered in solving the above mentioned problem. In such a turbulent environment, the mainstay of rational choice cannot hold and it is virtually impossible to provide a truly meaning of optimal decision in this context. One then resort either to notion of strong, weak, proper Pareto optimality or to satisfying solutions based on the bounded rationality principle. Many methods have been proposed to single out appropriate solutions of a multi-objective programming problems and a Decision Maker may get lost in face of such a pletora of techniques. The purpose of this paper was to discuss how to help a Decision Maker using an appropriate tool for dealing with his problem. In order to achieve this, we have presented a Decision Aid tool called Decision Support System for multi-objective programming problems (DSS4MOPP). This tool helps in two levels. Firstly, it chooses an appropriate multi-objective programming method. Secondly, it singles out a satisfying solution using the chosen method. For the sake of illustration, we have presented an example of water management borrowed from dissertation of [33].
REFERENCES
- K. Deb, “Multi-Objective Optimization Using Evolutionary Algorithms,” John Wiley and Sons, New York, 2001.
- C. L. Hwang and A. S. M. Masud, “Multiple Objective Decision Making: Methods and Applications: A State-ofthe-Art Survey,” Lecture Notes in Economics and Mathematical Systems, Vol. 164, Springer-Verlag, Berlin, Heidelberg, 1979. doi:10.1007/978-3-642-45511-7
- K. M. Miettinen and M. M. Makela, “Interactive BundleBased Method for Non-Differentiable Multi-Objective Optimization: NIMBUS,” Optimization, Vol. 34, No. 3, 1995, pp. 231-246. doi:10.1080/02331939508844109
- K. C. Kiwiel, “A Descent Method for Non-Smooth Convex Multi-Objective Minimization,” Large Scale Systems, Vol. 8, 1985, pp. 119-129.
- B. Render and R. M. Stair, “Quantitative Analysis for Management,” sixth edition, Prentice Hall, New Jersey, 1997.
- G. B. Dantzig, “A Complementary Algorithm for an Optimal Capital Path with Invariant Proportions,” International Institute for Applied Systems Analysis, 1973.
- D. G. Luenberger, “Introduction to Linear and Nonlinear Programming,” Addison-Wesley Publishing Company, Menlo-Park, 1973.
- N. Karmarkar, “A New Polynomial Time Algorithm for Linear Programming,” Combinatorica, Vol. 4, No. 4, 1984, pp. 373-395. doi:10.1007/BF02579150
- W. L. Winston, “Operations Research: Applications and Algorithms,” Third Edition, International Thomson Publishing, California, 1994.
- M. Avriel “Nonlinear Programming Analysis and Methods,” Prentice-Hall, New Jersey, 1976.
- L. Scharage, “Optimization Modeling with LINGO,” Sixth Edition, LINDO Systems Inc., Chicago, 2006.
- K. M. Miettinen and M. M. Makela, “Synchronous Approach in Interactive Multi-Objective Optimization,” European Journal of Operational Research, Vol. 170, No. 3, 2006, pp. 909-922. doi:10.1016/j.ejor.2004.07.052
- G. W. Evans, “An Overview of Techniques for Solving Multi-Objective Mathematical Programs,” Management Science, Vol. 30, No. 11, 1984, pp. 1268-1282. doi:10.1287/mnsc.30.11.1268
- K. M. Miettinen and M. M. Makela, “Optimization System www Nimbus,” Vol. 9, Laboratory of Scientific Computing, Department of Mathematics, University of Jyvaskyla, Finland, 1998.
- R. Caballero, M. Luque, J. Molina and F. Ruiz, “Mopen: A Computational Package for Linear Multi-Objective and Goal Programming Problems,” Decision Support Systems, Vol. 41, No. 1, 2005, pp. 160-175. doi:10.1016/j.dss.2004.06.002
- M. Ehrgott, “Multicriteria Optimization,” 2nd Edition, Springer, Auckland, 2005.
- K. M. Miettinen, “Nonlinear Multi-Objective Optimization,” 1st Edition, Kluwer Academic Publishers, Boston, 1999.
- K. C. Kiwiel, “Proximity Control in Bundle Methods for Methods for Convex Non-Differentiable Minimization,” Mathematical Programming, Vol. 46, No. 1-3, 1990, pp. 105-122. doi:10.1007/BF01585731
- F. Amador and C Romero, “Redundancy in Lexicographic Goal Programming: An Empiricalapproach,” European Journal of Operational Research, Vol. 41, No. 3, 1989, pp. 347-354. doi:10.1016/0377-2217(89)90255-5
- R. Chelouah and P. Siarry, “A Hybrid Method Combining Continuous Tabu Search and Nelder-Mead Simplex Algorithms for the Global Optimization of Multiminima Functions,” European Journal of Operational Research, Vol. 161, No. 3, 2005, pp. 636-654. doi:10.1016/j.ejor.2003.08.053
- M. Gershon, “The Role of Weights and Scales in the Application of Multi-Objective Decision Making,” European Journal of Operational Research, Vol. 15, No. 2, 1984, pp. 244-250. doi:10.1016/0377-2217(84)90214-5
- R. Benayoun, J. de Montgolfier and J. Tergny, “Linear Programming with Multiple Objective Functions: Step Method (Stem),” Mathematical Programming, Vol. 1, No. 1, 1971, pp. 366-375. doi:10.1007/BF01584098
- L. R. Gardiner and R. E. Steuer, “Unified Interactive Multiple Objective Programming,” European Journal of Operational Research, Vol. 74, 1984, pp. 371-406.
- J. T. Buchanan, “Multiple Objective Mathematical Programming: A Review,” New Zealand Operational Research, Vol. 14, No. 1, 1986, pp. 1-27.
- A. M. Geoffrion, “Proper Efficiency and the Theory of Vector Maximization,” Journal of Mathematical Analysis and Applications, Vol. 22, No. 3, 1968, pp. 619-630. doi:10.1016/0022-247X(68)90201-1
- M. I. Henig and Z. Ritz, “Multiplicative Decision Rules for Multi-Objective Decision Problems,” European Journal of Operational Research, Vol. 26, No. 1, 1986, pp. 134-141. doi:10.1016/0377-2217(86)90165-7
- A. K. Bhunia and J. Majumdar, “Elitist Genetic Algorithm for Assignment Problem with Imprecise Goal,” European Journal of Operational Research, Vol. 177, 2007, pp. 684-692. doi:10.1016/j.ejor.2005.11.034
- C. Botha, E. Ferreira, G. Geldenhuys and H. Ittman, “Selected Topics in Operations Research: Quantitative Management,” UNISA, Pretoria, 1998.
- C. D. Gelatt, S. Kirkpatrick and M. P. Vecchi, “Optimization by Simulated Annealing,” Science, Vol. 220, No. 459, 1983, pp. 45-54.
- J. W. Barnes, F. W. Glover and M. Laguna, “Tabu Search Methods for a Single Machinescheduling Problem,” Journal of Intelligent Manufacturing, Vol. 2, No. 2, 1991, pp. 63-74. doi:10.1007/BF01471219
- M. J. Rangoaga, “A Decision Support System for MultiObjective Programming Problems,” Master’s Thesis, University of South Africa, Pretoria, 2009.
- H. S. Solutions, “Textpad,” 1992. http://wapedia.mobi/en/textpad
- S. S. Ruzibiza, “Solving Multi-Objective Mathematical Programming Problems with Fixed and Fuzzy Coefficients,” Master’s Thesis, Independent Institute of Lay Aventists of Kigali, Kigali, 2011.

