ABSTRACT

We investigate the evolution of initial entangled two-atom in cavity with single-mode light field. Using the method of negative eigenvalue of partially transposed matrix we analysis the evolution of the entanglement of the two-atom in a field of number state and Kerr-media environment and find that entanglement sudden death phenomenon occurs in the number of particles field. When the atoms interact with the Kerr medium, we obtain that the phenomenon of sudden death can be eliminated in the particle-number field, and the entanglement of two-atom oscillates around a high-value.

1. Introduction

Quantum information science, which mainly includes quantum computer and quantum communication, has increasingly evolved as a new object. In the past few years, quantum information has made a surprise progress both in theoretical and experimental fields. It has created many miracles, such as absolute secure quantum key, quantum dense coding, quantum teleportation, and so on. Recently the theory of quantum information has been widely used to every branch of physics, which has acelerated the development of information science and technology. Jaynes-Cummings mode (J-C mode) and Tavis-Cummings model (T-C mode) could in deal the quantum optics and quantum information problems effectively. In special condition, they have analytic solutions, so they have theoretical and real meanings, and have been afforded more and more attention. Now the study of quantum entanglement becomes more important, such as the quantum teleportation due to quantum entanglement, which acts as quantum channel to join different space sites [1-5]. Yu and Eberly [6] found Entanglement Sudden Death, it made widely concern about the theory [7,8] and experiment [9-11]. In this letter we analysis the two-atom entanglement characteristics in Numerical1 state field and Kerr-media environment.

2. Model and Method

2.1. Theoretical Model

One of the initial entangled two-atom interact with a cavity in the single-mode light field. We can use the J-C mode to describe the action of atom and light field. The Hamiltonian of this system can be described as

(1)

Here is essential transition frequency of atom and is the frequency of light field; g is coupling constant of atom and light field. 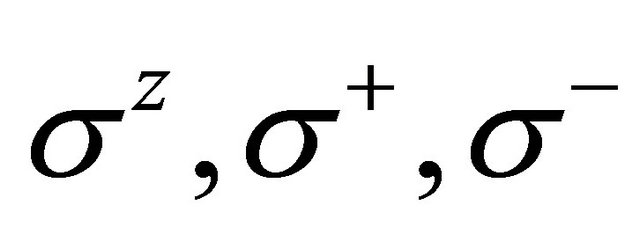is spin operator of atom that,

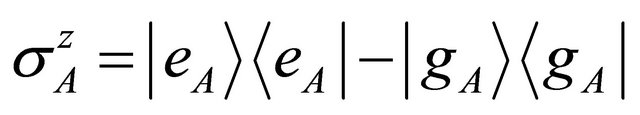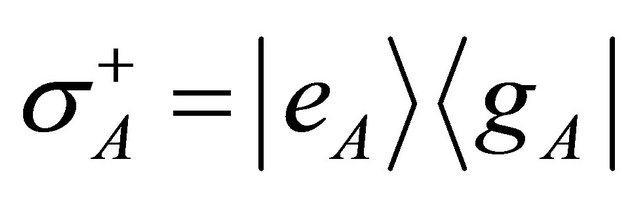, and

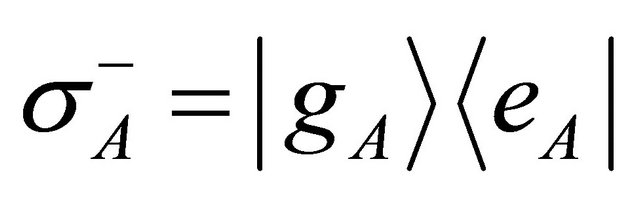, which is excited state and base state of atom.

In this letter we discussed the entanglement state of two-atom. The initial state can be written as

(2)

At any time in the interaction picture, the state of system is depicted as

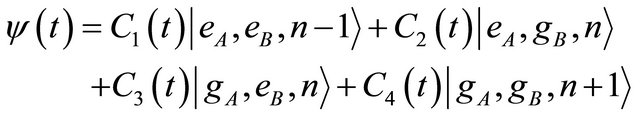
In the interaction picture, the Schrödinger equation of system is

(3)

Using the initial condition we can get

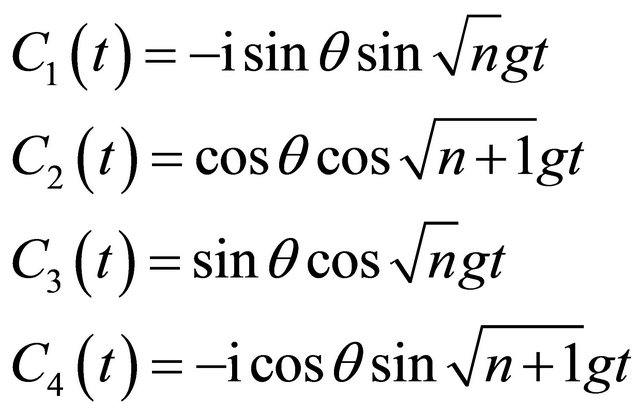(4)

2.2. Calculation

We analysis the two-atom entanglements characteristics in a vacuum field by using the partially transposed matrix of negative Eigen values (negativity) method [12]. It is defined as

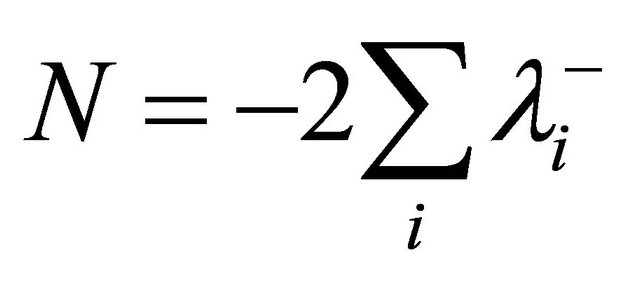(5)

Which 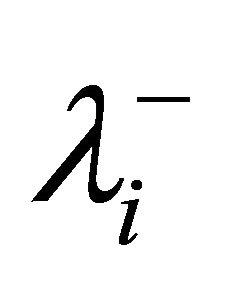is negative Eigen values of the partially transposed matrix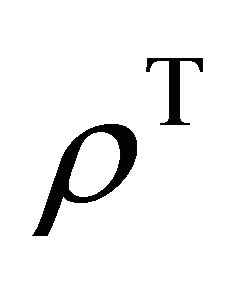, and. By this calculation method we get the result as follows.

(6)

The evolution of entanglement degree of the system is described as Figure 1.

2.3. The Effect of Kerr Medium

When the cavity with single-mode numerical light field fills with Kerr medium, the Hamiltonian of the system can be written as

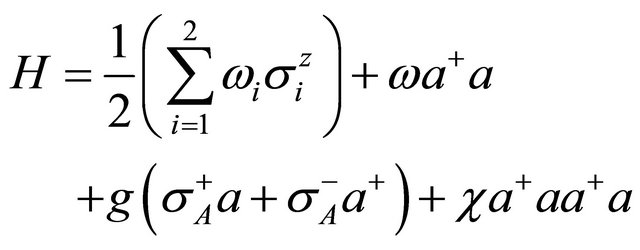(5)

which describes the strength of interaction between Kerr medium and light field.

As the initial state is

(6)

At any time in the interaction picture, the state of system is depicted as

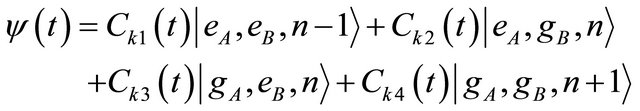(7)

2.4. Calculation and Discussion

The two-atom entanglement characteristics in a vacuum field, using the partially transposed matrix of negative eigenvalues (negativity) method [12], it is defined as

(8)

The evolution of entanglement degree is described as Figures 1 and 2.

According to the picture we can see that the entanglement degree of the two-atom declines seriously in the number of particles field; sometimes sudden death of entanglement occurs (as it is shown in Figure 1). The regions of entanglement sudden death increase by the increasing particle number. The reason is that the action between atom and light field destroys the entanglement of the atoms. For the further study, we find that Kerr medium can erase the phenomenon of sudden death entanglement in numerical light field when two entangled atoms enter-act in the environment of Kerr medium and single-mode numerical light field (as it is shown in Fig-

ure 2). Further more, it can make the entangled atoms keep high entanglement degree, and can make the evolution of them near the maximal entanglement regions.

3. Conclusion

From the above discussion, we find that the entanglement degree decreases seriously when the entangled atoms are in the number of particles field. Sometimes entanglement sudden death phenomenon occurs. Especially we obtain that the phenomenon of entanglement sudden death can be eliminated in the particle-number field, and the entanglement of two-atom oscillates around a high-value state under a certain condition when the light field is filled with the Kerr medium. It means that Kerr medium could change the regions of disentanglement and could improve entanglement degree.

4. Acknowledgements

Thanks for the discussion with Doctor Zhang Yingjie and associate professor Han feng. Otherwise this work was supported by the National Natural Science Foundation of China (10774088, 10947006) of Doctor Yunjie Xia and Zhongxiao Man.

REFERENCES

NOTES

¹Foundation of Natural Science Foundation of China (11147019) and Jining University (Grant No. 2010QNKJ02).