Journal of Crystallization Process and Technology
Vol.4 No.2(2014), Article ID:45434,8 pages DOI:10.4236/jcpt.2014.42016
Studies on Nano Crystalline Ceramic Superconductor LaZrYBaCa2Cu3O11 at Three Different Temperatures
Anitha S. Nair1, Vinila V. S.2, Sheelakumari Issac3, Reenu Jacob4, Anusha Mony2, Harikrishnan G. Nair2, Sam Rajan4, Satheesh D. J.2, Jayakumari Isac4*
1Department of Physics, D.B. College, Parumala, India
2Centre for Condensed Matter, Department of Physics, CMS College, Kottayam, India
3Department of Chemistry, UC College, Aluva, India
4Department of Physics, CMS College, Kottayam, India
Email: *drjayacmscollege@gmail.com, *jayacms@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 3 February 2014; revised 3 March 2014; accepted 10 March 2014
ABSTRACT
The high temperature superconductors are ceramic materials with layers of Copper-oxide spaced by layers containing Barium and other atoms. The Yttrium compound is somewhat unique in that it has a regular crystal structure while the Lanthanum version is classified as a solid solution. The Yttrium compound is often called the 1-2-3 superconductor because of the ratios of its constituents. Lanthanum Zirconium Yttrium Barium Calcium Copper Oxide (LaZrYBaCaCuO) was prepared by the usual solid state reaction method. In order to show the viability of the proposed method, super-conducting powder was prepared in special furnace. The sample was analyzed by X-ray Diffraction (XRD), Particle size determination, SEM and EDX. The comparison of XRD results with JCPDS files confirmed the orthorhombic structure of the sample with a ≠ b ≠ c and α = β = γ = 90˚. Scanning Electron Microscopy (SEM) studies revealed that its particle size is in the nanometer range. It also confirmed the calculated value of particle size from Debye Scherrer’s formula. EDX spectrum shows the elements of the sample. X-ray instrumental peak broadening analysis was used to evaluate the size and lattice strain by the Williamson-Hall Plot method.
Keywords:Lanthanum Zirconium Yttrium Barium Calcium Copper Oxide (LaZrYBaCaCuO), XRD, SEM, EDX, Debye Scherrer’s Formula, Instrumental Broadening, Williamson-Hall Plot Method

1. Introduction
Ceramic materials are brittle, hard, strong in compression, weak in shearing and tension. They withstand chemical erosion that occurs in an acidic or caustic environment. In many cases withstanding erosion from the acid and bases applied to it. Ceramics generally can withstand very high temperatures such as temperatures that range from 1000˚C to 1600˚C (1800˚F to 3000˚F). At low temperatures, La2O3 has an A-M2O3 hexagonal crystal structure. The La3+ metal atoms are surrounded by a 7 co-ordinate group of O2-atoms, the oxygen ions are in an octahedral shape around the metal atom and there is one oxygen ion above one of the octahedral faces Yttrium oxide (Y2O3) nanoparticle is an air-stable, solid substance white in color. In this work the authors describe the preparation of LaZrYBaCaCuO ceramic material and characterized to show good quality, homogeneity and the desired stoichiometry of the sample prepared. The results were analyzed by X-ray diffraction (XRD), SEM, EDX. The particle size was determined from XRD details by Debye Scherrer formula. The SEM studies revealed that its particle size is in hundred nanometer range. The EDX spectrum of LaZrYBaCaCuO gave the information on the elemental composition of the material. The particle size and strain of the material was found by Instrumental Broadening and Williamson-Hall Plot method.
2. Materials and Experimental Methods
LaZrYBaCaCuO has perovskite structure. The perovskite structure is adopted by many oxides. The representative structure of perovskite compounds is cubic, the compounds in this family may possess some distortion. The orthorhombic and tetragonal phases are most common variants. Figure 1 shows the structure of LaZrYBaCaCuO and TC of some related high temperature superconductor materials.
Calcium-doped ceramics with the chemical formula LaZrYBaCa2Cu3O11 were prepared by the conventional solid state reaction technique according to the molecular formula. For the prepared sample, the reagent grade chemicals of high purity (99.99%) Lanthanum oxide, Zirconium oxide, Yittrium oxide, Barium carbonite, Calcium oxide and Copper oxide powders were used as the raw materials and weighed according to their molecular formula.
The powders of the required ceramics were mixed mechanically. Mechanical mixing is usually done by hand mixing in agate mortar for very long time. Then ball milled with suitable balls to insure homogeneity and milling. Then the material calcined at different temperatures, 500˚C and 950˚C. After the furnace is off, on cooling the oxygen is allowed to flow into the furnace at intervals (Oxygen Annealing). A final furnace temperature of 950˚C is maintained after the intermediate firings. A temperature much higher than this will result in a material that is much harder to regrind. Temperatures above 1030˚C may destroy the crystal structure. Then X-ray diffraction spectrum of these materials was taken. For experimental conformation of the calculated particle size value, Scanning Electron Microscopy (SEM) photograph was taken. From EDX, the composition details of the prepared ceramics were determined.
2.1. XRD Analysis
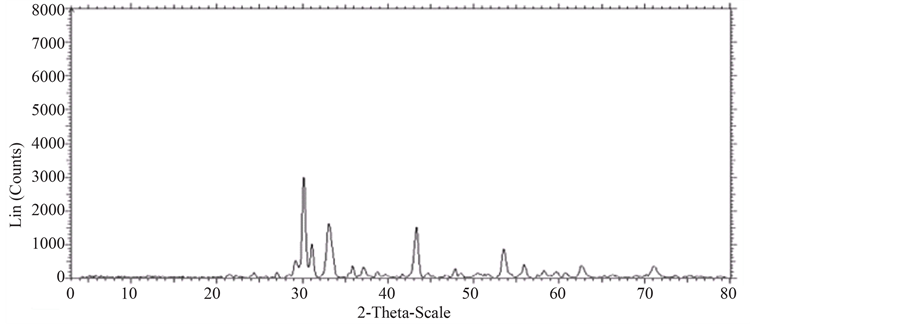
X-ray Diffraction pattern for the three different temperatures in steps for the sample LaZrYBaCaCuO was taken using Bruker AXS D8 advance diffractometer (Figure 2). The diffractometer with radiations of wavelength 1.54184Å having Nickel filter, equipped with X-ray generator 1140/90/96 having X-ray source KRISTALLOFLXE 780,KF,4KE with wide angle goniometer PW1710/70 with single pen recorder pm 8203 and channel control PW1390 at 35 kV, 10 mA is used for the purpose. The scanning speed of the specimen is 2

Figure 1. Structure of LaZrYBaCaCuO.
 (a)
(a) (b)
(b)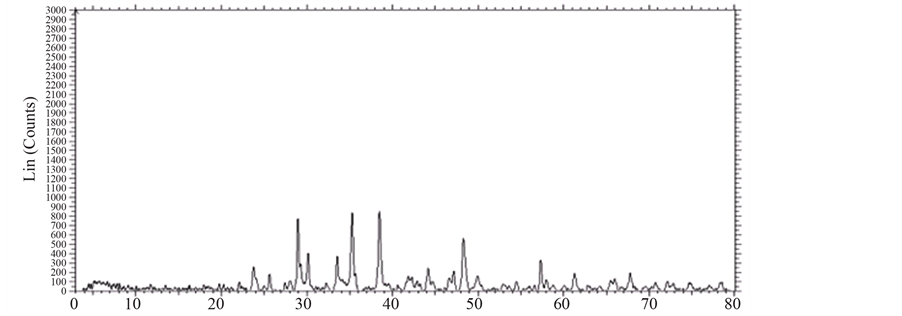 (c)
(c)
Figure 2. XRD of LaZrYBaCa2Cu3O11 at temperatures—(a) 30˚C, (b) 500˚C and (c) 950˚C.
degree/minute. From the XRD results, the obtained d values matching with the JCPDS (Joint Committee on Powder Diffraction Standards) file values. So that it can be concluded that this crystal is found to be orthorhombic system: a = 3.816, b = 3.711, c = 11.826 α = β = γ = 90˚.
From the XRD data, we can calculate the particle size of LaZrYBaCaCuO by using Debye Scherrer equation. Here the authors studied the change of XRD spectrum of LaZrYBaCaCuO at different treating temperatures.
2.2. Particle Size Measurements
Crystal structures are solved by analyzing the intensities of diffracted X-ray beams. X-ray diffraction profile may be used to measure the average crystal size in the sample provided the average diameter is less than 200Å. The lines in a powder diffraction pattern are of finite breadth but if the particles are very small, the lines are broaden than usual. The broadening decreases with the increase in particle size. The particle size for LaZrYBaCaCuO was calculated from X-ray diffraction profiles of strong reflections with intensity % by measuring the full width at half maximum (FWHM). The Debye Scherrer equation for calculating the particle size is given by [1] .

where K is the Scherrer constant, λ is the wavelength of light used for the diffraction, β is the ‘full width at half maximum’ of the sharp peaks, and θ is the angle measured. The Scherrer constant (K) in the above formula accounts for the shape of the particle and is generally taken to have the value 0.9. The results reveal that the particle size .The particle sizes of LaZrYBaCaCuO of different temperature are shown in the Table 1.
2.3. XRD-Instrumental Broadening
When particle size is less than 100 nm, appreciable broadening in X-ray diffraction lines will occur. Diffraction pattern will show broadening because of particle size and strain. The observed line broadening will be used to estimate the average size of the particles. The total broadening of the diffraction peak is due to sample and the instrument. The sample broadening is described by

The total broadening βt equation is described by

where D is average particle size, e is strain and β0 is instrumental broadening. Instrumental broadening is presented in Figure 3.
Table 1. The particle size of LaZrYBaCaCuO at different temperatures, calculated by Debye Scherrer formula.

Figure 3. Typical instrumental broadening.
2.4. Williamson-Hall Plot
This method is attributed to G. K. Williamson and his student, W. H. Hall. It relies on the principle that the approximate formulae for size broadening, βL, and strain broadening, βe, vary quite differently with respect to Bragg angle, θ. Williamson and Hall proposed a method for deconvoluting size and strain broadening by looking at the peak width as a function of 2θ [2] .
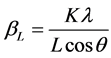
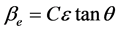
One contribution varies as 1/cosθ and the other as tanθ. If both contributions are present then their combined effect should be determined by convolution. The simplification of Williamson and Hall is to assume the convolution is either a simple sum or sum of squares. Using the former equations, we get:

If we multiply this equation by cosθ we get:

and comparing this to the standard equation for a straight line (m = slope; c = intercept) y = mx + c.
We see that by plotting βtot cosθ versus sinθ we obtain the strain component from the slope (Cε) and the size component from the intercept (Kλ/L). Such a plot is known as a Williamson-Hall Plot. However the Williamson-Hall method has many assumptions: its absolute values should not be taken too seriously but it can be a useful method if used in the relative sense; for example a study of many powder patterns of the same chemical compound, but synthesized under different conditions, might reveal trends in the crystallite size/strain which in turn can be related to the properties of the product. Figure 4 shows Williamson Hall Plot.
2.5. SEM Analysis
Morphology has been analyzed from Scanning Electron Microscope (SEM).The SEM analyses the surface of solid objects, producing images of higher resolution than optical microscopy. It produces representations of three dimensional samples from a diverse range of materials. Figure 5 is the surface morphology of LaZrYBaCaCuO at 950˚C. The particle size measurement through SEM reveals its maximum dimensions always less than 100 nm.
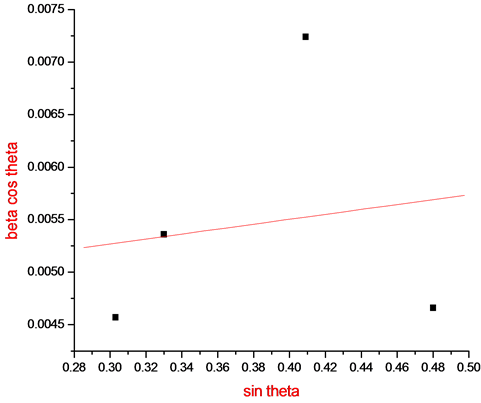
Figure 4. Williamson Hall plot.

Figure 5. SEM photograph of LaZrBaCa2Cu3O11.
2.6. Energy Dispersed X-Ray Spectrograph (EDX)
EDX (Figure 6) shows the composition details of the prepared ceramic powder at 950˚C. The instrument used for this measurement is ISIS Link Oxford Instrument UK. This technique generally associated with Scanning Electron Microscope (SEM). In this technique an electron beam of 10 - 20 KeV strikes the surface of a sample which causes X-ray to be emitted from point of incidence. The energy of the X-ray emitted depends on material under examination. The energy of the characteristic X-ray emitted from the different elements is different and thus it gives the unavoidable signature of the particular element. When an X-ray strikes the detector, it will generate a photoelectron which in turn generates electron-hole pairs. A strong electric field attracts the electrons and holes towards the opposite ends of the detector. The size of the pulse thus generated depends on the number electron-hole pairs created, which in turn depends on the energy of the incoming X-ray. In this method however elements with low atomic number are difficult to be detected. The detector which is Lithium doped Silicon (SiLi) is protected by a Beryllium window and operated at liquid Nitrogen temperatures. The absorption of the soft X-rays by the Beryllium decreases the sensitivity below an atomic number of 11.
3. Results and Discussion
The XRD patterns of LaZrYBaCaCuO powder obtained for various annealing temperatures are shown in Figure 2. XRD spectrum for the different temperatures gave a clear idea about the maximum intensity peak shifting corresponds to the different treating temperatures. And also get the maximum intensity peak difference. The temperature increases, the highest peaks in the XRD spectrums shifts from left to right through the 2θ axis and the highest intensity peak decreases.
The atoms undergo thermal vibration about their mean positions even at the absolute zero of temperature, and the amplitude of this vibration increases as the temperature increases. Increased thermal vibration of the atoms, as the result of an increase in temperature, the unit cell expands, causing changes in plane spacing d and therefore in the 2θ positions of the diffraction lines. And also the intensities of the diffraction lines decrease.
When a material heated from room temperature to high temperature, the amplitude of the thermal vibrations increased. The amplitude is very higher than that at room temperature. After heating, the material cooled to room temperature. The amplitude of the atomic vibrations of the material was decreased. But it couldn’t arrive at the initial amplitude. The atomic vibration amplitude of the heated material was higher than initial amplitude. That means, the atomic vibration amplitude increases, the intensity of the diffracted beam also decreases because it has the effect of smearing out lattice planes. Thus the reinforcement of waves scattered at the Bragg angle by various parallel planes is not as perfect as it is for a crystal with fixed atoms. This reinforcement requires that the path difference, which is a function of the plane spacing d, between waves scattered by adjacent planes be an integral number of wavelengths. The thickness of the planes is 2u, where u is the average displacement of an atom from its mean position. Under these conditions reinforcement is no longer perfect, and it becomes more imperfect as the ratio u/d increases, i.e., as the temperature increases since that increases u, or as θ increases,

Figure 6. EDX of LaZrBaCa2Cu3O11.
since high-θ reflections involve planes of low d value. Thus the intensity of a diffracted beam decreases as the temperature is raised. In intensity calculations, the temperature factor e−2M decreases as 2θ increases [3] .
From Figure 2, the peak broadening in the XRD patterns clearly indicated the nature of the very small nanocrystals. From the width of the XRD peak, the mean crystalline size can be calculated using Debye Scherrer’s equation. From Table 1, particle size of the material LaZrYBaCaCuO increases with respect to the treating temperature increasing. And also it is realized that, θ increases with temperature. The results revealed that the particle size is less than 100 nm. The diffraction data revealed that the material belongs to orthorhombic symmetry. The results were compared with JCPDS data.
Heat treatment causes the particles to anneal and form larger grains, which of course indicates that the particles become larger. Hence, the large particle size of sample at 950˚C is expected. This also agrees with the higher crystallinity, as having larger grains means more long-range order, and hence more crystallinity [4] [5] .
Figure 5 shows SEM image of LaZrYBaCaCuO. The SEM photograph revealed maximum dimensions of the particles to be always less than 100 nm. This is an experimental proof of the theoretical calculation of particle size by Debye Scherrer equation from XRD data.
EDX spectrum of LaZrYBaCaCuO gave the information on the elemental composition of the material. The elemental compositions agree with the stoichiometric relations of the prepared compound. The EDX spectrums obtained (Figure 6) give the material under investigation at 950˚C.
From the EDX spectrum, the six dominant peak positions at, 8 - 9 kev, 5 - 6 kev, 3 - 4 kev, 2 - 1.5 kev, 5 - 1 kev, 0.277 kev, 0.1 - 0.5 kev, correspond quite well to the energy pattern of the corresponding materials (Cu, Ba, Ca, Y, La Zr and O) reported in the EDAX international chart, giving the evidence that La Y& Cu are dominant in LaZrYBaCaCuO samples. Table 2, shows the percentage of the elements in the prepared LaZrYBaCaCuO sample.
The size and strain of the experimentally observed broadening of several peaks are computed simultaneously using least squares method. When, particle size becomes smaller, due to size effect, the peaks become broad and widths larger. The broadening of peak may also occur due to micro strains of the crystal structure arising from defects like dislocation and twinning [6] .
Here, Williamson-Hall plot is plotted with sin θ on the x-axis and βcosθ on the y-axis (in radians). A linear fit is got for the data. From this fit, particle size and strain are extracted from y-intercept and slope respectively. The extracted particle size is 26.54 nm and strain is 0.00234 from Williamson Hall Plot (Figure 4).
4. Conclusion
In this work LaZrYBaCaCuO ceramics were prepared successfully by the conventional solid state reaction tech
Table 2. Material content (EDX).
nique and studied by XRD, SEM, EDX, and particle size measurement. XRD data confirmed the formation of the perovskite phase structure and the average particle size. The XRD spectrums of the LaZrYBaCaCuO at different temperatures indicate that, according to increasing treating temperature, the θ value and particle size also increases. From SEM analysis, the morphology images show the approximate size of the nano particles. The value of particle size calculated from the Williamson-Hall plot method is in agreement with that of the particle size measured from Debye Scherrer formula. The EDX analysis indicates that the elements existing in the sample and it agree with the stoichiometric relations of the prepared compound.
Acknowledgements
The authors are thankful to Kerala State Council For Science, Technology And Environment (KSCSTE), Thiruvanathapuram for granting the financial assistance, SAIF, Kochi for providing the data analysis and to the Principal, CMS College, Kottayam, Kerala for providing the facilities.
References
- West, A.R. (1974) Solid State Chemistry and Its Applications. Wiley, New York.
- Williamson, G.K. and Hall, W.H. (1953) X-Ray Line Broadening from Filed Aluminium and Wolfram. Acta Metallurgica, 1, 22-31. http://dx.doi.org/10.1016/0001-6160(53)90006-6
- Cullity, B.D. (1978) Elements of X-Ray Diffraction. 2nd Edition, Addison-Wesley Publishing Company Inc., Phillippines.
- Xie, Q. and McCourt, F. (2008) Nanotechnology Engineering NE 320L Lab Manual. University of Waterloo, Waterloo, 35-39.
- So, W.W., Jang, J.S., Rhee, Y.W., Kim, K.J. and Moon, S.J. (2001) Preparation of Nanosized Crystalline CdS Particles by the Hydrothermal Treatment. Journal of Colloid and Interface Science, 237, 136-141. http://dx.doi.org/10.1006/jcis.2001.7489
NOTES

*Corresponding author.


