World Journal of Engineering and Technology
Vol.05 No.04(2017), Article ID:79547,11 pages
10.4236/wjet.2017.54B006
Standardization of the Main Dimensions of Design Container Ships in Ports―A Case Study
Soheil Radfar, Amir Taherkhani, Roozbeh Panahi*
Department of Marine Structures, Tarbiat Modares University, Tehran, Iran




Received: August 30, 2017; Accepted: October 9, 2017; Published: October 12, 2017
ABSTRACT
Ports are crucial element in the export and import chains of each country. Therefore, sufficient and efficient designing of ports is of great importance to increase the safety of operations and to lower the construction costs. Their design procedure is iterative and specifications of the design ship are of the most important inputs in this regard. The design ship is characterized with its length (L), breadth (B), and draft (d). In this research a regression analysis has been carried out in the southern coasts of Iran (Persian Gulf) to obtain these specifications. The results have shown under- and over-estimations of the main dimensions. Hence, this supports the idea that it is worth performing individual regression analysis, especially in restricted waterways and in the regions with specific fleet for the sake of verification of recommended values by standard technical guidelines.
Keywords:
Length, Breadth, Draft, Dead Weight Tonnage, Terminal

1. Introduction
A port complex consists of many elements including quays, breakwaters, turning basins, berthing structures, and mooring facilities. Design process of these elements is an iterative procedure. An important parameter in this regard is the correct determination of the capacity and the main dimensions of the design ship that utilizes port facilities [1] [2] [3].
A design ship is characterized by its length (L), breadth (B) and draft (d) as its main dimensions as well as its Dead Weight Tonnage (DWT) or Gross Registered Tonnage (GRT). In the design guidelines and technical standards it is common to present formulae and design charts based on the correlation between DWT/GRT with L, B and D.
To determine the main characteristics of the design ship, a statistical analysis; known as regression analysis is needed. Required data for such analysis may be gathered from many sources e.g. port authorities, governmental organizations, classification societies and global ship tracking databases.
Over the past two decades, Japanese were the pioneers of these analyses for local and global purposes. First serious study on the main dimensions was carried out by Port and Harbor Research Institute (PHRI) in Japan [4]. They utilized Japanese port data and fitted formulae for the design purposes of their port facilities. Later, Akakura and Takahashi [4] in order the generalization of formulae for all over the world, utilized 1-year data (1995-1996) from Lloyd’s Register of Ships and performed a regression analysis on the main dimensions of the design ship. This fundamental research is the basis of some latter guidelines e.g. [5], [6] and [7]. Using this approach, Takahashi et al. [2] based on 1-month data from LMIU1 Shipping Data (January of 2004) and 1-year data from Japanese Register of Ships (2004) conducted regression analysis on nine distinct ship types. This research was later became the reference of Technical Standards and Commentaries of Port and Harbor Facilities [8].
1Lloyd’s List Intelligence (formerly LMIU).
Since the results of previous studies and hence available guidelines and technical standards, propose formulae for all over the world and have general nature, it is worth performing individual regression analyses in each country and local ports. Overestimation of the main dimensions increases the final cost of the port construction/development, and conversely, under estimation of the dimensions would increase the risk accidents, port failures and low efficiency operations. Accordingly, in current research a regression analysis has been carried out in the southern coasts of Iran (Persian Gulf).
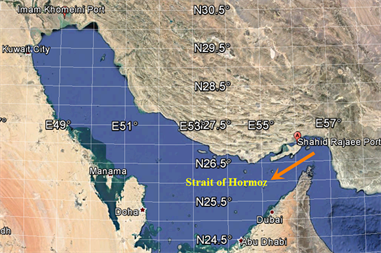
Figure 1 shows the area of interest in this study. It begins with Strait of Hormoz in the east and ends with Khowr-e-Musa in the west side and contains largest (Shahid Rajaei Port) and second largest (Imam Khomeini Port) ports of Iran.
Figure 1. Area of study in the southern coasts of Iran.
Overall throughput of these ports is 76,246,210 and 42,931,757 tons, respectively [9].
This study is structured as follows: in Section 2, methods of statistical analysis have been described and materials of the research are defined. In Section 3.1, the regression analysis has been performed on the available data for container ships and the results are presented. In Section 3.2, obtained results are compared against the results from [5], [6] and [8], and their differences have been specified. Finally, in Section 4, the main conclusions of performed study have been presented.
2. Materials and Methods
2.1. Data
The data used for statistical analysis in this research have been provided by Port and Maritime Organization of Iran (PMO). The data include information such as IMO number, ship name, DWT, GRT, length overall, breadth molded and full load draft for ships calling the Iranian ports of the Persian Gulf since 1999 (17-year data). Total port calls for container ships in the analysis is 985.
2.2. Data Validation
For any statistical analysis it is necessary to evaluate the correctness of available data. To remove/reduce noise and errors from recorded data, “Data filtration” is needed [10]. Here, filtration is performed in two distinct steps. At first, main dimensions of ships are checked with an international source [11] using their IMO number and name. This resulted in 2% of elimination in raw data. Then, due to diversity of data, a standard deviation analysis is performed to exclude out of range data. It yielded into 19% data removal.
2.3. Analysis Methods
As it is mentioned earlier, it is common to demonstrate the main specifications of the design ship in the form of formulae and design charts, which correlate L, B, and D with DWT. This is possible using so called the regression analysis. There are three main technics to perform such analysis:
2.3.1. Logarithmic Regression Analysis Method
According to this method, relationship between main specifications (L, B, D and GRT) of the design ship with its DWT is outlined in the following form:
(1)
here, Y is L, B, D of the specific ship, and X is DWT of the ship.
Applying a logarithm on both sides of Equation (1), it transforms to the following equation:
(2)
This linear regression equation simplifies applying of coverage rate (will be discussed in Section 2.4) on available dat.
2.3.2. Linear Regression Analysis Method
In this method, relationship between main specifications (L, B, D and GRT) of the design ship with its DWT obeys a normal straight line in the form of Equation (3):
(3)
here, Y and X are as before and a, b are constants.
2.3.3. Average Value Analysis Method
In cases where a ship specification is constant regardless of the change in DWT, the average value of the data is calculated as 50% value (a single constant line parallel to DWT-axis). A representative example of this case is the B-DWT relationship for container ships. This happens due to limited breadth for traveling ships in the Panama Canal.
2.4. Coverage Rate
For a specific port it is possible that about 50% of called ships can have bigger dimensions than design values. So, port authorities must be aware of considering safety studies as necessary for the ship with greater dimensions. As it is obvious, increasing the confidence limit will raise the cost of improving port facilities to focus on high service levels. In this study, regression equations according to coverage rates equal to 50%, 75%, and 90% have been set. Here, it is assumed that the distribution of data around the regression equations obeys a normal distribution. This assumption causes a parallel translation form the regression equation of the average value will be obtained from based on the value of conditional standard deviation. The amount of this parallel translation is K*σ; known as conditional standard deviation (CSD) [12].
2.5. Performance Indicators
In the statistical analysis, it is necessary to compare obtained results with those available. This is possible using statistical indices. In this study, coefficient of determination (R2) has been calculated for this purpose [2]. Closer the R2 value to one, the better the proposed results are.
3. Results and Discussion
3.1. Analysis on the Main Specifications of Design Container Ship
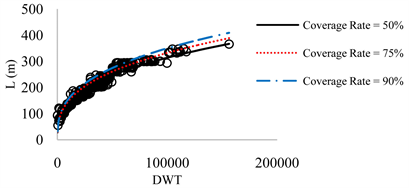
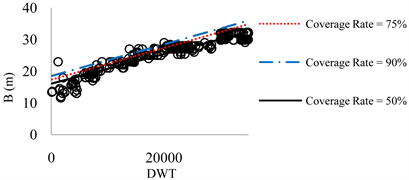
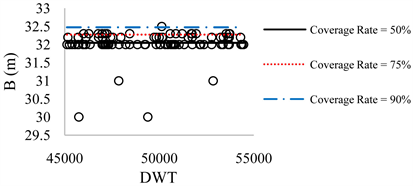
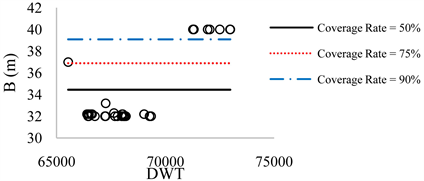
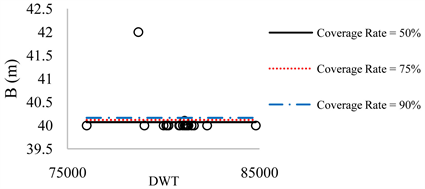
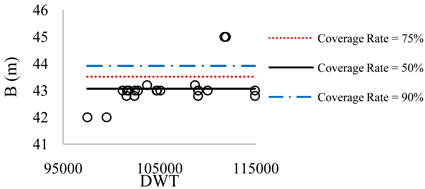
According to three above mentioned methods, the regression analysis has been performed. Results indicate that for the container ships that logarithmic method presents the best results for L value with R2 = 91.6%. For B and D, due to diversity of data it was not possible to fit a single power or linear line on all data. Therefore, total data were broken into seven intervals and the average value method has been used in this regard. The results are presented in Tables 1-4. The results are also presented in Figures 2-9. The figures for D are not presented, here. Table 5 summarizes the overall results for L, B, and D of container ships, and for 50%, 75%, and 90% coverage rate values.
Figure 2. L-DWT.
Figure 3. B-DWT for DWT < 35,000.
Figure 4. B-DWT for 35,000 < DWT < 45,000.
Figure 5. B-DWT for 45,000 < DWT < 55,000.
Figure 6. B-DWT for 55,000 < DWT < 65,000.
Figure 7. B-DWT for 65,000 < DWT < 75,000.
Figure 8. B-DWT for 75,000 < DWT < 85,000.
Figure 9. B-DWT for DWT > 95,000.
Table 1. Relationship between L (m) and DWT for container ships.
Table 2. Relationship between B (m) and DWT (less than 35,000 t) for container ships.
Table 3. Relationship between B (m) and DWT (more than 35,000 t) for container ships.
Table 4. Relationship between D (m) and DWT for container ships.
Table 5. The results of analysis of main specifications of container ships for each coverage rate.
3.2. Comparison with Recommended Values of Guidelines
To assess the new obtained results with corresponding values in guidelines, in this section, the results of statistical analysis are compared against the recommendations of three well-known international guidelines such as ROM [5], Japanese standard [8], and port designer’s handbook [6] for coverage rate of 75%. It should be noted that underestimation of dimensions increase the risks of hazards and overestimation imposes excessive costs on port projects.
3.2.1. ROM vs This Research
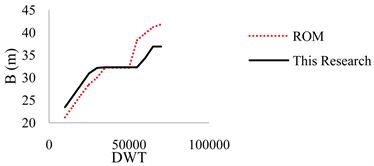
In this section, recommended values of ROM [5] have been compared against the results of current research. Figure 10 shows the results for L. As can be seen, ROM underestimate the length, however the overall correlation is acceptable. Figure 11 shows the results for B. Here, in the midrange results are completely consistent. But, in lower DWTs, ROM underestimates and in the higher DWTs, it overestimates the breadth. The same comparison can be made on D. Table 6 summarizes the quantitative difference between ROM and this research.
Figure 10. Recommended value of L; Comparison between this research with ROM.
Figure 11. Recommended value of B; Comparison between this research with ROM.
Table 6. Comparison between recommended values of the ROM and this research.
3.2.2. Thoresen vs This Research
In this section, recommended values of Thoresen [6] have been compared against the results of current research. Figure 12 shows the results for L. As can be seen, results are completely consistent. Figure 13 shows the results for B. Here, in the midrange results are completely consistent. But, for DWT < 40,000 t, Thoresen underestimates and for DWT > 50,000 t, it overestimates the breadth. The same comparison can be made on D. Table 7 summarizes the quantitative difference between Thoresen and this research.
3.2.3. OCDI vs This Research
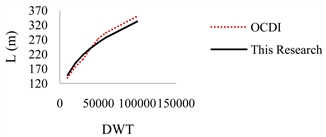
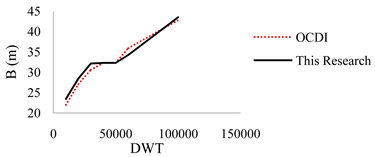
In this section, recommended values of OCDI have been compared against the results of current research. Figure 14 shows the results for L. As L increases, results are spread apart and OCDI overestimates the length. Figure 15 shows the results for B. Here, for DWT > 40,000 t, results are consistent. For lower DWTs, OCDI underestimates the breadth. The same comparison can be made on D. Table 8 summarizes the quantitative difference between OCDI and this research.
Figure 12. Recommended value of L; comparison between this research with Thoresen.
Figure 13. Recommended value of B; comparison between this research with Thoresen.
Figure 14. Recommended value of L; comparison between this research with OCDI.
Figure 15. Recommended value of B; comparison between this research with OCDI.
Table 7. Comparison between recommended values of the Thoresen and this research.
Table 8. Comparison between recommended values of the OCDI and this research.
4. Conclusions
Accurate evaluation of the main dimensions has significant positive effect on final cost and safety of port elements. This study aimed at specifying the main dimensions of design container ships of the southern coasts of Iran. Underestimation of dimensions increases the risks of hazards and overestimation imposes excessive costs on port projects. Detailed comparison of results with recommended values by standard technical guidelines [5], [6], and [8].
As can be seen the under- and over-estimation of results are more evident for B and D. The results for L are almost consistent. This clearly indicates the importance of accurate prediction of ship dimensions in practical and design applications to lower the construction and operational costs of port projects. The results of this research support the idea that it is worth performing individual regression analysis, especially in restricted waterways and in the regions with specific fleet for the sake of verification of recommended values by standard technical guidelines.
Cite this paper
Radfar, S., Taherkhani, A. and Panahi, R. (2017) Standardization of the Main Dimensions of Design Container Ships in Ports―A Case Study. World Journal of Engineering and Technology, 5, 51-61. https://doi.org/10.4236/wjet.2017.54B006
References
- 1. Piko, G.P. (1982) Regression Analysis of Ship Characteristics. Australian Gov-ernment Publishing Service, Australia.
- 2. Takahashi, H., Goto, A. and Abe, M. (2006) Study on Standards for Main Dimensions of the Design Ship. Technical Note of National Institute for Land and Infrastructure Management, Ja-pan.
- 3. Takahashi, H. and Goto, A. (2007) Study on Ship Height by Statistical Analysis. Report of National Institute for Land and Infrastructure Management, Japan.
- 4. OCDI (2009) Technical Standards and Commentaries for Port and Harbour Facilities in Japan. OCDI, Japan.
- 5. Del Estado, P. (1999) Recom-mendations for Maritime Works (Spain) ROM 3.1-99. Designing Maritime Con-figuration of Ports. Approach Channels and Floatation Areas, Spain.
- 6. Thoresen, C.A. (2014) Port Designer’s Handbook. 3rd Edition, ICE Publishing.
- 7. Akakura, Y. and Takahashi, H. (1998) Ship Dimensions of De-sign Ship under Given Confidence Limits. Technical Note of the Port and Har-bour Research Institute, Ministry of Transport, Japan.
- 8. Thoresen, C.A. (2003) Port Designer’s Handbook: Recommendations and Guidelines. Thomas Telford. https://doi.org/10.1680/pdhrag.32286
- 9. PMO (2016) System Operations Statistics year 2016. Ports and Maritime Organization of Iran.
- 10. IGI-Global (2017) What Is Data Filtering. http://www.igi-global.com/dictionary/data-filtering/34068
- 11. MarineTraffic Ship Database. http://www.marinetraffic.com
- 12. Montgomery, J. (2016) Marginal and Conditional Standard Deviation. http://pageswustledu/montgomery/articles/3152