 Materials Sciences and Applicatio ns, 2011, 2, 1383-1391 doi:10.4236/msa.2011.210187 Published Online October 2011 (http://www.SciRP.org/journal/msa) Copyright © 2011 SciRes. MSA 1383 Structure and Bonding of Nanolayered Ternary Phosphides Abdelkader Yakoubi1*, Hanane Mebtouche1, Mohamed Ameri2, Bachir Bouhafs1 1Modeling and Simulation in Materials Science Laboratory, Physics Department, University of Sidi Bel-Abbes, Sidi Bel-Abbes, Al- geria; 2Département de Physique, Faculté des Sciences, Université Djillali Liabès, Sidi-Bel-Abbès, Algeria. Email: *yakoubi_aek@yahoo.fr Received April 2nd, 2011; revised April 25th, 2011; accepted May 25th, 2011. ABSTRACT We have studied the electronic structure and chemical bonding mechanism of nanolayered M2SbP with M = Ti, Zr and Hf using the full-relativistic of an all-electron full potential linearized augmented-plane-wave (FP-LAPW) method based on the density functional theory, within the local density approximation scheme for the exchange-correlation potential. Furthermore, we have to calculate the energy of formation for prove the existence of these compounds experimentally. Geometrical optimizations of the unit cell are in good agreement with the available theoretical and experimental data. The bulk modulus of M2SbP conserved as Ti is replaced with Zr, and increases by 8.7% as Ti is replaced with Hf, which can be understood on the basis of the increased number of valence electrons filling the p-d hybridized bonding states. The bonding is of covalent-ionic nature with the presence of metallic character. Analyzing the bonding in the binary MP, it can be concluded that this character is essentially conserved in M2SbP ternaries. Keywords: Ceramics, Ab-Initio Calculations, Electronic Structure, Crystal Structure, Equations-of-State 1. Introduction Mn+1AXn (MAX) (n = 1 to 3) phases are a series of ce- ramics but with a combination of ductility, conductivity and machinability comparable to metals. M is an early transition metal, A is an A-group element (mostly IIIA and IVA) and X is either C or N. These phases have hexagonal layered structures and belong to the space group P63/mmc, where in Mn+1Xn layers interleaved with pure layers of the A-group elements. The structures of the vast majority of these compounds were determined by Nowotny [1] and co-workers in the sixties. The MAX phases are typical representatives of nano- laminated phases, and according to M. W. Barsoum et al. [2,3], these phase characterized by high elastic moduli, are machinable [4], exhibit good damage tolerance [5], excellent thermal shock resistance [6], and good corro- sion resistance [7], and they are good thermal and elec- trical conductors [4]. This unique combination of proper- ties serves as motivation for fundamental as well as ap- plied research. MAX phases are used as formers for healthcare products, hot pressing tools, and resistance heating elements [8,9], and are suitable for many tech- nological applications. Extensive experimental and theoretical studies were reported on MAX phases because of their special me- chanical, thermal and electrical properties. A. D. Bor- tolozo et al. [10] investigated Ti2InC by x-ray diffraction, magnetic and resistivity measurements. This work sus- tains the idea of the existence of a new class of super- conducting materials that crystallizes in the Cr2AlC pro- totype. T. Scabarozi et al. [11] report on correlations between thermal expansion, elastic modulii, thermal transport, specific heat, and electrical transport measurements of materials within the MAX-phase family. Elastic modulus measurements are made using an ultrasonic time of flight technique. Thermal expansion measurements are made using high-temperature x-ray diffractions. Also, the electronic properties of these materials have been studied both theoretically and experimentally [12]. For MAX-phases in thin film form, the processing and physical properties have been recently reviewed.[13] Because the MAX-phases crystallize in a hexagonal struc- ture the anisotropy of its conductivity is of great interest but it has been difficult to experimentally resolve this issue [14,15]. This design criteria is not only limited to the carbides  Structure and Bonding of Nanolayered Ternary Phosphides 1384 and nitrides ternary, but it can also be found in ternary phosphides crystallize in the same structure. M2SbP (M = Ti, Zr, Hf) compound belong to the MAX phases [2], the Ti2SbP, Zr2SbP, Hf2SbP compound have been less investigated compared to the other mem- bers of this family. Few experimental and theoretical works have been done to investigate their properties. Experimentally, H. Boller [15], synthesized this com- pound by power sintering at 800˚C. Theoretically, D. Music and co-workers [16] investigated the chemical bonding and elastic properties of this compound and the correlation between the electronic structure and elastic properties of nanolaminates ternary phosphides [17] us- ing ab initio calculation. In our paper, we present theoretical results of the bulk modulus and chemical bonding of M2SbP and see the effect of a different transition metals element of IVB group in the electronic properties. The aim of this work is to evaluate the chemical bonding and the bulk modulus of our compounds, as the number of valence electrons in third and fourth periods are increased to gain better insight into this technologically interesting class of materials. 2. Methodology and Computational Details In this present work, the calculations of both crystal op- timization and electronic structures were performed in the WIEN2K package [18]. The Kohn-Sham equations were solved by using the highly accurate all-electron full-potential linearized augmented plane-wave plus local orbitals (FP-L/APW + lo) method [19,20] in the framework of density functional theory (DFT) with the exchange-correlation functional treated in the local den- sity approximations (LDA) using the scheme of Perdew- Wang [21]. This method makes no shape approximation to the potential or the electron density. Within the FP- LAPW method, the unit cell is divided into nonoverlap- ping muffin-tin (MT) spheres and an interstitial region. Inside the muffin-tin sphere of radius RMT, the wave functions are expanded using radial functions (solution to the radial Schrödinger equation) times spherical har- monics up to max, and the expansion of the potential inside the muffin-tin spheres is carried out up to max. The parameter max (MT R is the mallets muffin-tin spherical radius present in the system and max is the truncation of the modulus of the recipro- cal-lattice vector) is used to determine the number of plane waves needed for the expansion of the wave func- tion in the interstitial region, while the parameter Gmax is used to truncate the plane-wave expansion of the poten- tial and density in the interstitial region. Here, the MT radii were set to 2.22, 2.4, and 2.7 a.u. for the Ti, Zr, and Hf atoms, respectively and 2.5, 1.9 a.u. for the Sb and P atoms respectively. Moreover, we let , max wf l Pot l n RK 9.0 min K min MT max R*K 9.0 wf l10 mi MT , max Pot l4 , and max . The separate en- ergy of −6.0 Ry was used between valence and core states. Thus, the Ti: [Ar]3d24s2, Zr: [Kr]4d25s2, and Hf: [Xe]4f145d26s2, were treated as valence states, while Sb: [Kr]4d105s25p3 and P: [Ne]3s23p3 were acted as semicore states with other electrons as core states. The energy level of unoccupied states was calculated until 7.5Ry (Emax = 7.5 Ryd). Integrations in the first Brillouin zone (FBZ) have been performed using the Monkhorst-Pack method [22] with 111 special k points [23]. Self-consis- tency calculation of electronic structures is achieved when the total-energy variation from iteration to iteration converged to a 1 mRyd accuracy or better. G14 In the WIEN2K code, core states were treated at the fully relativistic approximation with including spin-orbit interaction [18] as the spin-orbit coupling (SOC) term in the Hamiltonian for the valence states, HSOC, was treated as a perturbation in the second variationnel method, whereas the Dirac equation was solved for the core states. We compute lattice constants, bulk moduli and the opti- mized free internal parameters by fitting the total energy vs. volume curves to the equation of states [24]. The partial density of states and charge-density distri- butions are obtained using the relaxed structures at the equilibrium volumes. The input lattice parameters of the M2SbP studied are taken from Reference [17] and those of MP in the Hexagonal structure as well as TiSb alloy, which are used for the comparison purposes, can be found in References [34,35]. 3. Results and Discussion 3.1. Equilibrium, Formation of Energy and Cohesive Properties M2SbP (M = Ti, Zr, and Hf) compounds crystallize in the Cr2AlC crystal structure, with space group P63/mmc (#194). Its unit cell contains two formula units, and the atoms occupy the Wyckoff positions 2(a) [(0, 0, 0), (0, 0, 1/2)] for P, 2(d) [(1/3, 2/3, 3/4), (2/3, 1/3, 1/4)] for Sb, and 4(f) [(1/3, 2/3, z), (2/3, 1/3, z + 1/2), (2/3, 1/3, –z), (1/3, 2/3, –z + 1/2)] for M, where z is the internal free coordi- nate. The structure is thus defined by two lattice parame- ters, a and c, and the internal structural parameter, z. The phosphor (P) atoms fill the octahedral locations between the M layers [16,17]. The repeating structure of the planes in the unit cell can be further defined by the APCMBSbCMAPBMCSbBM close-pack stacking along the Z-axis [25-27]. The letters A, B, and C stand for the three distinct positions for atoms to occupy, in the close- packed <0001> plane [29]. The subscripts denote the type of atom that sits at the site, e.g. BM means the metal atom M sits at a B site. The Z-coordinate increases as we go from left to right. Copyright © 2011 SciRes. MSA  Structure and Bonding of Nanolayered Ternary Phosphides Copyright © 2011 SciRes. MSA 1385 parameters and the bulks moduli of M2SbP (they are treated the potential of exchange-correlation by the GGA) [16]. We have first chosen lattice parameters and internal parameters to start calculations. We then vary these pa- rameters until reaching the minimum of energy. On the scale of meV, the energy bands near the energy gap de- pend critically on the structural parameters that are not determined by symmetry. We have therefore performed detailed structural optimizations of the unit cell geome- tries as a function of the external stress by minimizing the total energy. Our results of the calculated lattice con- stants a and c, bulk modulus and its pressure derivative, and the optimized free internal parameters are reported in Table 1. Good agreement between our calculations and experimental data of H. Boller [15] and theoretical data of D. Music et al. [16,17] is obtained. Our calculations are slightly underestimated compared to the experimental values of as commonly observed in LDA calculations. The deviation from the experimental values of c and a for Ti2SbP was 1.03% and 1.65%, respectively. For Zr2SbP, the change from experimental values was 0.76% and 0.79%, while for Hf2SbP it was 0.61% and 0.79%, re- spectively [15]. Although the bulk moduli have not been experimentally measured, but a good agreement is ob- served with the other first principle data for the lattice To study stabilities of relative phase for these pho- sphides hexagonal, we have calculated the energy of formation (Eform) per atom by using the following equa- tion: 2 2 MSbP MSbP MSbP totalsolid solid solid form E 4E2E2E E= 8 (1) where M designates a metal with Ti, Zr and Hf crystal- lizing in the hexagonal structure (space group P63/mmc, prototype Mg) [29-31], Sb is a trigonal structure (space group R3m, prototype αAs) [32], and P crystallize in the triclinic structure (space group P1) [33]. There are two atoms in the unit cell for every metal, the indication of the stability of these compounds with the following values according to these calculations of the energy of formation, for Ti2SbP, Zr2SbP and Hf2SbP are −0.67 eV/atom, −0.79 eV/atom and −0.74 eV/atom respectively, these are listed in Table 2. The cohesive energy is a measure of the strength of the forces that bind atoms together in the solid state and is Table 1. The equilibrium lattice parameters (a, c and c/a), internal parameter (z), bulk modulus (B) and its pressure deriva- tive (B’) for M2SbP with M = Ti, Zr, and Hf. Compounds a (Å) c (Å) c/a z B (GPa) B’ Ti2SbP Present work 3.58 12.42 3.47 0.099 134.6 4.11 Exp [15] 3.64 12.55 3.45 0.100 - - Ref [16] 3.65 12.63 3.46 0.100 115 4.25 Zr2SbP Present work 3.79 13.14 3.47 0.103 134.5 4.24 Exp [15] 3.82 13.24 3.47 0.103 - - Ref [16] 3.84 13.44 3.50 0.103 116 4.30 Hf2SbP Present work 3.76 12.96 3.45 0.102 144.4 4.13 Exp [15] 3.78 13.04 3.45 0.102 - - Ref [16] 3.81 13.21 3.47 0.102 125 4.19 Table 2. The calculated values of the energy of formation (Eform), bulk moduli (B), cohesive energies (Ecoh) and the valence electron concentration (val-el) for M2SbP. Ti2SbP Zr2SbP Hf2SbP Eequilibre (eV) −463670.52774 −762143.63421 −2012635.855 Eform (eV/atom) −0.69 −0.79 −0.74 Ecoh (eV/atom) 12.75 13.25 15.44 B (GPa) 134.6 134.5 144.4 Valence electron 88 88 144 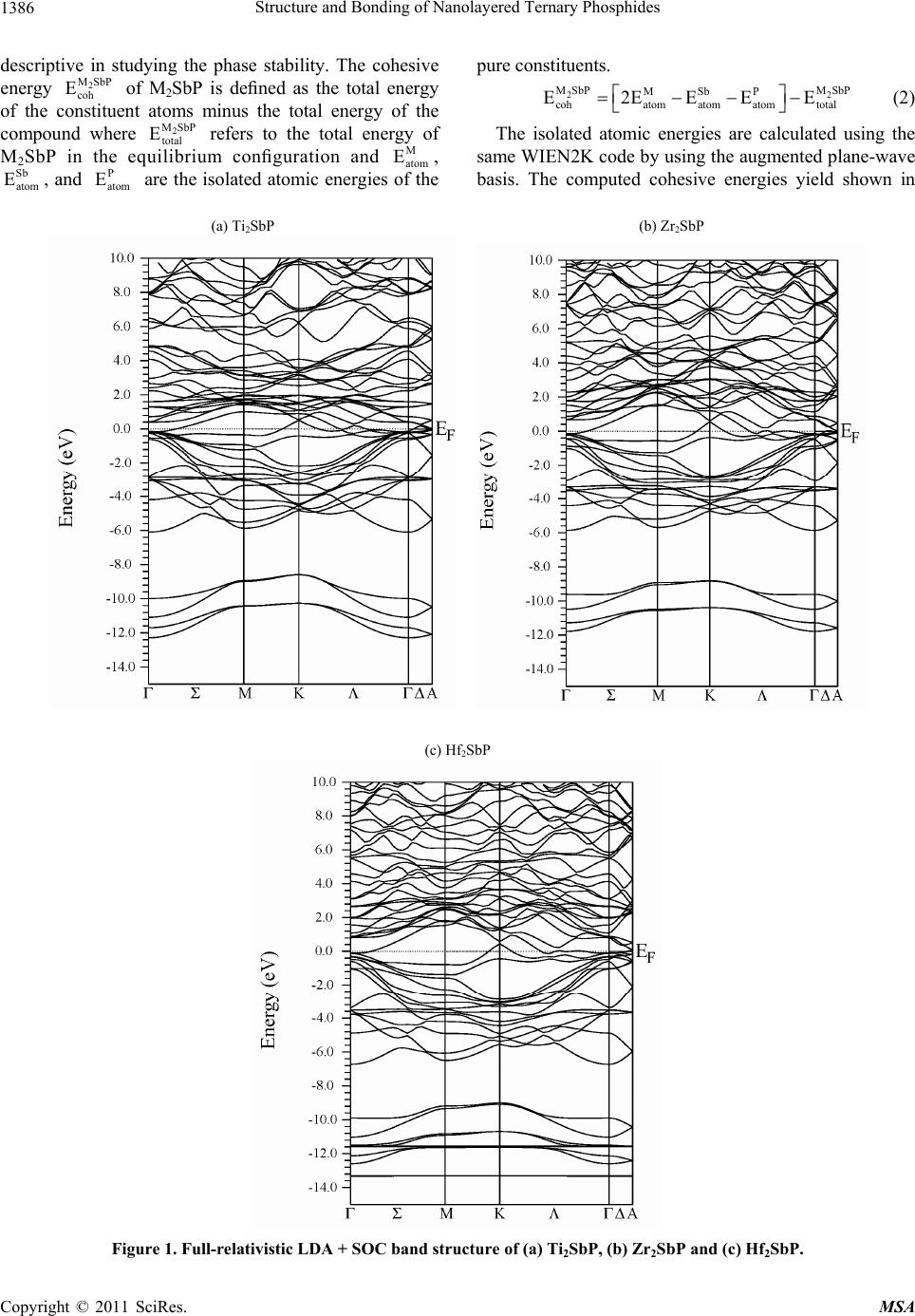 Structure and Bonding of Nanolayered Ternary Phosphides 1386 descriptive in studying the phase stability. The cohesive energy coh of M2SbP is defined as the total energy of the constituent atoms minus the total energy of the compound where total refers to the total energy of M2SbP in the equilibrium configuration and atom , , and are the isolated atomic energies of the 2 MSbP E 2 MSbP E M E Sb atom Eom 22 MSbP MSbP MSbP cohatom atom atomtotal E2EEEE P at E pure constituents. (2) The isolated atomic energies are calculated using the same WIEN2K code by using the augmented plane-wave basis. The computed cohesive energies yield shown in (a) Ti2SbP (b) Zr 2SbP (c) Hf2SbP Figure 1. Full-relativistic LDA + SOC band structur e of (a) Ti2SbP, (b) Zr2SbP and (c) Hf2SbP. Copyright © 2011 SciRes. MSA  Structure and Bonding of Nanolayered Ternary Phosphides1387 Table 2. 12.75 eV/atom for Ti2SbP, 13.25 eV/atom for Zr2SbP, and 15.44 eV/atom for Hf2SbP. It shows that the cohesive energies of the ternary first-column transition- metal phosphides increase monotonously, as in the se- quence Ti2SbP < Zr2SbP < Hf2SbP. The bulk modulus represents the resistance to volume change and is related to the overall atomic binding prop- erties in a material. Therefore, we confirmed in the Table 2, it is expected to change in the same trend of the cohe- sive energy, according to the transition-metal ion (the M element) and the valence electrons population of the M2SbP. 3.2. Band Structures and Density of States We calculated the electronic band structures using the full relativistic effects (including spin-orbit interaction) for Ti2SbP, Zr2SbP, and Hf2SbP are given in Figures 1(a), (b) and (c) respectively, at their equilibrium lattice constants at different high-symmetry points in the Bril- louin zone. The band structures also show strong anisotropic fea- tures with smaller energy dispersion along the c-axis. The valence and conduction bands overlap considerably and there is no band gap at the Fermi level. This finding confirms the metallicity of these materials. The electrical conductivity is anisotropic for this material, i.e. the elec- trical conductivity along the c-axis is much lower than that in the basal planes. The effect of the spin-orbit cou- pling (SOC) is clear in the Hf2SbP compound because the hafnium is a strongly correlated element. The calculated total density of states (TDOS) using the LDA + SOC for M2SbP, where M = Ti, Zr, and Hf are presented in Figure 2. It is apparent that these phases are alike, signifying similarity in chemical bonding. As shown in the figure, the Fermi level of M2SbP is located at a pseudogap between the bonding and nonbonding states. A similar pseudogap is also found in many other MAX phases [34,35]. Generally, a pseudogap correlates to the structure stability [36]. So it is believed that the presence of pseudogap in M2SbP contributed to its phase stability. At the Fermi level Efermi, the DOS for Ti2SbP, Zr2SbP, and Hf2SbP, were 2.12, 1.71 and 1.59 states per unit cell per eV, respectively. Thus there is a small de- creasing trend in the DOS at Efermi with increasing atomic numbers of the transition metal (M). To further elucidate the nature of chemical bonding in these compounds, we study the partial density of states (PDOS) of Ti2SbP, a representative, given in Figure 3(a) Phosphorus does not contribute to the DOS at the Fermi level and therefore is not involved in the conduction properties. Ti d electrons are mainly contributing to the DOS at the Fermi level, and should be involved in the conduction properties. Sb electrons do not contribute significantly at the Fermi level. These results are consis- tent with previous reports on MAX phases [37]. It is evident that a covalent interaction occurs between the constituting elements due to the fact that states are de- generate with respect to both angular momentum and lattice site. P 3p and Ti 3d as well as Sb 4p and Ti 3d states are hybridized. Also, due to the difference in elec- tronegativity between the comprising elements, some ionic character can be expected. The bonding character may be described as a mixture of covalent-ionic and, due to the d resonance in the vicinity of the Fermi level, me- tallic. The pseudogap, common to all M2SbP phases studied (see Figure 2), is likely to split the bonding and antibonding orbitals. This behavior is consistent with previous reports on MAX phases [37-39]. Furthermore, it has been found for Nb3SiC2 [40] that the balanced crystal orbital overlap population analysis [41] is consistent with the PDOS analysis suggesting splitting in PDOS. However, there is also a difference with respect to the role of the A element. In the MAX phases [37,38] the A-M hybridization is weaker than the Sb-M hybridization in the M2SbP phases. At the same time, the chemical bonding between M and X elements Figure 2. Full-relativistic total density of states (TDOS) for M2SbP with (M = Ti, Zr, Hf). Copyright © 2011 SciRes. MSA  Structure and Bonding of Nanolayered Ternary Phosphides 1388 (a) (b) (c) Figure 3. Full-relativistic partial density of states (PDOS) for Ti2SbP, Zr2SbP and Hf2SbP. Copyright © 2011 SciRes. MSA  Structure and Bonding of Nanolayered Ternary Phosphides1389 in the MAX phases and between M and P in the here studied phosphides is rather similar (see Figures 3(a), (b), (c)). 3.3. Charge Densities The high modulus of Ti2SbP can be explained based on bonding characters. To visualize the nature of the bond character and to explain the charge transfer and the bonding properties of the Ti2SbP, Zr2SbP and Hf2SbP compounds, we have investigated the effect of the M states on the total charge densities (see Figure 4). It is known that MAX phases are usually stacks of ‘hard’ M-X bond and “soft” M-A bond along c direction. For example, the Ti-C bond strength is much stronger than Ti-Al bond in Ti2AlC [38]. However, for Ti2SbP (shown in Figure 4(a)), in addition to the Ti-P hybridization (covalent bonding), there is also a strong interaction be- tween Ti and Sb atoms (metallic bonding). This means that the “soft” M-A bond is strengthened in Ti2SbP, which is an extraordinary example in MAX phases stud- ied so far. We believe that this strengthening effect con- tributed considerably to the increase in bulk modulus of Ti2SbP. While the more electropositive nature of Sb confirms the ionic bonding between Ti and Sb. Therefore, the chemical bonding in Ti2SbP is metallic-covalentionic in nature. Figure 4. Electron density distribution of (a) Ti2SbP, (b) Zr2SbP, (c) Hf2SbP, in the (1120) plane. The electron den- sity distribution increases from 0.05 (white) to 15.0 (black) electron/Å3 for Ti2SbP, Zr2SbP, and Hf2SbP. Figure 5 shows the charge-density contours in the plane for Ti2SbP Figure 5(a), as well as in the (1120) (1120) plane for TiP Figure 5(b), where the latter phase crystallizes in hexagonal structure with space group P63/mmc [42]. Analyzing the M-P bonding in TiP, it can be con- cluded that the bonding is characterized by covalent and ionic contributions and that this character is essentially conserved in the M2SbP ternaries. While the charge den- sity distribution of TiP is similar to the one of ZrP and HfP, the charge distribution of the related ternaries shows extensive differences. The coupling between the MP layer and the Sb layer is weaker for Ti2SbP as compared to Zr2SbP and Hf2SbP. In fact, the bonding between Ti and Sb in Ti2SbP is similar to the bonding in TiSb (space group Cmcm) [43], as can be seen in Figure 5(c). Hence, the structure electronic data presented in Figure 2 can be understood based on the charge density data discussed here. These findings provide a pathway for tailoring the electronic properties of M2SbP by tuning the valence electron population. As the valence electron population of the transition metal M is increased, more charge is placed in the M-P bonds, which is due to an increase in the P p-M d hybridization as can be seen in Figure 2, where the partial density of states data are presented for Ti2SbP (Figure 3(a)), Zr2SbP (Figure 3(b)), and Hf2SbP (Figure 3(c)). Figure 5. Contour plot of the total valence charge densities for (a) Ti2SbP and (b) TiP in the (112 0 ) pla ne, and (c) TiSb in the (100) plane. 4. Conclusions In summary we have studied the electronic structure and chemical bonding of M2SbP compounds with (M = Ti, Zr and Hf), by means of ab initio calculations using the full potential linearized augmented-plane-wave (FP-LAPW) method. The bulk modulus conserved as Ti is replaced with Zr, and increases by 8.7% as Ti is replaced with Hf. Copyright © 2011 SciRes. MSA  Structure and Bonding of Nanolayered Ternary Phosphides 1390 This can be understood since the substitution is associ- ated with an increased valence electron concentration, resulting in band filling and an extensive increase in co- hesion. To study stabilities of relative phase for these phosphides hexagonal, we have calculated the energy of formation (Eform) per atom. The energy of formation in- dicates that these materials do form. This work is important for basic understanding of structure and bonding of these phases and may encourage future experimental research. 5. Acknowledgements One of us (B. B.) acknowledges the Abdus-Salam Inter- national Center for Theoretical Physics (Trieste-Italy). REFERENCES [1] H. Nowotny, “Strukturchemie Einiger Verbindungen der Ubergangsmetalle mit den Elementen C, Si, Ge, Sn,” Pro- gress in Solid State Chemistry, Vol. 5, 1971, pp. 27-70. [2] M. W. Barsoum, “The MN+1AXN Phases: A New Class of Solids: Thermodynamically Stable Nanolaminates,” Pro- gress in Solid State Chemistry, Vol. 28, No. 1-4, 2000, pp. 201-281. doi:10.1016/S0079-6786(00)00006-6 [3] M. W. Barsoum and T. El-Raghy, “The MAX Phases: Unique New Carbide and Nitride Materials,” American Scientist, Vol. 89, No. 4, 2001, pp. 336-345. [4] M. W. Barsoum and T. El-Raghy, “Synthesis and Chara- cterization of a Remarkable Ceramic: Ti3SiC2,” Journal of the American Ceramic Society, Vol. 79, No. 7, 1996, pp. 1953-1956. doi:10.1111/j.1151-2916.1996.tb08018.x [5] M. W. Barsoum, T. El-Raghy and L. U. J. T. Ogbuji, “Oxidation of Ti3SiC2 in Air,” Journal of the Electro- chemical Society, Vol. 144, No. 7, 1997, pp. 2508-2516. doi:10.1149/1.1837846 [6] T. El-Raghy, et al., “Processing and Mechanical Proper- ties of Ti3SiC2: II. Effect of Grain Size and Deformation Temperature,” Journal of the American Ceramic Society, Vol. 82, No. 10, 1999, pp. 2855-2860. [7] Z. Sun, Y. Zhou, and M. Li, “Oxidation Behaviour of Ti3SiC2-Based Ceramic at 900˚C - 1300˚C in Air,” Cor- rosion Science, Vol. 43, No. 6, 2001, pp. 1095-1109. doi:10.1016/S0010-938X(00)00142-6 [8] “MAXTHAL Data Sheet,” 3-One-2 LLC, Voorhees, New Jersey. http://www.3one2.com [9] “Globar Bulk Ceramic Non-Inductive Resistors,” Kanthal, an affiliate of Sandvic AB, Sandviken, Sweden. http://www.kanthal.com [10] A. D. Bortolozo, O. H. Sant’Anna, C. A. M. dos Santos and A. J. S. Machado, “Superconductivity in the Hex- agonal-Layered Nanolaminates Ti2InC Compound,” Solid State Communications, Vol. 144, No. 10-11, 2007, pp. 419- 421. doi:10.1016/j.ssc.2007.09.028 [11] T. H. Scabarozi, S. Amini, P. Finkel, O. D. Leaffer, J. E. Spanier, M. W. Barsoum, M. Drulis, H. Drulis, W. M. Tambussi, J. D. Hettinger and S. E. Lofland, “Electrical, Thermal, and Elastic Properties of the MAX-Phase Ti2SC,” Journal of Applied Physics, Vol. 104, No. 3, 2008, pp. 3502-3506. doi:10.1063/1.2959738 [12] M. Magnuson, M. Mattesini, S. Li, C. Höglund, M. Beck- ers, L. Hultman and O. Eriksson, “Bonding Mechanism in the Nitrides Ti2AlN and TiN: An Experimental and Theo- retical Investigation,” Physical Review B, Vol. 76, No. 19, 2007, pp. 5127-5135. doi:10.1103/PhysRevB.76.195127 [13] V. Mauchamp, G. Hug, M. Bugnet, T. Cabioc’h and M. Jaouen, “Anisotropy of Ti2AlN Dielectric Response In- vestigated by ab Initio Calculations and Electron En- ergy-Loss Spectroscopy,” Physical Review B, Vol. 81, No. 3, 2010, pp. 5109-5116. doi:10.1103/PhysRevB.81.035109 [14] N. Haddad, E. Garcia-Caurel, L. Hultman, M. W. Bar- soum and G. Hug, “Dielectric Properties of Ti2AlC and Ti2AlN MAX Phases: The Conductivity Anisotropy,” Journal of Applied Physics, Vol. 104, No. 2, 2008, pp. 3531-3540. doi:10.1063/1.2960340 [15] H. Boller, “Gemischte Pnictide Mit Geordnetem TiP-Typ (Ti2SC-Typ),” Monatshefte für Chemie, Vol. 104, No. 1, 1973, pp. 166-171. doi:10.1007/BF00911157 [16] D. Music, Z. Sun, and J. M. Schneider, “Structure and Bonding of M2SbP (M = Ti, Zr, Hf),” Physical Review B, Vol. 71, No. 9, 2005, pp. 2102-2104. doi:10.1103/PhysRevB.71.092102 [17] D. Music and J. M. Schneider, “The Correlation between the Electronic Structure and Elastic Properties of Nano- laminates,” Journal of the Minerals, Metals and Materi- als Society, Vol. 59, No. 7, 2007, pp. 60-64. [18] P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, “WIEN2k: An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties,” Technische Universität Wien, Vienna, 2001. [19] G. K. H. Madsen, P. Blaha, K. Schwarz, E. Sjöstedt and L. Nordström, “Efficient Linearization of the Augmented Plane-Wave Method,” Physical Review B, Vol. 64, No. 19, 2001, pp. 5134-5143. doi:10.1103/PhysRevB.64.195134 [20] K. Schwarz, P. Blaha and G. K. H. Madsen, “Electronic Structure Calculations of Solids Using the WIEN2k Pack- Age for Material Sciences,” Computer Physics Communi- cations, Vol. 147, No. 1-2, 2002, pp. 71-76. doi:10.1016/S0010-4655(02)00206-0 [21] J. P. Perdew and Y. Wang, “Accurate and Simple Ana- lytic Representation of the Electron-Gas Correlation En- ergy,” Physical Review B, Vol. 45, No. 23, 1992, pp. 13244-13249. doi:10.1103/PhysRevB.45.13244 [22] H. J. Monkhorst and J. D. Pack, “Special Points for Bril- louin-Zone Integrations,” Physical Review B, Vol. 13, No. 12, 1976, pp. 5188-5192. doi:10.1103/PhysRevB.13.5188 [23] P. E. Blöchl, O. Jepsen and O. K. Andersen, “Improved Tetrahedron Method for Brillouin-Zone Integrations,” Phy- sical Review B, Vol. 49, No. 23, 1994, pp. 16223-16233. [24] F. D. Murnaghan, “The Compressibility of Media under Copyright © 2011 SciRes. MSA  Structure and Bonding of Nanolayered Ternary Phosphides1391 Extreme Pressures,” Proceedings of the National Acad- emy of Sciences of the USA, Vol. 30, No. 9, 1944, pp. 244-247. doi:10.1073/pnas.30.9.244 [25] Naval Research Laboratory Center for Computational Materials Science, “Structures in a Hexagonal Space Group (#168-#194),” 2002. http://cst-www.nrl.navy.mil/lattice/spcgrp/hexagonal.html #sg194 [26] G. Hug, M. Jaouen and M. W. Barsoum, “X-Ray Absorp- tion Spectroscopy, EELS, and Full-Potential Augmented Plane Wave Study of the Electronic Structure of Ti2AlC, Ti2AlN, Nb2AlC, and (Ti0.5Nb 0.5)2AlC,” Physical Review B, Vol. 71, No. 2, 2005, pp. 4105-4116. doi:10.1103/PhysRevB.71.024105 [27] G. Hug and E. Fries, “Full-Potential Electronic Structure of Ti2AlC and Ti2AlN,” Physical Review B, Vol. 65, No. 11, 2002, pp. 3104-3107. doi:10.1103/PhysRevB.65.113104 [28] N. W. Ashcroft and N. D. Mermin, “Crystal Lattices,” Solid State Physics, Chapter 4, Brooks/Cole, Belmont, 1976, pp. 64-83. [29] R. R. Pawar and V. T. Deshpande, “The Anisotropy of the Thermal Expansion of α-Titanium,” Acta Crystallogra- phica, Vol. A24, Part 2, 1968, pp. 316-317. doi:10.1107/S0567739468000525 [30] B. Olinger and J. C. Jamieson, “Zirconium: Phases and Compressibility to 120 Kilobars,” High Temperatures- High Pressures, Vol. 5, No. 2, 1973, pp. 123-131. [31] R. Russell, “On the Zr-Hf System,” Journal of Applied Physics, Vol. 24, No. 2, 1952, pp. 232-233. [32] D. Schiferl, “50-Kilobar Gasketed Diamond Anvil Cell for Single-Crystal X-Ray Diffractometer Use with the Crystal Structure of Sb up to 26 Kilobars as a Test Prob- lem,” Review of Scientific Instruments, Vol. 48, No. 1, 1977, pp. 24-30. doi:10.1063/1.1134861 [33] A. Simon, H. Borrmann and H. Craubner, “Crystal Struc- ture of Ordered White Phosphorus (β-P),” Phosphorus and Sulfur and the Related Elements, Vol. 30, No. 1-2, 1987, pp. 507-510. doi:10.1080/03086648708080631 [34] G. Hug and E. Fries, “Full-Potential Electronic Structure of Ti2AlC and Ti2AlN,” Physical Review B, Vol. 65, No. 11, 2002, pp. 3104-3107. doi:10.1103/PhysRevB.65.113104 [35] T. Liao, J. Y. Wang and Y. C. Zhou, “Superior Mechani- cal Properties of Nb2AsC to Those of Other Layered Ter- nary Carbides: A First-Principles Study,” Journal of Phy- sics: Condensed Matter, Vol. 18, No. 41, 2006, pp. L527- L533. doi:10.1088/0953-8984/18/41/L04 [36] J. H. Xu and A. J. Freeman, “Band Filling and Structural Stability of Cubic Trialuminides: YAl3, ZrAl3, and NbAl3,” Physical Review B, Vol. 40, No. 17, 1989, pp. 11927- 11930. doi:10.1103/PhysRevB.40.11927 [37] J. Wang and Y. Zhou, “Dependence of Elastic Stiffness on Electronic Band Structure of Nanolaminate M2AlC (M = Ti, V, Nb, and Cr) Ceramics,” Physical Review B, Vol. 69, No. 21, 2004, pp. 4111-4120. doi:10.1103/PhysRevB.69.214111 [38] Z. Sun, D. Music, R. Ahuja, S. Li and J. M. Schneider, “Bonding and Classification of Nanolayered Ternary Carbides,” Physical Review B, Vol. 70, No. 9, 2004, pp. 092102-092104. doi:10.1103/PhysRevB.70.092102 [39] Z. Sun, R. Ahuja, S. Li and J. M. Schneider, “Structure and Bulk Modulus of M2AlC (M = Ti, V, and Cr),” Ap- plied Physics Letters, Vol. 83, No. 5, 2003, pp. 899-871. doi:10.1063/1.1599038 [40] A. Grechnev, S. Li, R. Ahuja, O. Eriksson, U. Jansson and O. Wilhelmsson, “Layered Compound Nb3SiC2 Pre- dicted from First-Principles Theory,” Applied Physics Letters, Vol. 85, No. 15, 2004, pp. 3071-3073. doi:10.1063/1.1791734 [41] A. Grechnev, R. Ahuja and O. Eriksson, “Balanced Crys- tal Orbital Overlap Population—A Tool for Analysing Chemical Bonds in Solids,” Journal of Physics: Con- densed Matter, Vol. 15, No. 45, 2003, pp. 7751-7761. doi:10.1088/0953-8984/15/45/014 [42] H. F. Franzen, “Structure and Bonding in Metal-Rich Com- pounds: Pnictides, Chalcides and Halides,” Progress in Solid State Chemistry, Vol. 12, No. 1, 1978, pp. 1-39. doi:10.1016/0079-6786(78)90002-X [43] G. Melnyk, A. Leithe-Jasper, P. Rogl and R. Skolozdra, “The Antimony-Iron-Niobium (Sb-Fe-Nb) System,” Jour- nal of Phase Equilibria, Vol. 20, No. 2, 1999, pp. 113-118. Copyright © 2011 SciRes. MSA
|