Classification with binary gene expressions

doi:10.4236/jbise.2009.26056

Paper Menu >>

Journal Menu >>

Vol.2, No.6, 390-399 (2009)

doi:10.4236/jbise.2009.26056

JBiSE

Classification with binary gene expressions

Salih Tuna, Mahesan Niranjan1

1School of Electronics and Computer Science, University of Southampton, Southampton, UK.

Email: mn@ecs.soton.ac.uk

Received 30 March 2008; revised 25 May 2009; accepted 3 June 2009.

ABSTRACT

Microarray gene expression measurements are

reported, used and archived usually to high

numerical precision. However, properties of

mRNA molecules, such as their low stability and

availability in small copy numbers, and the fact

that measurements correspond to a population

of cells, rather than a single cell, makes high

precision meaningless. Recent work shows that

reducing measurement precision leads to very

little loss of information, right down to binary

levels. In this paper we show how properties of

binary spaces can be useful in making infer-

ences from microarray data. In particular, we

use the Tanimoto similarity metric for binary

vectors, which has been used effectively in the

Chemoinformatics literature for retrieving che-

mical compounds with certain functional prop-

erties. This measure, when incorporated in a

kernel framework, helps recover any informa-

tion lost by quantization. By implementing a

spectral clustering framework, we further show

that a second reason for high performance from

the Tanimoto metric can be traced back to a

hitherto unnoticed systematic variability in ar-

ray data: Probe level uncertainties are system-

atically lower for arrays with large numbers of

expressed genes. While we offer no molecular

level explanation for this systematic variability,

that it could be exploited in a suitable similarity

metric is a useful observation in itself. We fur-

ther show preliminary results that working with

binary data considerably reduces variability in

the results across choice of algorithms in the

pre-processing stage s of microarray analysis.

Keywords: Microarray Gene Expression; Binary

Gene Expressions; High N umerica l Prec ision ; mRN A

Molecules

1. INTRODUCTION

It is anecdotally known and has been formally estab-

lished recently that gene expression measurements ar-

chived in microarray repositories are reported to a far

higher numerical precision than is supported by the un-

derlying biology of the measurement environment. Here,

precision refers to the difference between representing

the mRNA abundance, or relative abundance, of a gene

to several decimal places (e.g. 2.4601) and retaining

only the binary information as to whether the gene is

expressed or not. Shmulevich and Zhang [1] recommend

that gene expressions should be quantized to binary pre-

cision and Hamming distance between signatures used

as distance metric in solving class prediction problems.

Their starting point in defining binary expressions is a

“notion of similarity used by biologists when comparing

gene expressions from different samples... counting the

number of genes that show significant differential ex-

pression”. From this premise, th ey give an algorithm for

binarizing gene expressions and show that a multi di-

mensional scaling (MDS) projection of the data sepa-

rates different types of tumors. More recently, Zilliox

and Irizarry [2] introduce the concept of gene expression

“barcodes”, which are essentially binary representations

of transcriptomes, and present impressive results on pre-

dicting tissue types. These authors take a very different

approach in that they scan through a very large number

of archived datasets of a particular array type to con-

struct barcodes. Genes that are frequently expressed

across the whole ensemble are set to be ON and the oth-

ers set OFF. In our own recent work [3], we show ed that

progressive quantization of gene expression measure-

ments, right down to binary levels, loses very little in-

formation as far as the quality of inference is con cerned.

We were able to demonstrate this on a range of different

inference problems including classification, cluster

analysis, determination of genes that are periodically

expressed and the analysis of developmental time course

data.

Why would we be interested in low precision, or bi-

nary, representations? The initial motivation comes from

the underlying biology. mRNA is only available in very

S. T una et al. / J. Biomedical Science and Engineering 2 (2009) 390- 399

391

small quantities in cells and are extracted fro m a popula-

tion of cells rather than from a single cell. Further, the

process of microarray hybridization itself is a stochastic

one, the effect of which is pronounced when small

numbers of molecules are involved. All these reasons put

together make one sceptical about high precision repre-

sentations of the transcriptome, i.e. the signal available

may only be reliable to low precision. Critical appraisals

of microarray technology, while recognising good re-

producibility of technical replicates, often identifies

large variations with respect to biological replicates. One

such survey by Draghici et al. [4] concludes:

“...the existence and direction of gene expression

changes can be reliably detected for the majority of

genes. However, accurate measurements of abso-

lute expression levels and the reliable detection of

low abundance genes are currently beyond the

reach of microarray technology.”

Artificially inflated precision can potentially hurt. A

plethora of sophisticated inference methods (e.g. Bayes-

ian inference) have been applied to microarray data. Al-

gorithmic complexity of such models is generally de-

rived from how well noise is captured. High precision

gives the illusion of complex noise structures leading to

the use of such algorithms. If the data were far simpler,

one would impose a far higher sense of parsimony in

model selection. Simple classification rules offering

good performance (e.g. the top scoring pairs of genes

approach of Geman et al. [5]) on some problems also

bears testimony to this point. Motivated by the above,

we ask the following research question: If transcriptome

can be represented at low precision, binary for instance,

can we take advantage of properties of high dimensional

binary spaces to achieve increased classification per-

formance? We show that this is indeed the case, by use

of a particular similarity metric between high dimen-

sional binary vectors, the so called Tanimoto metric.

Following experiences seen in the chemoinformatics

literature, we embed this similarity metric in a kernel

discriminant framework (support vector machines-SVM)

and show that very high classification accuracies are

obtainable with binary representation of expression pro-

files. We offer explanations for why such increased per-

formances can be achieved, and attribute this to two

reasons: a) the training of class boundaries that happen

in SVMs, and b) a hitherto unnoticed probe level uncer-

tainty in microarray data.

Finally, the analysis of microarray data goes through a

number of stages of processing steps: background inten-

sity correction, within array normalization, between ar-

ray normalization and algorithms for detecting differen-

tially expressed genes. A user has a choice of several

algorithms at each of these steps and a very large choice

if we consider combinations of available algorithms. A

particular appeal of working with binarized representa-

tions, as shown by preliminary results in this paper, is

that the algorithmic variability in inference is drastically

reduced without compromising the quality o f inference.

2. RESULTS

2.1. Classification

Table 1 compares classification performances of several

classifiers on six microarray class prediction datasets. In

all cases the accuracies are averaged over 25 random

partitions of the data into training and test sets, and

standard deviations in performance across these parti-

tions is also given. In all the different problems we

checked to ensure that our implementation of the linear

SVM classifier acting on raw data performed as well as

the results quoted in the original publication or some

other publication that used the dataset, thus confirming

the correctness of our implementation. Note that in all

the tasks considered, comparing data represented at raw

and binary precisions and classifying with linear SVMs,

we note that binarising the data has not lost much dis-

crimination. In fact in some of the tasks binarization has

actually improved performance. Secondly, in half the

tasks considered, the use of Tanimoto kernel SVM im-

proves the results of binarized classification. Where

there is not an improvement, the method is at least as

good as a linear SVM on binarized data.

Our simulations also show that in all the tasks consid-

ered the distance to template methods perform signifi-

cantly worse than the corresponding kernel methods.

This is true both for templates set as centroids and for

centroids positioned optimally by genetic search. In two

of the four datasets considered, optimization of tem-

plates quickly led to overtraining, resulting in classifiers

whose performance on test data (entries in Table 1) were

worse than their initial values (which were the perform-

ances with templates at centroids). In the genetic opti-

mization, we also found that the local search by mutation

was the dominant contributor, showing that the solution

to the optimized distance based classifier was in the vi-

cinity of the centroids. Cross-over operations nearly al-

ways produced far worse solutions and were quickly

abandoned. To explore this further, in addition to the

centroids, we included noisy templates into the search

algorithm, but found no improvement.

2.2. Clustering

Figure 1 shows the eigenvector obtained in spectral

clustering for the widely studied ALL/AML problem

[11], computed in three different ways: raw and bi-

narized data with negative exponential of Euclidean dis-

tance as similarity, and binarized data with Tanimoto

similarity. The scatter clearly shows cluster separation

along the components of the eigenvector. This is also

S. T una et al. / J. Biomedical Science and Engineering 2 (2009) 390- 399

392

reflected in the Fisher scores between clusters and the

corresponding classification errors which are shown in

Ta b l e 2, (columns 4 and 5), where except in one of the

datasets, there is improvement in the cluster tightness

when Tanimoto similarity is app lied. Similarly, in all but

one of the tasks, the resulting classification error rates

are also lower for the Tanimoto metric.

The final column in Table 2 shows classification error

rates arising from spectral clustering when the microar-

ray profile consists of a filtered subset of genes. In each

task we ranked the genes according to their Fisher scores

of discriminating power taken one at a time, precisely

the same way as done by Golub et al. [11], and report

best performing subsets. The difference between the

different distance metrics with subsets of genes is shown

in Figure 2 for four of the tasks. We see that the use of

Tanimoto similarity leads to better separated clusters in

general. Further the better separated clusters also lead to

better discrimination. We emphasize that the clustering

here is done without the use of class labels, and it is to

verify how good the clusters are that we use this infor-

mation. Thus as expected note the accuracies much

lower than when the problem is formulated as a classifi-

cation problem in the first place.

Table 1. Comparison of classification with different types of kernels for SVM.

Dataset Data type Method Accuracy

Raw-Binary Linear- S VM 0.83 ± 0.10

Binary Linear- SVM 0.86 ± 0.08

Binary Tanimoto-SVM 0.87 ± 0.08

Binary Distance-to-class mean 0.79 ± 0.08

West et al. [6]

Binary Distance-to-optimized template 0.77 ± 0.11

Raw-Binary Linear- S VM 0.63 ± 0.12

Binary Linear- SVM 0.67 ± 0.08

Binary Tanimoto-SVM 0.67 ± 0.10

Binary Distance-to-class mean 0.60 ± 0.11

Huang et al. [7]

Binary Distance-to-optimized template 0.66 ± 0.11

Raw-Binary Linear- S VM 0.99 ± 0.01

Binary Linear- SVM 0.96 ± 0.03

Binary Tanimoto-SVM 0.99 ± 0.01

Binary Distance-to-class mean 0.88 ± 0.07

Gordon et al. [8]

Binary Distance-to-optim ize d t emplate 0 .90 ± 0.07

Raw-Binary Linear- S VM 0.99 ± 0.01

Binary Linear- SVM 0.98 ± 0.01

Binary Tanimoto-SVM 0.98 ± 0.01

Binary Distance-to-class mean 0.67 ± 0.02

Brown et al. [9]

Binary Distance-to-optim ize d t emplate 0 .75 ± 0.03

Raw-Binary Linear- SVM 0.78 ± 0.11

Binary Linear- SVM 0.82 ± 0.07

Binary Tanimoto-SVM 0.84 ± 0.03

Binary Distance-to-class mean 0.80 ± 0.07

Alon et al. [10]

Binary Distance-to-optim ize d t emplate 0 .72 ± 0.10

Raw-Binary Linear- S VM 0.96 ± 0.05

Binary Linear- SVM 0.95 ± 0.03

Binary Tanimoto-SVM 0.96 ± 0.04

Binary Distance-to-class mean 0.94 ± 0.02

Golub et al [11].

Binary Distance-to-optim ize d t emplate 0 .92 ± 0.09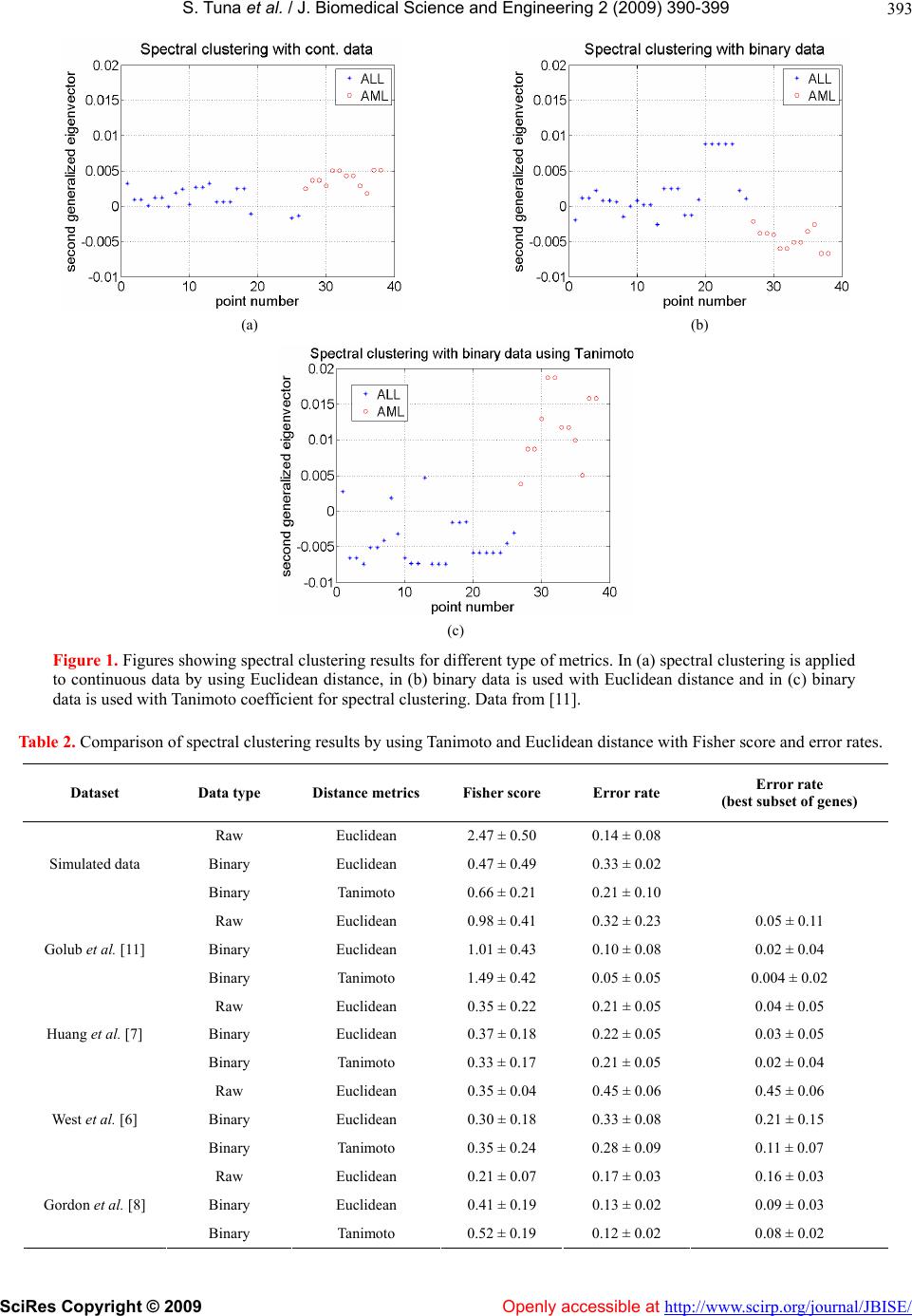

S. T una et al. / J. Biomedical Science and Engineering 2 (2009) 390- 399

393

(a) (b)

(c)

Figure 1. Figures showing spectral clustering results for different type of metr ics. In (a) spe ctral clustering is applied

to continuous data by using Euclidean distance, in (b) binary data is used with Euclidean distance and in (c) binary

data is used with Tanimoto coefficient for spectral clustering. Data from [11].

Table 2. Comparison of spectral clustering results by using Tanimoto and Euclidean distance with Fisher score and error rates.

Dataset Data type Distance metrics Fisher score Error rate Error rate

(best subset of genes)

Raw Euclidean 2.47 ± 0.50 0.14 ± 0.08

Binary Euclidean 0.47 ± 0.49 0.33 ± 0.02

Simulated data

Binary Tanimoto 0.66 ± 0.21 0.21 ± 0.10

Raw Euclidean 0.98 ± 0.41 0.32 ± 0.23 0.05 ± 0.11

Binary Euclidean 1.01 ± 0.43 0.10 ± 0.08 0.02 ± 0.04 Golub et al. [11]

Binary Tanimoto 1.49 ± 0.42 0.05 ± 0.05 0.004 ± 0.02

Raw Euclidean 0.35 ± 0.22 0.21 ± 0.05 0.04 ± 0.05

Binary Euclidean 0.37 ± 0.18 0.22 ± 0.05 0.03 ± 0.05 Huang et al. [7]

Binary Tanimoto 0.33 ± 0.17 0.21 ± 0.05 0.02 ± 0.04

Raw Euclidean 0.35 ± 0.04 0.45 ± 0.06 0.45 ± 0.06

Binary Euclidean 0.30 ± 0.18 0.33 ± 0.08 0.21 ± 0.15

West et al. [6]

Binary Tanimoto 0.35 ± 0.24 0.28 ± 0.09 0.11 ± 0.07

Raw Euclidean 0.21 ± 0.07 0.17 ± 0.03 0.16 ± 0.03

Binary Euclidean 0.41 ± 0.19 0.13 ± 0.02 0.09 ± 0.03 Gordon et al. [8]

Binary Tanimoto 0.52 ± 0.19 0.12 ± 0.02 0.08 ± 0.02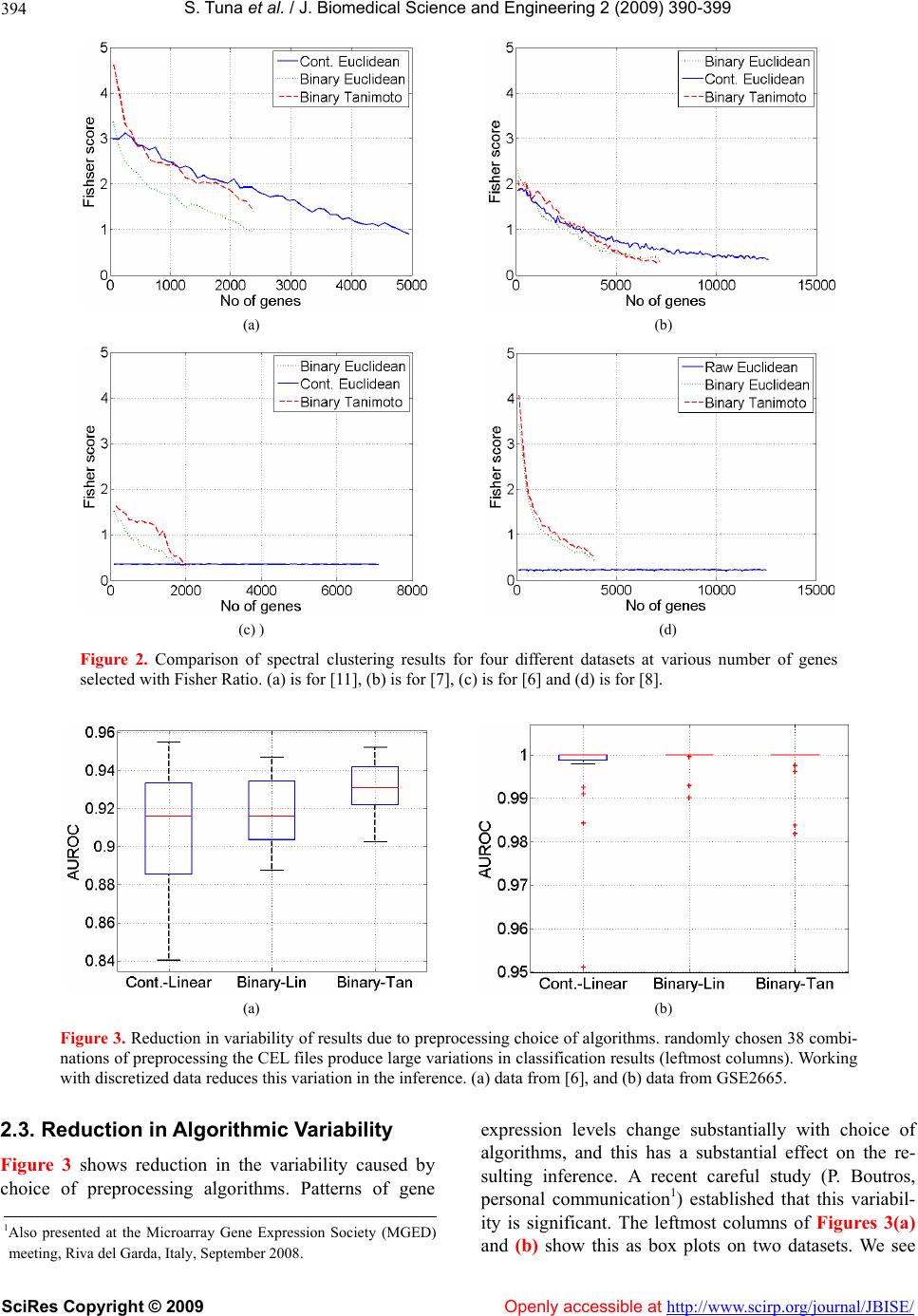

S. T una et al. / J. Biomedical Science and Engineering 2 (2009) 390- 399

394

(a) (b)

Figure 2. Comparison of spectral clustering results for four different datasets at various number of genes

selected with Fisher Ratio. (a) is for [11], (b) is for [7], (c) is for [6] and (d) is for [8].

(a) (b)

Figure 3. Reduction in variability of results due to preprocessing choice of algorithms. randomly chosen 38 combi-

nations of preprocessing the CEL files produce large variations in classification results (leftmost columns). Working

with discretized data reduces this variation in the inference. (a) data from [6], and (b) data from GSE2665.

2.3. Reduction in Algorithmic Variability

Figure 3 shows reduction in the variability caused by

choice of preprocessing algorithms. Patterns of gene

expression levels change substantially with choice of

algorithms, and this has a substantial effect on the re-

sulting inference. A recent careful study (P. Boutros,

personal communication1) established that this variabil-

ity is significant. The leftmost columns of Figures 3(a)

and (b) show this as box plots on two datasets. We see

1Also presented at the Microarray Gene Expression Society (MGED)

meeting, Riva del Garda, Italy, September 2008.

S. T una et al. / J. Biomedical Science and Engineering 2 (2009) 390- 399

395

standard deviations in classifier performances, with out-

liers removed, of 0.032 and 0.134 re spectively, and th ese

reduce to 0.017 and 0.009 when th e ex pr essio n leve ls ar e

binarized. The use of Tanimoto metric (box plots of the

last columns of Figure 3) improves this even further.

3. DATA AND METHODS

3.1. Approach

Our approach was to show that on a sample of classifi-

cation problems published in literature, classification

accuracies reported by the authors do not significantly

degrade when the gene expression data is quantized to

binary precision (i.e. if the gene is expressed or not).

Having achieved this, we implemented a similarity

measure suitable for high dimensional binary spaces in a

kernel framework to show that any loss of performance

is easily recovered. In a number of cases the approach

we took indeed produced better accuracies than working

with the data at raw precision (see Results).

3.2. Tanimoto Similarity

Tanimoto coefficient (

) [12], between two binary vec-

tors, is defined as follow:

cba

T



where

a: the number of expressed points for gene x,

b: the number of expressed points in gene y and

c: the number of common expressed points in two

genes.

Tanimoto similarity ranges from 0 (no points in com-

mon) to 1 (exact match) [13] and is the rate of the num-

ber of common bits on to the total number of bits on two

vectors. It focuses on the number of common bits that

are on. The denominator of Tanimoto coefficient can be

considered as a normalization factor which helps to re-

duce the bias of the vector size (i.e with larger vectors

Tanimoto coefficients work better [14,15]. For this rea-

son Tanimoto coefficient is the preferred similarity

measure in chemoinformatics as all the vectors are long

and there are only few bits on.

Tanimoto kernel can be defined as [16]:

zxK TTT

Tan 

),(

where , and . It follows

from the work of Trotter [16] that this similarity metric

satisfies Mercer conditions to be useful as a valid kernel:

i.e. kernel computations in the space of the given binary

vectors map onto inner products in a higher dimensional

space so that SVM type optimizations for large margin

class boundaries is possible.

xxa T

zzbT

zxcT



Alternate ways of classification of binarized data can

be considered. Motivated by the distance to barcode

classifier built by Zilliox and Irizarry [2] we imple-

mented similar classifiers. An obvious choice in these

circumstances is to set two templates, one to represent

each class, and position them at the centroids of the two

class profiles. This is a distance to mean classifier in

standard statistical pattern recognition terminology. A

particular limitation of this strategy is discussed later.

The barcodes designed by Zilliox and Irizarry [2], how-

ever, are not positioned at the centroids because they are

evaluated by analysing a large number of archived ex-

periments. We also built such discriminant templates, by

doing a stochastic search starting from the centroids as

initial condition. Such an optimization achieves tem-

plates that are better positioned in the input space than

centroids for distance-base d di scri mination.

Clustering is the most popular tool in the analysis of

microarray data. In order to conform whether the use of

Tanimoto distance metric is useful in clustering, we ap-

plied the method of spectral clustering to the classifica-

tion problems considered above. Without knowledge of

the class labels, we clustered each of the datasets into

two clusters using spectral clustering. Subsequently, us-

ing knowledge of the class labels we looked to see how

well separated the clusters formed were, and how accu-

rately the data was allocated to the right clusters. To

measure cluster compactness we used the Fisher ratio as

performance metric:

Fisher Score = 21

21 )(







abs

Checking if the examples were consistently associated

with the right clusters, we computed percentage classifi-

cation errors. The choice of classification problems to

evaluate cluster compactness offers a far better setting

than clustering genes into functions. This is because

cluster analysis, when the data has large numbers of

clusters in them, is notoriou sly unstable. With data taken

from classification problems, we could expect well de-

fined cluster formations (e.g. cancer versus non-cancer),

in which we can compare the role of different distance

metrics.

3.3. Datasets

We give a short description of the datasets used in our

study.

 Yeast dataset compiled and first used in Brown et

al. [9] for predicting yeast gene functions. cDNA

arrays, in which the task is to classify 121 ribo-

somal genes from the remaining 2346 using 79

features. The features are hybridization conditions

during cell cycle progression under different syn-

chronization methods.

 Widely used Leukemia dataset (Golub et al.,

[11]); there are 5000 genes with 38 samples (27

S. T una et al. / J. Biomedical Science and Engineering 2 (2009) 390- 399

396

ALL, 11 AML), being the test subset of the full

dataset.

 Colon da taset (Alon et al., [10]), 2000 genes with

62 samples (20 normal and 42 tumour samples).

 Two Breast cancer datasets, first one from (West

et al., [6]) 7129 genes and 49 samples, (25 ER+

and 24 ER-) and the other Huang et al. [7] 12625

genes with 89 samples (depending on LN status).

 Lung cancer dataset, (Gordon et al., [8]), 12533

genes and 181 samples (31 malignant pleural

mesothelioma (MPM) and 150 adenocarcinoma

(ADCA)).

 53 randomly selected datasets from ArrayExpress

(http://www.ebi.ac .uk/ar rayexpress/) and Gene

Expression Omnibus (GEO)

(http://www.ncbi.nlm.nih.gov/geo/) for probe level

uncertainty analysis analysis. Accession numbers

of these datasets are:

GEO: GSE5666, GSE7041, GSE8000, GSE8505,

GSE6487, GSE6850, GSE8238, GSE2665

Array Express: E-GEOD-6783, E-GEOD-6784},

E-MEXP-1403, E-ATMX-30,

E-GEOD-6647, E-GEOD-6620 ,

E-ATMX-13, E-MEXP-1443,

E-GEOD-2450, E-GEOD-2535 ,

E-MEXP-914, E-MEXP-268,

E-GEOD-2848, E-GEOD-2847 ,

E-MEXP-430, E-GEOD-6321,

E-MEXP-70, E-GEOD-1588,

E-MEXP-727, E-TABM-291,

E-GEOD-3076, E-GEOD-1938 ,

E-GEOD-7763, E-GEOD-3854 ,

E-GEOD-1639, E-TABM-169,

E-MAXD-6, E-MEX P-526,

E-GEOD-2343, E-GEOD-3846 ,

E-MEXP-26, E-GEOD-1723,

E-GEOD-1934, E-MAXD-6,

E-MEXP-879, E-GEOD-10262,

E-GEOD-10422, E-MEXP-998,

E-MEXP-580, E-GEOD-10072,

E-GEOD-10627.

Web Pages:

http://yeast.swmed.edu/cg i-b in/dlo ad. cgi,

http://data.genome.duke.edu/west.php,

http://data.genome.duke.edu/lancet.php,

http://chestsurg.org/publications/2002-microarray.aspx

 Synthetic data was produced following Dettling

[17], using R code made available by the au-

thors. Data is produced to follow the statistics

(mean and correlation structure) of the leukae-

mia data [11]. We generated several realizations

of 200 samples in 250 dimensions. We explored

varying these values over a range, and results

reported in this paper correspond to the above

figures.

3.4. Spectral Clustering

Spectral clustering uses eigenvectors of the pairwise

similarity matrix to partition the data. The most widely

used distance metric to calculate the similarity matrix is

the negative exponential of a scaled Euclidean distance.













 2

),( exp



where the scale parameter



is a free tuning parameter.

The steps involved in spectral clustering, in which we

replace the similarity measure by Tanimoto similarity

between binary strings, are summarized as follows:

 Pairwise similarity matrix ji

A, between the

genes i and j is calculated by us ing Tanimoto coef-

ficient.

 Following Brewer [18] an exponential is applied:

)1(

exp 

ij



 Compute the normalized Laplacian matrix.

2/12/1  





DL F

 Compute the eigenvalue decomposition of L.

iii DyyLD







)(

 Select the eigenvector corresponding to the second

smallest eigenvalue.

Parameters



and



were tuned by searching over a

range of feasible values: –5.05.0.

Uncertainties in results for cluster analysis were

evaluated by a bootstrap method. For each of the tasks,

100 datasets of the same size as the original data were

created by sampling with replacement before the appli-

cation of the spectral clustering algorithm. Perfor-

mances reported are averages and standard deviations

across these 100 bootstrap samples.

3.5. Optimised Templates

The search to find templates better than class means for

a distance-to-template classifier was implemented as a

stochastic local search by means of a genetic algorithm.

Templates were initialized to class means. At every step

in an iterative search, we randomly changed 20% of the

elements in the two templates, to derive mutated bar-

codes in their vicinity. Throughout the search, we re-

tained ten best template pairs at any iteration. Large

search steps were implemented by crossover operation

between pairs of templates whereby half the bits in the

patterns were swapped between pairs, a standard opera-

tion in genetic algorithms. We evaluated the accuracy of

the resulting classifier and there was an improvement we

retained the mutated templates, and discarded them if

was no improvement.

S. T una et al. / J. Biomedical Science and Engineering 2 (2009) 390- 399

397

that classification by computing distances to a template

is optimal only in the case that the distributions of each

class is Gaussian, isotropic (i.e. variances of each feature

is the same) and these variance s are the same for both [22 ].

3.6. Algorithmic V ariability

We used the EXPRESSO set of algorithms in package

Affy in Bioconductor. For both datasets West et al. [6]

and GSE2665, we worked from the CEL files and app-

lied a total of 38 different preprocessing combinations

from a total of 315 possibilities, randomly chosen.

When any of these assumptions is violated, a distance to

template classifier is no longer optimal. Even under the

mild relaxations of the assumption, that of Gaussian den-

sities with identical but nonisotropic covariance matric-

3.7. Other Details es, the optimal classifier requires computation of second

order statistics in the form of the Mahalanobis distance

to class means. In gene expression data isotropic v ari a tio n

cannot be assumed. Under regulation by combinatorial

transcription factor activity where each transcription fac-

To analyse probe level uncertainties (Milo et al. [19]) we

used the PUMA package (Propagating Uncertainty in

Microarray Analysis), downloaded from the site

(www.bioinf.manch ester.ac.uk/resources/pu ma/).

For quantization of microarray data, we used the method

developed by Zhou et al. [20], which models gene ex- tor may control several genes, correlated expression of

groups of genes should be expected. Indeed, the wide

use of cluster analysis of microarray data is based on the

assumption that correlated expression profiles might su-

pressions as mixture Gaussian densities. For quantiza-

tion to binary levels, two Gaussians are used, resulting in

two means and standard deviations:1





and 2



. ggest co-regulation. Therefore, as uncorrelated features

cannot be assumed, optimal classification is unlikely to

be achieved by distance to template decision rules.

From these a threshold



, is computed as





5.0



)( 2121





 . SVM implementations were done Does the same difficulty arise in the barcode method

proposed by Zilliox and Irizarry (2007)? To verify this

we took three datasets, one of which was not included in

their analysis. Prediction accuracies for these three, co m-

in the MATLAB SVM package described in Gunn [21]

(http://www.isis.ecs.soton.ac.uk/isystems/kernel/).

4. CONCLUSIONS paring the barcode method to Tanimoto-SVM, are shown

in Table 3. We note that training and testing on the same

database, as we have done with Tanimoto-SVM, achiev-

The results suggest that a binary representation for tran-

scriptomic data is indeed suitable and good classification

accuracies can be obtained in this space using suitable es consistently better prediction accuracies than the bar-

code method. But in fairness to the barcode method we

remark that their intention is to make predictions on a

new dataset based on accumulated historic knowledge,

rather than repeat the training/testing process all over

again. On this point, while there is impressive perform-

similarity metrics cast in a kernel framework. There are

two reasons for the superior performance of Tanimoto-

SVM based approach over the distance to template appr-

oach inspired by the barcode approach.

4.1. Distance to Template Classifier

ance reported on the datasets Zilliox and Irizarry (2007).

worked on, the method can fail badly too, as in the case

of the lung cancer prediction task E-GEOD-10072

shown in Table 3.

Why did the distance to template method not perform

well consistently in classification problems? We suggest

this result is largely to be expected. With continuous data,

it is a well known result of statistical pattern recognition

Table 3. Comparison of Tanimoto-SVM with [2]’s barcode.

Dataset Data type Method Accuracy

E-GEOD-10072 Binary Barcode 0.50

Lung Binary Tanimoto-SVM 0.89 ± 0.03

Lung tumor vs. normal Binary Tanimoto-SVM 0.99 ± 0.03

GSE2665 Binary Barcode 0.95

Lymph node/tonsil Binary Tanimoto-SVM 0.99 ± 0.02

lymph node vs. tonsil Binary Tanimoto-SVM 1.0 ± 0.0

GSE2603 Binary Barcode 0.90

Breast Tumor Binary Tanimoto-SVM 0.99 ± 0.01

Breast Tumor vs. normal Binary Tanimoto-SVM 0.99 ± 0.01

Openly accessible at

S. T una et al. / J. Biomedical Science and Engineering 2 (2009) 390- 399

398

(a) (b)

Figure 4. A systematic variation in probe level uncertainty of Affymetrix microarray data. (a) On 53 randomly

chosen arrays we plot the average uncertainty of determining expression levels against the number of genes de-

tected as present. Only liner regression lines are shown for clarity. (b) Scatter plots of uncertainties against number

of expressed genes, and the linear regression lines, for the three datasets analysed in this paper.

4.2. Probe Level Uncertainty

The Tanimoto similarity metric attaches higher scores to

profiles with large numbers of expressed genes. For

example if we consider two pairs of vectors with

[1 0 0 0 0 0 0 0] [1 1 0 0 0 0 0 0],

[1 1 0 0 0 0 0 0] [1 1 1 0 0 0 0 0]

In both cases Hamming distance, thus Euclidean dis-

tance, is one. The Tanimoto similarities between these

pairs, however, are different: 0.5 for the first pair and

0.66 for the seco nd. We suggest that a reason why such a

weighting on the similarity scores translates to improve

clustering and class prediction performance comes from

the uncertainties associated with microarray measure-

ments. We found a systematic variation in uncertainties

in expression levels as function of the numbers of ex-

pressed genes in an array. To illustrate this we used a

probabilistic model of encapsulating probe level uncer-

tainties introduced in Milo et al. (2003) [19], and plotted

the average uncertainty in expressed genes as a function

of the number of genes marked as expressed under our

quantization scheme for several arbitrarily chosen data-

sets.

Figure 4 shows the variation in uncertainty with

numbers of expressed genes, for three of the datasets on

which we report classification results, and for 50 arbi-

trarily taken datasets from archives. We see that there is

a systematic reduction in probe level uncertainty as the

number of expressed genes in an array gets larger2. We

offer no molecular level explanation for this, but the

effect is systematic and its impact on the Tanimoto-SVM

is clear. Arrays with larger numbers of expressed genes

are being measured with higher levels of confidence.

Hence if we were to increase the weighting given to

similarities between such profiles we would expect in-

creased performance. Such probe level uncertainty has

been of interest to other researchers, too. Rattray et al.

[23] and Sanguinetti et al. [24] show how cluster analy-

sis and visualization in a subspace by principal compo-

nent projections can be carried out incorporating probe

level uncertainty. In general these are errors-in-variables

type models. We believe accounting for probe level (and

other low level) uncertainties in microarray analysis is

an important topic, and the systematic variability we

have noted here may well be an aspect that other re-

searchers can exploit in microarray inference.

REFERENCES

[1] I. Shmulevich and W. Zhang, (2002) Binary analysis and

optimization-based normalization of gene expression

data, Bioinformatics, 18(4), 555–565.

[2] M. J. Zilliox and R. A. Irizarry, (2007) A gene expre-

ssion bar code for microarray data, Nature Methods,

4(11), 911–913.

[3] S. Tuna and M. Niranjan, (2009) Inference from low

precision transcriptome data representation, Journal of

Signal Processing Systems, [Online, 22 April 2009], doi:

10.1007/s11265-009-0363-2.

[4] S. Draghici, P. Khatri, A. C. Eklund, and Z. Szallasi,

(2006) Reliability and reproducibility issues in DNA mi-

croarray measurements, Trends in Genetics, 22(2), 101–

109.

[5] D. Geman, C. d’Avignon, D. Q. Naiman, and R. L.

Winslow, (2004) Classifying gene expression profiles

from pairwise mRNA comparisons, Statistical Applica-

tions in Genetics and Molecular Biology, 3.

[6] M. West, C. Blanchette, H. Dressman, E. Huang, S.

Ishida, R. Spang, H. Zuza n, J. A. Olson, J. R. Marks, a nd

2We stress that this variation is not a consequence of amplifying noise

in the data of normalised poor quality arrays; i.e. for an array

scanned at low intensity, normalization amplifies noise; the effect o

such noise would be to increase the average uncertainty when more

and more genes are taken as expressed. This is precisely the opposite

of what we see in Figure 4.

S. T una et al. / J. Biomedical Science and Engineering 2 (2009) 390- 399

399

J. R. Nevins, (2001) Predicting the clinical status of hu-

man breast cancer by using gene expression profiles

Proceedings of National Academy of Sciences, 98(20),

11462–11467.

[7] E. Huang, S. H. Cheng, H. Dressman, J. Pittman, M.

Tsou, C. Horng, A. Bild, E. S. Iversen, M. Liao, C. Chen,

M. West, J. R. Nevins, and A. T. Huang, (2003) Gene ex-

pression predictors of breast cancer outcomes Lancet,

361, 1590–1596.

[8] G. J. Gordon, R. V. Jensen, L. Hsiao, S. R. Gullans, J. E.

Blumenstock, S. Ramaswamy, W. G. Richards, D. J.

Sugarbaker, and R. Bueno, (2002) Translation of micro-

array data into clinically relevant cancer diagnostic tests

using gene expression ratios in lung cancer and meso-

thelioma, Cancer Research, 62(17), 4963–4967.

[9] M. P. S. Brown, W. N. Grundy, D. Lin, N. Cristianini, C.

W. Sugnet, T. S. Furey, M. Ares, and D. Haussler, (2000)

Knowledge-based analysis of microarray gene expression

data by using support vector machines, Proceedings of

National Academy of Sciences, 97(1), 262–267.

[10] U. Alon, N. Barkai, D. A. Notterman, K. Gish, S. Ybarra,

D. Mack, and A. J. Levine, (1999) Broad patterns of gene

expression revealed by clustering analysis of tumor and

normal colon tissues probed by oligonucleotide arrays,

Proceedings of National Academy of Sciences, 96(12),

6745–6750.

[11] T. R. Golub, D. K. Slonim, P. Tamayo, C. Huard, M.

Gaasenbeek, J. P. Mesirov, H. Coller, M. L. Loh, J. R.

Downing, M. A. Caligiuri, C. D. Bloomfield, and E. S.

Lander, (1999) Molecular classification of cancer: Class

discovery and class prediction by gene expression moni-

toring, Science, 286(5439), 531–537.

[12] T. T. Tanimoto, (1958) “An elementary mathematical

theory of classification and prediction,” IBM Internal

Report.

[13] P. Willett, (2006) Similarity-based virtual screening using

2d fingerprints, Drug Discovery Today, 11(23/24), 1046–

1053.

[14] P. Willett, J. M. Barnard, and G. M. Downs, (1998)

Chemical similarity searching, Journal of Chemical In-

formation and Computer Sciences, 38(6), 983–996.

[15] J. D. Holliday, N. Salim, M. Whittle, and P. Willett,

(2003) Analysis and display of the size dependence of

chemical similarity coefficients, Journal of Chemical In-

formation and Computer Sciences, 43(3), 819–828.

[16] M. Trotter, (2006) Support vector machines for drug

discovery. PhD thesis, University College London, UK.

[17] M. Dettling, (2004) BagBoosting for tumor classification

with gene expression data, Bioinformatics, 20(18), 3583–

3593.

[18] M. Brewer, (2007) Development of a spectral clustering

method for the analysis of molecular data sets, Journal of

Chemical Information and Modeling, 47(5), 1727–1733.

[19] M. Milo, A. Fazeli, M. Niranjan, and N. D. Lawrence,

(2003) A probabilistic model for the extraction of expres-

sion levels from oligonucleotide arrays, Biochemical So-

ciety Transactions, 31(6), 1510–1512.

[20] X. Zhou, X. Wang, and E. R. Dougherty, (2003) Binari-

zation of microarray data on the basis of a mixture model,

Molecular Cancer the Rapeutics, 2(7), 679–684.

[21] S. Gunn, (1998) Support vector machines for classifica-

tion and regression, Tech. Rep., University of South-

ampton.

[22] R. O. Duda, P. E. Hart, and D. G. Stork, (2001) Pattern

Classification, John Wiley & Sons, USA, ISBN 0-41-

05669-3.

[23] M. Rattray, X. Liu, G. Sanguinetti, M. Milo, and N.

Lawrence, (2006) Propagating uncertainty in microarray

data analysis, Briefings in Bioinformatics, 7(1), 37–47.

[24] G. Sanguinetti, M. Milo, M. Rattray, and N. D. Lawrence,

(2005) Accounting for probe-level noise in principal

component analysis of microarray data, Bioinformatics,

21(19), 3748–3754.