 Open Journal of Discrete Mathematics, 2011, 1, 139-152 doi:10.4236/ojdm.2011.13018 Published Online October 2011 (http://www.SciRP.org/journal/ojdm) Copyright © 2011 SciRes. OJDM Optimal Trajectory of Underwater Manipulator Using Adjoint Variable Method for Reducing Drag Kazunori Shinohara JAXA’S Engineering Digital Innovation Center, Japan Aerospace Exploration Agency, Sagamihara City, Japan E-mail: shinohara@06.alumni.u-tokyo.ac.jp Received June 28, 2011; revised July 30, 2011; accepted August 16, 2011 Abstract In order to decrease the fluid drag on an underwater robot manipulator, an optimal trajectory method based on the variational method is presented. By introducing the adjoint variables, which are Lagrange multipliers, we formulate a Lagrange function under certain constraints related to the target angle, target angular velocity, and dynamic equation of the robot manipulator. The state equation (the partial differentiation of the La- grange function with respect to the state variables), adjoint equation (the partial differentiation of the La- grange function with respect to the adjoint variables), and sensitivity equation (the partial differentiation of the Lagrange function with respect to torques) can be derived from the stationary conditions of the Lagrange function. Using the state equation, we can calculate the state variables (angles, angular velocities, and angu- lar acceleration) at every time step in the forward time direction. These state variables are stored as data at every time step. Next, by using the adjoint equation, we can calculate the adjoint variables by using these state variables at every time step in the backward time direction. These adjoint variables are stored as data at every time step. Third, the sensitivity equation is calculated by using both the state variables and the adjoint variables. Finally, the optimal trajectory of the manipulator is obtained using the sensitivities. The proposed method is applied to the problem of two-link manipulators. It can obtain the optimal drag reduction trajectory of the manipulator under the constraints mentioned above. Keywords: Robot Manipulator Dynamics, Optimal Trajectory, Adjoint Variable Method, Euler-Lagrange Equation, Fluid Drag Force, Calculus of Variations 1. Introduction Presently, we are facing serious environmental problems such as global warming and abnormal climatic condi- tions, which are closely related to the ocean. Therefore, the establishment of ocean study technology is extremely important. Since the 1990s, researchers have investigated the development of underwater robot manipulators for oceanic studies [1-6]. In an extreme environment such as the abyssal ocean, it is difficult to supply energy to manipulators. However, because of fluid tractions, the energy consumption of an underwater manipulator is greater than that of a manipu- lator in air. In order to reduce the energy consumption, it is important to determine the optimal trajectory to reduce the drag on the manipulator. Optimal time control for a manipulator trajectory was studied in the 1970s [7,8]. Kahn and Roth first presented an optimal time control method based on kinematic dy- namics [9]. Vukobratovic and Kiranski presented an op- timal time control method based on dynamic program- ming [10]. Townsend et al. presented optimal control by approximating a function [11]. Lee et al. presented the formulation of a genetic algorithm based on trajectory planning [12]. Constantinescu et al. presented a method for determining smooth and time-constrained optimal path trajectories for a robot manipulator [13]. These studies were carried out with the objective of constructing an optimal time trajectory for a manipulator, from its initial position to the target position. On the other hand, Eiji presented a method for determining the minimum energy trajectory of an underwater manipulator [14]. Uno et al. presented a minimum torque change model [15] A method for drag reduction control has not been de- veloped thus far. A marine robot has energy limitations during its operations. Therefore, drag reduction control  K. SHINOHARA 140 under an extreme environment is crucial for low energy consumption. In this study, we propose an optimal trajectory method for reducing the drag on the manipulator. As the ma- nipulator moves from its initial position to the target po- sition, the fluid generates an external force on the ma- nipulator. A method based on the variational principle is developed to determine the optimal trajectory to reduce the drag. This method is called the adjoint variable me- thod. The adjoint variable method is based on a varia- tional method. By introducing Lagrange multipliers called adjoint variables, we transform the constrained optimization of the cost function into the unconstrained optimization of the Lagrange function. The cost function is defined as the fluid drag on the manipulator. The La- grange function is formulated under the constraints of the robot manipulator dynamics. The stationary conditions (the state equation, adjoint equation, and sensitivity equation) are derived from the Lagrange function. An algorithm is developed on the basis of the stationary conditions. First, the state variables (the angle, angular velocity, and angular accelerations) are calculated by using the state equation in the forward time direction and stored as data at every time step. Next, by using the state variables at every time step, we calculate the adjoint variables by using the adjoint equation in the backward time direction. Finally, the sensitivity (gradient) is cal- culated at every time step, and the time history of the joint torques is determined. Using this optimal trajectory algorithm developed in three phases (state analysis, adjoint analysis, and sensi- tivity analysis), we resolve the problem of the two-link manipulator. The effectiveness of the algorithm is then verified by comparing it with the optimal time control methods described in the literature. 2. Theory 2.1. Variable In this paper, the two-dimensional motion of a manipu- lator with respect to the x-y plane is considered, as shown in the Figure 1. The links are arranged in the shape of a circular cylinder. The manipulator consists of two links that are connected by joints. The coordinates at each joint are defined. The joints and links are numbered from the base to the tip. The angles with respect to joint i are defined as 1, 2qi i (1) The angular velocities with respect to joint i are de- fined as: 1, 2qi i (2) 1 q 2 q 0 x 0 y 0 z 1 y1 x 2 y2 x 1 r 1 l 2 r 2 l Joint 2 Joint 1 Link 2 Link 1 Figure 1. Two-link manipulator. The angular accelerations with respect to joint i are defined as 1, 2qi i (3) In this study, the variables obtained from Eq.(1) to Equation (3) are called state variables (q = (1212 12 )). The penalty parameters with respect to the angle and angular velocity are defined as ,,,,qqqq ,qq 1,2,3,4i i (4) Variables with respect to the angular accelerations () are defined as 12 ,qq 1, 2i i (5) The variables obtained from Equation (5) are called adjoint variables (λ=(λ1, λ2)). The torques with respect to joint i are defined as 1, 2i i (6) The masses with respect to link i are defined as 1, 2mi i (7) The diameters with respect to link i are defined as 1, 2di i (8) The lengths with respect to link i are defined as 1, 2li i (9) The lengths from the centroid of a link to joint i are defined as 1, 2ri i (10) The drag coefficients with respect to link i are defined as 1, 2Ci i (11) The density of the water is defined as (12) Copyright © 2011 SciRes. OJDM  K. SHINOHARA 141 The translational veloci de (13) The sign function sgn(x) is def ties with respect to link i are fined as 1, 2vi i ined as 0 sgn0 if0 1if 0 xx x 1 ifx (14) In order to derive the dynamics of an underwater robot m em order to minimize the cost function under certain con- anipulator, the external force exerted by the fluid drag needs to be added to the robot manipulator dynamics. The fluid drag on an object is proportional to the square of the object’s speed [16]. The fluid drag always has a positive value in the calculation of the robot manipulator dynamics. With respect to the motion direction of the manipulator, the fluid drag acts in the opposite direction in a real environment. Therefore, the sign of the fluid drag direction has to be determined according to the mo- tion of the manipulator. The motion direction of the ma- nipulator can be identified by the sign of the translational velocities. .2. Probl2 In straints, a Lagrange function is formulated by introduc- ing the adjoint variables. The input data are the time his- tories of the torques (τ1, τ2) from the start time 0 to the end time t. The optimal trajectory is searched for in the set of inputs. After determining the values of τ1 and τ2, the angle, angular velocities, and angular accelerations are determined using the state equation from start time 0 to the end time t. The tip of the underwater manipulator moves from the initial position to the target position. The objective of this study is to reduce the fluid drag by the 2D trajectory of the manipulator. The cost function is defined as 12 DD N (15) (16) 2 1122 3142 11 11 0 22 22 0 22 3142 d0 d0 t t Nqaqb qcqd qtqa qa qtqbq b qcq d 22 2 32 11111 sgn 6 DCdlqq 1 (17) 22 2 22 2ll q llqq 2 22 22112 11212 2 2 2 2 23 3 3 D Cdllll lq (18) where the parameters a, b, c, and d in Equation (16) are constants. The first and second terms in Equation (16) are the constraints with respect to the target angle a of joint 1 and target angle b of joint 2, respectively. The third and fourth terms in Equation (16) are the con- straints with respect to the target angular velocity c of joint 1 and target angular velocity d of joint 2, respec- tively. Equations (17) and (18) represent the fluid drag on link 1 and link 2, respectively (see Appendix A). In order to simplify the formulation of the adjoint variable method in this study, it is assumed that the inequality 11 lq 21 20lq q is satisfied at all times. The La- grange function is defined as 12 1122 DD NFFLJF (19) where equations F and F co 12 nstitute the state equation. This state equation represents the robot manip quation of the Lagrange function int variable λ is called the state ulator dy- namics. In this study, a weak formulation is applied to the Lagrange function by the time integration of the state equation. The Lagrange function can also be formulated by a strong formulation that satisfies the equation at every time step. 2.3. State Equation The partial differential e ith respect to the adjow equation: 1 111 d00 LL L F dt (20) 2 222 d00 d LL L F t Equations (20)-(21) represent the robot d nipulator as (21) ynamic ma- ,Mqq Cqqfq (22) The parameters M, C, f, and τ represent the i trix, vector of the coriolis and centrifugal fo nertia ma- forces, drag rce, and joint torque, respectively. By using the pa- rameters in Appendix B, Eqaution (22) is written as 5621 131 3 22214 2 A AAq A A AB qA (23) Equation F is defined as Copyright © 2011 SciRes. OJDM  K. SHINOHARA 142 23 25214 213 11 11 36213614 11 22 11 1 2 6 2 11 0 0 22 25 ABAAAB AA Fq A Fq A AAAA AA AA BA AA A A AA (24) where parameters A1 – A14, B1, and B2 are discussed in Appendix B and Appendix C. 2.4. Adjoint Equations uler-Lagrange equations erived from the stationary condition of the Lagrange ons are derived as The adjoint equations are the E d function. The adjoint equati 11 d0 d LL qtq (25) 22 d0 d LL qtq (26) The time derivation of the adjoint variable λ1 is de- rived from Equation (25) (see Appendix D). 111 3141516 210 2725216 217 1 11 2 2710621765216 2 11 22 2 tq aq cBqBA ABAABrABA AA (27) AA A AAAABrA AA The time derivation of the adjoint variable λ2 is de- rived from Equaiton (26). 22242 518 212 25218 21819 1 BAABrABA A 1 2122 181965218 2 1 2 tq bq dBA A A AAA ABrA A The condition of the end time tf is derived from the partial differential equation of the Lagrange function with respect to the state variables as (28) 12 0, 0 ff Lt Lt qq (29) 01, if ti 2 (30) 2.5. Sensitivity Equations rtial differential equation of the Lagrange function with respect to the torque τ is calle on: The pa d the sensitivity equa- ti 12 22 dBA LL 1,( )00 k L Gt 11 1 1 dtA (31) 12 26 2,( ) 22 12 d00 dk AA LL L Gt tA (32) where the subscript (k) represents an iteration, as sh in the Figure 2. The time histories of the torques are iteratively modified from the time histories of the initial torques. The algorithm determines the optimal trajectory by minimizing the Lagrange function. Finally, Gi,(k) own (t) (I = 1, 2) reaches zero if the subscript (k) represents a suffi- cient number of iterations. 2.6. Steepest Descent Method The time histories of the torques are modified by the gradient as Using Equation (29), we obtain the following equa- tions: 1, 11,1,kk k ttG t (33) tt 2, 12,2,kk k G t (34) er to robustly converge to the optimal trajec- tory and to avoid numerical vibration and di this study, the parameter α is set to 0.1. 3. The data of the every time step are stored in the PC econd phase, using the state variable at The value of the coefficient α should be sufficiently small in ord vergence. In Algorithm The algorithm is shown in the Figure 2. In the first phase, the state variable (q) is calculated from the start time to he end time in the forward direction. t state variable at emory. In the sm every time step, we can calculate the adjoint variables (λ) from the end time to the start time in the backward direc- tion. The adjoint variables are also stored at every time step. In the third phase, by using the state variable and adjoint variable, we obtain sensitivity G, which is the gradient of the Lagrange function, at every time step. The time histories of the torques are modified by using the steepest descent method. Finally, the results are visu- alized in the case where the position of the manipulator Copyright © 2011 SciRes. OJDM 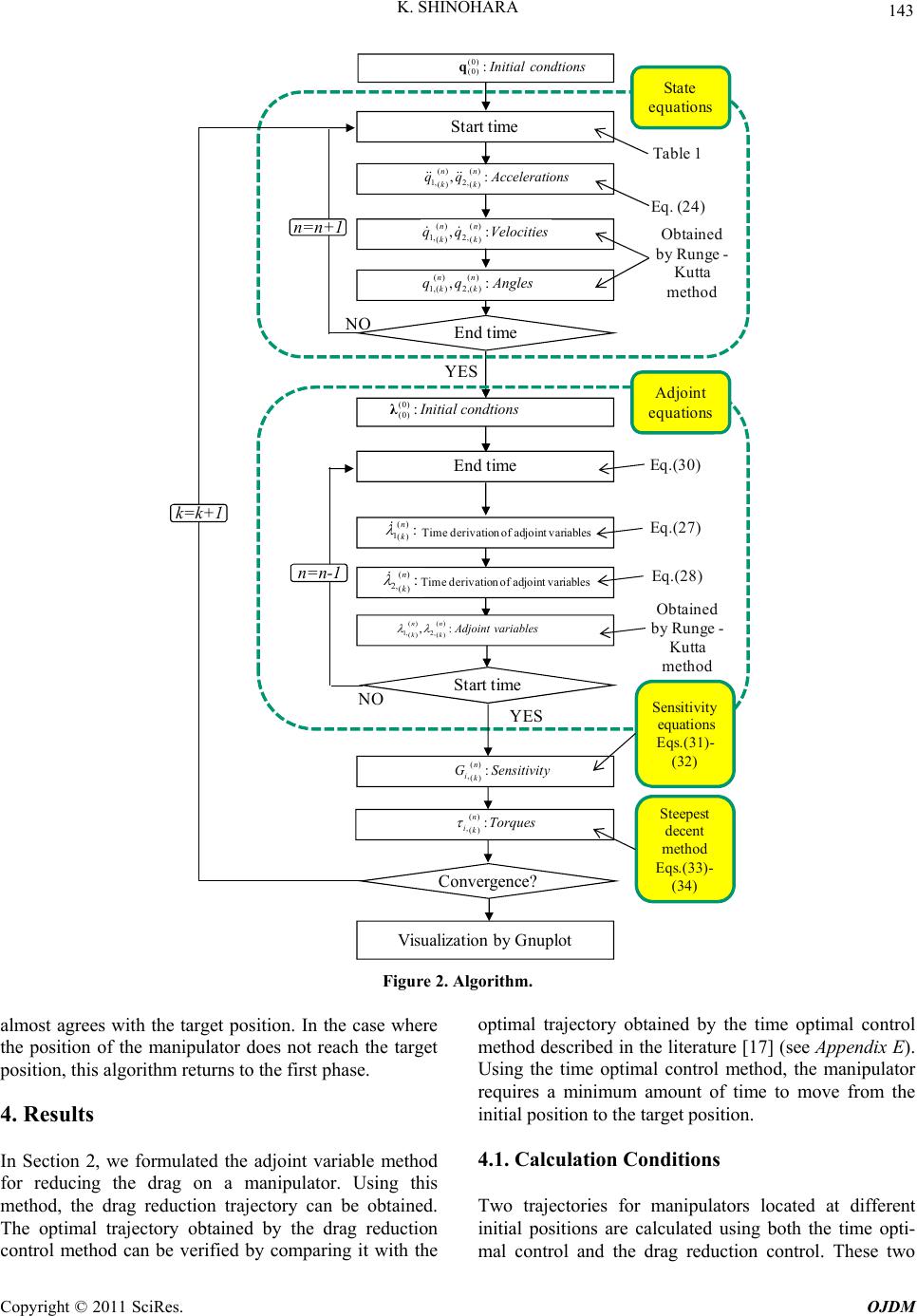 K. SHINOHARA Copyright © 2011 SciRes. OJDM 143 0( 0( qcondtionsInitial: ) ) Convergence? condtionsInitial: )0( )0( λ : )( )( 1 n k : )( )( ,2 n k variablesAdjoint n k n k:,)( )( ,2 )( )( ,1 Start time Visualization by Gnuplot YES NO YES NO n=n+1 n=n-1 Torques n k i: )( )( , Time derivation of adjoint variables Time derivation of adjointvariables Anglesqq n k n k:, )( )(, 2 )( )(, 1 Velocitiesqq n k n k:, )( )( ,2 )( )( ,1 onsAcceleratiqq n k n k:,)( )( ,2 )( )( ,1 Start time End time ySensitivitG n k i: )( )( , Sensitivity equations E qs.(31) - (32) Steepest decent method Eqs.(33)- (34) State equations Adjoint equations Table 1 Eq. (24) Obtained by Runge - Kutta method Eq.(30) End time Eq.(27) Eq.(28) Obtained by Runge - Kutta method k=k+1 Figure 2. Algorithm. almost agrees with the target position. In the case where the position of the manipulator does not reach the target position, this algorithm returns to the first phase. method r reducing the drag on a manipulator. Using this rag reduction trajectory can be obtained. he optimal trajectory obtained by the drag reduction optimal trajectory obtained by the time optimal control method described in the literature [17] (see Appendix E). e time optimal control method, the manipulator requires a minimum amount of time to move from the Using th 4. Results In Section 2, we formulated the adjoint variable fo method, the d T control method can be verified by comparing it with the initial position to the target position. 4.1. Calculation Conditions Two trajectories for manipulators located at different initial positions are calculated using both the time opti- mal control and the drag reduction control. These two  K. SHINOHARA 144 are summarized in able 1. origin (0, 0). The aximum and minimum values for both torque 1 and 37, B2 = 0.3033, and B3 = 0.1482 in the litera- tu gures show angle 1 and angle 2, respec- vely. Angle 1 (q) constantly converges to the target s away from e target angle. After that, by rapidly closing to the tar- itial a calculation conditions are defined as case 1 and case 2. The initial and objective positions T The edge of link 1 is fixed at the m torque 2 are set to ±30 (N) and ±10 (N), respectively. The initial parameters are summarized in Table 1. The solver is applied to the Runge-Kutta method. The time span is set to 0.001. The time histories of the initial torques, τi,(k) (I = 1,2), are constantly defined as zero. The parameters B1 = 4.53 re [17] are used in the manipulator computing model (see Appendix B). The density ρ is set to 1.0. The drag coefficients, C1 in link 1 and C2 in link 2, with respect to the circular cylinder are each set to 0.1. The lengths, L1 of link 1 and L2 of link 2, are each set to 1.0. The diame- ters of the cylinder, d1 and d2, with respect to link 1 and link 2 are each set to 0.01. The penalty parameters, ε1 ~ ε4, are set to 5. 4.2. Computational Results in Case 1 The trajectories for case 1 are shown in the Figure 3 (time optimal control) and the Figure 4 (drag reduction control). The end time is 0.81. The time histories of the angles are shown in the Figure 5. The black and red lines in the fi ti 1 angle. During the first 0.4 s, angle 2 (q2) i th get angle, the time optimal trajectory using the inertia force is created. As shown in the Figure 7, the angular velocities (12 ,qq ) almost become zero at end time tf and satisfy the constraint condition. In link 1 of the manipu- lator, the angular velocity 1 q increases monotonically during approximately the first 0.4 s. After that, the angu- lar velocity 1 q decreases monotonically in order to sat- isfy 10q . In link 2 of the manipulator, the angular velocity 20q from 0 s to 0.4 s. After that, the angular Table 1. Innd target conditions in case 1 and case 2. Parameter Initial condition Target condition 1 q –π/3 0.0 2 q 0.0 0.0 1 q 0.0 0.0 Case 1 0.0 0.0 Case 2 0.0 0.0 2 q 1 q π/3 0.0 2 q –π/6 × 5 0.0 1 q 0.0 0.0 2 q –2 –1.8 –1.6 –1.4 –1.2 –1 –0.8 –0.6 –0.4 –0.2 0 00.511.522.5 Meter (m) Meter(m) Figure 3. Trajectory of two-link manipulator for time op- timal control in case 1. –2 –1.8 –1.6 –1.4 –1.2 Meter( –1 –0.8 –0.6 –0.4 –0.2 0 00.511.522.5 Meter (m) m) Figure 4. Trajectory of two-link manipulator for drag re- duction control in case 1. Figure 5. Time history of angles for time optimal control in case 1. velocity , and it decreases in order to satisfy the constraint, 20q 2 q0 me at end time tf. The time history of the torques for the ti optimal control is shown in the Fig- ure 9. The maximum torque of +30 (Nm) acts on joint 1 during approximately the first 0.4 s. After that, in order Copyright © 2011 SciRes. OJDM  K. SHINOHARA 145 to meet the end constraint condition, the inverse maximum torque of –30 (Nm) The maxi- mum torque of –10 (Nm) acts 0.0 s to 0.15 s. After that, the inverse maximue of +10 (Nm) acts on joint 2 during 0.19 s - . Again, the maximum torque of –10 (Nm) acts on The drag reduction trajectory and te history of angles are shown in Figure 4 and Fi pectively. The end time tf is 1.08 s. The angle s a constant value of zero. By avoiding any extrment of the manipulator, a trajectory from sition to the end position is created for minimum The time history of the angular velshown in the Figure 8. Equaiton (40) is angular ve- locity increases monotonicallyproximately The angular velocity to zero 10q , acts on joint 1. on joint 2 from um torq 0.50 s joint 2. he tim gure 6, res q2 ha a move the initial po drag reduction. ocity is satisfied. The during ap 1 remains close 1 q y. the first 0.4 s. After that, in order to satisfy the constraint condition, 0q , angular velocity q decreases mono- nicall 1 to 2 q by adjusting torque 2 at joint 2. Figure 6. Time history of angles for drag reduction control in case 1. Figure 8. Time history of angular velocities for drag reduc- ion controt l in case 1. Figure 9. Time history of torques for time optimal control in case 1. The time history of the torques for the drag reduction control is shown in Figure 10. The maximum torque of +30 (Nm) acts on joint 1 from 0.0 s to 0.4 s. After that, by loading the inverse torque, torque 1 is adjusted such that 10q 0 . In the case of torque 2, in order to satisfy 2 q and 20q positive torque and the negati , alternative torques using both the ve torque act on joint 2. 4.3. Computational Results in Case 2 For case 2, as shown in Table 1, the trajectory of the manipulator obtained by the time optimal control is shown in the Figure 11. The end time is 0.71 s. The tim nverges to the target angle. During e first 0.2 s, angle 2 (q2) is away from the target angle. After that, by rapidly closing to the target angle, a time optimal trajectory is created using the pullback force e histories of the angles are shown in the Figure 13. The angle q1 constantly co th Figure 7. Time history of angular velocities for time optimal control in case 1. Copyright © 2011 SciRes. OJDM  K. SHINOHARA 146 obtained by the inertia force. The time histories of the angular velocities are shown in the Figure 15. In link 1, the absolute value of the an- gular velocity increases monotonically during ap- proximately th0.35 s. After that, the absolute value of angular velocity decreases monotonically in order to satisfy 1 q e first 1 q 10q the first . . A gular velocity becomes during s. After that, eter The time t trajectory are shown in the Figure 17. The maximum torques of +30 (Nm) act on joint 1 during approximately the first 0.35 s. After that, the inverse torques act on joint 1 so that The cl torque 2 acts on joint 2 during the firs . Again, the clockwise torque takes effect after .45 el the coion, a tra otion of the manipulator, the manipulator is prevented target angle. ink 2 of the manipulator moves in a straight path with n- 0.18 al 2 q param e histories of t 20q turns to o 2 q h20q rques for the time-optim 10q . ockwise t 0.1 s. The counterclockwise torque takes effect from 0.1 s to 0.45 s 0 s. For case 2, as shown in Table 1, the trajectory of the manipulator obtained by the drag reduction control and the time history of angles for drag reduction control in case 2 are shown in the Figure 12 and the Figure 14, respectivy. The end time is 1.08 s. In order to reduce st functsmall angle for q2 is selected at every time step. To prevent the generation of drag by any ex m from swinging link 2 with respect to the L respect to the target position. The time histories of the angular velocities are shown in the Figure 16. Equation (40) is satisfied. The absolute value of the velocities, 1 q , increases monotonically. After that, the absolute value of the velocities, 1 q , de- creases monotonically in order to satisfy 10q . Angu- lar velocity 2 q increases monotonically. After that, 2 q decreases monotonically in order to satisfy 20q . Figure 10. Time history of torques for drag reduction con- trol in case 1. Mer Meter (m) et m 0 0.5 1 1.5 2 2. 1 0.8 0.6 0.4 0.2 0 –0.2 –0.4 –0.6 0.8 Figure 11. Trajectory of two-link manipulator for te op- timal control in case 2. im Meter (m) Meter (m) 0 0.5 1 1.5 2 2.5 0.8 0.6 0.4 0.2 0 –0.2 –0.4 Figure 12. Trajectory of two-link manipulator for drag- reduction control in case 2. Figure 13. Time history of angles for time optimal control in case 2. Copyright © 2011 SciRes. OJDM  147 K. SHINOHARA Figure 14. Time history of angles for drag reduction control in case 2. Figure 15. Time history of angular velocities for time opti- mal control in case 2. Figure 16. Time history of angular velocities for drag re- duction con Figure 17. Time history of torques for time optimal control in case 2. Figure 18. Time history of torques for drag reduction con- trol in case 2. ure 18. The clockwise torque 1 takes effect during ap- proximately the first 0.25 s. After 0.25 s, the counter- clockwise torque takes effect. The clockwise and coun- terclockwise torques act alternately. The clockwise torque acts on joint 2 during the first 0.2 s. The counterclock- wise torque takes effect from 0.2 s to 0.4 s. After ap- proximately 0.43 s, the alternative torque acts on joint 2. 5. Conclusions We proposed the adjoint variable method for obtaining an optimal trajectory in order to decrease the fluid drag on a manipulator when the manipulator moves from its initial position to the target position. By considering hy- drodynamic effects, we formulated the dynamics of an s the fluid drag. By introducing the adjoint The time histories of the torques are shown in the Fig- underwater robot manipulator. The cost function was defined a trol in case 2. Copyright © 2011 SciRes. OJDM  K. SHINOHARA Copyright © 2011 SciRes. OJDM 148 ariable, we formulated the Lagrange function under certain constraints, which consisted of the target angle, target angular velocities, and robot manipulator dynam- ics equations. The gradient of the Lagrange function with respect to the torque was derived from the stationary condition. The algorithm was developed on the basis of the adjoint variable method. This algorithm can be suffi- ciently converged to the optimum value under the c straints, and it can determine an optimal trajectory to reduce the fluid drag under the constraints. Simulation results showed that the performance ca enhanced for the control of an underwater manipulato By using this approach, we can use the motion to reduce fluid drag. It may be important to note that significant performance enhancement is achieved by the motion o es v on- n be r. f the manipulator. . Referenc6 [1] T. L. McLain, S. M. Rock, and M. J. Lee, “Experiments in the Coordinated Control of an Underwater Arm/Vehi- cle System,” Autonomous Robots, Vol. 3, No. 2-3, 1996, pp. 213-232. doi:10.1007/BF00141156 [2] K. N. Leabourne and S. M. Rock, “Model Development of an Underwater Manipulator for Coordinated Arm-Ve- hicle Control,” Proceedings of the OCEANS 98 Confer- ence, Nice France, No. 2, 1998, pp. 941-946. [3] J. Yuh, S. Zhao and P. M. Lee, “Application of Adaptive erver Control to an Underwater Manipu- onal Conference on Robotics and Auto- Disturbance Obs lator,” Internati mation, Vol. 4, 2001, pp. 3244-3249. [4] S. Sagara, T. Tanikawa, M. Tamura and R. Katoh, “Ex- periments on a Floating Underwater Robot with a Two- Link Manipulator,” Artificial Life and Robotics, Vol. 5, No. 4, 2001, pp. 215-219. doi:10.1007/BF02481505 [5] G. R. Vossoughi, A. Meghdari and H. Borhan, “Dynamic Modeling and Robust Control of an Underwater ROV Equipped with a Robotic Manipulator Arm,” 2004 Japan USA Symposium on Flexible Automation, Denver USA, 2004. [6] K. Ioi and K. Itoh, “Modelling and Simulation of an Un- derwater Manipulator,” Advanced Robotics, Vol. 4, No. 4, 1989, pp. 303-317. doi:10.1163/156855390X00152 [7] M. L. Nagurka and V. Yen “Optimal Design of Robotic Manipulator Trajectories: A Nonlinear Programming echnical Report CMU-RI-TR-87-12, the te, Carnegie Mellon University, April, ia, Philadelphia, nd Control, Approach,” T Robotics Institu 1987. [8] M. Žefran, “Review of the Literature on Time-Optimal Control of Robotic Manipulators,” Technical Report MS- CIS-94-30, University of Pennsylvan 1994. [9] M. E. Kahn and B. Roth, “The Near Minimum-Time Control of Open-Loop Articulated Kinematic Chains,” Journal of Dynamic Systems, Measurement a Vol. 93, No. 3, 1971, pp. 164-172. doi:10.1115/1.3426492 [10] M. Vukobratović and M. Kirćanski, “A Method for Op- timal Synthesis of Manipulation Robot Trajectories,” Journal of Dynamic Systems, Measurement, and Control, Vol. 104, No. 2, 1982, pp. 188-193. doi:10.1115/1.3139695 [11] M. A. Townsend, “Optimal Trajectories and Controls for pulator with Acceleration Parameterization,” Jour- and Systems of Coupled Rigid Bodies with Application of Biped Locomotion,” Thesis (Ph.D.), University of Wis- consin Madison, Madison, 1971. [12] Y. D. Lee and B. H. Lee, “Genetic Trajectory Planner for a Mani nal of Universal Computer Science, Vol. 3, No. 9, 1997, pp. 1056-1073. [13] D. Constantinescu and E. A. Croft, “Smooth Time-Optimal Trajectory Planning for Industrial Ma- nipulators Along Specified Paths,” Journal of Robotic Systems, Vol. 17, No. 5, 2000, pp. 233-249. doi:10.1002/(SICI)1097-4563(200005)17:5<233::AID-R OB1>3.0.CO;2-Y [14] E. Shintaku, “Minimum Energy Trajectory for an Un- derwater Manipulator and Its Simple Planning Method by Using a Genetic Algorithm,” Advanced Robotics, Vol. 13, No. 6-13, 1999, pp. 115-138. [15] Y. Uno, M. Kawato and R. Suzuki, “Formation and Con- trol of Optimal Trajectory in Human Multijoint Arm Movement,” Biological cybernetics, Vol. 61, No. 2, 1989, pp. 89-101. doi:10.1007/BF00204593 [16] J. Saleh, “Fluid Flow Handbook,” McGraw Hill, New York, 2002. [17] H. Kobayashi et al., “The Robot Control Actually,” The Society of Instrument and Control Engineers, Tokyo, 1997.  K. SHINOHARA 149 the coordinates (x0,y0,z0) 0 Appendix A: Fluid Drag The underwater manipulator receives a reactive force when it moves to the target position. In this section, the fluid force on the manipulator is derived. In this study, the link is defined as a circular cylinder. The transla- tional velocity with respect to (=(0,0,0)) of link 1 is given by 1 1011 11 1 00 0 00 0 00 x q q vvωx (35) here the variable v0 represents the velocity on the round. In this study, the base is fixed at v0 = 0. The ariable ω1 is the angular velocity vector in link 1. The anslational velocity in link 2 is given by w g v tr 12 11 212 0 0 2 00 00 00 21 22 11 lq vvωx qq lqxqq (36) Using Equation (35), we obtain the fluid drag in link 1 as 12 1101111 1 0 sgnd 2 l Cdxq x vωx 122 111 111 0 0 sgn()d 2 l Cdxqxqx 1 0 (37) The function 11 sgn q always becomes the function 1 sgn q because x1 > 0. Therefore, 11 sgn xq 1 sgn q The integration in Equation (37) is not related to the function 1 sgn q . Thus, Equation (37) becomes 32 32 111 1111111 11 00 1sgn sgn 23 6 00 0 0 CdlqqCdl qq D D (38) The fluid drag in link 2 is (see next page) In this study, in order to simplify the formulation of the adjoint variable method, it is assumed to satisfy the inequality as 112 120lql qq (40) n (39) bec Appen The variables used in this study can be defined as fol- lows: 2 Thus, Equatioomes (see next page) dix B: Definition of Variables 222 11223 cos BB BBq (42) 2 2 2 221121211212 2 0 2 22 2 2 21111122122 0 0 sgn d 2 0 0 2sgn 2 l l Cdlqx qqlqx qqx Cdlqlqq qxq qx 112 122 d lqx qqx 22 2 21 22112122 0 sgn d 2 l Cdlqx qqx 0 vωx (39) 222 2222 2 2221121212 12 2 33 l Cdllllqlllqq2 2 2 sgnd3 ll Cdlqxqqxq 22 122112 122 0 2 0 2 0 0 vωx 22 0 D D (41) Copyright © 2011 SciRes. OJDM  K. SHINOHARA 150 2223 cos BB q (43) 2 2 331 sin Bq q (44) 2 2 4312232 2cos cos Bqqq Bqq (45) 2 2 5312232 2sin sin Bqqq Bqq (46) 261 3 2cos BB q (47) 2732 2sin Bq q (48) 283 sin Bq (49) 293 cos Bq (50) 103 12 sin Bq q (51) 2 113 12 cos Bq q (52) in 123 122 2s Bq qq (53) 22 134 1525126 17 1 282 cos 2 BqBr BlqBqBqqBq (54) 2 145 261 2 7 1 28 2 Br BqB qqBq (55) 15 5 2 sin 22 6 17 1 282 BqB qBqqBq (56) 166 17 2 2 Bq Bq (57) 1741525 12 2cos 6 172 2 BqBr Blq Bq Bq (58) 187 182 2 Bq Bq (59) 195251 c2 os Br Blq (60) where the variables B1 – B8 are defined as follows: 2 21 ml 112 111 22 11 1112 2221 16 12 zz zz zzg BI I Imr dl m (61) 22 2 2 2221 zzg I mrml 22 222 22 dl mrmmrml 16 12 22 22 22 22 22222 16 12 zz zzg dl BI Imrmmr 2 1 (62) 322 Bmrl (63) 3 41111 sgn( ) 6 BCdlq (64) 52 2 BCd 22 l (65) 2 22 6112 3 l Blll (66) 2 721 2 3 Blll 2 (67) 2 2 83 l B (68) Appendix C: Robot Manipulator Dynamics The translational acceleration, a1, of the barycenter in link 1 is as 1111 11 2 11 11 111 000 00000 00 rr rq qqq aωrωωr 11 0 rq (69) The translational acceleration a2 of the barycenter in link 2 is given by 2 21122222 2 22 11 12 2 12 12 sin cos 000 0010 00 000 0 qq lq qq r qq qq 22 11 2 cossin 00qq lqr 0 aReωrωωr 2 2 1121222 12 2 1121122 12 cos sin sin cos 0 lqqlqqr qq lqqlqqr qq (70) The vect with respect to the tip o sents the rotation matri coordinates (x1,y1,z1). The translational forces f1 and f2 with respect to l 2 or ei represents the angular acceleration vector f link i. The matrix 1 R repre- x from coordinates (x2,y2,z2) to 2 ink 1 and link 2 are given by 222 m fa D (71) 1 11 221 m 1 aRfD (72) f 1 where the matrix represents the rotation matrix from the coord (x2,y2,z2). 1 2 R inates (x1,y1,z1) to the coordinates 22 1sin cos 0qq 22 2 cossin 0 00 qq R (73) In this study, the buoyancy and gravity are ignored. By equilibrant moment of the relation between link 1 and link 2, it is derived as Copyright © 2011 SciRes. OJDM  K. SHINOHARA 151 2 (74) where the first and second terms on the right- are 222222 2 InIaωωfr hand side 2 212212 00 00 x zz I 22 2 00 0 0 00 y I qq Iqq I α (75) 2 2222 122 12 0000 00 00 00 0 x y z I I qqI qq ωIω 0 0 (76) where the matrix I2 represents the inertia tensor of lin The vector α2 represents the acceleration of link 2. equilibrant moment at joint 1 is derived as (77) where the matrix I1 represents the inertia tensor of link 1. Th The adjoint equations are derived. The v are k 2. The 11 122112211 1111 1 nRnfr Rfrl Iαω Iω e vector α1 represents the acceleration of link 1. With respect to the z axis, moments n1 of the joint 1 and n2 of the joint 2 are defined as torques τ1 and τ2. Equation (24) is thus derived. Appendix D. Derivation of Adjoint Equations ariables 1 q, 2 q, 1 q , 2 q , 1 q , and 2 q independent of each other. The partial differential equation of the Lagrange function with respect to q is given by 1 113141 0 1 210 2725216 217 1 516 11 1d 22 2 t Ltq aq cBqBA q AA BA ABrA BA A (78) 11 2710621765216 2 2 AA AAA AAAABrA A The partial differential equation of the Lagrange func- tion with respect to q is given by 1 1 1 L q (79) The partial differential equation of the Lagrange func- tion with respect to is given by 2 q 2242 0 2 1d 2 t Ltq bq dBA q 212 25218 21819 1 1 2 122 181965218 2 1 BAABrABA A A AAAA AABrA A (80) The partial differential equation of the Lagrange func- tion with respect to 2 q is given by 2 2 L 518 q (81) Appendix E. Derivation of Adjoint Equations . The parameters are defined as follows: The time optimal control method is described in the lit- erature [17]. The Hamiltonian formulation is applied in time optimal control. Using a Legendre transformation, the Hamiltonian formulation is derived from the Lagran- ian formulationg 11 q (82) 21 q (83) 31 q (8) 42 4 q (85) The state equation is defined as 3 11 4 22 23 2522 12 111 33 44 25 366 2 12 111 d d x xS x xS AA BABA AAA xS t xS AA AAA A AAA (86) The cost function with respect to the time optimal con- trol is given by 00 d1d tt Lt Nt NtN (87) where the constraint N represe and Equation (16). Using the a 3, 4), the Hamiltonian is defined as nts the constraint condition djoint variables pi (i = 1, 2, T L pS (88) where L represents 1 of the integrand in Equation (87). The adjoint equation is given by TT T d d H L t ppS xx (89) The boundary condition of the adjoint equ given by ation is T f f f Nt pt t x x (90) Copyright © 2011 SciRes. OJDM  K. SHINOHARA Copyright © 2011 SciRes. OJDM 152 The Hamiltonian Equation (89) is 13 24 334 1 pxpxpS pS (91) 1 1 d d0p (92) tx Using Equation (89), the adjoint equation is given by 2325 8936 89 24 38 211 3 1 2 AAA AA pp p A 25 2458386112 2A AAAAAAAA 22 11 2898 2898 31 32 22 11 11 d 22 tA A BAAA AAAA pp AA AA 2 dAA BA AA BAAA AA 4 2 1 A 289 8 41 2 1 1 2AAA A p A A 689 42 2 1 2AAA H p A 2 x (93) 27 21027 610 4 AA AA 31 3 113 22 d d BA AA pp p tA p Ax (94) 212 26 AA BA 21 2 22 4 14 d d BA BA 42 3 1 pp p tA p Ax (95) The constraint condition at the end time is given by 111 2 ff ptxt a (96) 222 2 ff ptxt b (97) 0) (98) The gradient is given by 2 B Hpp 2 34 111 34 21 A 333 2( ff ptxtc 444 2(0) ff ptxt d (99) 6 2 1 A HA pp A (100)
|