 Applied Mathematics, 2011, 2, 1270-1278 doi:10.4236/am.2011.210177 Published Online October 2011 (http://www.SciRP.org/journal/am) Copyright © 2011 SciRes. AM Further Results on Pair Sum Labeling of Trees Raja Ponraj1, Jeyaraj Vijaya Xavier Parthipan2 1Department of Mat hem at i cs, Sri Paramakalyani College, Alwarkurichi, Indi a 2Department of Mat hem at i cs, St.John’s College, Palayamcottai, India E-mail: ponrajmath@gma il.com, parthi68@rediffmail.com Received August 4, 2011; revised September 3, 2011; accepted Septe mber 10, 2011 Abstract Let G be a , q graph. An injective map :1,2,, VG p is called a pair sum labeling if the induced edge function, : e fEG Z0 defined by e uvf ufv is one-one and e EG is either of the form 12 2 ,,, q kk k or 12 12 12 ,,, qq kk kk according as q is even or odd. A graph with a pair sum labeling is called a pair sum graph. In this paper we investigate the pair sum label- ing behavior of some trees which are derived from stars and bistars. Finally, we show that all trees of order nine are pair sum graphs. Keywords: Path, Star, Bistar, Tree 1. Introduction Notation 2.1: We denote the vertex and edge sets of star 1,n as follows: The graphs in this paper are finite, undirected and simple. and will denote the vertex set and edge set of a graph G. The cardinality of the vertex set of a graph G is called the order of G and is denoted by p. The cardinality of its edge set is called the size of G and is denoted by q. The concept of pair sum labeling has been introduced in[1].The Pair sum labeling behavior of some standard graphs like complete graph, cycle, path, bistar, and some more standard graphs are investigated in [1-3]. Terms not defined here are used in the sense of Harary [4]. All the trees of order ≤8 are pair sum have been proved in [5]. Here we proved that all trees of order nine are pair sum. Let x be any real number. Then VG EG stands for the largest integer less than or equal to x and stands for the smallest inter greater than or equal to x. 1, ,:1 ni VKuui n and 1, 1 ni EKuui n . 2. Pair Sum Labeling Notation 2.2: We denote the vertex and edge sets of bistar as follows: ,mn B ,,, ,:1,1 mni i VBuvuvim in and ,,, :1,1 mni j EBuvuuvvimj n . Theorem 2.3 [5]: All graphs of order ≤8 are pair sum. Now we derive some pair sum trees which are used for the final section. 3. Pair Sum Labeling of Star Related Graphs Definition 2.1: Let G be a ,pq 2,, graph. An injective map :1, VG p is called a pair sum labeling if the induced edge function, : e fEG Z 0 defined by is one-one and e EG q is either of the form or 12 /2 ,,, q kk k ,,..., q kk kk Here we prove that some trees which are obtained from stars are pair sum. Theorem 3.1: The trees with vertex set and edge set given below are pair sum. ,(1 5) i Gi 12 (1)/2(1)/2 according as q is even or odd. A graph with a pair sum labeling defined on it is called a pair sum graph. 1) 11, :1 6 ni VG VKvi and  R. PONRAJ ET AL. 1271 . . . 3 , 3 . 7 11,112 2334 4556 ,,,,, n EGEKuvvvvv vvvv vv Then is a pair sum graph. 1 G 2) 21, :1 7 ni VG VKvi and 21,667 1223 34455 ,,,,,, n EGEKuv vvvv vvvvvvvu Then is a pair sum graph. 2 G 3) 31, :1 7 ni VG VKvi and 31,556 6712 2334 4 ,,,,,, n EGEKuvvvvv vv vv vv vu Then is a pair sum graph. 3 G 4) 41, :1 4 nii VG VKvwi and 41,112334122 344 ,,,,, ,. n EGEKuww wuwwwv vvv vv vu Then is a pair sum graph. 4 G 5) 51, ,:1 3 nii VG VKvwi and 51,12311223 ,,, ,, n EGEKuvuvuvv wvwvw Then is a pair sum graph. 5 Proof 1): Define G 1 :1,2,,fVGn by 123 456 1,7,5, 1, 3, 5,7 24,1 2 i fu fvfvfv fv fv fv fuii n and (1)/2 26,1 2 ni fuii n . Then is a pair sum tree. □ 1 Proof 2): Define a map G 2 :1,2,,fVGn 8 by and (/2) 28,1 22 nii fuiin . Then is a pair sum graph. □ 2 Proof 3): Define a map G 3 :1,2,,fVGn8 by 123 4567 1 (/2) 3,6, 1, 4, 2, 3,4, 1,7 , 12,10,12 ni fv fvfv fvfvfv fv fu fui in fuiin . Then is a pair sum graph. □ 3 Proof 4): Define a map G 4 :1,2,,fVGn 9 by 12 34 1234 1, 3,2, 1,4, 5,6, 7,4. fufv fvfv fv fwfwfw fw For the other vertices we define, (1)/2 52,1 2 72,1 2. i ni fuiin fuii n Obviously f is a pair sum labeling. □ Proof 5): Define 5 :1,2,,fVGn7 by 123 123 (1) 1, 2,3,4, 3,5, 7, 24,1 2 22,12. i ni fufvfvfv fw fwfw fuii n fuiin Obviously f is a pair sum labeling. □ Illustration 1: A pair sum labeling of the tree with 1 G 10n is 75 3 1 –5 –7 –1 12 84 –4 –12 –8 –6 8 10 –14 8 10 12 14 16 –7 –9 –11 –13 –15 7 9 15 13 11 –12 123 4567 1 1 3,6, 1, 4, 1,3,4, 2, 7, 42,1 2 i fv fvfv fvfv fvfv fu fu fuiin Copyright © 2011 SciRes. AM  1272 R. PONRAJ ET AL. Illustration 2: A pair sum labeling of the tree with is 3 G 9n –6 –3 –1 –4 1 2 3 4 –9 –7 –5 –3 3 5 7 8 9 10 11 12 –11 –12 –13 –14 9 10 11 12 13 –10 –11 –12 –13 Illustration 3: A pair sum labeling of the tree with is 5 G 11n 10 8 6 12 14 16 –4 –6 –8 –10 –12 4 –3 7 –5–2 3 2 –3 –1 2 1 5 7 9 11 13 15 –5 –7 –9 –11 –13 3 –1 4. Bistar Related Graphs In this section we show that some trees which are ob- tained from bistar are pair sum. Theorem 4.1: Let G be the tree with ,:1 6 mn i VG VBwi and ,112234455 ,,,,, mn EGEBvwwwwwvw wwww 6 . 8 Then G is a pair sum graph. Proof: Define :1,2,,fVGmn and 1234 56 4, 5, 6,2, 7,4, 2,1. fw fwfwfw fwfwfu fv Case 1): mn Case 2): mn Assign the label to as in case 1). De- fine ,1 ii uvin 8,1 ni fun iim n 2 and 213, 12 mn i fun iim n Case 3): mn Assign the label to ,1 ii uvim as in case 1). De- fine 11,12 mi fvm iinm 210, 12. mn i fvmiinm Then G is a pair sum graph. □ Theorem 4.2: If G is the tree with ,:13 mn i VG VBwi and ,112233 ,,, mn EGEBuww wwwwvuv . Then G is a pair sum tree. Proof: Define a function :1,2,,fVGmn 5 by 12 3 1, 3,4,1, 2. fufv fwfw fw Case 1): mn . 5,1 i uiin and 3,1 i. viin Case 2): . mn Assign the label to as in case 1). De- fine ,1 ii uvin 5,1 ni funiim n 2 27,12 mn i fun iim n . Then G is a pair sum graph □ 11 3,9, 11, 10, 1. i i fufuii n fvii n Illustration 4: A pair sum labeling of the tree in theo- rem 4.2 with 10m , 6n is given below: Copyright © 2011 SciRes. AM  R. PONRAJ ET AL. Copyright © 2011 SciRes. AM 1273 –4 –3 1 3 2 5 3 4 5 6 7 8 9 7 8 9 10 11 12 –9 –8 –1 –5 –7 –6 15 14 –13 –12 –11 –10 –10 –9 –8 –7 14 13 –14 –13 –12 –11 Theorem 4.3: Let G be the tree with and edge set ,:1 4 mn i VG VBwi ,11223445 ,, ,, , mn EGEBuwwv vww wvwwwuv . Then G is a pair sum tree. and ,1122334 ,,,, mn EGEBuwwwwvvwwwuv Proof: Define . :1,2,,fVGmn 7 Then G is a pair sum graph. by Proof: Define :()1,2, ,6fVG mn 12 34 5 1, 1,4,2, 3,3, 5. fufv fwfw fw fwfw by Case 1): mn 12 34 1, 2,4,1, 3, 4. fufv fwfw fw fw 5,1 i uiin and Case 1): . mn 5,1 i viin 11 6,6, 11 i ufu iin Case 2): mn and Label the vertices and as in case 1) for i ui v 1in 5,1. i vii n . Define 5,1 ni funiim n 2 Case 2): . mn Assign the label to ,1 ii uvin as in case 1). De- fine and 26,1 2 mn i fun iim n . 5,1 ni funiimn 2 Case 3): mn and Assign the label to ,1 ii uvin as in case 1). De- fine 28,1 2 mn i fun iim n . 5,1 mi fvm iinm 2 Case 3): . mn Assign the label to ,1 ii uvin as in case 1). De- fine and 27,1 2 mn i fvmiin m . 8,1 mi fvm iin m 2 and Then G is a pair sum graph. □ Theorem 4.5: Let G be the tree with 2 ()5,1 mn i fvm iinm 2. ,:15 mn i VG VBwi Then G is a pair sum graph. □ Theorem 4.4: The tree G with vertex set and ,:15 mn i VG Bwi ,12233445 ,,,,,. mn EGEBww wuuwwvvw wwuv  R. PONRAJ ET AL. 1274 7 . Then G is a pair sum tree. Proof: Define a function :1,2,,fVGmn by 12 34 5 4, 2,6,1, 1, 3, 4. fufv fwfw fw fwfw Case 1): mn 6,1 i uii n . and 8,1 i vii n . Case 2): mn Assign the label to as in case 1). De- fine ,1 ii uvim 8,1 mi fvmiin m 2 and 212, 12. nm i fvmiin m Then G is a pair sum graph. Illustration 5: A pair sum labeling of the tree in theo- rem 4.5 with , is given below: 6m11n –6 –7 –1 –5 –4 –3 1 3 2 5 3 7 4 9 10 11 12 13 14 15 16 17 –20 –21 11 12 13 14 15 16 17 18 19 –18 –19 –10 –9 –8 –7 –13 12 –11 –17 –16 –15 –14 –13 –12 –11 Theorem 4.6: Let G be the tree with ,:1 4 mn i VG VBwi and ,1 122334 ,, ,, mn EGEBuwwvvwww wwuv . 6 . Then G is a pair sum tree. Proof: Define a function :1,2,,fVGmn by 12 34 1, 1,4,2, 3, 4. fufv fwfw fw fw Case 1): mn 6,1 i uiin and 6,1 i. viin Case 2): .mn Assign the label to ,1 ii uvim as in case 1). De- fine 7,1 mi fvmiin m 2 and 26,1 2 mn i fvm iimn . Case 3): . mn Assign the label to as in case 1). De- fine ,1 ii uvin 5,1 ni funiim n 2 and 28,1 2 mn i fun iim n . Then G is a pair sum graph. □ Theorem 4.7: Let G be the tree with ,:1 4 mn i VG VBwi and ,112233 ,,, mn EGEBvwww wwww 4 . Then G is a pair sum tree. Proof: Define a function :1,2,,fVGmn 6 by 12 34 1, 2,3,1, 2, 3. fu fvfwfw fw fw . Case 1): mn 6,1 i uiim and 13,1 1. i fvii m Case 2): .mn Assign the label to ,1 ii uvim as in case 1). De- fine 2,1 mi fvmiin m 2 and 27,1 2 mn i fumiin m . Case 3): . mn Copyright © 2011 SciRes. AM  R. PONRAJ ET AL. 1275 Assign the label to ,1 ii uvin as in case 1). De- fine 6,1 ni funiim n 2 and 25,1 2 mn i fun iim n . Then G is a pair sum graph. □ Theorem 4.8: The tree G with ,:15 mn i VG VBwi and ,1122344 ,,,, mn EGEBvwww wwvw ww 5 . 7 Then G is a pair sum graph. Proof: Define a map :1,2,,fVGmn by 12 345 1, 2,3,4, 1,5, 4. fu fvfwfw fw fwfw Case 1): .mn 7,1 i uii m and 4,1 i. vii m . Case 2): mn Assign the label to as in case 1). De- fine ,1 ii uvim 4,1 mi fvmiin m 2 and 28,12 mn i fum iin m . . Case 3): mn Assign the label to ,1 ii uvin as in case 1). De- fine 7,1 ni fun iim n 2 and 25,1 2 mn i fun iim n . Then G is a pair sum graph. □ Theorem 4.9: The tree G with ,:15 mn i VG VBwi and ,122 33445 ,,, , mn EGEBww wuvwww ww . Then G is a pair sum graph. Proof: Define a map :1,2,,fVGmn 7 by 12 345 4, 1,6,1, 2, 3, 4. fufv fwfw fw fw fw Case 1): .mn 11 1 5,6,11, 8 i fufuii m fv and 19,1 1 i fuii m . Case 2): .mn Assign the label to ,1 ii uvim as in case 1). De- fine 8,1 mi fvmiin m 2 and 210, 12. mn i fumiin m Case 3): .mn Assign the label to as in case 1). De- fine ,1 ii uvin 5,1 ni funiim n 2 and 213, 12. mn i fun iim n Then G is a pair sum graph. □ Theorem 4.10: The tree G with ,:16 mn i VG VBwi and ,12233455 ,,, ,, mn EGEBwwwuvwww vw ww 6 . Then G is a pair sum graph. Proof: Define a map :1,2,,fVG mn 8 by 12 3456 4, 1,6,1, 2, 3,3, 5. fufv fwfw fwfw fwfw Case 1): .mn 4,1 ,6 ii fuii mfv and Copyright © 2011 SciRes. AM 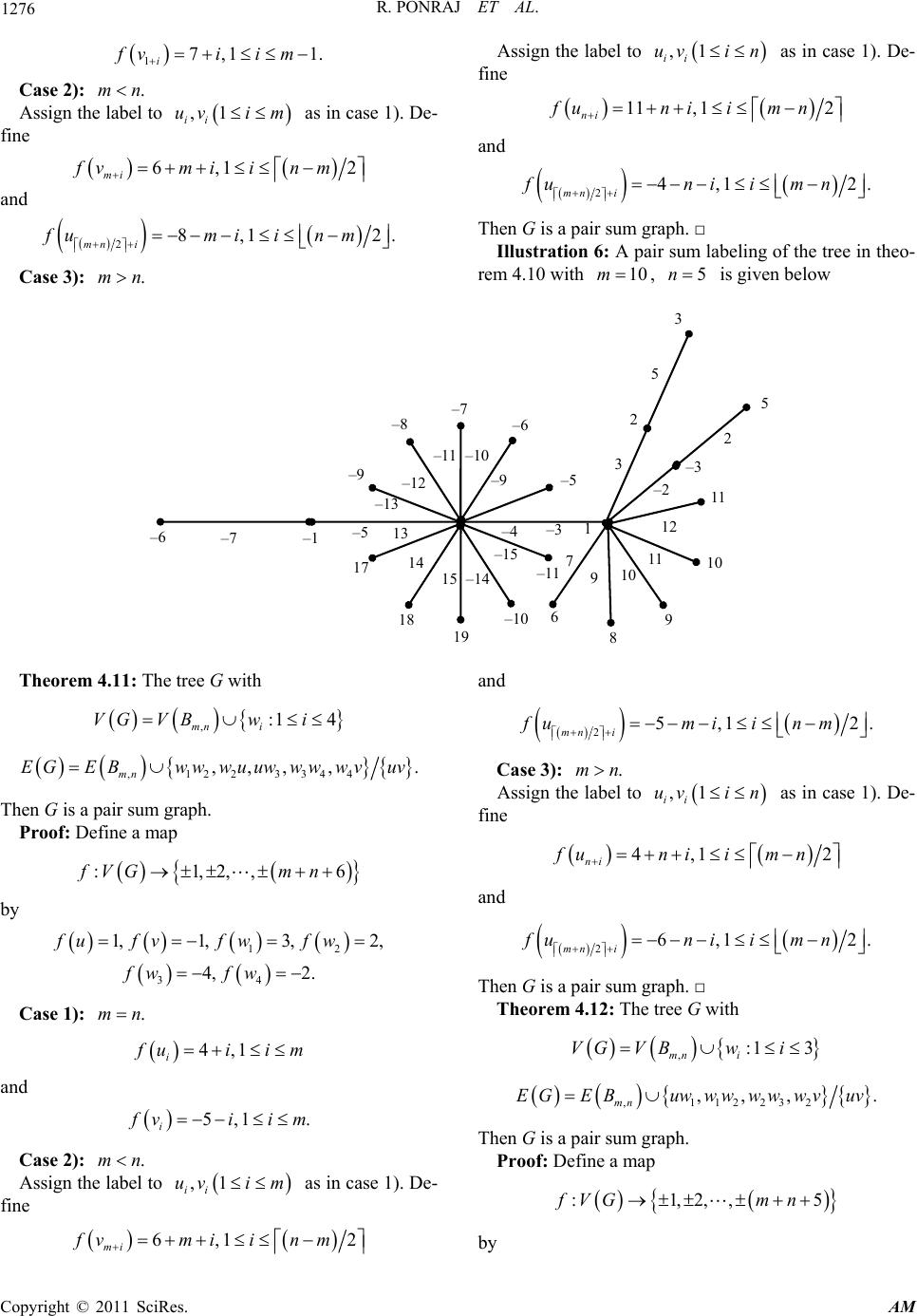 R. PONRAJ ET AL. Copyright © 2011 SciRes. AM 1276 . 17,1 1. i fvii m Case 2): mn Assign the label to as in case 1). De- fine ,1 ii uvim 6,1 mi fvmiin m 2 and 28,12 mn i fum iin m . . Assign the label to as in case 1). De- fine ,1 ii uvin 11, 12 ni funiimn and 24,1 2 mn i funiim n . Then G is a pair sum graph. □ Illustration 6: A pair sum labeling of the tree in theo- rem 4.10 with 10m , 5n is given below Case 3): mn –6 –7 –1 –2 –3 2 5 3 2 5 3 11 10 9 8 10 11 12 –5 13 –4 –3 1 6 7 9 –9 –8 –7 –6 –5 –13 –12 –11 –10 –9 –15 –14 15 14 –11 –10 19 18 17 Theorem 4.11: The tree G with and 25,12 mn i fum iin m ,:1 4 mn i VG VBwi . ,122 3344 ,,, , mn E GEBwwwuuwwwwvuv . 6 Case 3): . mn Assign the label to as in case 1). De- fine ,1 ii uvin Then G is a pair sum graph. Proof: Define a map 4,1 ni funiim n 2 :1,2,,fVGmn and by 26,1 2 mn i funiim n 12 34 1,1,3,2, 4, 2. fu fvfwfw fw fw . Then G is a pair sum graph. □ Theorem 4.12: The tree G with Case 1): .mn ,:13 mn i VG VBwi 4,1 i uii m . and ,112232 ,,, mn EGEBuwwwww wvuv . 5,1 i vii m . Then G is a pair sum graph. Case 2): mnProof: Define a map Assign the label to as in case 1). De- fine ,1 ii uvim :1,2,,fVGmn 5 6,1 mi fvmiin m 2 by  R. PONRAJ ET AL. 1277 12 3 1, 1,2,3, 5. fufv fwfw fw Case 1): .mn 3,1 i uii m and 3,1. i vii m . Case 2): mn Assign the label to as in case 1). De- fine ,1 ii uvim 3,1 mi fvmiinm 2 and 25,12 mn i fum iin m . . Case 3): mn Assign the label to ,1 ii uvin as in case 1). De- fine 3,1 ni fun iim n 2 and 25,1 2 mn i fun iim n . Then G is a pair sum graph. □ Theorem 4.13: The tree G with ,:13 mn i VG VBwi and ,112231 ,,, mn EGEBuwww wwwvuv . 5 Then G is a pair sum graph. Proof: Define a map :1,2,,fVGmn by 12 3 1, 3,2,3, 2. fufvfwfw fw Case 1): .mn 5,1 , i uii m 3,1. i vii m . Case 2): mn Assign the label to as in case 1). De- fine ,1 ii uvim 3,1 mi fvmiin m 2 and 29,12 mn i fumiin m . Case 3): . mn Assign the label to as in case 1). De- fine ,1 ii uvin 5,1 ni funiim n 2 and 27,12 mn i fun iim n . Then G is a pair sum graph. □ Theorem 4.14: The tree G with ,:13 mn i VG VBwi and ,212232 ,,, mn EGEBuwww wwwvuv . Then G is a pair sum graph. Proof: Define a map :1,2,,fVGmn 5 by 12 3 1, 3,5,2, 1. fu fv fwfw fw Case 1): .mn 42,1 i uiim and 2,1 . i viim Case 2): . mn Assign the label to as in case 1). De- fine ,1 ii uvin 32 ,12 ni funiim n and 252 ,12. mn i fun iim n Then G is a pair sum graph. □ Illustration 7: A pair sum labeling of the tree in theo- rem 4.14 with 9m , 6n is given below: Copyright © 2011 SciRes. AM 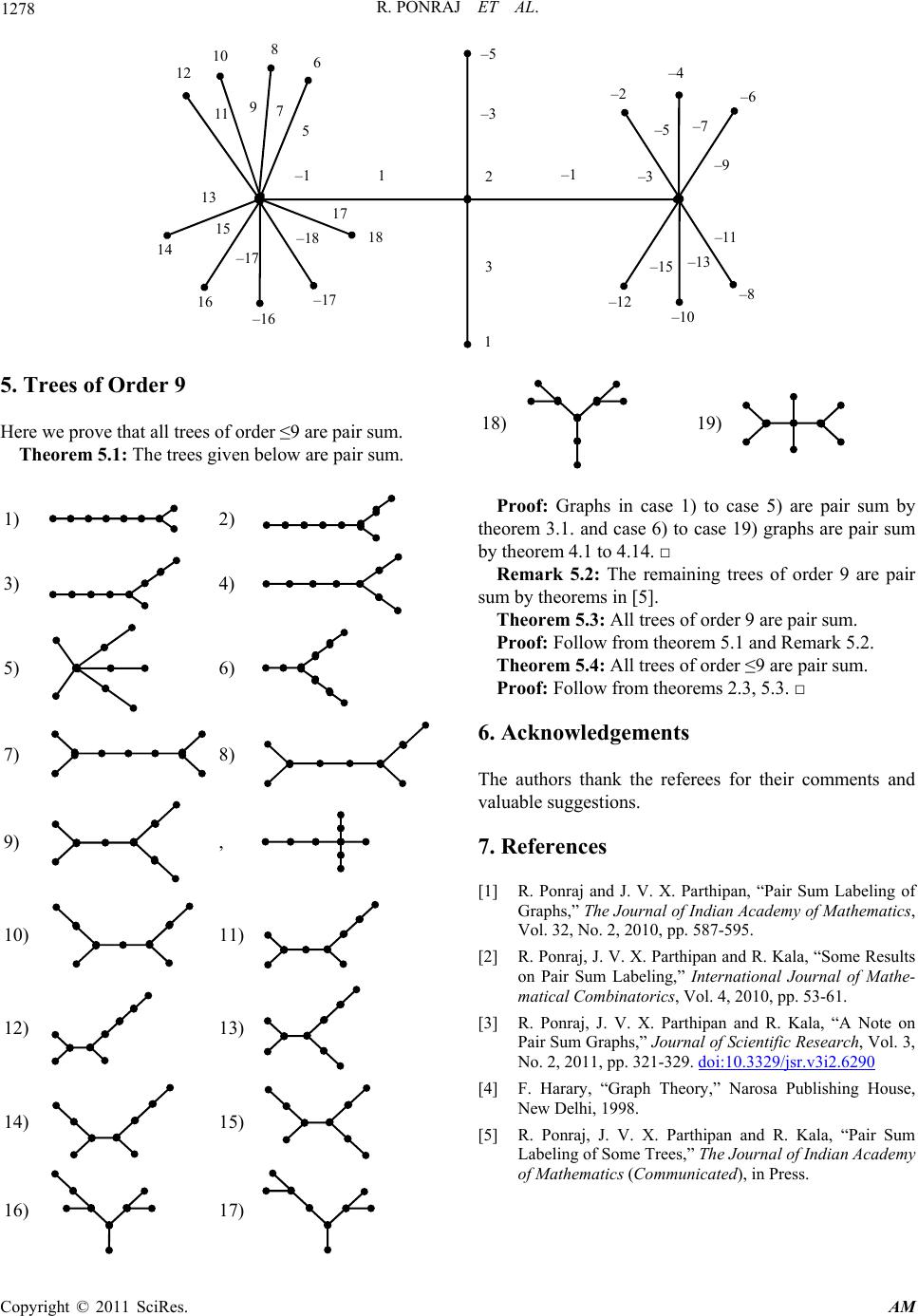 R. PONRAJ ET AL. Copyright © 2011 SciRes. AM 1278 –5 –3 2 3 1 –1 1 –1 –2 –4 –6 –8 –10 –12 –11 –13 –15 –9 –7 –5 –3 12 10 8 6 11 9 7 5 13 15 –17 –18 17 18 –17 –16 16 14 5. Trees of Order 9 Here we prove that all trees of order ≤9 are pair sum. Theorem 5.1: The trees given below are pair sum. 1) 2) 3) 4) 5) 6) 7) 8) 9) , 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) Proof: Graphs in case 1) to case 5) are pair sum by theorem 3.1. and case 6) to case 19) graphs are pair sum by theorem 4.1 to 4.14. □ Remark 5.2: The remaining trees of order 9 are pair sum by theorems in [5]. Theorem 5.3: All trees of order 9 are pair sum. Proof: Follow from theorem 5.1 and Remark 5.2. Theorem 5.4: All trees of order ≤9 are pair sum. Proof: Follow from theorems 2.3, 5.3. □ 6. Acknowledgements The authors thank the referees for their comments and valuable suggestions. 7. References [1] R. Ponraj and J. V. X. Parthipan, “Pair Sum Labeling of Graphs,” The Journal of Indian Academy of Mathematics, Vol. 32, No. 2, 2010, pp. 587-595. [2] R. Ponraj, J. V. X. Parthipan and R. Kala, “Some Results on Pair Sum Labeling,” International Journal of Mathe- matical Combinatorics, Vol. 4, 2010, pp. 53-61. [3] R. Ponraj, J. V. X. Parthipan and R. Kala, “A Note on Pair Sum Graphs,” Journal of Scientific Research, Vol. 3, No. 2, 2011, pp. 321-329. doi:10.3329/jsr.v3i2.6290 [4] F. Harary, “Graph Theory,” Narosa Publishing House, New Delhi, 1998. [5] R. Ponraj, J. V. X. Parthipan and R. Kala, “Pair Sum Labeling of Some Trees,” The Journal of Indian Academy of Mathematics (Communicated), in Press.
|