Journal of Biomaterials and Nanobiotechnology, 2011, 2, 369-377
doi:10.4236/jbnb.2011.24046 Published Online October 2011 (http://www.SciRP.org/journal/jbnb)
369
Flow Rate through a Blood Vessel Deformed Due
to a Uniform Pressure
Amy Cypher1, Mohamed B. Elgindi2, Hatem Kouriachi3, David Peschman4, Reba Shotwell5
1University of Wisconsin-Eau Claire, Eau Claire, USA; 2University of Wisconsin-Eau Claire and Texas A & M University-Qatar,
Doha, Qatar; 3University of Wisconsin-Eau Claire, Eau Claire, USA; 4University of Wisconsin-River Falls, River Falls, USA;
5University of Wisconsin-Madison, Madison, USA.
Received August 29th, 2011; revised September 26th, 2011; accepted October 4th, 2011.
ABSTRACT
In this paper, we present the mathematical equations that govern the deformation of an imbedded blood vessel under exter-
nal uniform pressure taking into consideration the nonliner behavior of th e soft tissue surrounding the vessel. We presen t a
bifurcation analysis and give explicit formulas for the bifurcation points and the corresponding first order approximations
for the non-trivial solutions. We then present the results of a MATLAB program that integrates the equilibrium equations
and calculates the blood flow rate through a deformed cross section for given values of the elasticity parameters and pres-
sure. Finally, we provide (numerical) verification that the flow rate as a function of the elasticity parameters of the soft tis-
sue surrounding the blood vessel is convex, and theref ore validate the invertibility of our model.
Keywords: Blood Vessel, Deformation of Elastic Tube
1. Introduction
Stability analysis for the buckling, post-buckling shapes
and flow rate through an imbedded blood vessel under
uniform external pressure were considered in [1]. In that
paper, the soft tissues surrounding blood vessels are mo-
deled by numerous linear independent springs. However,
biological tissues are well known to respond in a non-
linear fashion to applied forces [2-6]. Since the support
provided by the perivascular tissue is an important con-
tributor to the in vivo structural stiffness of arteries,
which will in turn affect the pressure-flow rate rela-
tionship, there is a critical need for further studies. In this
paper, we examine the effect of replacing the linear
spring in [1] by nonlinear ones on the post-buckling
shapes and on the pressure-flow rate relationship. Fur-
thermore, we verify (numerically) the convexity of the
flow rate as a function of the elasticity parameters. This
convexity of the (direct) problem is important to ensure
its invertibility. That is, to ensure the solvability of the
(more important) inverse problem, namely, to determine
the elasticity parameters of the soft tissue surrounding
the blood vessel from measurements of the deformation,
the pressure, and the flow rate. The paper [1] assumes:
1) The tethering can be represented by numerous in-
dependent springs.
2) The springs are linear.
Motivated by the fact that biological tissues are known
to respond in a nonlinear fashion to applied forces, we
begin our series of studies to improve previous results by
replacing Equation (8) of [1] by a nonlinear function




12
=
F
kBCAC kgBCAC . It is expected that
this nonlinearity will have no effect on the stability
analysis; however, it will alter the post-buckling shapes
and flow rates through them. Interests in these post-
buckling computations will make the present studies
necessary and useful steps in the direction of describing
tethered vessels more precisely. Furthermore, our (nu-
merical) validation of the solvability of the inverse pro-
blem gives the simple physical model used in this project
advantages over more complicated ones. The rest of this
paper is organized in five sections. In Section 1, we de-
fine the variables and formulate the equilibrium equa-
tions. In Section 2, we give a bifurcation analysis of the
equilibrium equations that lead to explicit formulas for
the bifurcation points, dependent on spring stiffness, and
the corresponding first order approximations for the
bifurcation solutions. In Section 3, we show the numeri-
cal formulation [7]. In Section 4, we present our numeri-
cal results. In Section 5, we give some concluding remarks.
2. Mathematical Formulation
We consider the deformation of a thin-walled elastic

Flow Rate through a Blood Vessel Deformed Due to a Uniform Pressure 370
cylinder tethered by continuously distributed nonlinear
springs to a rigid outer cylinder (see Figure 1, below).
The interior cylinder is subjected to internal pressure i,
and external pressure e. This cylinder will remain
circular until a bifurcation pressure difference is exceeded.
P
P
To formulate the mathematical equations governing
the equlibrium, we consider the forces acting on an ele-
mental length of the interior cylinder (see Figure 2,
below).
In Figure 3, below, we analyze changes in the coor-
dinates of an element length due to a displacement from
point A to point B.
2.1. Notations
In the rest of this paper, we use the following notations
for our variables:
i
P
P: Internal pressure
e
S: External pressure : Shearing force
s

: Arc length
t
q
q: Tangential stress
n: Normal stress
M
: Moment
T: Tension

: Local curvature of vessel from x axis
2.2. Assumptions
We make the following assumptions:
1) The flow of blood through a tethered blood vessel is
slow and steady.
2) The cross section does not vary much along a
segment, so that the internal pressure is taken as constant
(locally).
2.3. Remark
From the assumptions above, we conclude that we can
solve for the deformed shape first, then calculate the
flow rate afterward.
2.4. Equilibrium Equations
Balancing forces in the normal direction gives:
=n Tdq dsdS


 (1)
Balancing forces in tangential direction gives:
=0
t
qds SddT

  (2)
Balance of moments gives:
=dM Sds (3)
Assuming the wall thickness to be small compared to
the radius, it follows that the moment M is proportional
to the local curvature, where E and I are material
constants [8]:
d
=d MEI
s

 (4)
Figure 1. Elastic cylinder tethered to a rigid cylinder.
Figure 2. An element length.
Figure 3. A small displacement from A to B.
C
opyright © 2011 SciRes. JBNB

Flow Rate through a Blood Vessel Deformed Due to a Uniform Pressure371
From which

2
2
dd
=
dd
MEI
s
s

 (5)
From (2) we get

2
2
ddd
=0
dd
d
tT
qEI ss
s



 (6)
From (1) we get
dd
=
dd n
S
T
ss




q (7)
And this gives
22
222
d dddd =
dd d dd
n
q TS
TEI
s
ss ssR

 (8)
From (6) we get
2
2
222
ddddd
=0
ddd d
t
EI EIT
q
sss RRs




 ds
(9)
From (8) and (9) we get
3
423 2
423
2
ddd ddd
dd
ddd d
d dd
=0
dd d
n
n
t
q
ss
2
s
ss s
q
qss
s

 











(10)
where
=
s
sR
 (11)
3
=n
n
qR
qEI
 (12)
3
=t
t
qR
qEI
 (13)
We also have
d=cos
d
x
s

(14)
d=sin
d
y
s

(15)
Let 0
F
be the tension per unit length per unit area of
a spring at spring length of 1a

(). >1a
We define
0
=ei PPPF (16)
We assume that the extra force due to deformation is F
and is given by:

12
=

F
kBCAC kgBCAC  (17)
where and are spring constants and g is a
nonlinear function.
1
k2 k
=1
A
Ca (18)

2
=cossin =BCas xas yd
2
(19)
22
22
22
sin1 cos
tan== sec1
cos cos
xx
x
x
xx


 (20)
 


2
22
22
2
sin
sec=tan1 =1
cos
sin cos
=
cos
asy
asx
asy asx
asx
 



 



 

(21)
 


2
2
22
2
2
cos
cos =
sin cos
cos
=
asx
asy asx
asx
d


 

(22)

cos
cos= as
d


x (23)

sin
sin= asy
d


 (24)
But





cos cossin sin
=cos =cos
cos sin
cossin= cos
asx asy
dd
 
 


 



(25)


=coscossinsin
t
FZ
qasxa
d
  

sy



 (26)


=sincoscossin
n
FZ
qasxa
d
  

sy



 (27)

 
12
=

F
ZkZkgZ (28)
=1
Z
da (29)
3. Bifurcation Analysis
For low values of the pressure difference, the interior
cylinder remains circular. As the pressure difference in-
creases byond some critical values, non-circular solu-
tions occur (see Figure 4, below). These critical values
of the pressure difference are called bifurcation points
while the corresponding non-circular solutions are called
bifurcation solutions. It is well known that bifurcation
may occur only at pressure difference values that corre-
spond to a singular linearized problem about the circular
solution.

Flow Rate through a Blood Vessel Deformed Due to a Uniform Pressure 372
Figure 4. Bifurcation points with solutions for N = 2, 3, and 4.
In this section, we present the calculations to find the
bifurcation points: the critical values of the pressure
difference at which the vessel deforms into non-circular
shapes.
First, we set

1
ys

 (local angle)

2Momentys

3Shearys

4Tensionys

5
y
sx

6
y
sy
where 2π
0,sN





is the arclength.
We define the state vector:
   


123456
=,,,,,Ysysysysysysys

(30)
Then the equations of equilibrium can be written as:
 
2
3
42
32
1
1
=,= =
cos
sin
n
t
y
y
yy qP
Ys FYPyy q
y
y












0

(31)
with boundary conditions:

1
π
0=
2
y



36
0= 0=0yy
1
2ππ2π
=2 yNN
 


3
2π=0yN



 
22 22
56 56
2π2π
00=yyyy
NN
 

 
 
,n Pq
=P, and defined by:
t
Pressure difference,
q



151
=sincos cossin
n
FZ
qyasyyas
d

6
y


 

,



151
=coscos sinsin
t
FZ
qyasyyas
d

6
y

  

,
where n and t are the normal and tangential com-
ponents of stress per unit length,
q q

F
Z is the force due
to the springs, which is given by:


12
=

F
ZkZkgZ (32)
where
=1
Z
da (33)
And

22
56
=cos sindasy asy .
(34)
In the circular case, the Basic Solution is given by:







1
2
3
0
4
5
6
π
2
1
0
==
cos
sin
ys s
ys
ys
Ys ys P
ys
s
ys
s

























(35)
where =1da

, , , and =0Z=0
t
q


=0
n
qg.
Assuming that


0g0

, we have




00
=,YPYs F
,
P

, and furthermore


0
Ys satisfies the boundary
conditions for formula (31). The Fréchet derivative of


,
F
YP at the basic solution is given by:

42
15
0
32
15
1
1
010000
001000
0
=
0
sin00000
cos00 000
nn
Ytt
qq
yy
yy
FY qq
yy
yy
y
y
6
6
n
t
q
y
q
y




















 















(36)
where:
=000
0
1156
====
YY
nttt
YYY
qqqq
yyyy


0 (37)
01
5
=cos
nY
qks
y

 (38)
C
opyright © 2011 SciRes. JBNB

Flow Rate through a Blood Vessel Deformed Due to a Uniform Pressure373
01
6
=sin
nY
qks
(39)
y


Therefore, the linearized problem about the
solution is:







(40)
Which may be written as:
basic

0
Ys

0 0
s








1
2
3 11
4
5
6
100 0
00100 0
001cossin
=00100 0
cos00000
sin00 000
Y
ys
ys
ys
Pksks
ys
ys
s
ys
s

















 
56
d
=1 cossinyPykysys
s
  (41)
Integrating twice gives:
2
w
111
d
 

111561
1cossind=yPyky sysscsc
  
 (42)
ith boundary conditions:
 
136
0= 0= 0=0yyy
13
2π
 2π
==0yy
NN

 


55
2π2π2π2π
0=cos sinyy y
NN NN
 

 
 
6
Therefore,
To solve the fferential equation:
1
=
2=0c.
di

11
 
156
1sincos
y
Py
  kysysc s (43)
We write the solution in the form:
1
=1
2n
n
π
== sin
y
sbnNs 



 (44)


5 3
1
=1
cos1 cos
==cos 11
n
n
snN snN
y
xsb
nN nN







(45)
c


6 4
=1
sin1sin1
==sin21 1
n
n
bsnN snN
yy sc
nN nN







(46)
where
Substituting these equations into the differential
equation gives:
=2,3,4,N.
22 1
22
=1
sin1= 0
n
n
k
bnNsnNP



 (47)
22 1
22
1=0,
1
nk
bnNP n
nN

 



>1
n-zero solution (a bifurcation point) to exist,
must be
(48)
For a no
1
b 0

.
ore, Theref
21
2
1=0
1
NP N   (49)
From whice get:
k
h w
*2 1
2
=1 1
Nk
PN N   (50)
here *
N
P is the critica
nt, at which the vessel d
wl pressure value, or bifurcation
poi eforms into a shape with N
axes of symmetry.
This result allows us to find the bifurcation points for
alugiven ves of N and 1 k. Before the first bifurcation
point, for

*
2
0,
P
P

, we have the basic (trivial)
solution which corr
2
esponds to the undeformed shape.
The deformed shapes corresponding to N = 2, 3, 4, ,
N exist for PP

, wherehe circular solution becomes
unstable, ands is lost. A series expansion of
the first order approximations of the bifurcation solutions
are given by formula (43).
Additionally, equating
t
nesunique
N
P with 1N P
 gives us the
pressure where the shape with N axes of symmetry
collapses. For example, the =2N case occurs for 0 ≤
k1 ≤ 24, while the =3N case occurs for 24 ≤ k1 ≤ 120.
4. Numerical Formulati
extern
).
, we write the equili-
on
Due to the assumed uniform al pressure, the vessel
will deform into radially symmetric shapes, with N axes
of symmetry ( N, an integer, 2
Given P, a, N, 1 k, and 2 k
brium equations in the form:
12
=yy

23
=yy

34
=yy


3
32 3
422
2
=ntn yy qqyq
yy
1nN

Then
2
yy y


 

51
=cosyy

61
=sinyy

where
1=y

, 2=y


, 3=y


, 4=y

 , 5=yx, 6=yy
and



56

coscos sinsin
Za
syasy
 =
t
F
q


 (51)

d



56
=sincos cossin
n
FZ
qasya
d


sy


 

(52)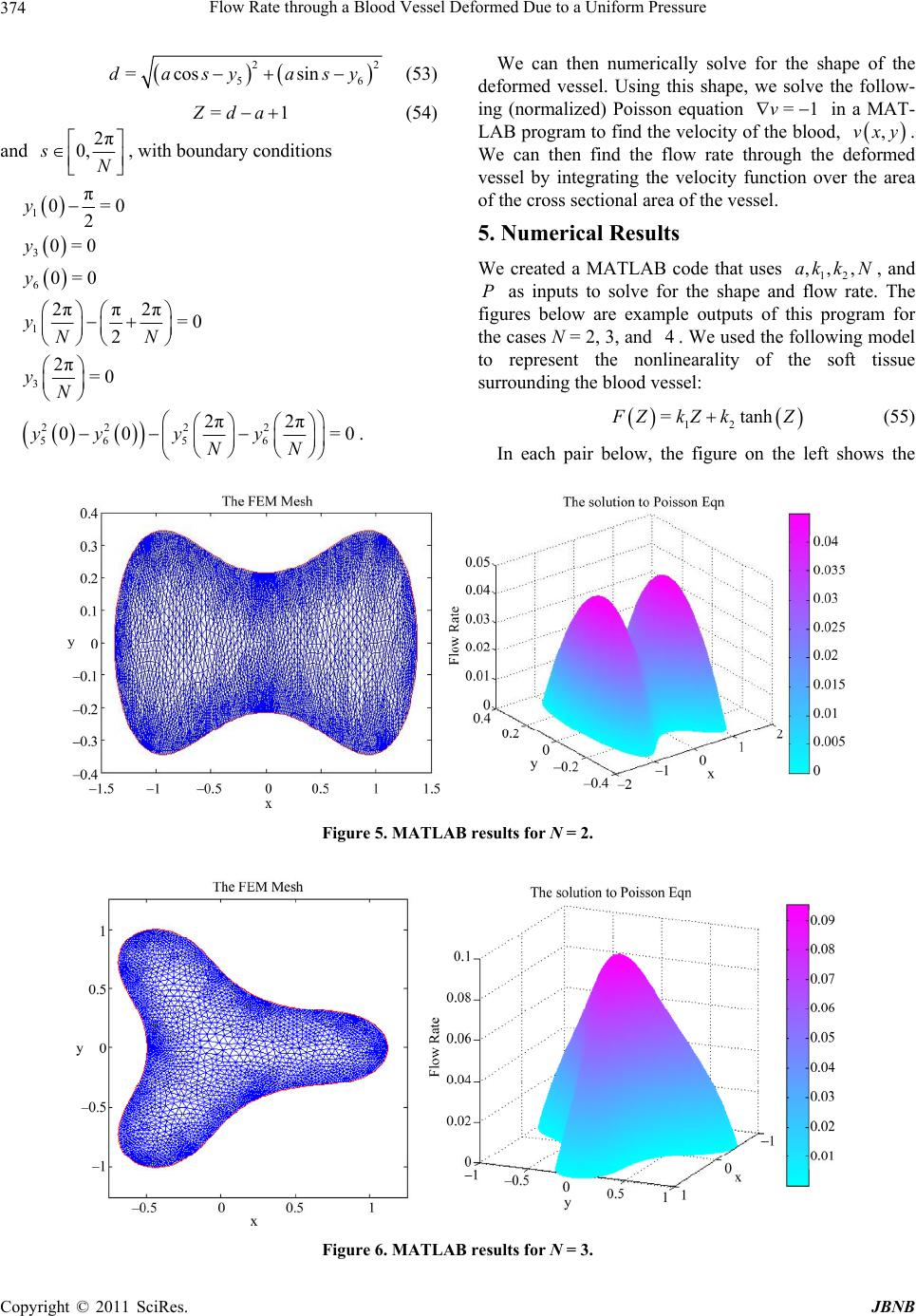

Flow Rate through a Blood Vessel Deformed Due to a Uniform Pressure 374

22
56
=cos sindasy asy  (53)
=1
Z
da

 (54)
and 2π 0,sN



, with boundary conditions

1
π
0=
2
y 0

30=0y

60=0 y
1
2ππ2π=0
2
yNN
 

 

3
2π=0yN





22 22
56 56
2π2π
00 =yy yy0
N

 
 
  
 

.
We can then numerically solve for the shape of the
deformed vessel. Using this shape, we solve the follow-
g (normalized) Poisson equation in a MAT-
A
in
L
=1v
B program to find the velocity of the blood,


,vxy.
We can then find the flow rate through the deformed
vessel by integrating the velocity function over the area
of the cross sectional area of the vessel.
5. Numerical Results
We created a MATLAB code that uses ,, ,ak kN, and
P as inputs to solve for the shape and fl
12
ow rate. The
this program
ollowing m
outputs of for figures below are example
the cases N = 2, 3, and 4. We used the fodel
to represent the nonlinearality of the soft tissue
surrounding the blood vessel:


12
tanh=
F
ZkZk Z (55)
In each pair below, the figure on the left shows the
N
Figure 5. MATLAB results for N = 2.
Figure 6. MATLAB results for N = 3.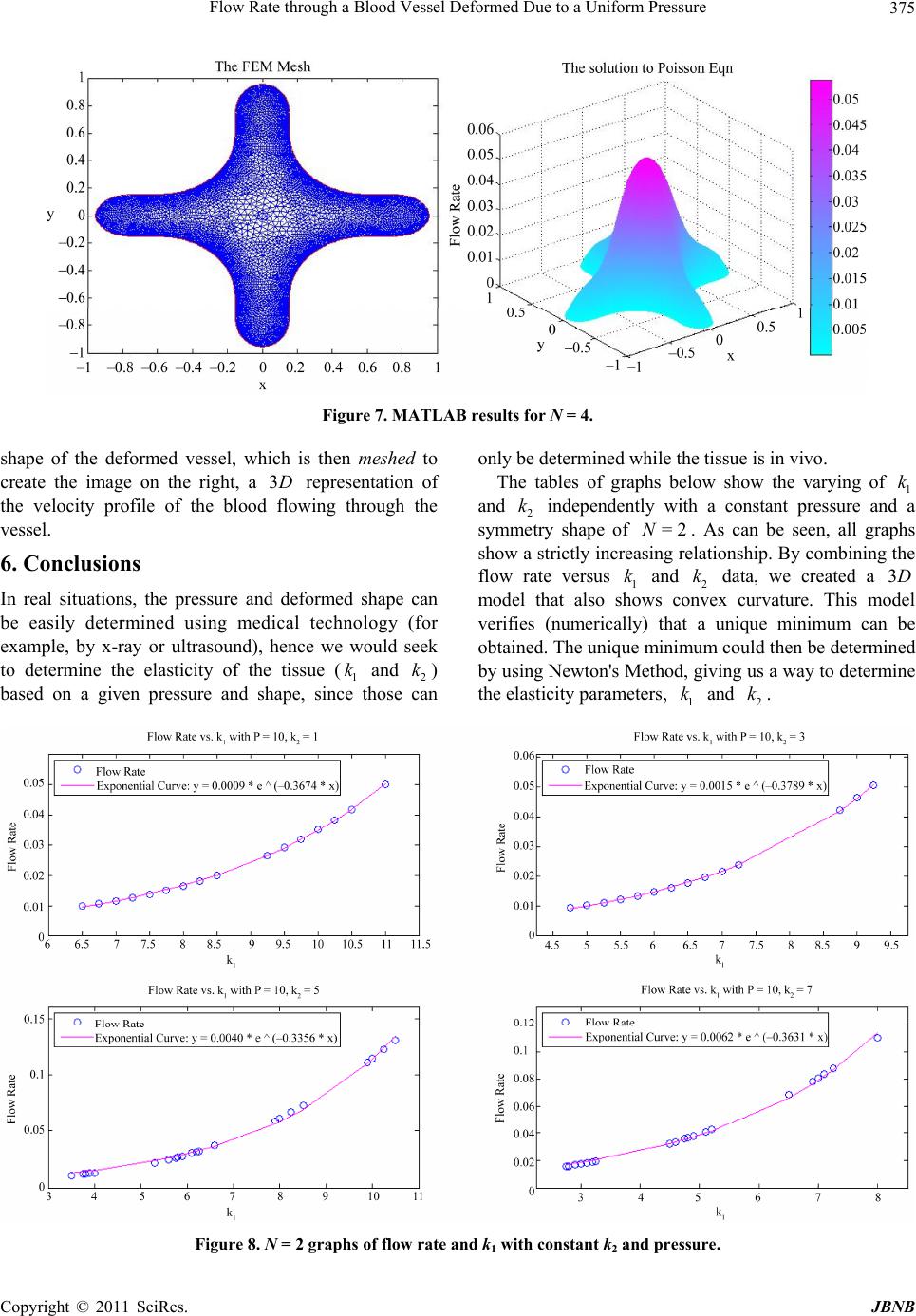

Flow Rate through a Blood Vessel Deformed Due to a Uniform Pressure375
Figure 7. MATLAB results for N = 4.
shape of the deformed vessel, which is then meshed to
create the image on the right, a representation of
the velocity profile of the blood flowing through the
vessel.
6. Conclusions
In real situations, the pressure and deformed shape can
be easily determined using medical technology (for
example, by x-ray or ultrasound), hence we would seek
to determine the elasticity of the tissue and)
based on a given pressure and shape, sin
only be determined while the tissue is in vivo.
The tables of graphs below show the varying of
and independently with a constant pressure an
sym ry shape of . As can be seen, all gra
show a strictly increalationship. By combining the
flowversus data, we created a
modat alsoex curvature. This m
verifiesnumericallynique minimum
obtaine The uni could then be determ
by Newton'ving us a way to determ
the elasticity param.
3D
(1 k
ce th
2 k
ose can
1
k
d a
phs
3D
odel
ined
ine
2
k
met
rate
el th
(
d.
using
=2N
sing re
1 and
ows conv
) that a
minim
Method, g
ters, 1 k
k
sh
que
s
e
2
k
u
um
i
and
can be
2 k
Figure 8. N = 2 graphs of flow rate and k1 with constant k2 and pressure.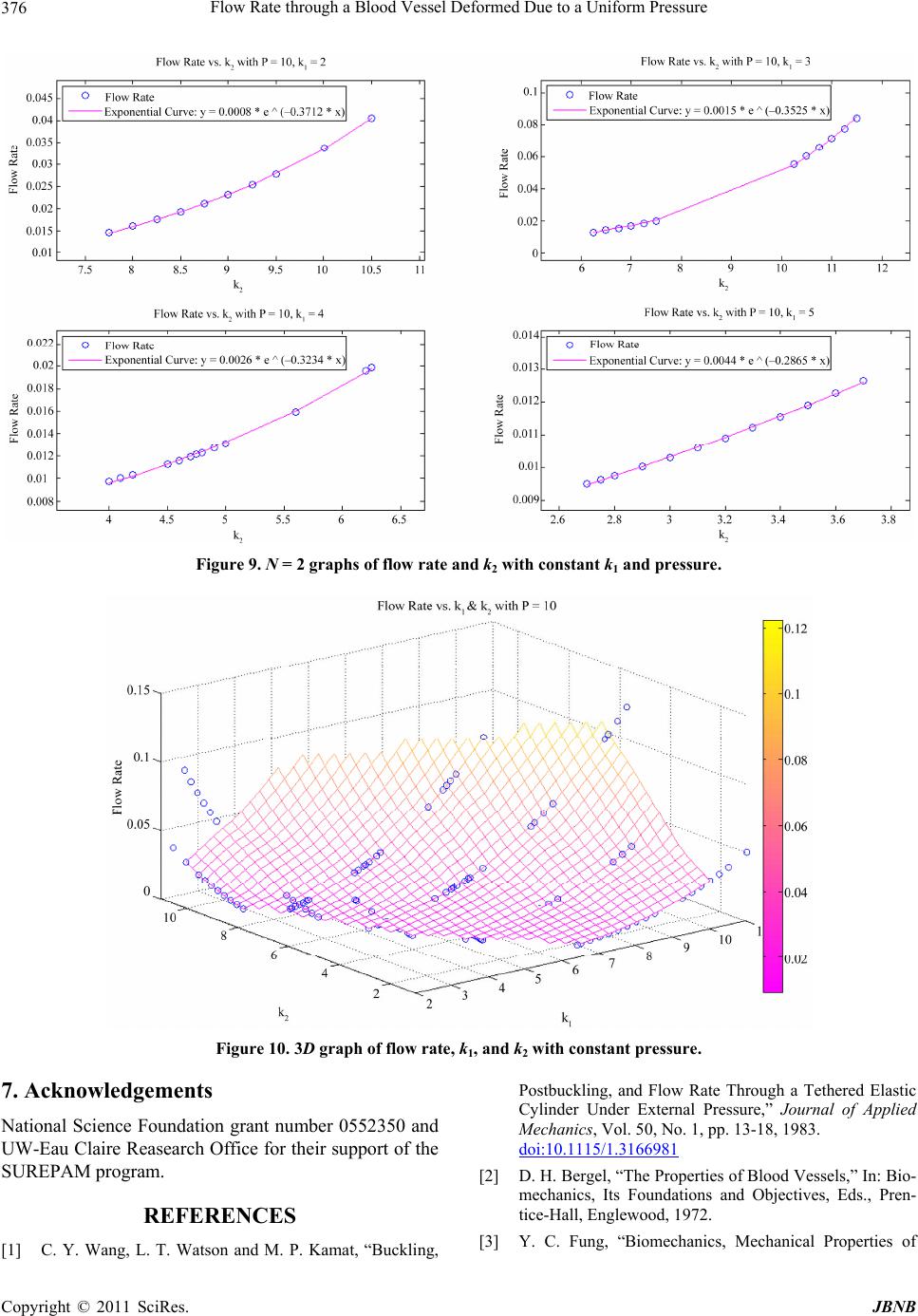

Flow Rate through a Blood Vessel Deformed Due to a Uniform Pressure 376
Figure 9. N = 2 graphs of flow rate and k2 with constant k1 and pressure.
Figure 10. 3D graph of flow ra te, k1, and k2 with constant pressure.
7. Acknowledgemen
nce Foundation grant number 0552350 and
UW-Eau Claire Reasearch Office for their support of the
SUREPAM program.
REFERENCES
[1] C. Y. Wang, L. T. Watson and M. P. Kamat, “Buckling,
ough a Tethered Elastic
Cylinder Under External Pressure,” Journal of Applied
Mechanics, Vol. 50, No. 1, pp. 13-18, 1983.
doi:10.1115/1.3166981
ts Postbuckling, and Flow Rate Thr
National Scie
[2] D. H. Bergel, “The Properties of Blood Vessels,” In: Bio-
mechanics, Its Foundations and Objectives, Eds., Pren-
tice-Hall, Englewood, 1972.
[3] Y. C. Fung, “Biomechanics, Mechanical Properties of
C
opyright © 2011 SciRes. JBNB

Flow Rate through a Blood Vessel Deformed Due to a Uniform Pressure377
Living Tissues,” Springer-Verlag, New York, 1990.
[4] A. C. Guyton and J. E. Hall, “Textbook of Medical Phy-
siology,” Saunders Company, 1996.
[5] A. H. Moreno, A. I. Katz, L. D. Gold and R. V. Reddy,
“Mechanics of Distension of Dog Veins and Other Very
Thin-Walled Tubular Sturctures,” Circulation Research,
Vol. 27, No. 6, 1970, pp. 1069-1080.
[6] K. Osterloch, P. Gaehtgens, and A. Pries, “Determination
of Microvascular Flow Pattern Formation in Vivo,” Ame-
rican Journal of Botany, Vol. 278, No. 4, 2000, pp.
H1142-H1152.
[7] J. Stoer and R. Bulirsch, “Introduction to Numerical
Analysis,” Springer-Verlag, New York, 1980.
[8] M. B. M. Elgindi, D. H. Y. Yen and C. Y. Wang, “De-
formation of a Thin-Walled Cylindrical Tube Submerged
in a Liquid,” Journal of Fluids and Structure, Vol. 6, No.
3, 1992, pp. 353-370.
doi:10.1016/0889-9746(92)90014-T