International Journal of Communications, Network and System Sciences
Vol.10 No.08(2017), Article ID:78386,10 pages
10.4236/ijcns.2017.108B011
The Improvement of Relay Selection Schemes in Two-Hop Cellular Networks
Hua Wu
School of Automotive Engineering, Beijing Geely University, Beijing, China




Received: May 17, 2017; Accepted: August 11, 2017; Published: August 14, 2017
ABSTRACT
In wireless networks, cooperative relaying could improve throughput by exploiting diversity. In order to reduce the amount of feedback for the channel gain, a semi-distributed scheme based on the relay feasible condition is proposed. Each relay node can measure its backward and forward channel gains. If both the channel gains are larger than a pre-defined threshold, this relay node is feasible. The final decision on the best relay selection is still given by the base station. Besides, the switch-and-examine relay selection scheme, which selects the first feasible relay node, is also investigated. Simulation results are presented to illustrate the advantage of two proposed schemes.
Keywords:
Relay Selection, Cooperative Relaying, Amplify-and-Forward, Cellular Networks

1. Introduction
In next-generation wireless networks, cooperative relaying can be applied to extend the coverage and mitigate the signal fading arising from multi-path propagation or blocks [1] [2] [3] [4] [5]. The main idea is that single-antenna mobiles in a multi-user scenario can “share” their antennas in a manner that creates a virtual multiple-input multiple-output (MIMO) system.
In [6], the authors have proposed a simple cooperative diversity method, which selects the best relay from available relays and then uses the best relay for cooperation between the source and the destination. This distributed relay selection method requires no topology information and is based on local measurements of the instantaneous channel conditions. Moreover, this scheme can achieve the same diversity-multiplexing tradeoff as achieved by more complex protocols [7] [8] [9], where coordination and distributed space-time coding for available relay nodes are required.
Generally, relay node selection in two-hop cellular networks [10] is much more manageable than that in ad hoc networks, mainly due to the presence of a central node (namely base station) with much more functionality and intelligence. Nevertheless, relay node selection is still a non-trivial issue in two-hop cellular networks since there will often be many candidate relay nodes for the source node and the failure to choose the optimal relay node would impair the overall performance improvement.
In [11], a centralized relay selection scheme is employed in the downlink of a cellular network. The base station uses the feedback to get the channel gain of every link. Then the base station calculates the available data rate through direct link (from base station to the mobile user) and triangular link (see in Figure 1) and determines the best link for each user. However, the channel gain feedback can cause a lot of burden to the system, and the base station applies the triangular link as long as the channel gain from the source node to the relay node is better than that of the direct link i.e.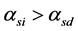 . The condition is not accurate.
. The condition is not accurate.
2. System Model
We consider the downlink in a cellular network with cooperative relaying. A single broadband channel is shared by all users in TDMA manner. The system under consideration consists of a source node, 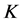 relay nodes, and
relay nodes, and  destination nodes. Throughout this paper, we consider half-duplex amplify-and- forward (AF) [3] relaying, where data transmission from the source to one destination requires two channel hops and two non-overlapping time slots. The transmission in the time domain is on a frame-by-frame basis. Each frame consists of two consecutive time slots. The link gain may integrate the effects from both propagation path loss and fading, and is varying independently among users, so that it is approximately unchanged during each frame interval.
destination nodes. Throughout this paper, we consider half-duplex amplify-and- forward (AF) [3] relaying, where data transmission from the source to one destination requires two channel hops and two non-overlapping time slots. The transmission in the time domain is on a frame-by-frame basis. Each frame consists of two consecutive time slots. The link gain may integrate the effects from both propagation path loss and fading, and is varying independently among users, so that it is approximately unchanged during each frame interval.
For simplicity, we firstly consider this case, the source node “s” transmits information to a destination node “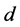 ” with the help of a relay node “
” with the help of a relay node “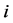 ”. In the first time slot, the source node transmits to the destination as well as the relay node. In this phase, the signals received at the destination and the relay are respectively given by
”. In the first time slot, the source node transmits to the destination as well as the relay node. In this phase, the signals received at the destination and the relay are respectively given by
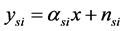 (1)
(1)
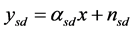 (2)
(2)
Figure 1. Cooperative relaying: triangular model.
where  denote the transmitted signal, the signal received at the destination and the signal received at the
denote the transmitted signal, the signal received at the destination and the signal received at the  relay node, respectively.
relay node, respectively. 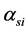 and
and  are channel coefficients of the source-relay and source-destination channels.
are channel coefficients of the source-relay and source-destination channels. 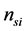 and
and 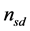 denote the background noise at the relay node
denote the background noise at the relay node 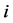 and destination node
and destination node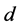 , respectively, which are independent identically distributed (i.i.d) complex Gaussian random variables with a common variance
, respectively, which are independent identically distributed (i.i.d) complex Gaussian random variables with a common variance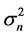 .
.
During the second time slot, while the source node is idle, the relay node amplifies and forwards its received signal from the source to the destination. The received signal at destination node 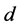 from relay node
from relay node 

where 



where 

3. Capacity Analysis of the Cellular Network with Cooperative Relaying
In this section, we analyze the capacity of the cellular network, which consists of one source, 

If 



where




Therefore, the maximum capacity would be attained when the relay with the largest 

which results in a capacity of

If no relaying is applied and both time slots in one frame contribute to the source node’s transmissions, the achievable average mutual information for the direct transmission can be calculated as

Next, the conditions for selecting a feasible relay node are considered. A relay node is feasible if user relaying via it can provide better capacity performance than direct transmission, that is,



where

We call the above condition “the relay feasible condition”. The condition for determining the feasibility of relay nodes ensures that user relaying via the node can achieve a larger channel capacity than direct transmission [12]. Moreover, the condition significantly reduces the search time for the best relay node. Note that we define the search time as the number of nodes searched during one execution of the search algorithm. As a result, the computational complexity can be effectively reduced. But in [11], the relay node is considered to be feasible as long as

Combining Equation (8) and Equation (9), the maximum average mutual information for a pair of cooperating users is equal to

maximum average mutual information for 

4. Two Proposed Relay Selection Schemes
4.1. Switch-and-Examine Relay Selection Scheme
Although the relay selection scheme in [6] can provide the multiplexing and diversity trade-off as distributed space-time coding, it may lead to the packet collision. In addition, all relay candidates must make works like the path estimations during every transmission which causes the power consumption of relay nodes. To overcome the issues, a sub-optimal relay selection scheme is proposed in [13], where the relay node is selected if its link quality is above a certain threshold which is set to satisfy the required performance and the selected link is maintained unless its link quality does not fall below the threshold. Note that the relay nodes work at Decode-and-Forward (DF) mode in [13].
Nevertheless, in the scheme in [13], there is no exact definition about the target threshold. Moreover, if the first 


We assume there are 






Figure 2. The block diagram of the modified switch-and-examine relay selection scheme.
As can be seen from the above scheme, setting the target threshold as 
4.2. The Semi-Distributed Relay Selection Scheme
As analyzed above, switch-and-examine relay selection scheme is a distributed scheme in which each relay can make decision on its feasibility individually. However, this scheme can’t maximize the system capacity because the selected relay is not optimal and it is the first one which satisfies the condition (i.e. 

In order to deal with above problems, we propose a semi-distributed relay selection scheme for the downlink of cellular networks. The proposed relay selection scheme can be described as follows.
Step 1. The decision method of feasible set is the same as the idea of [12]. Before a source node initiates packet transmission to the destination, some hand-shaking signals have to be exchanged, such as request to send (RTS) and CTS in ad hoc networks. Similarly, some pilot signals need to be exchanged in cellular networks before data transmission. We borrow the names RTS and CTS to represent the hand-shaking signals before data transmission. After receiving the RTS, the destination node estimates the channel gain, 


Step 2. The relay nodes, who received both RTS and CTS, can estimate the channel gain, 




Step 3. After receiving all notifications from the feasible relay nodes, the source node generates a feasible set for each destination node. The source node sorts the destination nodes in ascending order based on the estimates of 
Step 4. For a given destination node, the relay node which has the maximal 
Step 5. The source node removes the selected destination node’s feasible set and removes the selected relay node from all feasible sets.
Step 6. The source node repeats the previous steps until there is no non- zero feasible set. The source node broadcasts the relay node allocation to all nodes. Then it will start data transmission.
Based on the above procedure of relay selection, we see that the proposed semi-distributed scheme can achieve higher capacity than that of the relay selection scheme in [12]. This is due to the fact that for the scheme in [12], one relay node is randomly chosen from each destination’s feasible set, but for the proposed scheme, the optimal relay node which can help the source to achieve the maximal capacity is selected from the feasible set. Moreover, in this relay selection scheme, each relay node can determine its feasibility according to the threshold 
5. Simulation Results
In this section, we first compare the switch-and-examine relay selection scheme with the scheme in [13]. Consider a circle centered at the origin of the 



Firstly, we consider a simple case composed of one source node, 99 relay nodes and one destination node. The destination is located at the edge of the coverage area and the relay nodes are uniformly distributed in the circle. Figure 3 shows the performance comparison of the switch-and-examine relay selection
Figure 3. Performance comparison of switch-and-examine relay selection scheme and the scheme in [13].
scheme and the scheme in [13]. With the increase of transmit SNR, switch-and- examine relay selection scheme always gains higher average mutual information than that with the scheme in [13].
Figure 4 illustrates average mutual information versus the transmit SNR of five relay selection schemes. It can be shown that the proposed semi-distributed scheme gains higher capacity than the relay selection scheme in [12] and switch-and-examine scheme. This verifies the analysis in Section IV. Besides, it can be found that the semi-distributed scheme gets almost equivalent capacity with that of the scheme in [11]. Figure 4 also shows that the direct transmission has relatively poor performance than other schemes. This is because direct transmission does not benefit from cooperative diversity at high SNR.
Figure 5 shows the proposed scheme exhibits better average search time for the best relay than that of the scheme in [11]. For instance, at SNR = 40 dB, the average search time using the proposed scheme is nearly one sixth of those using the scheme in [11]. Combining Figure 4 with Figure 5, we can observe that the semi-distributed relay selection scheme provides the same capacity gains with the scheme in [11], but need much lower computational complexity than the scheme in [11].
Figure 6 shows the case with multiple destination nodes. The source is located at the center and other 100 nodes are uniformly distributed in the circle. One half of the 100 nodes are chosen as the destination nodes and the other half are considered as the relay nodes. It can be found that the semi-distributed scheme outperforms other schemes.
6. Conclusion
In this paper, we propose a semi-distributed relay selection scheme on the relay
Figure 4. Average mutual information of five relay selection schemes with different SNR (one destination).
Figure 5. Computational complexity of two relay selection schemes with different SNR.
Figure 6. Total average mutual information of different relay selection scheme.
feasible condition for the downlink of cellular networks. Simulation results show that the semi-distributed scheme can achieve the nearly equivalent capacity compared with the scheme in [11], but the former has significantly reduced computational complexity. We also discuss the switch-and-examine relay selection scheme, which can reduce the complexity and power consumption at the relays. Simulation results validate our analysis and show that the semi-distri- buted scheme outperforms the switch-and-examine scheme. Besides, the two relay selection schemes can achieve much more capacity than direct transmission at high SNR because direct transmission does not benefit from cooperative diversity.
Acknowledgements
The research work was supported by Science Research project of Beijing Geely University under Grant No. 2016YB0302.
Cite this paper
Wu, H. (2017) The Improvement of Relay Selection Schemes in Two-Hop Cellular Networks. Int. J. Communications, Network and System Sciences, 10, 98-107. https://doi.org/10.4236/ijcns.2017.108B011
References
- 1. Fitzek, F.H.P. and Katz, M.D. (2006) Cooperation in Wireless Networks: Principles and Applications. Springer, Netherlands. https://doi.org/10.1007/1-4020-4711-8
- 2. Scaglione, A., Goeckel, D. and Laneman, J.N. (2006) Cooperative Communi-cations in Mobile Ad Hoc Networks: Rethinking the Link Abstraction. IEEE Signal Pro- cessing Magazine, 23, 18-19. https://doi.org/10.1109/MSP.2006.1708409
- 3. Laneman, J.N., Tse, D.N.C. and Wornell, G.W. (2004) Cooperative Di-versity in Wireless Networks: Efficient Protocols and Outage Behavior. IEEE Transactions on Information Theory, 50, 3062-3080. https://doi.org/10.1109/TIT.2004.838089
- 4. Sendonairs, A., Erkip, E. and Aazhang, B. (2003) User Co-operation Diversity-Part I: System Description. IEEE Transactions on Communications, 51, 1927-1938. https://doi.org/10.1109/TCOMM.2003.818096
- 5. Sendonairs, A., Erkip, E. and Aazhang, B. (2003) User Cooperation Diversity-Part II: Implementation Aspects and Performance Analysis. IEEE Transactions on Com- munications, 51, 1939-1948. https://doi.org/10.1109/TCOMM.2003.819238
- 6. Bletsas, A., Khisti, A., Reed, D.P. and Lippman, A. (2006) A Simple Cooperative Diversity Method Based on Network Path Selection. IEEE Journal on Selected Areas in Com-munications, 24, 659-672. https://doi.org/10.1109/JSAC.2005.862417
- 7. Laneman, J.N. and Wornell, G.W. (2003) Distributed Space-Time-Coded Protocols for Exploiting Cooperative Diversity in Wireless Networks. IEEE Transactions on Information Theory, 49, 2415-2425. https://doi.org/10.1109/TIT.2003.817829
- 8. Jing, Y. and Hassibi, B. (2006) Dis-tributed Space-Time Coding in Wireless Relay Networks. IEEE Transactions on Wireless Communications, 5, 3524-3536. https://doi.org/10.1109/TWC.2006.256975
- 9. Stefanov, A. and Erkip, E. (2005) Cooperative Space-Time Coding for Wireless Net- works. IEEE Transactions on Communications, 53, 1804-1809. https://doi.org/10.1109/TCOMM.2005.858641
- 10. Sreng, V., Yanikomeroglu, H. and Falconer, D.D. (2003) Relayer Se-lection Strategies in Cellular Networks with Peer-to-Peer Relaying. Proceedings of 2003 IEEE 58th Vehicular Technology Conference, Orlando, 6-9 October 2003, 1949-1953. https://doi.org/10.1109/VETECF.2003.1285365
- 11. Song, S., Son, K., Lee, H.W. and Chong, S. (2007) Opportunistic Relaying in Cellular Network for Capacity and Fairness Improvement. Proceedings of IEEE Global Telecommunications Con-ference, Washington, DC, 26-30 November 2007, 4407-4412. https://doi.org/10.1109/GLOCOM.2007.838
- 12. Cai, J., Shen, X., Mark, J.W. and Alfa, A.S. (2008) Semi-Distributed User Relaying Algorithm for Amplify-and-Forward Wireless Relay Networks. IEEE Transactions on Wireless Communications, 7, 1348-1357. https://doi.org/10.1109/TWC.2008.060909
- 13. Hwang, K.-S. and Ko, Y.-C. (2007) Switch-and-Examine Node Selection for Efficient Relaying Systems. Proc. IWCMC’07, Honolulu, Hawaii, 469-474.







