Optics and Photonics Journal
Vol.07 No.08(2017), Article ID:78312,11 pages
10.4236/opj.2017.78B016
Design of 1.33 μm and 1.55 μm Wavelengths Quantum Cascade Photodetector
S. Khosravi1, A. Rostami1,2
1Photonics and Nanocrystal Research Lab. (PNRL), Faculty of Electrical and Computer Engineering, University of Tabriz, Tabriz, Iran
2SP-EPT Labs., Industrial Park of Advanced Technologies, Tabriz, Iran




Received: June 9, 2017; Accepted: August 7, 2017; Published: August 10, 2017
ABSTRACT
In this paper, a quantum cascade photodetector based on intersubband transitions in quantum wells with ability of detecting 1.33 μm and 1.55 μm wavelengths in two individual current paths is introduced. Multi quantum wells structures based on III-Nitride materials due to their large band gaps are used. In order to calculate the photodetector parameters, wave functions and energy levels are obtained by solving 1-D Schrodinger?Poisson equation self consistently at 80 ˚K. Responsivity values are about 22 mA/W and 18.75 mA/W for detecting of 1.33 μm and 1.55 μm wavelengths, respectively. Detectivity values are calculated as 1.17 × 107 (Jones) and 2.41 × 107 (Jones) at wavelengths of 1.33 μm and 1.55 μm wavelengths, respectively.
Keywords:
Quantum Cascade Photodetector, III-Nitride Multi Quantum Well, Responsivity and Detectivity

1. Introduction
Quantum well infrared photodetectors (QWIPs) as thermal imagers using focal plane arrays (FPAs) have been studied extensively [1] [2] [3]. For electronic transport QWIPs operate at photoconductive and photovoltaics modes. Applications of QWIPs at photoconductive mode are limited at low temperature because of existence an external applied bias. QWIPs based on photovoltaic mode are promising devices operating in high temperature and longer wavelength applications because of having no external voltage bias and dark current [4]. Quantum cascade detectors (QCDs) operating in photovoltaics mode are promising devices for small pixel large area FPAs, multicolor detection and demultiplexers [5]. A typical QCD consist of an active region constructed of multiple periods, each containing a thick, highly doped active QW and a nominally undoped extraction cascade composed of thinner QWs. The electrons in the ground state of doped wells in each period are excited to the upper level, then extract from this well by emission of an optical phonon. The speed of detectors based on intersubband transition (ISBT) is limited by the electron ISBT scattering time is about 1 ps [3]. Conduction-band ISBT QCDs operate based on photon?electron interactions between quantized subbands in the conduction band of wells. In QCD structure Multi quantum wells (MQWs) are designed dependant on detected wavelengths [6] [7] [8] [9] [10]. For small wavelength, quantum well structures with small conduction band offset such as GaAs/AlGaAs and InGaAs/InAlAs are used [5] [6] [7]. MQWs based on III-Nitride materials due to large conduction band offset and large LO-phonon energy are the best candidate for design of UV and NIR photodetector [11] [12] [13] [14] [15]. In the other hand, 1.33 μm and 1.55 μm wavelengths are interest, because of their importance in optical fiber communications. Attenuation of fiber glass at 1.55 μm wavelength is minimal so, this wavelength useful for long distance communication. Also, distortion of optical signal centered at 1.33 μm wavelength is minimal.
In this paper, a QCD for detecting of 1.33 μm and 1.55 μm wavelengths in individual current paths based on intersubband transitions in AlGaN/AlN MQWs is designed. Paths are separated by 100 Å AlN In order to calculate photodetector parameters, wave functions and energy levels are obtained by solving 1-D Schrodinger?Poisson equation self consistently at 80˚K. Incident wavelength excite the electrons populated the first energy level of n+ doped QWs, after that they are extracted from first wells by emitting optical phonons emission having energy close to GaN LO-phonon energy (92 meV). Responsivity of paths is about 22 mA/W and 18.75 mA/W for detecting of 1.33 μm and 1.55 μm wavelengths respectively. Detectivity values are calculated as 1.17 × 107 (Jones) and 2.41 × 107 (Jones) at wavelengths of 1.33 μm and 1.55 μm respectively.
2. Theoretical Background and Simulation Results
A 3D view of the design QCD with ability of detection 1.33 μm and 1.55 μm wavelengths in two separated paths is indicated in Figure 1.
Each path separated by 100 Å AlN. Paths 1 and 2 are designed for detection of 1.33 μm and 1.55 μm wavelengths, respectively. They possess 20 periods AlxGa1−xN/AlN MQWs, the thickness of barriers and wells listed in Table 1 and Table 2. The first QWs in each path are n+ doped with concentration of 5 × 1011 cm−2. Conduction band edge and wave functions for each path are shown in Figure 2. As shown in Figure 2, by incoming radiation, the photoexcited electrons transport to the lower energy levels with optical phonons emission close to GaN LO-phonon energy (92 meV) until reach the first levels in the next period of the path.
Figure 1. A 3D view of the design QCD with ability of detection 1.33 μm and 1.55 μm wavelengths in two separated paths.
Table 1. Path1 with 20 periods MQWs for detection 1.33 μm.


Figure 2.. Conduction band edge and wave functions for each path for detection of (a) 1.33 μm and (b) 1.55 μm.
Table 2. Path 2 with 20 periods MQWs for detection 1.55 μm.
The wave functions are calculated by solving 1-D Schrodinger-Poisson self consistently at 80 ˚K [16]. For conduction band edges calculation pyroelectric and piezoelectric polarization effects in III-Nitrid materials are considered [17]. Internal electric field due to polarization effects in jth layer for a k layers quantum structures is obtained as Equation (1) [18]:
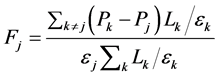 (1)
(1)
where, j and k are the number of layers. Lk, Pk, Pj, εj and εk are the length of layers, the total polarization and permittivity of jth and kth layer, respectively.
The absorption coefficient is obtained as Equation (2) [10]:
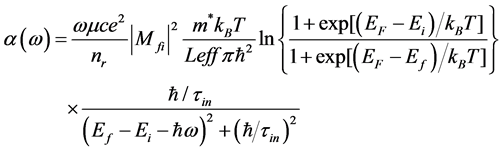 (2)
(2)
where, Ei and Ef, are the quantized energy levels for the initial and final states, respectively. Mfi, μ, c, Leff, nr and τin are dipole matrix element between initial and final states, the permeability, the speed of light in free space, the effective spatial extent of electrons in subbands, the refractive index and the intersubband relaxation time respectively. The absorption coefficient at 80˚K for each path is indicated in Figure 3.
Absorption coefficient is linked to dipole matrix element between initial and final states through Equation (2). As illustrated the path for detection of 1.55 μm has small absorption coefficient due to the small overlapping of wave functions between initial and first levels.
Figure 3. Absorption coefficient for paths versus incident wavelength at 80 ˚K.
The responsivity R for each path is obtained as Equation (3) [3]:
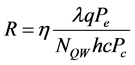 (3)
(3)
where, λ, c, q, h, η, Pe, Pc, NQW are the incident wavelength, the speed of light in free space, the elementary charge, Planck’s constant, the quantum efficiency, the escape probability of an excited electron in active QW, capture probability into the active QW’s ground state for an electron traveling down the QCD’s cascade and the number of active QW periods of the QCD. Absorption efficiency is expressed as Equation (4) [3]:
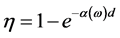 (4)
(4)
where, α and d are the absorption coefficient and thickness of active well in each period, respectively. The responsivity for each path at 80 ˚K is indicated in Figure 4.
In QCDs, resistance of the one period of the structure at zero bias in area of the device defined as R0A, is an important parameter characterized the dark current (current in absence of incident light) [4]. In order to calculate the R0A only interaction between electrons and LO-phonon is considered and interaction between electrons and acoustical phonons are neglected due to sufficient high differences between the energy levels in the studied structures [4]. R0A is obtained as Equation (5) [4]:
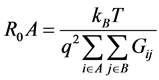 (5)
(5)
Here, Gij is global transition rate between the subband i and subband j and is the sum of the two transition rates for absorption of LO phonons (Gaij), and
Figure 4. Responsivity for each path versus incident wavelength at 80 ˚K.
emission of LO phonons (Geij) [4]. For one period of each path R0A as a function of 1000/T is shown in Figure 5. To obtain the total resistance in area (R0A) the values in Figure 5 must be multiplied in numbers of periods. As shown in Figure 5, R0A for path 1 has lower values than R0A of path 2 due to higher transition rates values as described in the following. Dominant global transition rates between first energy level and other subbands in one period for paths are indicated in Figure 6.
Dominant transition rates values at temperatures of 80 ˚K, 120 ˚K and 240 ˚K for instances for paths 1 and 2 are listed in Table 3 and Table 4, respectively.
As observed in Table 3 and Table 4 since global transition rates of path 1 are higher than the values for path 2 so, the resistance at null bias of path 1 is lower. Higher global transition rates between two levels can be related to higher overlapping of corresponding wave functions [3]. For path 1 this overlapping is high
Figure 5. R0A versus 1000/T (T is structure temperature).
Table 3. Dominant transition rates of path1 at three different temperatures.
Table 4. Dominant transition rates of path 2 at three different temperatures.


Figure 6. Dominant global transition rates for paths (a) 1 and (b) 2.
(due to having smaller width of the wells) which leads to smaller resistance values. Electron transition capability between two levels is increased by increasing temperature, therefore as shown in Table 3 and Table 4, by increasing sample temperature the global rates is increased.
Detectivity for the designed detector is limited by Johnson-noise obtained as Equation 6 [3]:
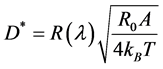 (6)
(6)
where, R(λ), R0A are the responsivity spectrum and resistance of device in area of the device, respectively. Detectivity versus incident wavelength for paths at 80 ˚K is shown in Figure 7.
Paths have difference detectiveity values due to having different responsivity and resistivity (at zero bias) values shown in Figure 4 and Figure 5, respectively.
Figure 7. Detectivity spectrum for paths at 80 ˚K.
3. Conclusion
In this research, a QCD for detecting of 1.33 μm and 1.55 μm wavelengths in individual current paths based on intersubband transitions in AlGaN/AlN MQWs was designed. In order to calculate photodetector parameters, 1-D Schrodinger? Poisson equation self consistently at 80˚K was solved to obtain wave functions and energy levels. Responsivity values about 22 mA/W and 18.75 mA/W for detecting of 1.33 μm and 1.55 μm wavelengths, respectively. Detectivity values are calculated as 1.17 × 107 (Jones) and 2.41 × 107 (Jones) at wavelengths of 1.33 μm and 1.55 μm, respectively.
Acknowledgements
This work is supported by Photonics and Nanocrystal research Lab. (PNRL), Faculty of Electrical and Computer Engineering of Tabriz University and SP- EPT Labs., ASEPE Company, Industrial Park of Advanced Technologies, Tabriz, Iran.
Cite this paper
Khosravi, S. and Rostami, A. (2017) Design of 1.33 μm and 1.55 μm Wavelengths Quantum Cascade Photodetector. Optics and Photonics Jour- nal, 7, 116-126. https://doi.org/10.4236/opj.2017.78B016
References
- 1. Dupont, E., Byloos, M., Gao, M., Buchanun, M., Song, C.Y., Wasilewski, Z.R. and Liu, H.C. (2002) Pixelless Thermal Imaging with Integrated Quantum Well In-frared Photodetector and Light Emitting Diode. IEEE Photonics Technology Let-ters, 14, 182-184. https://doi.org/10.1109/68.980504
- 2. Levine, B.F. (1993) Quantum Well Infrared Photodetectors. J. Appl. Phys, 74, R1- R76. https://doi.org/10.1063/1.354252
- 3. Giorgetta, F.R., Baumann, E., Graf, M., Yang, Q., Manz, C., Kohler, K., Beere, H.E., Ritchie, D.A., Linfield, E., Davies, A.G., Fedoryshyn, Y., Fischer, Jackel, H., Faist, J. and Hofstetter, D. (2009) Quantum Cascade Detectors. IEEE Journal of Quantum Electronics, 8, 1039-1052. https://doi.org/10.1109/JQE.2009.2017929
- 4. Koeniguer, C., Dubois, G., Gomez, A. and Berger, V. (2006) Electronic Transport in Quantum Cascade Structures at Equilibrium. Phys. Rev. B., 74. https://doi.org/10.1103/PhysRevB.74.235325
- 5. Rostami, A., Oliaee Re-zayee, R., Rasooli Saghai, H., Yadipour, R. and Baghban, H. (2010) A Dual-Color IR Quantum Cascade Photodetector with Two Output Electrical Signals. IEEE Transaction on Electron Devices, 58, 165-172. https://doi.org/10.1109/TED.2010.2082546
- 6. Giorgetta, F.R., Baumann, E., Theron, R., Pellaton, M.L., Hofstetter, D., Fischer, M. and Faist, J. (2008) Short Wavelength (4μm) Quantum Cascade Detector Based on Strain Compen-sated InGaAs/InAlAs. Appl. Phys. Lett, 92. https://doi.org/10.1063/1.2902301
- 7. Graf, M., Hoyler, N., Giovannini, M., Faist, J. and Hofstetter, D. (2008) InP-Based Quantum Cascade Detectors in the Mid-Infrared. Appl .Phys. Lett, 88.
- 8. Giorgetta, F.R., Baumann, E., Graf, M., Ajili, L., Hoyler, N., Giovannini, M., Faist, J., Hofstetter, D., Krotz, P. and Son-nabend, G. (2007) 16.5 μm Quantum Cascade Detector Using Miniband Transport. Appl .Phys. Lett, 90.
- 9. Mei, T., Karunasiri, G. and Chua, S.J. (1997) Two-Color Infrared Detection Using Intersubband Transitions in Multi-ple Step Quantum Wells with Superlattice Barriers. Appl. Phys. Lett., 71.
- 10. Ozturk, E. and Sokmen, I. (2003) Intersubband Transitions for Single, Double and Triple Si δ-Doped GaAs Layers. Appl. Phys, 36. https://doi.org/10.1088/0022-3727/36/20/006
- 11. Hofstetter, D., Bau-mann, E., Giorgetta, F.R., Theron, R., Wu, H., Schaff, W.J., Dawlaty, J., George, P.A., Eastman, L.F., Rana, F., Kandaswamy, P.K., Leconte, S. and Monroy, E. (2010) Intersubband Transition-Based Processes and Devices in AlN/ GaN-Based Heterostructures. Proceedings of the IEEE, 7. https://doi.org/10.1109/JPROC.2009.2035465
- 12. Hofstetter, D., Baumann, E., Giorgetta, F.R., Theron, R., Wu, H., Schaff, W.J., Dawlaty, J., George, P.A., Eastman, L.F., Rana, F., Kandaswamy, P.K., Leconte, S. and Monroy, E. (2009) Photodetectors Based on Intersubband Transitions Using III- Nitride Superlat-tice Structures. J. Phys.: Condens. Matter, 21. https://doi.org/10.1088/0953-8984/21/17/174208
- 13. Zhanga, S.K., Wang, W.B., Yun, F., He, L., Morkoc, H., Zhou, X., Tamargo, M. and Alfano, R.R. (2002) Backilluminated Ultraviolet Photodetector Based on GaN/AlGaN Multiple Quantum Wells. Appl. Phys. Lett, 24. https://doi.org/10.1063/1.1527994
- 14. Teke, A., Dogan, S., Yun, F., Resh-chikov, M.A., Le, H., Liu, X.Q., Morkoc, H., Zhang, S.K., Wang, W.B. and Alfano, R.R. (2003) GaN/AlGaN Back-Illuminated Multiple-Quantum-Well Schottky Bar-rier Ultraviolet Photodetectors. Solid-State Electronics, 47. https://doi.org/10.1016/S0038-1101(03)00068-6
- 15. Chen, G., Wang, X.Q., Rong, X., Wang, P., Xu, F.J., Tang, N., Qin, Z.X., Chen, Y.H. and Shen, B. (2015) Intersubband Transition in GaN/InGaN Multiple Quantum Wells. Nature, Sci-ence Report.
- 16. Rostami, A., Baghban, H. and Rasooli Saghai, H. (2007) An Ultra-High Level Second-Order Nonlinear Optical Susceptibility in Strained Asymmetric GaN-AlGaN- AlN Quantum Wells: Towards All-Optical Devices and Systems. Microelectronics Journal, 38, 900-904. https://doi.org/10.1016/j.mejo.2007.07.071
- 17. Galczak, J., SarzaLa, R.P. and Nakwaski, W. (2004) Spatial Separation of Recombining Carriers within Ni-tride GaN/(AlGa)N Quantum Wells Induced by Piezoelectric Phenomena. Opto-Eelectron. Rev., 12, 369.
- 18. Li, Y. and Paiella, R. (2006) Intersubband All-Optical Switching Based on Coulomb-Induced Optical Nonlinearities in GaN/AlGaN. Semicond. Sci. Technol., 21, 1105. https://doi.org/10.1088/0268-1242/21/8/022







