ABSTRACT

The optimal acousto-optic interaction length in Raman-Nath diffraction is investigated by using deliberately designed apparatus working with pure water. Then the optimum interaction length, the suitable dimensions of the transducer, and the required index difference dominated by the ultrasonic frequency and power for achieving the ultimate efficiency are analyzed. The portable device analogy to the solid appliance is designed based on the optimization. Taking advantage of the device the highest diffraction efficiency of more than 98% is obtained. The feasibility of using the portable device to act as a Q-switch for ultraviolet and visible lasers is discussed.

Keywords:

Raman-Nath Diffraction, Optimum Interaction Length, Ultimate Diffraction Efficiency

1. Introduction

The features of Raman-Nath (R-N) acousto-optic diffraction are with short interaction length and multi-order diffraction. The distribution of the energy in each diffractive order follows Bessel function [1]. It is significant that the zero order term, J₀(φ), of Bessel function is equal to zero while the synthetics φ takes the values of 2.405, 5.520….. This manifests that the zero order diffraction (the incidence passed the acousto-optic medium) would become a dark field and all the energy is diffracted into all the other orders. In this case the total diffractive efficiency attains to 100%. However, so far, such a high efficiency has not been reported. Recent years most of researchers pay their attentions to Braggs’ devices and their applications, which has a sole diffractive beam (e.g. [2] [3] [4]). And only a few of them studies to R-N diffraction [5] because its energy disperses into the multi-order diffractions. However, if considering the zero order can vanish at the ultimate efficiency, it predicts that taking advantage of the zero order diffraction and the short interaction length of R-N regime a portable Q-switch device is feasible at the ultimate efficiency.

In this paper the apparatus working with pure water for studying the interaction length is designed first. The optimum interaction length and the dimensions of the transducer against the ultrasonic for achieving the ultimate efficiency are analyzed. Based on the analyses, the portable device analogy to the solid appliance is designed. The highest diffractive efficiency of more than 98% is achieved with the portable device. Finally, the feasibility of the portable device acting as a Q-switch for ultraviolet and visible lasers is discussed.

2. Experimental Apparatus

Without putting the sheet of foam, or the medium is driven by standing sound wave. The multi-order diffraction is occurred as Figure 1.

A glass tank sized 80 × 60 × 60 mm and filled of pure water in depth of 2/3 the tank is taken as the acousto optical cell. The transducer-head with heat radiator sat on an adjustable mechanism which can be slide along the trail mounted on the upper frame of the water tank, see Figure 1. The head is inserted uprightly into the water. The transducer sized 20 × 10 × 0.2 mm³, which is driven by the homemade ultrasonic generator. (The largest acoustic power to be fed into the transducer is about 5 watts) The ration of standing wave is less than 1:1.2. A He-Ne laser (632.8 nm) and a CW Nd: YAG/KTP laser (532 nm) are employed as the light sources. The incidence is adjusted to be 3 - 5 mm beneath the transducer.

To measure the interaction length between the sound and the light, an aluminum block with a hole of φ₃ mm is deliberately put in the sound field and beneath the transducer-head to cut off the field. The diffracted beam can run through the hole and is received by the photo diode. The initial position of the fore-rim of the transducer, P₀, aims exactly to the fore-surface of the aluminum block. In this case the laser is shielded from the sound field by the aluminum block. Starting from P₀ the head is drawn to slide forward against the block so that the laser could enter the sound field. Through carefully adjusting the orientation of the transducer to make it nearly normal incidence, it is found that no

sooner the laser enter the sound field than the diffraction generated. While the head is drawn step be step the intensity of the diffracted beam was recorded. Then the diffractive intensity as a function of the interaction length is obtained. For avoiding disturbance from the sound a thin layer of porous material is covered on the aluminum block to absorb the sound.

3. Results Analysis

When applying the sound wave with the frequency of f_s~10 MHz and the power of ~1 W, the diffractive efficiency, up to the third order, as the function of the interaction length are measured. Here, the data of the first order is taken and listed in Figure 2. It is apparently that the transverse coordinates, or the interaction length, of all the peaks of the curves, are almost at the same scale of ~8 mm. This shows that the optimum interaction length is ~8 mm in this case.

In terms of the experimental results, the portable Q-switch working with pure water is designed as the photo in Figure 3. The body of the switch is made of aluminum with the dimensions of 40 × 40 × 17 mm³. The transducer volume is 8 × 0.2 mm³. The ration of standing wave for the electric network to feed the supersonic is practically designed to the less than 1:1.2.

In order to observe the process evolving toward the ultimate efficiency, applying the supersonic with frequency of ~10 MHz to the portable device, the

patterns of the diffractive spots with a He-Ne laser at different supersonic power are photographed as Figure 4. The diffractive angle is measured as θ = 3.1 mrad.

Bessel terms, J_m(φ), represent the diffraction efficiency of mth order. Here, the acousto-optic synthesis, or the phase of the diffractive wave [1],

(1)

where λ₀ is the wavelength of the incidence. n is the index. L is the interaction length. And Δn is the index difference, which can be expressed by

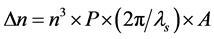(2)

With P is the photoelastic coefficient. λ_s is the supersonic wavelength. A is the amplitude of the medium driven by the sound.

Figure 4(a) is shot at the power of 1 W. In this case the device is working at a little bit warmer than the room temperature. The efficiency of the +1th or −1th is measured as 27%. Converting it into Bessel term, corresponding to J₁(φ) = 0.52 for φ = 1.25. Then J₀(φ) = 0.65, or the efficiency of the zero-order is [J₀(φ)]² = 42%. Indeed the energy in the zero spot is tested as about 0.4 of the incidence.

Figure 4(b) is at 2.5 W, which amplitude should be 1.58 times of case (a). Taking advantage of Equations (1) and (2), φ =1.25 × 1.58 = 1.98, then, the efficiency of the first order is [J₁(φ)]² = 33.4%. The zero-order is [J₀(φ)]² = 5.8%. In this case the first order almost approaches to the maximum as the theory predicts. The zero-order turns to dark.

As the power is increased to 3.4 W, for Figure 4(c), φ = 1.17 × 1.98 = 2.32. In this case the energy remains in the zero-order is only 0.3% of the incidence. Indeed, the zero-order almost vanishes on inspecting the photo. Taking λ₀ = 633 nm and L~8 mm, from Equation (1), Δn = 0.22 × 10⁻⁴. Appearently, even though the efficiency approaches to the ultimate, Δn is much less than the prediction of 10⁻⁴ [1]. In this case the temperature of the device rises to about 50˚C without cooling. But the diffraction is stable. However, if increasing the supersonic power furthermore, the diffraction will not be stable. In fact the power density on the transducer is about 6.8 W/cm² (3.4 W/[(π × 0.4²)cm²]) in this case. It is

comparable to the Bragg products, which transducer’s dimension is 5 × 0.8 cm² and is fed the power of 20 - 50 W. To lessen the heat, the interaction length L can be extended. This results in enlarging the dimensions of the device. Reversely, if cutting L for miniaturing the device, the heat must be more serious.

To test the feasibility of the portable device working as the Q-switch, exerting 8 kHz square wave, shown as Figure 5(a), to modulate the sound, the modulation of the zero-order diffraction with a He-Ne laser is monitored as Figure 5(b). The results show that the modulation of the light is synchronized to the one of the sound. The rise time is in the order of ~3 μs shown as Figure 5(c). This is comparable to the current Q-switch products.

4. Conclusions

The acousto-optic interaction length in R-N diffraction is first investigated by using the specially designed apparatus. The optimal interaction length and dimension of the transducer as well as the index difference for achieving the ultimate efficiency are realized. The portable device looked like solid configuration is designed based on the optimization. Taking advantage of the portable device the ultimate efficiency of 98% is achieved. Finally, the followings as the conclusion:

1) The optimal acousto-optic interaction length for achieving the ultimate efficiency relies essentially on the sound and almost not relates to the light.

2) To achieve the ultimate efficiency with the portable device the dimension of the transducer must match not only the frequency also the power of the sound.

3) Under the ultimate efficiency, the zero-order diffraction in dark field intimates the feasibility of R-N diffraction Q-switch.

Acknowledgements

This work is funded by the Science and Technology Program of Jiangsu, China (grant No. BE2014641), the Science and Technology Program of Jinlin, China (grant No. 2015SYHZ0009), the Projects of International Cooperation MOST (grant No. 2015DFR10230) and the Program of Jiangsu Key Laboratory of Medical Optics (grant No. Y332021203-4).

Cite this paper

Gu, H.D., Shao, Z.X., Yang, J., Zheng, C.Q. and Chen, R.T. (2017) Analysis and Optimum Design of a Portable Q-Switch Based on Raman-Nath Diffraction. Optics and Photonics Journal, 7, 20-25. https://doi.org/10.4236/opj.2017.78B004

References