Optics and Photonics Journal
Vol.07 No.08(2017), Article ID:78274,6 pages
10.4236/opj.2017.78B003
Combined Focusing and Flat-Field Spectrometer System for Extreme Ultraviolet Pulse
Yifan Kang1, Chao Wang2
1School of Science, Air Force Engineering University, Xi’an, China
2Key Laboratory of Ultra-Fast Photoelectric Diagnostics Technology, Xi’an Institute of Optics and Precision Mechanics, Chinese Academy of Sciences, Xi’an, China




Received: March 31, 2017; Accepted: August 7, 2017; Published: August 10, 2017
ABSTRACT
For reducing both extreme ultraviolet attosecond pulses energy loss in the focusing reflection process and measurement error caused by pulse focusing aberration, as well as improving the operability of pulse spectroscopy monitoring, a combined focusing and flat-field spectrometer analysis system for attosecond pulse is proposed and designed through step-by-step performance optimization. The focusing and spectrum-analyzing components are gold- coated grazing incidence to roidal mirror and grazing incidence concave focusing grating, respectively. The characteristic parameters of the system are given in details. The system proposed can find application in research platform of attosecond spectroscopy using high energy short attosecond pulse as basic probe tool.
Keywords:
Attosecond, High-Order Harmonics Generation, Flat-Field Spectrometer, Toroidal Mirror

1. Introduction
With the mature of carrier-envelop phase (CEP) stabilized few cycle laser technology, the strong field optics is now shifting from the stage of perturbative to extreme (or nonperturbative) nonlinear optical mechanism, of which one of the most exciting achievements is the establishment of new light source―single isolated attosecond laser pulse in extreme ultraviolet (XUV) or even X-ray electromagnetic spectrum based on strong field high-order harmonic generation (1 attosecond = 1as = 10−18 s) [1]. Since then, an attosecond research upsurge is overwhelmingly rising from physics, chemistry and materials science to even information processing and other fields [2]-[12]. So far, the world record of the shortest pulse is 67 as [10]. It is regarded as one of the mail goals in attosecond science to produce the even shorter pulse of sub-24 as with mJ energy per pulse in the future [1]. Undoubtedly, compared with that in visible or near infrared regionthe optics elements for propagating and analyzing these ultrashort pulses should be adjusted accordingly for its ultra-broad electromagnetic spectrum.
In this paper, we proposed a combined focusing and flat-field spectrum-ana- lyzing system based on a grazing incidence toroidal focusing mirror and toroidal concave grating. The toroidal instead of spherical mirror helps reduce the reflection energy loss and suppress the focusing aberrations. The simulated results related are given, together with the characteristic system parameters.
2. System Design
The proposed system is shown in Figure 1. Gas jet GJ-1 provides noble target atoms to generate XUV attosecond pulses through high-order harmonics generation process of CEP stabilized near-infrared few-cycle fem tosecond pulse, while GJ-2 supplies the gas atoms for attosecond diagnostics, such as attosecond transient absorption. Grazing incidence toriodal mirror (TM) [13] [14] [15] is used to focus the attosecond pulse from GJ-1 onto GJ-2, while the grazing incidence concave grating is to analyze the residual XUV spectrum [16] [17] [18]. The detailed structural parameters are established based on the specific operating requirements of TM and the grating.
The toriodal mirror used is gold-coated from ARW Optical Corporation, of which the two characteristic radiusas shown in Figure 2 are Rv = 90.5 mm and
Figure 1. Combined focusing and spectrometer system.

Figure 2. Description of toroidal mirror. (a) Front view; (b) 3D.
Rh = 3230 mm, with both radius tolerance smaller than ±1% and surface smooth accuracy better than l/2@632.8 nm. The focus characteristics of toroidal mirror can be decomposed into that in both meridian and sagittal planes, shown in Figure 3, and the corresponding mathematical descriptions are as follows [14].
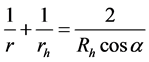 (1)
(1)
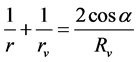 (2)
(2)
To eliminate the focus astigmatism, rh = rv must be met. Thus one can get the characteristic incidence angle of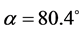 . The constraint relation in Equations (1) and (2) can then be reduced to the following one. In the optical system designed here, both the object point of GJ-1 and the image point of GJ-2 are set to be
. The constraint relation in Equations (1) and (2) can then be reduced to the following one. In the optical system designed here, both the object point of GJ-1 and the image point of GJ-2 are set to be 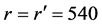 mm.
mm.
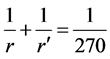 (3)
(3)
As for the grating, its curvature radius is Rg = 13,450 mm and the line density distribution in its concave surface is as following:
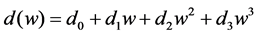 (4)
(4)
Here, d0 = 1200 l/mm refers to central grating linear density, w is the perpendicular distance from given grating line midpoint to the grating surface vertex normal, d1, d2, and d3arecontrol parameters,d1 = −3.546 mm−2, d2 = 8.656 ´ 10−3 mm−3, d3 = −2.209 ´ 10−5 mm−4. The grazing incidence flat-field grating spectrometer is shown in Figure 4, in which a = 87˚ refers to the characteristic incidence angle for best spectral dispersion, rg(λ) the distance from the grating surface center to the focus position of diffraction light of wavelength λ, and β(λ) the corresponding diffraction angle of the spectrum with the wavelength λ. rg is the perpendicular distance from the grating surface center to its spectral record plane.
Figure 3. Focusing properties of grazing incidencetoroidal mirror. (a) Meridional plane; (b) Sagittal plane.
For a grazing incidence concave grating, rg(l) and β(l) meet the following conditions:
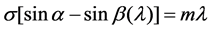 (5)
(5)
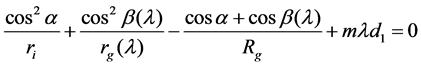 (6)
(6)
where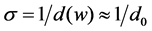 , m is the diffraction order and usually only m = 1 is taken for consideration. The dependence of both rg(λ) and β(λ) on wavelength is shown in Figure 5. rg = 563.2 mm can be achieved for l = 5 - 32 nm, indicating the best position of spectrum detector, such as CCD. Figure 6 gives the corresponding position on the spectral plane for the wavelength range mentioned.
, m is the diffraction order and usually only m = 1 is taken for consideration. The dependence of both rg(λ) and β(λ) on wavelength is shown in Figure 5. rg = 563.2 mm can be achieved for l = 5 - 32 nm, indicating the best position of spectrum detector, such as CCD. Figure 6 gives the corresponding position on the spectral plane for the wavelength range mentioned.
Figure 4. Grazing incidence concave grating spectrometer with flat-field imaging focusing.
Figure 5. Diffraction characteristics of concave grating.
Figure 6. Diffraction spectrum of 5 - 32 nm on focusing spectral plane.
3. Conclusion
This material presents a combined focusing and spectrum-analysis system for XUV attosecond pulse, in which the focusing and spectrum-analyzing components are gold-coated grazing incidence toroidal mirror and grazing incidence concave focusing grating, respectively. It possesses the feature of reducing both attosecond pulses energy loss in the focusing reflection process and measurement error caused by attosecond pulse focusing aberration measurement, as well as improving the operability of attosecond pulse spectroscopy monitoring. Through step-by-step performance optimization, the structure and characteristic parameters are given in details. The system proposed can find application in research platform of attosecond spectroscopy using high energy short attosecond pulse as basic probe tool. The simulated results are given, together with the characteristic system parameters.
Acknowledgements
Y. K. thanks the National Natural Science Foundation of China (Grant No. 11505289). C. W. thanks the National Natural Science Foundation of China (Grant No. 11675258) and the project support from Ministry of Personnel of Shaanxi Province.
Cite this paper
Kang, Y.F. and Wang, C. (2017) Combined Focusing and Flat-Field Spectrometer System for Extreme Ultraviolet Pulse. Optics and Photonics Jour- nal, 7, 14-19. https://doi.org/10.4236/opj.2017.78B003
References
- 1. Krausz, F. and Ivannov M. (2009) Attosecond Physics. Reviews of Modern Physics, 81, 163-234. https://doi.org/10.1103/RevModPhys.81.163
- 2. Calegari, F., Ayuso, D., Trabattoni, A., et al. (2014) Ultrafast Electron Dynamics in Phenylalanine Initiated by Attosecond Pulses. Science, 346, 336-339. https://doi.org/10.1126/science.1254061
- 3. Despre, V., Marciniak, A., Loriot, V., et al. (2015) Attosecond Hole Migra-tion in Benzene Molecules Surviving Nuclear Motion. The Journal of Physical Chemistry Letters, 6, 426-431. https://doi.org/10.1021/jz502493j
- 4. Li, R., Cheng, Y., Leng, Y., et al. (2016) Frontiers in Ultrafast Optics and Ul-tra-Intense Laser Technology. Scientia Sinica Informationis, 46, 1236-1254.
- 5. Salieres, P., Carre, B., Deroff, L.L., Grasbon, F., Paulus, G.G., Walther, H., Kopold, R., Becker, W., Milosevic, D.B., Sanpera, A. and Lewenstein, M. (2001) Feyn-man’s Path-Integral Approach for Intense-Laser-Atom Interactions. Science, 292, 902- 905. https://doi.org/10.1126/science.108836
- 6. Chang, Z.H. (2004) Single Attosecond Pulse and Xuvsupercontinuum in the High- Order Harmonic Plateau. Phys. Rev. A, 70, 043802/1-043802/8.
- 7. Agostine, P. and Dimauro, L.F. (2004) The Physics of Attosecond Light Pulses. Rep. Prog. Phys., 67, 813-855. https://doi.org/10.1088/0034-4885/67/6/R01
- 8. Sansone, G., Bendetti, E., Calegari, F., Vozzi, C., Avaldi, L., Filammini, R., Poletto, L., Villoresi, P., Altucci, C., Velotta, R., Stagira, S., De Silvestri, S. and Nisoli, M. (2006) Isolated Single-Cycle Atto-second Pulses. Science, 314, 443-446. https://doi.org/10.1126/science.1132838
- 9. Goulielmakis, E., Schultze, M., Hofstetter, M., Yakovlev, V.S., Gagnon, J., Uiberacher, M., Aquila, A.L., Gullikson, E.M., Attwood, D.T., Kienberger, R., Krausz, F. and Kleineber, U. (2008) Single-Cycle Nonlinear Optics. Science, 320, 1614-1617. https://doi.org/10.1126/science.1157846
- 10. Zhao, K., Zhang, Q., Chini, M., Wu, Y., Wang, X. and Chang, Z. (2012) Tai-loring a 67 Attosecond Pulse through Advantagous Phase-Mismatch. Opt. Lett., 37, 3891- 3893. https://doi.org/10.1364/OL.37.003891
- 11. Gouleilmakis, E., Yakovlev, V.S., Cavalieri, A.L., Uiberacker, M., Pervak, V., Apolonski, A., Kienberger, R., Kleineberg, U. and Krausz, F. (2007) Attosecond Control and Measurement: Lightwave Elec-tronics. Science, 317, 769. https://doi.org/10.1126/science.1142855
- 12. Feng, X.M., Gilbertson, S., Mashiko, H., Wang, H., Khan, S.D., Chini, M., Wu, Y., Zhao, K. and Chang, Z. (2009) Generation of Isolated Attosecond Pulses with 20 to 28 Femtosecond Lasers. Phys. Rev. Lett., 88, 173903. https://doi.org/10.1103/PhysRevLett.103.183901
- 13. Sakayanagi, Y. and Aoki, S. (1978) Soft x-Ray Imaging with To-roidal Mirrors. Appl. Opt., 17, 601-603. https://doi.org/10.1364/AO.17.000601
- 14. Garifo, L., Malvezzi, A.M. and Ton-dello, G. (1979) Grazing Incidence Spectrograph-Monochromator with a Focusing Toroidal Mirror. Appl. Opt., 18, 1900-1907. https://doi.org/10.1364/AO.18.001900
- 15. Tondello, G. (1979) The Use of a Toroidal Mirror as a Focusing Element for a Stigmatic Grazing Incidence Spectrometer. OpticaActa, 26, 357-371. https://doi.org/10.1080/713819999
- 16. Beutler, H.G. (1945) The Theory of the Concave Grating. J. Opt. Soc, Am., 35, 311- 350. https://doi.org/10.1364/JOSA.35.000311
- 17. Namioka, T. Theory of the Concave Grating. II. (1959) Applica-tion of the Theory to the Off-Plane EagleMounting in a Vacuum Spectrograph. J. Opt. Soc, Am., 49, 460- 465. https://doi.org/10.1364/JOSA.49.000460
- 18. Namioka, T. (1959) Theory of the Concave Grating. III. Seya-Namioka Monochromator. J. Opt. Soc, Am., 49, 951-961. https://doi.org/10.1364/JOSA.49.000951






