Int. J. Communications, Network and System Sciences, 2011, 4, 616-621
doi:10.4236/ijcns.2011.410074 Published Online October 2011 (http://www.SciRP.org/journal/ijcns)
Introduction to Secure PRNGs
Majid Babaei, Mohsen Farhadi
Department of C om put er Engineerin g, Shahrood University of Technology, Shahrood, Iran
Received July 8, 2011; revised August 15, 2011; accepted September 9, 2011
Abstract
Pseudo-Random Number Generators (PRNGs) are required for generating secret keys in cryptographic algo-
rithms, generating sequences of packet in Network simulations (workload generators) and other applications
in various fields. In this paper we will discuss a list of some requirements for generating a reliable random
sequence and then will present some PRNG methods which are based on combinational chaotic logistic map.
In the final section after a brief introduction to two statistical test packets, TestU01 and NIST suite tests, the
PRNG methods which are presented in the fourth section will be appraised under these test packets and the
results will be reported.
Keywords: Cryptography, Chaotic Random Bit Generator, NIST Test Suite, TestU01
1. Introduction
Pseudo-random number generators (PRNGs) are useful
in many applications such as the crypto-system in net-
work communication [1] also one of the important
methods in simulation is Mont Carlo [2] which needs to
generate very high quality pseudo-random sequence and
calculation of numerical integration which is not solved
by regular methods [3-5].
Regarding the threats to the security [3-16], the statisti-
cal quality of PRNGs is becoming more important than
before. For example a super computer might generate 109
random numbers per second and the cryptography algo-
rithm needs 1 016 random numbers to create a secure chan-
nel in a very important communications, thus small corre-
lation or other weaknesses in the generated sequence could
easily lead to the critical leak in several network layers.
The distributions should be prepared based on their
commercial applications such as “normal”, “exponen-
tial”, “poisson” and so on. But in this paper we consider
only the generation of uniformly distributed numbers. In
more details, we will focus on the real number sequence
which is uniformly distributed on the interval (0…1).
The basic point in generating pseudo-random number
is that these generators are deterministic because the
digital computers are not able to generate truly random
numbers. So the statistical test needs to be presented and
the PRNGs should pass a number of important statistical
tests, before being released for security usage in commu-
nication netwo rks.
In this paper, in Section 2, overview of using of cha-
otic maps as the reliable PRNG will be presented. Then
in Section 3 some requirements for generating a high
quality PRNG will be discussed . In Section 4 some class
of improving PRNGs will be presented and finally in
Section 5 two strong statistical test packages (i.e. NIST
suite tests and TestU01) will be introduced and all PRNG
methods which are tested by author, will be purposed
and the results will be reported into various tables.
2. Overview
Generation random numbers by combinational chaotic
maps is one of the best methods to improve statistical
properties. For example, in 2006, Wang et al. proposed a
pseudorandom number generator based on a z-logistic
map [4]. In 2007, Ergun and Ozogur proposed the novel
random bit sequence of a non-autonomous chaotic elec-
tronic circuit [5]. Then, Hu et a l. proposed a true random
number generator by computer mouse movement [6]. In
2009 Patidar et al. designed a rando m bit gener ato r based
on two chaotic logistic maps which is generated by
comparing the outputs of the both chaotic logistic maps
[7]. Recently in B. Fechner and A. Osterloh presented a
meta-level true random number generator [8].
3. Generating High Quality PRNG
In many papers there have been discussions about the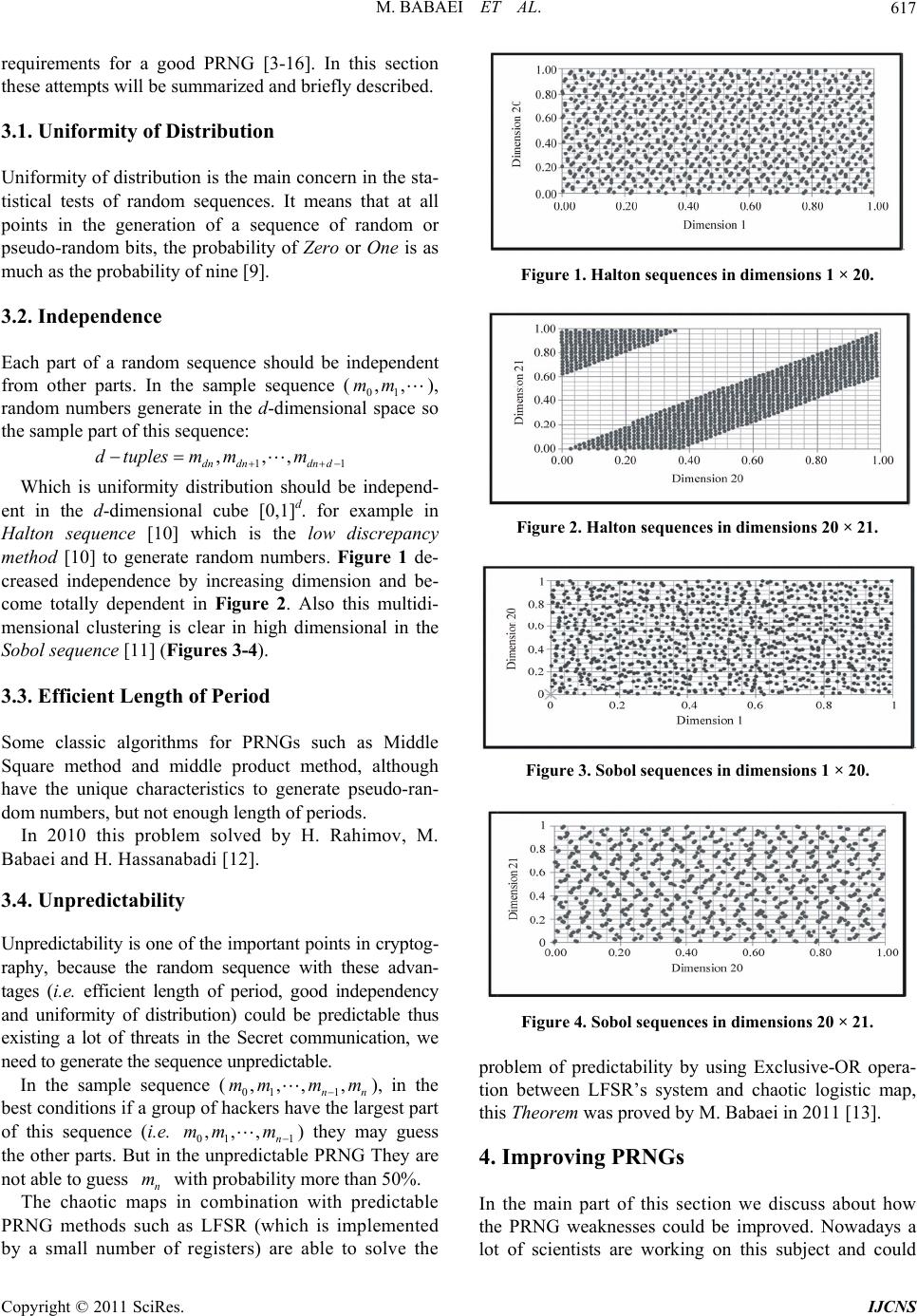

M. BABAEI ET AL.617

requirements for a good PRNG [3-16]. In this section
these attempts will be summarized and briefly described.
3.1. Uniformity of Distribution
Uniformity of distribution is the main concern in the sta-
tistical tests of random sequences. It means that at all
points in the generation of a sequence of random or
pseudo-random bits, the probability of Zero or One is as
much as the probability of nine [9].
3.2. Independence
Each part of a random sequence should be independent
from other parts. In the sample sequence (01 ),
random numbers generate in the d-dimensional space so
the sample part of this sequence:
,,mm
11
,,,
dndndn d
dtuplesmm m

 
Which is uniformity distribution should be independ-
ent in the d-dimensional cube [0,1]d. for example in
Halton sequence [10] which is the low discrepancy
method [10] to generate random numbers. Figure 1 de-
creased independence by increasing dimension and be-
come totally dependent in Figure 2. Also this multidi-
mensional clustering is clear in high dimensional in the
Sobol sequence [11] (Figures 3-4).
3.3. Efficient Length of Period
Some classic algorithms for PRNGs such as Middle
Square method and middle product method, although
have the unique characteristics to generate pseudo-ran-
dom numbers, but not enough length of periods.
In 2010 this problem solved by H. Rahimov, M.
Babaei and H. Hassanabadi [12].
3.4. Unpredictability
Unpredictability is one of the important points in cryptog-
raphy, because the random sequence with these advan-
tages (i.e. efficient length of period, good independency
and uniformity of distribution) could be predictable thus
existing a lot of threats in the Secret communication, we
need to generate the sequence unpredictable.
In the sample sequence (01 1n ), in the
best conditions if a group of hackers have the largest part
of this sequence (i.e. 01 1 ) they may guess
the other parts. But in the unpredictable PRNG They are
not able to guess with probability more than 50%.
,,,,
n
mmm m


,,,
n
m

mm
n
The chaotic maps in combination with predictable
PRNG methods such as LFSR (which is implemented
m
by a small number of registers) are able to solve the
Figure 1. Halton sequences in dimensions 1 × 20.
Figure 2. Halton sequences in dimensions 20 × 21.
Figure 3. Sobol sequences in dimensions 1 × 20.
Figure 4. Sobol sequences in dimensions 20 × 21.
problem of predictability by using Exclusive-OR opera-
tion between LFSR’s system and chaotic logistic map,
this Theorem was proved by M. Babaei in 2011 [13].
4. Improving PRNGs
In the main part of this section we discuss about how
the PRNG weaknesses could be improved. Nowadays a
lot of scientists are working on this subject and could

M. BABAEI ET AL. 618
prepare reliable methods to improve these defects in
generators, especially the applications of PRNGs in
cryptography need to be more efficient than other appli-
cations.
4.1. Decimation Method
In this method two PRNGs generate random numbers in
two different sequences, (the type of PRNGs may be the
same or different). Combination based on this method is
able to generate more efficient random sequence.
Based on this method if a PRNG generated a sequence
such as:
12
,,,
n
pp p
By using of Decimation method generated a sequence
like this:
12
,,,
m
qq q
By defining that:
j
jk
qp where chose as a constant efficient
value. 1k
Decimation algorithm is described below:
1) float* Decimation()
2) {
3) float *finalSeq;
4) boolean continueGenerating = True;
5) int count PRNG = 0;
6) char ans;
7) finalSeq = new float [100];
8) while (Continue Generating);
9) {
10) int loop Length = PRNG1();
11) for(int i=1; I loopLength; i++);

12) flooat random Number = PRNG2();
13) finalSeq [countPRNG] = random Number;
14) }
15) cout “Do you want more? (y/n)” endl;  
16) cin ans; 
17) if (ans == ‘n’ || ans ==‘N’);
18) break;
19) }
20) return finalSeq;
21) }
In other words this algorith m in Line 10 generates se-
quence () and in Line 12 generates se-
quence (123 ), so Decimation method gener-
ates the final sequence as below:
123
,,,,
n
ppp p
,,,,
m
qqq q
112123 12
, ,,...,n
p
pp pppppp
qq qq
 
Many papers proved that generating random sequence
by this method is more efficient than discrete sequences
[19], meaning that:
Distribution (SeqDecimation) > distribution (PRNG1)
and
Distribution (SeqDecimation) > distribution (PRNG2).
4.2. XOR Operation and Combination PRNGs
One of the popular models to improve PRNG’s defects is
combining k numbers of generator by Xor operation. For
example, if each of the generators is defined by a primi-
tive trinomial such as:
() 1
rk sk
k
PT xxx

.
This is the main structure of Fibonacci LFSR genera-
tors which is distinct primitive degrees, then proved
that the combination of these k generators has a
rk
period of at least.
1
1
2(2
krk
k
 


1)
In this case, we present various PRNGs with different
efficiencies, which can be classified into three main
groups.
 Class 1: Classic Generator XOR Classic Generator
 Class 2: Classic Generator XOR Modern Generator
 Class 3: Modern Generator XOR Modern Generator
Based on the classification classic generators (e.g.
Low discrepancy methods [10], High discrepancy meth-
ods [10], LFSR methods [13] and …) and modern gen-
erators contain any type of discrete chaotic maps (e.g.
Henon map [14], Logistic map [14], Gauss map [14] …).
4.3. Shuffling Method
In this method two PRNGs generate two different ran-
dom sequences like the Decimation method, one of the
sequences stores in the buffer area and the other chooses
from buffer side.
Suppose that, there are two PRNGs such as:
01
:(,,...,)
n
Ppp p
where P is a PRNG’s function.
01
:(, ,...,)
m
Qqq q
where Q is a PRNG’s function, and m < n.
By using of buffer B (minimum size n), storing se-
quence P in the buffer B then, by using of sequence Q
chooses, m values of buffer B and put them in the final
result sequence.
Shuffling algorithm is described below:
1) float *Shuffling()
2) {
3) float *finalSeq;
4) float *buffer;
5) int bufferLength = 100;
6) char ans;
7) boolean continueGenerating = True;
8) int countPRNG = 0;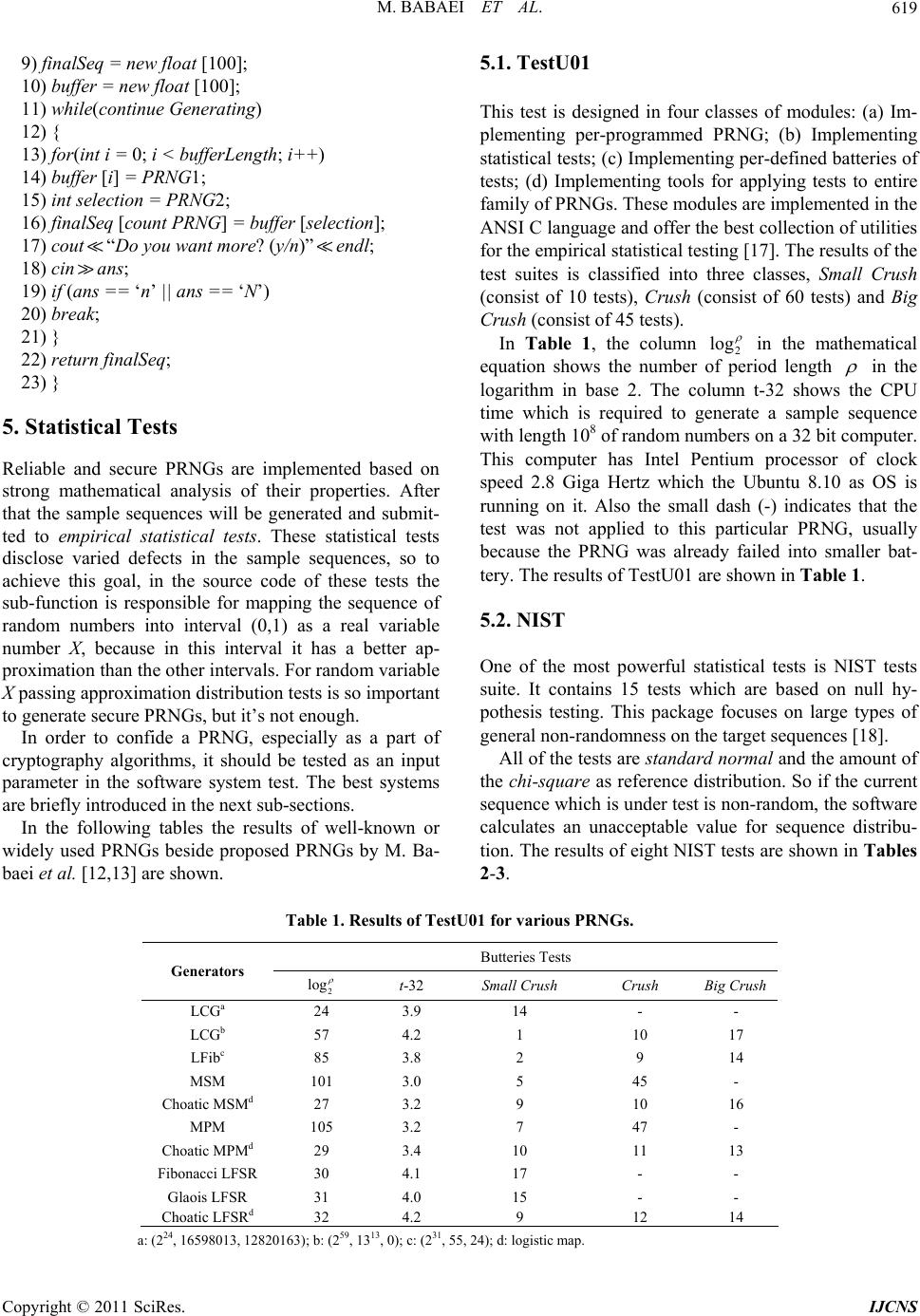

M. BABAEI ET AL. 619
5.1. TestU01
9) finalSeq = new float [100];
10) buffer = new float [100];
11) while(continue Generating) This test is designed in four classes of modules: (a) Im-
plementing per-programmed PRNG; (b) Implementing
statistical tests; (c) Implementing per-defined batteries of
tests; (d) Implementing tools for applying tests to entire
family of PRNGs. These modules are implemented in th e
ANSI C language and offer the best collection of utilities
for the empirical statistical testing [17]. The results of the
test suites is classified into three classes, Small Crush
(consist of 10 tests), Crush (consist of 60 tests) and Big
Crush (consist of 45 tests).
12) {
13) for(int i = 0; i < bufferLength; i++)
14) buffer [i] = PRNG1;
15) int selection = PRNG2;
16) finalSeq [count PRNG] = buffer [selection];
17) cout“Do you want more? (y/n)” endl;  
18) cinans; 
19) if (ans == ‘n’ || ans == ‘N’)
20) break;
21) } In Table 1, the column 2
log

in the mathematical
equation shows the number of period length

in the
logarithm in base 2. The column t-32 shows the CPU
time which is required to generate a sample sequence
with length 108 of random numbers on a 32 bit computer.
This computer has Intel Pentium processor of clock
speed 2.8 Giga Hertz which the Ubuntu 8.10 as OS is
running on it. Also the small dash (-) indicates that the
test was not applied to this particular PRNG, usually
because the PRNG was already failed into smaller bat-
tery. The results of TestU01 are shown in Table 1.
22) return finalSeq;
23) }
5. Statistical Tests
Reliable and secure PRNGs are implemented based on
strong mathematical analysis of their properties. After
that the sample sequences will be generated and submit-
ted to empirical statistical tests. These statistical tests
disclose varied defects in the sample sequences, so to
achieve this goal, in the source code of these tests the
sub-function is responsible for mapping the sequence of
random numbers into interval (0,1) as a real variable
number X, because in this interval it has a better ap-
proximation than the other intervals. For random variable
X passing approximation distribution tests is so important
to generate secure PRNGs, but it’s not enough.
5.2. NIST
One of the most powerful statistical tests is NIST tests
suite. It contains 15 tests which are based on null hy-
pothesis testing. This package focuses on large types of
general non-randomness on the target sequences [18].
In order to confide a PRNG, especially as a part of
cryptography algorithms, it should be tested as an input
parameter in the software system test. The best systems
are briefly introduced in the next sub-sections.
All of the tests are standard norma l and the amount of
the chi-square as reference distribution. So if the current
sequence which is under test is non-random, the software
calculates an unacceptable value for sequence distribu-
tion. The results of eight NIST tests are shown in Tables
2-3.
In the following tables the results of well-known or
widely used PRNGs beside proposed PRNGs by M. Ba-
baei et al. [12,13] are shown.
Table 1. Results of TestU01 for various PRNGs.
Butteries Tests
Generators
2
log

t-32 Small Crush Crush Big Crush
LCGa 24 3.9 14 - -
LCGb 57 4.2 1 10 17
LFibc 85 3.8 2 9 14
MSM 101 3.0 5 45 -
Choatic MSMd 27 3.2 9 10 16
MPM 105 3.2 7 47 -
Choatic MPMd 29 3.4 10 11 13
Fibonacci LFSR 30 4.1 17 - -
Glaois LFSR 31 4.0 15 - -
Choatic LFSRd 32 4.2 9 12 14
a: (224, 16598013, 12820163); b: (259, 1313, 0); c: (231, 55, 24); d: logistic map.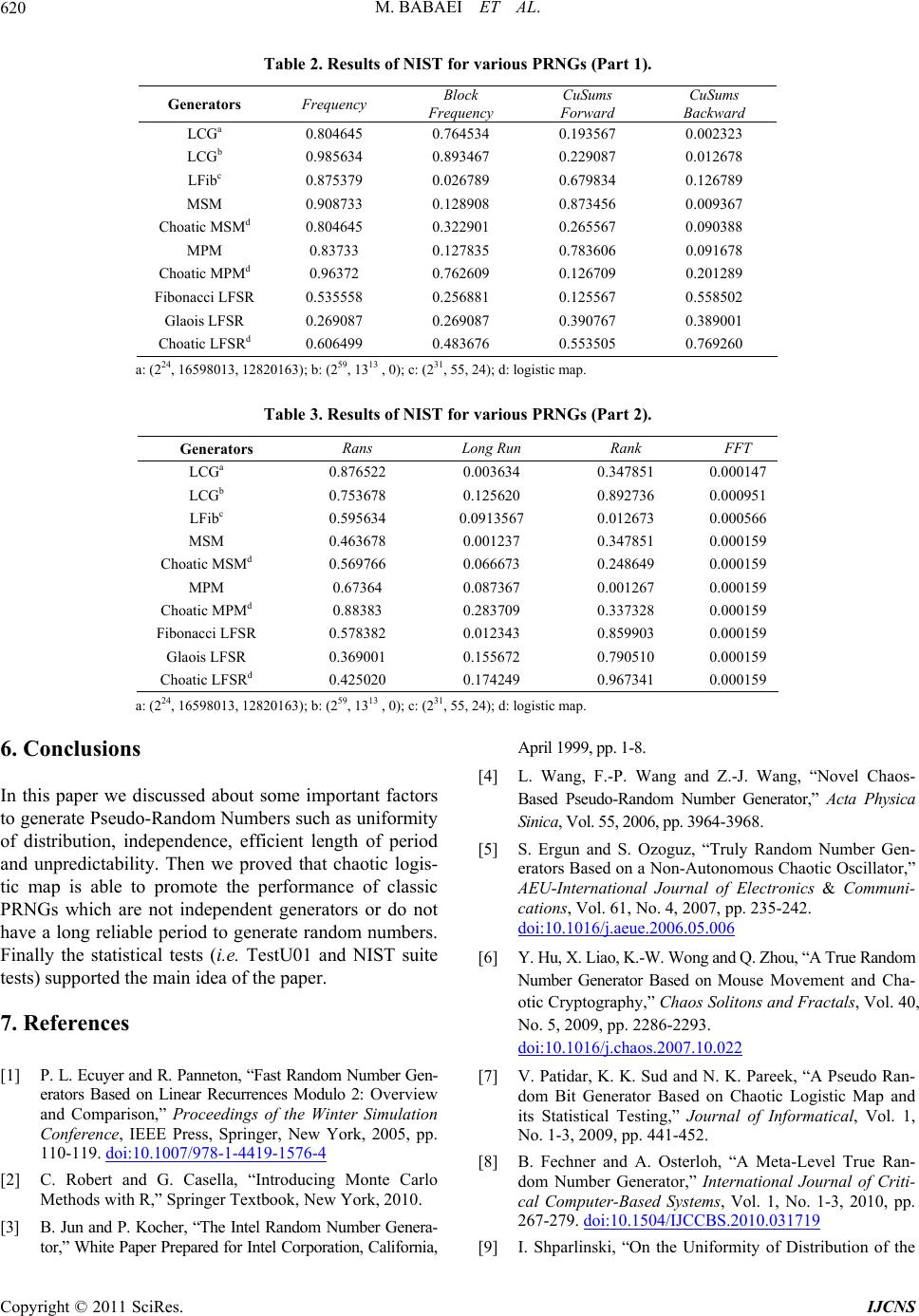

M. BABAEI ET AL. 620
Table 2. Results of NIST for various PRNGs (Part 1).
Generators Frequency Block
Frequency CuSums Forward CuSums Backward
LCGa 0.804645 0.764534 0.193567 0.002323
LCGb 0.985634 0.893467 0.229087 0.012678
LFibc 0.875379 0.026789 0.679834 0.126789
MSM 0.908733 0.128908 0.873456 0.009367
Choatic MSMd 0.804645 0.322901 0.265567 0.090388
MPM 0.83733 0.127835 0.783606 0.091678
Choatic MPMd 0.96372 0.762609 0.126709 0.201289
Fibonacci LFSR 0.535558 0.256881 0.125567 0.558502
Glaois LFSR 0.269087 0.269087 0.390767 0.389001
Choatic LFSRd 0.606499 0.483676 0.553505 0.769260
a: (224, 16598013, 12820163); b: (259, 1313 , 0); c: (231, 55, 24); d: l o gistic m ap.
Table 3. Results of NIST for various PRNGs (Part 2).
Generators Rans Long Run Rank FFT
LCGa 0.876522 0.003634 0.347851 0.000147
LCGb 0.753678 0.125620 0.892736 0.000951
LFibc 0.595634 0.0913567 0.012673 0.000566
MSM 0.463678 0.001237 0.347851 0.000159
Choatic MSMd 0.569766 0.066673 0.248649 0.000159
MPM 0.67364 0.087367 0.001267 0.000159
Choatic MPMd 0.88383 0.283709 0.337328 0.000159
Fibonacci LFSR 0.578382 0.012343 0.859903 0.000159
Glaois LFSR 0.369001 0.155672 0.790510 0.000159
Choatic LFSRd 0.425020 0.174249 0.967341 0.000159
a: (224, 16598013, 12820163); b: (259, 1313 , 0); c: (231, 55, 24); d: l o gistic m ap.
6. Conclusions
In this paper we discussed about some important factors
to generate Pseudo-Random Numbers such as uniformity
of distribution, independence, efficient length of period
and unpredictability. Then we proved that chaotic logis-
tic map is able to promote the performance of classic
PRNGs which are not independent generators or do not
have a long reliable period to generate random numbers.
Finally the statistical tests (i.e. TestU01 and NIST suite
tests) supported the main idea of the paper.
7. References
[1] P. L. Ecuyer and R. Panneton, “Fast Random Number Gen-
erators Based on Linear Recurrences Modulo 2: Overview
and Comparison,” Proceedings of the Winter Simulation
Conference, IEEE Press, Springer, New York, 2005, pp.
110-119. doi:10.1007/978-1-4419-1576-4
[2] C. Robert and G. Casella, “Introducing Monte Carlo
Methods with R,” Springer Textbook, New York, 2010.
[3] B. Jun and P. Kocher, “The Intel Random Number Genera-
tor,” White Paper Prepared for Intel Corporation, California,
April 1999, pp. 1-8.
[4] L. Wang, F.-P. Wang and Z.-J. Wang, “Novel Chaos-
Based Pseudo-Random Number Generator,” Acta Physica
Sinica, Vo l. 55, 2 006, pp. 3 964-3968.
[5] S. Ergun and S. Ozoguz, “Truly Random Number Gen-
erators Based on a Non-Autonomous Chaotic Oscillator,”
AEU-International Journal of Electronics & Communi-
cations, Vol. 61, No. 4, 2007, pp. 235-242.
doi:10.1016/j.aeue.2006.05.006
[6] Y. Hu, X. Liao , K.-W . Won g and Q. Zhou , “A True Ra ndom
Number Generator Based on Mouse Movement and Cha-
otic Cryptography,” Chaos Solitons and Fractals, Vol. 40,
No. 5, 2009, pp. 2286-2293.
doi:10.1016/j.chaos.2007.10.022
[7] V. Patidar, K. K. Sud and N. K. Pareek, “A Pseudo Ran-
dom Bit Generator Based on Chaotic Logistic Map and
its Statistical Testing,” Journal of Informatical, Vol. 1,
No. 1-3, 2009, pp. 441-452.
[8] B. Fechner and A. Osterloh, “A Meta-Level True Ran-
dom Number Generator,” International Journal of Criti-
cal Computer-Based Systems, Vol. 1, No. 1-3, 2010, pp.
267-279. doi:10.1504/IJCCBS.2010.031719
[9] I. Shparlinski, “On the Uniformity of Distribution of the

M. BABAEI ET AL.621
Decryption Exponent in Fixed Encryption Exponent RSA,”
Journal of Computation Theory and Ma t he m at i cs , Vol. 92,
No. 3, 2004, pp.143-147.
[10] X. Wang and F. J. Hickernell, “Randomized Halton Se-
quences,” Journal of Mathematical and Computer Mod-
elling, Vol. 32, 2000, p. 2000.
[11] P. S. Kumar, R. Subramanian and D. T. Selvam, “Ensur-
ing Data Storage Security in Cloud Computing Using
Sobol Sequence,” 1st International Conference on Par-
allel, Distributed and Grid Computing, 2010, pp. 217-
222.
[12] H. Rahimov, M. Babaei and H. Hassanabadi, “Improving
Middle Square Method RNG Using Chaotic Map,” Jour-
nal of Applied Mathematics, Vol. 2, No. 4, 2010, pp.
482-486.
[13] M. Babaei and M. Ramyar, “Improved Performance of
LFSR’s System with Discrete Chaotic Iterations,” World
Applied Science Journal, Vol. 13, No. 7, 2011, pp. 1720-
1725.
[14] A. J. Menezes, P. C. van Oorschot and S. A. Vanstone,
“Handbook of Applied Cryptography,” CRC Press, New
York, 1997.
[15] B. Fechner and A. Osterloh, “A Meta-Level True Ran-
dom Number Generator,” International Journal of Criti-
cal Computer-Based Systems, Vol. 1, No. 1-3, 2010, pp.
267-279. doi:10.1504/IJCCBS.2010.031719
[16] B. D. McCullough, “A Review of TESTU01,” Journal of
Applied Econometrics, Vol. 21, No. 5, 2006, pp. 677-682.
doi:10.1002/jae.917
[17] NIST Special Publication 800-22, “A Statistical Test
Suite for Random and Pseudorandom Number Generators
for Cryptographic Applications,” Octob er 2000.
[18] M. L. Uscher, “A Portable High-Quality Random Number
Generator for Lattice Field Theory Simu-Lations,” Computer
Physics Communications, Vol. 79, 1994, p p. 100 -110.