J. Software Engineering & Applications, 2009, 2: 137-143
doi:10.4236/jsea.2009.23020 Published Online October 2009 (http://www.SciRP.org/journal/jsea)
137
Cyclomatic Complexity and Lines of Code: Empirical
Evidence of a Stable Linear Relationship
Graylin JAY1, Joanne E. HALE2, Randy K. SMITH1, David HALE2, Nicholas A. KRAFT1,
Charles WARD1
1Department of Computer Science, University of Alabama, Tuscaloosa, USA; 2 Department of Management Information Systems,
University of Alabama, Tuscaloosa, USA.
Received April 21st, 2009; revised June 9th, 2009; accepted June 12nd, 2009.
ABSTRACT
Researchers have often commented on the high correlation between McCabe’s Cyclomatic Complexity (CC) and lines
of code (LOC). Many have believed this correlation high enough to justify adjusting CC by LOC or even substituting
LOC for CC. However, from an empirical standpoint the relationship of CC to LOC is still an open one. We undertake
the largest statistical study of this relationship to date. Employing modern regression techniques, we find the linearity
of this relationship has been severely underestimated, so much so that CC can be said to have absolutely no explana-
tory power of its own. This research presents evidence that LOC and CC have a stable practically perfect linear rela-
tionship that holds across programmers, languages, code paradigms (procedural versus object-oriented), and software
processes. Linear models are developed relating LOC and CC. These models are verified against over 1.2 million
randomly selected source files fro m the SourceFo rge co de repository. These files repr esent softwa re projects from three
target languages (C, C++, and Java) and a variety of programmer experience levels, software architectures, and de-
velopment methodologies. The models developed are found to successfully predict roughly 90% of CC’s variance by
LOC alone. This suggest not only that the linear relationship between LOC and CC is stable, but the aspects of code
complexity that CC measures, such as the size of the test case space, grow linearly with source code size across lan-
guages and programming paradigms.
Keywords: Software Complexity, Software Metrics, Cyclo matic Complexity
1. Introduction
Software complexity is traditionally a direct indicator of
software quality and cost [1-6]. The greater the com-
plexity (by some measure) the more fault prone the soft-
ware resulting in higher cost. Much effort has gone into
identifying techn iques and metrics to ‘measure’ the com-
plexity of software and software modules [7]. Logically,
many of these measures have been shown to be corre-
lated in some manner. Understanding these relationships
is important to understanding and evaluating the metrics
themselves and ultimately in reducing software devel-
opment and maintenance efforts. This research reexam-
ines the relationship between Lines of Code (LOC) and
McCabe’s Cyclomatic Complexity (CC) a traditional
complexity metric.
First introduced in 1976 [8], McCabe’s Cyclomatic
Complexity (CC) is intended to measure software com-
plexity by examining the software program’s flow graph.
In practice, CC amounts to a count of the “decision
points” present in the software. CC can be calculated as:
CC = E – N + 2P
where
E is the number of edges,
N is the number of nodes, and
P is the number of discrete connected components.
CC was originally meant as a measure of the size of
the test case space [8].
While numerous studies [1–3,9] have examine the re-
lationship between LOC and CC, few have made it their
central point of inquiry. As a result, while many state,
sometimes strongly, that LOC and CC have a linear rela-
tionship, few investigate statistical issues such as the
distribution of variance among LOC and CC. Shepperd,
for example, uses data from previous studies to argues
that CC was often “merely a proxy for ... lines of code”
[9]. Many investigators either consciously or serendipi-
tously avoid the issue entirely by using mixed metrics

Cycloma t ic Complexity and Lines of Code: Empirical Evidence of a Stable Linear Relationship 138
such as error density or adjustments for size [5, 10]. Oth-
ers investigating the relationship of CC to some other
factor explicitly tested for a detrimental multi-collinear
effect from LOC [11]. While previous studies have indi-
cated the large role that LOC seems to play in CC [12],
they stop short of claiming a general model of the rela-
tionship. While we do not seek to settle th e issue, it is for
these reasons that this research reexamines the relation-
ship of LOC and CC in the context of a large empirical
study.
2. Study Methodology
As a baseline and to confirm the LOC/CC relationship
results reported in the literature, a pilot study look ed at 5
NASA projects from the PROMISE Software Engineer-
ing Repository [13]. The PROMISE Repository is a col-
lection of publicly available datasets for software engi-
neering researchers. The NASA projects were originally
archived in the NASA Metrics Data Program. Table 1
shows the Pearson Moment of Correlation between LOC
and CC.
The correlation is remarkably high (average 0.896),
yet does have a significant variance. When expanding on
this pilot, variance was examined closely for the larger
sample population.
2.1 Sample Population
For the larger study, the SourceForge.net (SourceForge)
software repository was chosen because of its breadth
and popularity [14]. SourceForge is the most popular
public software repository on the Internet and is second
only to Download.com as the most popular provider of
software on the web [15]. SourceForge is home to pro-
jects actively sponsored and developed by companies
such as HP [16] and IBM [17] as well as academic and
other open-source projects. SourceForge is home to over
170 thousand different software projects all with their
full codebases publicly available.
2.2 Population Candidate Stratification
Based on the observations of the PROMISE Repository,
the large sample population of SourceForge projects was
stratified based on three popular languages: C, C++ and
Java. Identification of the implementation language is
part of project creation on SourceForge. This self-re-
ported information was used to establish three subject
candidate populations. Table 2 shows the number, by
language, of candidate projects considered for this study
as well as the number of projects actually selected and
analyzed.
Projects that mixed candidate languages were elimi-
nated. That is: while a project that employed Python and
C was considered an acceptable candidate, a project that
used Java and C++ was not.
2.3 Subject Selection
One thousand subjects were randomly chosen from the
stratified lists (column two of table 2). All of the chosen
subjects needed to employ the Subversion (SVN) version
control system [18] rather than the more traditional CVS,
so this criterion was used to further discriminate amongst
projects. The speed and reliability of SVN made this ex-
periment practical. The choice of SVN over CVS did not
affect the sample statistics. A complete discussion of this
issue and other analysis is given in the Results section.
Table 1. Representative NASA projects and their pearson moment between LOC and CC
Project Language Pearson Moment
spacecraft instrument C 0.94
real-time predictive simulation C 0.82
data storage manager C++ 0.90
science data processor C++ 0.96
satellite flight software C 0.86
Table 2. Candidate population sizes (in projects) and final number of active subject s
Language Candidate Projects Selected Active Projects (at least one source file)
Java 21,739 728
C 13,336 749
C++ 15,194 747

C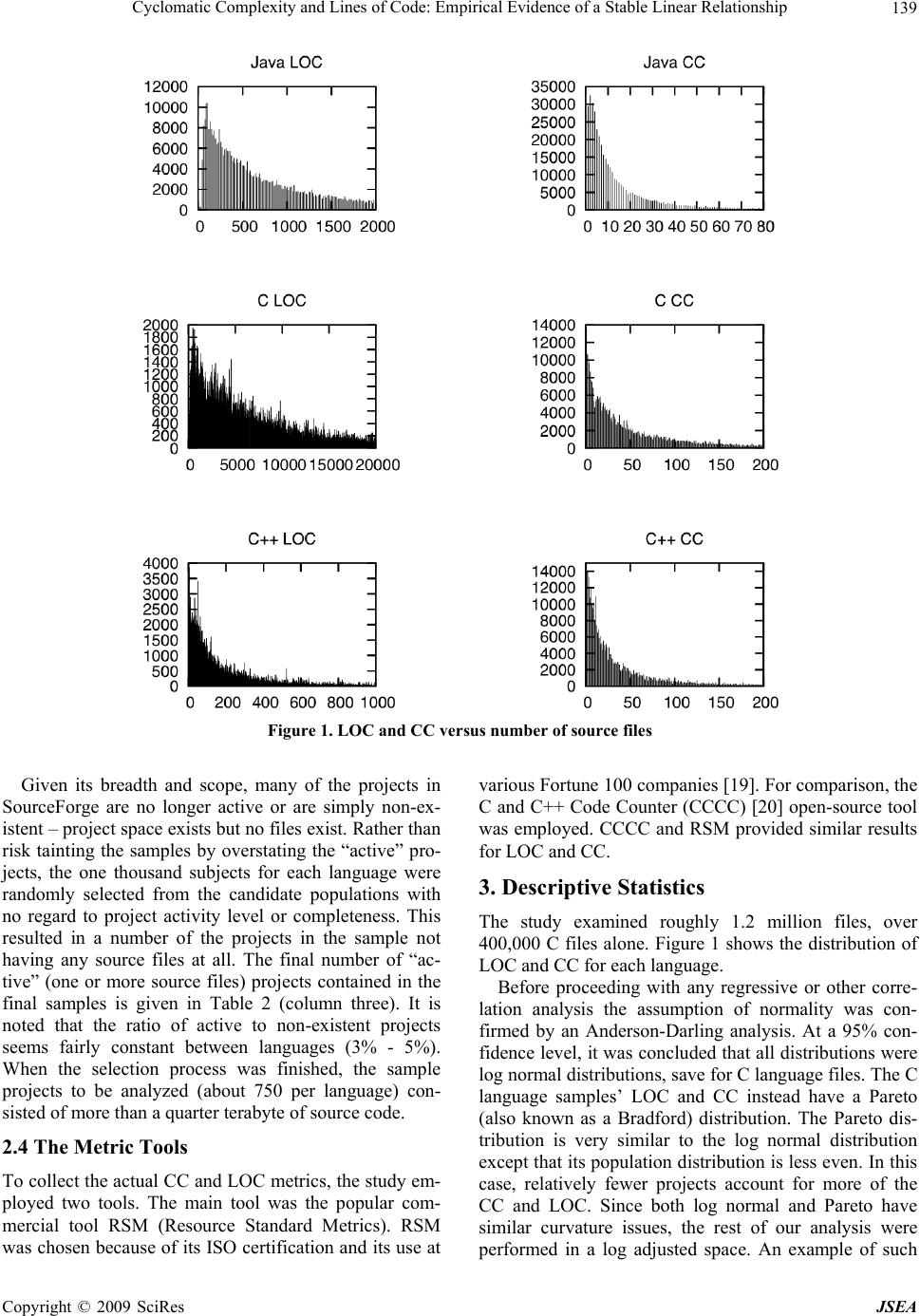ycloma t ic Complexity and Lines of Code: Empirical Evidence of a Stable Linear Relationship139
Figure 1. LOC and CC versus number of source files
Given its breadth and scope, many of the projects in
SourceForge are no longer active or are simply non-ex-
istent – project space exists but no files exist. Rather than
risk tainting the samples by overstating the “active” pro-
jects, the one thousand subjects for each language were
randomly selected from the candidate populations with
no regard to project activity level or completeness. This
resulted in a number of the projects in the sample not
having any source files at all. The final number of “ac-
tive” (one or more source files) projects contained in the
final samples is given in Table 2 (column three). It is
noted that the ratio of active to non-existent projects
seems fairly constant between languages (3% - 5%).
When the selection process was finished, the sample
projects to be analyzed (about 750 per language) con-
sisted of more than a quarter terabyte of source code.
2.4 The Metric Tools
To collect the actual CC and LOC metrics, the study em-
ployed two tools. The main tool was the popular com-
mercial tool RSM (Resource Standard Metrics). RSM
was chosen because of its ISO certification and its use at
various Fortune 100 companies [19]. For comparison, the
C and C++ Code Counter (CCCC) [20] open-source tool
was employed. CCCC and RSM provided similar results
for LOC and CC.
3. Descriptive Statistics
The study examined roughly 1.2 million files, over
400,000 C files alone. Figure 1 shows the distribution of
LOC and CC for each language.
Before proceeding with any regressive or other corre-
lation analysis the assumption of normality was con-
firmed by an Anderson-Darling analysis. At a 95% con-
fidence level, it was concluded that all distributions were
log normal distributions, save for C language files. The C
language samples’ LOC and CC instead have a Pareto
(also known as a Bradford) distribution. The Pareto dis-
tribution is very similar to the log normal distribution
except that its population distributio n is less even. In this
case, relatively fewer projects account for more of the
CC and LOC. Since both log normal and Pareto have
similar curvature issues, the rest of our analysis were
performed in a log adjusted space. An example of such

Cycloma t ic Complexity and Lines of Code: Empirical Evidence of a Stable Linear Relationship 140
an adjustment is presented below in Figure 2, which
shows the log adjusted LOC distribution for the C++
samples. These adjustments result in almost ideal normal
curves for the sample populations.
3.1 Variance Issues
To test the assumption of ev enly distributed variances, A
Breusch-Pagan [21] test was performed on each of the
samples with a significance level of .05. In each case
homoscedasticity was rejected. This indicates that the
variance within the sample populations was not uniform.
This is a significant finding. Equality of variance is a
required assumptio n for most traditional forms of regres-
sion. These traditiona l forms of regression are exactly the
types of regression used in previous research. Our results
indicate that this unevenness is more than just a theoreti-
cal concern. Below it is shown that a Pearson analysis is
skewed compared to a more robust analysis.
4. Results
The Pearson Moment was calculated between the log of
the LOC and the log of the CC for the samples as was the
explanatory power of the log of the LOC over the vari-
ance of the log of the CC. These log transformations ad-
just for the curvature present in the samples' log normal
distributions. Table 3 gives the Pearson Moment and
variance by langu age and tool. The CCCC tool cou ld not
process Java files.
Earlier, it was discussed that samples were limited to
those that utilized SVN. As a check that this did not in-
validate the results, a small random sample of 32 projects
per language were selected that utilized another open-
source versioning system (CVS). Table 4 gives those
results.
Table 3 and Table 4 below indicate a strong linear cor-
relation between the log of LOC and the log of CC, and
hence between LOC and CC. This correlation is strong
regardless of language. When CCCC failed to be capable
of processing a source file in a project, the project was
removed from the CCCC sample. Despite the fact that this
meant CCCC's sample was differentiated, the two tools
still both indi cate the sam e strong correla ti on.
Figure 2. Log adjusted C++ LOC distribution
Table 3. Pearson moment in log adjusted space by language and tool
Language Tool Files Pearson Moment Percent of Variance
Java RSM
CCCC 480,336 NA 0.88 NA 78.3 NA
RSM 401,474 0.88 78.4
C CCCC 399,483 0.91 82.7
RSM 411,718 0.87 76.2
C++ CCCC 410,051 0.85 72.9

Cycloma t ic Complexity and Lines of Code: Empirical Evidence of a Stable Linear Relationship141
Table 4. Pearson moment in log adjusted space by language (32 CVS projects each)
Language Pearson Moment Percent of Variance
Java 0.91 82.5
C 0.87 76.8
C++ 0.93 86.4
Table 5. Coefficient of determination for Siegal repeated median regression and “equivalent” pearson moment
Language Coefficient of Determination Equivalent Pearson Moment
Java 0.87 0.93
C 0.93 0.97
C++ 0.97 0.98
Concerns over variance made it necessary to run a
more robust test than Pearson. The test chosen was the
Siegal repeated median regression, a technique known to
be robust against heteroscedasticity and tolerant to up to
50% of the data points being outliers [22]. Siegal is
computationally intensive. To accommodate the compu-
tational complexity given the sample size, 3000 data
points were randomly sub-selected from the samples. A
linear model for a each sub-sample was created using
repeated median regression. These models were then
used to predict CC for all the samples of a language
population based solely on LOC. To assess how predic-
tive these models were, their coefficient of determination
were computed (see column two of Table 5.). So that
the accuracy of our repeated median regression models
could be compared to more traditional models, the
equivalent Pearson Moment for each coefficient were
also calculated. These are what the Pearson Moments in
a traditional model would have to have been in order to
account for the same amount of variance as our Sie-
gal-based models. All of the calculations here described
were performed in the same log adjusted space as with
our previous Pearson Moment calculations. The results
for each language ar e shown in Table 5.
As shown in Table 5, once the study accounted for
issues of variance LOC and CC, extremely accurate
linear models were developed. It is worth reiterating:
while the models were developed using sub-samples,
the va lues in Tab le 5 are from ap pl ying the mod el to the
whole populations. Our models can use log of LOC to
explain all but 13% of the log of CC's variance (on av-
erage they explain 90% of the variance). Based on these
results we propose:
LOC and CC are measuring the same property.
Whether this means that LOC and CC are merely esti-
mates of each other or if they are both estimates of some
third factor is left as an open question. Regardless, the
fact that LOC and CC do measure each other indicates
that models using one or the other must be careful of
collinear effects.
Figure 3 shows how similar the models are for each
language. Figure 3 shows the graph of the Siegal re-
peated median model for each language. For clarity's
sake this graph is in the un-adjusted space.
4.1 Model Validation
It is worth reiterating how our Siegal repeated median
models were developed. They were built using data fro m
a small portion of each language population and then
used to predict attributes of the entire, larger, language
population. This is an important point because it means
that the link between LOC and CC that the models rep-
resent have been externally validated as indicated by
Zuse [23]. We have used LOC to accurately predict CC
in a large (hundred of projects, thousand s of files) varied
(professional, amateur, and academic) population.
SourceForge provides a heterogeneous cross-section of
the general software population.
5. Threats to Validity
It would be misleading to think that this study concerning
metric directly mitigates internal validity threats. While
they are considered metrics in their own right, there is a
great deal of dispute as to how to practically “measure”
CC and LOC. We attempt to address this issue through
our use of multiple measures in the form of our two
toolsets. However, this is by no means an exhaustive
solution to the problem and was not possible for Java.
We present strong statistical evidence for the general
applicability of our findings across lan guages, paradigms,
and skill-sets. We stress that while this generally appli-
cability is statistically true, it is only true in aggregate.
The general applicability to any given project is still an
pen issue. o

C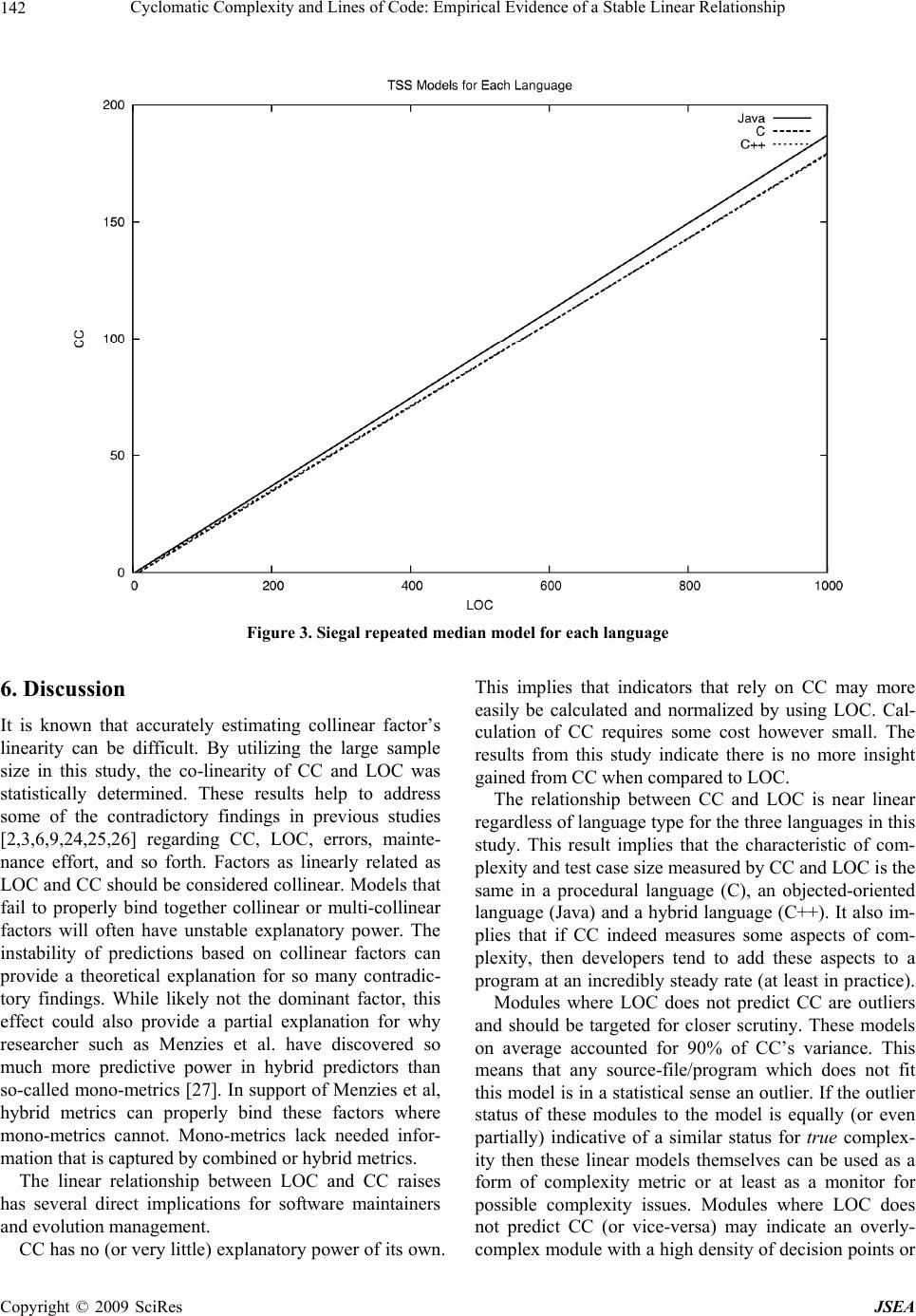ycloma t ic Complexity and Lines of Code: Empirical Evidence of a Stable Linear Relationship 142
Figure 3. Siegal repeated median model for each language
6. Discussion
It is known that accurately estimating collinear factor’s
linearity can be difficult. By utilizing the large sample
size in this study, the co-linearity of CC and LOC was
statistically determined. These results help to address
some of the contradictory findings in previous studies
[2,3,6,9,24,25,26] regarding CC, LOC, errors, mainte-
nance effort, and so forth. Factors as linearly related as
LOC and CC should be consid ered collinear. Models that
fail to properly bind together collinear or multi-collinear
factors will often have unstable explanatory power. The
instability of predictions based on collinear factors can
provide a theoretical explanation for so many contradic-
tory findings. While likely not the dominant factor, this
effect could also provide a partial explanation for why
researcher such as Menzies et al. have discovered so
much more predictive power in hybrid predictors than
so-called mono-metrics [27]. In support of Menzies et al,
hybrid metrics can properly bind these factors where
mono-metrics cannot. Mono-metrics lack needed infor-
mation that is captured by combined or hybrid metrics.
The linear relationship between LOC and CC raises
has several direct implications for software maintainers
and evolution management.
CC has no (or very little) explanatory power of its own.
This implies that indicators that rely on CC may more
easily be calculated and normalized by using LOC. Cal-
culation of CC requires some cost however small. The
results from this study indicate there is no more insight
gained from CC when compared to LOC.
The relationship between CC and LOC is near linear
regardless of language type for the three languages in this
study. This result implies that the characteristic of com-
plexity and test case size measured by CC and LOC is the
same in a procedural language (C), an objected-oriented
language (Java) and a hybrid language (C++). It also im-
plies that if CC indeed measures some aspects of com-
plexity, then developers tend to add these aspects to a
program at an incredibly steady rate (at least in practice).
Modules where LOC does not predict CC are outliers
and should be targeted for closer scrutiny. These models
on average accounted for 90% of CC’s variance. This
means that any source-file/program which does not fit
this model is in a statistical sense an outlier. If the outlier
status of these modules to the model is equally (or even
partially) indicative of a similar status for true complex-
ity then these linear models themselves can be used as a
form of complexity metric or at least as a monitor for
possible complexity issues. Modules where LOC does
not predict CC (or vice-versa) may indicate an overly-
complex module with a high density of decision points or

Cycloma t ic Complexity and Lines of Code: Empirical Evidence of a Stable Linear Relationship143
an overly-simple module that may need to be refactored.
We plan to pursue this line of inquiry in future work.
7. Conclusions
We carried out a large empirical study of the relationship
between LOC and CC for a sample population that
crossed languages, methodologies, and programming
paradigms. We found that due mostly to issues regarding
population variance, that the linearity of the relationship
between these two measurements has been severely un-
derestimated. Using modern statistical tools we develop
linear models that can account for the majority of CC by
LOC alone. We conclude that CC has no explanatory
power of its own and th at LOC and CC measure th e same
property. We also conclude that if CC does have any va-
lidity as a measure of either complexity or test space size,
then we must conclude these factors grow linearly with
size regardless of software language, paradigm, or meth-
odology. The stability of the linear relationships we
found suggests future work in examining their worth as
metrics in their own right.
REFERENCES
[1] R. D. Banker, M. D. Srikant, C. F. Kemerer, and D.
Zweig, “Software complexity and maintenance cost,”
Communications of the ACM, Vol. 36, No. 11, pp. 81–94,
1993.
[2] G. K. Gill and C. F. Kemerer, “Cyclomatic complexity
density and software maintenance productivity,” IEEE
Transactions on Software Engineering, Vol. 17, No.12, pp.
1284–1288, 1991. (REF 15)
[3] F. G. Wilkie and B. Hylands, “Measuring complexity in
C++ application software,” Software: Practice and Ex-
perience, Vol. 28, No. 5, pp. 513–546, 1998. (REF 17)
[4] B. Curtis, S. B. Sheppard and P. Milliman, “Third time
charm: Stronger prediction of programmer performance
by software complexity metrics,” Proceedings of the 4th
International Conference on Software Engineering, pp.
356–360, 1979.
[5] J. C. Munson and T. M. Khoshgoftaar. “The detection of
fault-prone programs,” IEEE Transactions on Software
Engineering, Vol. 18, No. 5, pp. 423–433, 1992.
[6] V. R. Basili and B. T. Perricone, “Software errors and
complexity: An empirical investigation,” Communica-
tions of the ACM, Vol. 27, No. 1, pp. 42–52. 1983. (REF
4)
[7] J. C. Munsona and T. M. Khoshgoftaar, “The dimension-
ality of program complexity,” Proceedings of the 11th In-
ternational Conference on Software Engineering, pp.
245–253, 1989.
[8] T. J. McCabe, “A complexity measure,” IEEE Transac-
tions on Software Engineering, Vol. 2, No. 4, pp. 308–320,
1976.
[9] M. Shepperd, “A critique of cyclomatic complexity as a
software metric,” Software Engineering Journal, Vol. 3,
No. 2, pp. 30–36, 1988.
[10] A. R. Feuer and E. B. Fowlkes, “Some results from an
empirical study of computer software,” Proceedings of the
4th Internation al Co nferenc e on Softw are Engine ering, pp.
351–355, 1979. (REF 6)
[11] R. Subramanyam and M. S. Krishnan, “Empirical analysis
of CK metrics for object-oriented design complexity: Im-
plications for software defects,” IEEE Transactions on
Software Engineering, Vol. 29, No. 4, pp. 297–310. 2003.
[12] W. Li, “An empirical study of software reuse in recon-
structive maintenance,” Software Maintenance: Research
and Practice, Vol. 9, pp. 69–83, 1997.
[13] S. J. Sayyad and T. J. Menzies, The PROMISE Reposi tor y
of Software Engineering Databases, School of Inf or mation
Technology and Engineering, University of Ottawa, Can-
ada, http://promise.site.uottawa.ca/SERepository.
[14] SourceForge, http://www.sourceforge.net/.
[15] Alexa, Top 500, 2007, http://www.alexa.com/.
[16] Hewlett Packard: HP-sponsored projects hosted on Source-
Forge, 2007, http://hp.sourceforge.net/.
[17] IBM, http://sourceforge.net/powerbar/websphere/.
[18] Subversion, http://subversion.tigris.org/.
[19] RSM, http://www.msquaredtechnologies.com/.
[20] CCCC, C and C++ Code Counter, 2007, http://sourcefor-
ge.net/projects/cccc/.
[21] T. S. Breusch and A. R. Pagan, “A simple test for hetero-
scedasticity and random coefficient variation,” Economet-
rica, Vol. 47, No. 5, pp. 1287–1294, 1979.
[22] A. F. Siegel, “Robust regression using repeated medians,”
Biometrika, Vol. 69, No. 1, pp. 242–244, 1982.
[23] H. Zuse, “A fra mework of software measurement,” W alter
de Gruyter, New York, 1998.
[24] J. Bowen, “Are current approaches sufficient for measur-
ing software quality?” Proceedings of Software Quality
Assurance Workshop, pp. 148–155, 1978.
[25] M. R. Woodward, M. A. Hennell and D. A. Hedley, “A
measure of control flow complexity in program text,”
IEEE Transact ions on Softwar e Engineering, Vol. 5, No. 1,
pp. 45–50, 1979.
[26] M. Paige, “A metric for software test planning,” Proceed-
ings of COMPSAC 80 Conference, Buffalo, NY, pp.
499–504, Oct. 1980.
[27] T. Menzies, J. Greenwald and A. Frank. “Data mining
static code attributes to learn defect predictors,” IEEE
Transactions on Software Engineering, Vol. 33, No. 1,
2–13, 2007.