Int. J. Communications, Network and System Sciences, 2009, 7, 687-694
doi:10.4236/ijcns.2009.27079 Published Online October 2009 (http://www.SciRP.org/journal/ijcns/).
687
Augmented Reality for Realistic Simulation Using
Improved Snake and Picking Algorithm by
Proportional Relational Expression
JeongHee CHA1, GyeYoung KIM2, HyungIl CHOI3
1Division of Computer Information, School of Computing, School of Media,
2BaekSeok Culture University,Anseo Dong, DongNam Gu, Cheonan, Korea,
3Soongsil University , Sangdo 5 Dong , DongJak Gu, Seoul, Korea,
Received May 8, 2009; revised June 29, 2009; accepted August 17, 2009
ABSTRACT
In realistic simulation of mobile Augmented Reality, essential point is how to best depict occluded area in
such a way that the user can correctly infer the depth relationships between real and virtual objects. However,
if the constructed 3D map of real world is not accurate or the density is not sufficient to estimate the object
boundary, it is very difficult to determine the occluded area. In order to solve this problem, this paper pro-
poses a new method for calculating the occlusion area using the improved snake algorithm and picking algo-
rithm by the proportional relational expression. First, we generated the wireframe by the DEM in the ex-
perimental region and mapped to CCD real image using visual clues. And then, we calculated the 3D infor-
mation at the point where occlusion problem for a moving virtual target by the proposed method. Experi-
mental results show the validity of the proposed approach under the environment in which partial occlusions
occur.
Keywords: Snake, Picking, DEM, Occlusion, AR, Simulation
1. Introduction
This paper studied on the development of a realistic
simulated training model through the display of virtual
targets in the input images of CCD camera mounted in a
vehicle and the determination of occlusion areas gener-
ated from the creation and movement of virtual objects
through a movement path according to a scenario. Aug-
mented reality has three general characteristics: image
registration, interaction, and real time [1,2]. Image regis-
tration refers to the matching of the locations of the real
world object that user watch and the related virtual object.
Interaction implies that the combination of virtual objects
and the objects in real images must be harmonized with
surrounding environment in a realistic manner, and refers
to the determination of occlusion areas according to the
changed location or line of sight of the observer or the
re-rendering of virtual objects after detection of colli-
sions. Real time refers to the real time image registration
and interaction. A key problem in the AR field is how to
best depict occluded objects in such a way that the
viewer can correctly infer the depth relationships between
different real and virtual objects. For occlusion process-
ing such as the hiding of farther virtual objects by closer
real objects and the covering of objects in real images by
other virtual objects, the two worlds must be accurately
coordinated and then the depth of the actual scene must
be compared with the depth of virtual objects [3,4]. But
if the accuracy or density of the created map is insuffi-
cient to estimate the boundary of occlusion area, it is
difficult to determine the occlusion area. To solve this
problem, first, we created a 3D wireframe using the
DEM of the experiment area and then coordinate this to
CCD camera images using visual clues. Second, to solve
the problem of occlusion by accurately estimating the
boundary regardless of the density of map, this paper
also proposed a method to obtain the reference 3D in-
formation of the occlusion points using the improved
Snake algorithm and the Picking algorithm and then to
infer the 3D information of other boundaries using the
proportional relations between 2D and 3D DEM. Third,
for improving processing speed, we suggest a method by
comparing the MER (Minimum Enclosing Rectangle)
area of the real object in the camera’s angle of view and

J. H. CHA ET AL. 688
the MER of the virtual target.
We briefly review related work in Section 2. In Sec-
tion 3, we outline the framework of our proposed algo-
rithm. The methodology of Wireframe modeling, im-
proved snake algorithm for extracting image boundary
and picking algorithm for acquiring 3D information are
explained in Section 4. Section 5, we show the experi-
mental results and the validity of the proposed approach.
Finally, in Section 6 we discuss drawbacks of the algo-
rithm and propose possible future work.
2. Previous Work
A basic design decision in building an AR system is how
to accomplish the combining of real and virtual. Toward
this purpose, many researchers make efforts to minimize
virtual objects registration error and to increase the real-
ness of virtual objects [5]. Drastic and Milgram list a
number of cues that a user may use to interpret depth,
including image resolution and clarity, contrast and lu-
minance, occlusion, depth of field and accommodation
[6]. We can use one of two technologies to see the real
world in AR, one is optical see-through and the other is
video see-through. These technologies can present oc-
cluded objects, and each has a variety of challenges [7].
Blurring also can help compensate for depth perception
errors [8]. Koch uses computer vision techniques to infer
dense and accurate depth maps from image pairs, and
uses this information to construct 3D graphical represen-
tations of the restricted static environment [9]. Several
authors observe that providing correct occlusion of real
objects by virtual objects requires a scene model. Correct
occlusion relationships do not necessarily need to be
displayed at all pixels. The purpose of many applications
is to see through real object. We introduce here mobile
vehicle-mounted display system capable of resolving
occlusion between real and virtual objects. We restricted
the real environment to some area and constructed that
area’s scene Model using 3D information. The heart of
our system is boundary extraction algorithm and 3D in-
formation inference algorithm of object boundary. Figure
1 shows our monitor-based training vehicle configura-
tion.
In our experimental vehicle configurations, we send
steering, acceleration, brake data to car driving controller
through Bluetooth using remote car controller. Vehicle
can be controlled by transmitted data and we can get
feedback of present car location data by mounted sensor
system. RS232 communicator is interface between vehi-
cle driving controller and sensor fusion system. And it
receives instructions from sensor system. CCD camera
views the environment. The camera may be static or mo-
bile. In mobile case, the camera might move around by
being attached to a vehicle, with their locations tracked
by GPS and INS. The image of real world and the virtual
images generated by a scene generator are combined.
3. System Flow Description
Figure 2 outlines the framework of our proposed system.
System has two stages. First stage is environment map
construction stage. It consists of registration of two
world using visual clues and object contour extraction
and acquiring 3D information. Second stage is virtual
object rendering stage. It has creation of virtual target
path and selection of candidate occlusion object and oc-
clusion processing.
4. Methodology
4.1. Formation of Wireframe Using DEM and
Registration with Real Images Using Visual
Clues
The topographical information DEM (Digital Elevation
Figure 1. Training vehicle configuration.

J. H. CHA ET AL. 689
Model) is used to map the real world coordinates to each
point of the 2D CCD image. DEM has information on
the latitude and longitude coordinates expressed in X and
Y and heights in fixed interval. The DEM used for this
experiment is a grid-type DEM which had been produced
to have the height information for 2D coordinates in 1M
interval for the limited experiment area of 300 m x 300
m. The DEM data are read to create a mesh with the ver-
texes of each rectangle and a wireframe with 3D depth
information [10,11] as Figure 3. This is overlaid on the
sensor image to check the coordination, and visual clues
are used to move the image to up, down, left or right as
shown in Figure 4, thus reducing error. Based on this
initial coordinated location, the location changes by
movement of vehicles were frequently updated using
GPS (Global Positioning System) and INS (Inertial Navi-
gation System).
4.2. Extracting the Contour of Objects in Image
by Enhanced Snake Algorithm
4.2.1. Edge Map Using Gradient Vector Flow
The Snake algorithm [12,13] is a method of finding the
outline of an object by repeatedly moving to the direction
of minimizing energy function from the snake vertex
input by user. But existing snake algorithm cannot accu-
rately extract the contour information when the object
form is complex because as shown in Figure 5, the direc-
tion of the energy function appears as a composite vector
of the current, previous, and the next snake points, and
shrinks toward the center of these points. To solve this
problem, this paper proposes a method to form an edge
Figure 2. Proposed system framework.
Figure 3. Wireframe creation using DEM.
Figure 4. Registration of two worlds using visual clues.
Figure 5. The direction of energy minimization search in
snake algorithm.
map using the Gradient Vector Flow (GVF) algorithm
[14,15,16], and add a new energy term that indicates the
distance between the searched edge point and snake
point so as to extract an accurate contour.
The GVF algorithm can measure the contour of com-
plex objects using the gradient of edge, and move to the
concave contour regardless of initialization. Further, the
gradient vector of the edge map has a larger value as it is
near edge, and approaches zero as it is farther. This paper
uses the edge information of the gradient vector flow to
search the proximal edge point, and when there is an
edge, adds a new energy term(Eedge-distance) that shows the
dis tance from the reference point to the searched edge as
Equation (1). Here, α β, and γ are all set to 1 without
exhaustive adjustment .
1
0
tan
(()) (())
(()) (())
snake continuitycurvature
imageedge disce
EEvsEvs
EvsE vsds



 (1)
4.2.2. The Proximal Edge Search Method
Figure 6 shows a proposed proximal edge search method
in this paper.
First it searches edge points while rotating around the
axis d which is the connection between current and pre-
vious snake points vi and vi-1. In other words, if the angle
formed by the three points vi, vi-1, and vi-2 is

, to pre-
vent the situation where the axis meets with or passes by
vi-2 and meets vi again, it searches the edge point
where the image strength
▽I is greater than the thresh-
old while rotating only by
'
i
v
2

and adds a new energy
term using the value of the distance d’ between vi and '
to the existing algorithm. This paper determined the rotation
i
v

J. H. CHA ET AL. 690
direction for accurate search by assuming the following
two facts: First, it was assumed that the initial snake
points form a closed curve that encloses the object. Sec-
ond, it was assumed that the points were arranged se-
quentially in one direction. The reason for this was be-
cause to search proximal edge, it must move inside the
contour, but the direction may be wrong due to the di-
versity of object forms if simply the direction to the ob-
ject center is set. Figure 7 is an example of setting the
rotation direction of the snake points.
4.2.3. Calc ul a tion of Eedge-distance
Figure 8 is an example of calculating the distance be-
tween an arbitrary snake point vi and the edge around
it. If we surround the arbitrary point vi with a 9×9 win-
dow and assume that its distance with a new edge is ,
the height and width of the window are s, and the hori-
zontal and vertical positions of the snake point in the
window are m and n, the can be obtained with the
Equation (2) by the Euclidean theorem, and the energy
term to be added can be defined as the Equation (3) by
applying the distance value instead of the brightness
value of the image term.
'
i
v
'
mn
d
'
mn
d
22
''
'2() 12() 1
22
xx yy
mn
vv msvvns
d

 








(2)
''' '
minmax min
''' '
()/(
()/( )
edge distanceii
mn minmax min
Evvdd
ddd d
 
 
)d
(3)
Added new energy term Eedge-distance is expressed to-
gether with continuity and curvature energy terms in
Figure 9. When only the two terms of the existing algo-
rithm were considered, the minimum point of energy was
in line 3, column 5, but the location changed to line 4,
column 6 when the energy value in consideration of the
distance between proximal edges was included. In con-
clusion, the flow of the enhanced snake energy function
to which the proximal edge energy function is added can
extract the edge exactly in complex situations by ap-
proaching the edge more closely.
Table 1 shows the pseudo codes of the proposed algo-
rithm using proximal edge search method.
4.3. Acquisition of 3D Information Using the
Picking Algorithm
In order to acquire the 3D information of the extracted
vertexes, this paper used the Picking algorithm which is
a well-known 3D graphics technique [17]. It finds the
collision point with the 3D wireframe created by DEM
that corresponds to the points in 2D image and provides
the 3D information of the points. The picking search
point is the lowest point of the vertexes of the objects
Figure 6. The proximal edge search method.
Figure 7. Snake’s rotation direction.
Figure 8. Distance between a point of snake and edge.
Figure 9. Changed energy minimization point by proposed
algorithm.

A. SHABAN ET AL.
691
Table 1. Pseudo codes of proposed algorithm.
Do /* loop for proposed algorithm */
For i=0 to n-1 /* n is number of snake points */
Angle = ; /* search limit determination */
2/)( 12 iii vvv  
for j = 0 to Angle
if is Edge then bFind = true;
'
i
v
BIGE 
min ;
for j = 0 to m-1 /* m is size of neighborhood */
if bFind is True then
jancedistedgejimagejcurvjcontjEEEEE ,,,, 


 ;
Else ;
jimagejcurvjcontj EEEE ,,, 
If then
inmj EE
jinm
E
E
;
j
j

min ;
move point to location ;
if (
i
vinm j
inm
j
!= current location) cnt_movedpoint += 1;
/* following process determines where to allow corners */
For i=0 to n-1
2
11 // 
 iiiii uuuuc ;
For i=0 to n-1
If and ;
1
ii cc1 ii cc
/* if ci(curvature) is larger than neighborhood’s */
and threshold1 ;/* if ci is larger than threshold1 */ 
i
c
and )( i
v
mag threshold2;
/* if edge strength is larger than threshold2 */
Then =0; /* relax curvature at point i */
i

Until cnt_movedpoint < threshold3;
extracted from the 2D image. The screen coordinate sys-
tem that is a rectangular area indicating a figure that has
been projection transformed in the 3D image rendering
process must be converted to the viewport coordinate
system in which the actual 3D topography exists to pick
the coordinate system where the mouse is actually pre-
sent. First, the conversion matrix to convert viewport to
screen is used to obtain the conversion formula from 2D
screen to 3D projection window, and then the ray of light
is lengthened gradually from the projection window to
the ground surface to obtain the collision point between
Figure 10. 3D information extraction using collision point of
ray and DEM. (a)occlusion candidate (b)matching ref.point
and DEM (c)3D information extraction.
the point to search and the ground surface. Figure 10 is
an example of picking the collision point between the ray
of light and DEM. The lowest point of the occlusion area
indicated by an arrow is the reference point to search,
and this becomes the actual position value of 2D image
in a 3D space.
4.3.1. Creation of 3D Information Using Proportional
Relational Expression
The collision point, or reference point, has 3D coordi-
nates in DEM, but other vertexes of the snake indicated
as object outline cannot obtain 3D coordinates because
they don’t have a collision point. Therefore, this paper
suggested obtaining a proportional relation between 2D
image and 3D DEM using the collision reference point
and then obtaining the 3D coordinates of another vertex.
Figure 11 shows the proportional relation between 2D
and 3D vertexes. In Figure 11,m
S
is center of screen,
B
S
is reference point of snake vertexes (lowest point),
),( BB yx SS
B
S




is a distance from to , is a
optional point except reference point of snake vertexes,
m
SB
Sk
S
),( kk yxSS
k
S




is a distance from to .
m
Sk Sm
P
is
a projection point of straight line of B
P
in 3D, which is
through the center of screen. B
P
is a 3D correspondence
point of ,
B
SP),, z
P,( B
xB PBB y
P



k
P
is a optional
point except reference point, )
k,k
z
P,k
y
P(xk P P


 ,
,
BOPPt , mom PPt '
:tt
B

, . : a projected
vector of t to xz plane.
m
t
B
 t:''
t
To get m
p
in 3D that passes the center of the screen
using the coordinates of the reference point obtained
above, must be obtained first. As the t value is given
by the picking ray, the given t value and yB are used to
get θB and is obtained using thisθB in Expression (4).
'
t
'
t
Figure 11. Proportional relation of the vertexes in 2D and
3D.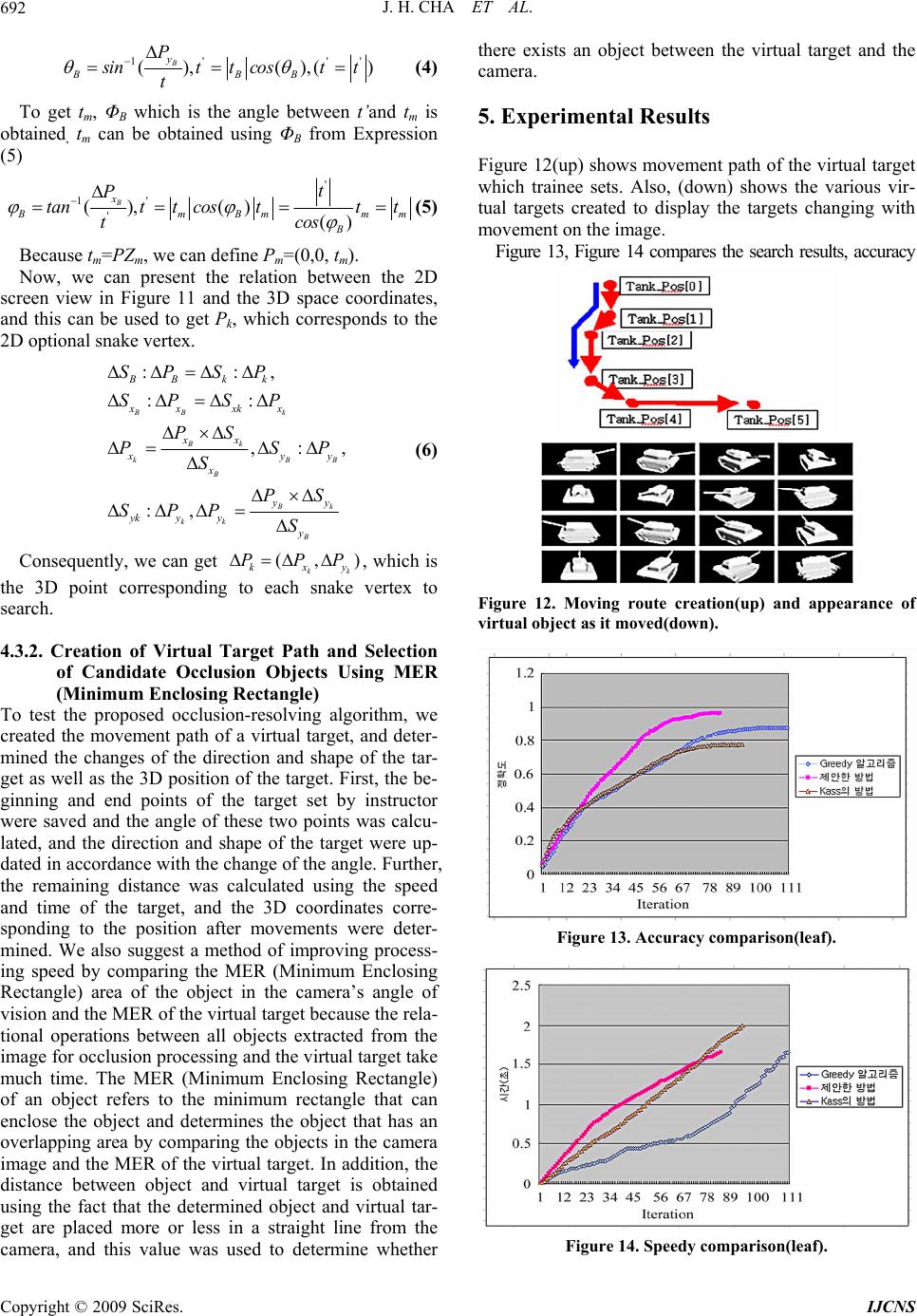

J. H. CHA ET AL. 692
1' '
(),(),(
B
y
BBB
P'
)
s
intt costt
t



 (4)
To get tm, ΦB which is the angle between t’and tm is
obtained, tm can be obtained using ΦB from Expression
(5)
'
1'
'
(),() ()
B
x
B
mBmm
B
t P
tantt costtt
cos t




m

(5)
Because tm=PZm, we can define Pm=(0,0, tm).
Now, we can present the relation between the 2D
screen view in Figure 11 and the 3D space coordinates,
and this can be used to get Pk, which corresponds to the
2D optional snake vertex.
::,
::
,:
:,
BB k
Bk
k
B
Bk
kk
B
BB kk
xx xkx
xx ,
B B
x
yy
x
yy
yk y y
y
SP SP
SP SP
PS
PS
S
PS
SPPS



 




P
(6)
Consequently, we can get ),(kk yxk PPP 

, which is
the 3D point corresponding to each snake vertex to
search.
4.3.2. Creation of Virtual Target Path and Selection
of Candidate Occlusion Objects Using MER
(Minimum Enclosing Rectangle)
To test the proposed occlusion-resolving algorithm, we
created the movement path of a virtual target, and deter-
mined the changes of the direction and shape of the tar-
get as well as the 3D position of the target. First, the be-
ginning and end points of the target set by instructor
were saved and the angle of these two points was calcu-
lated, and the direction and shape of the target were up-
dated in accordance with the change of the angle. Further,
the remaining distance was calculated using the speed
and time of the target, and the 3D coordinates corre-
sponding to the position after movements were deter-
mined. We also suggest a method of improving process-
ing speed by comparing the MER (Minimum Enclosing
Rectangle) area of the object in the camera’s angle of
vision and the MER of the virtual target because the rela-
tional operations between all objects extracted from the
image for occlusion processing and the virtual target take
much time. The MER (Minimum Enclosing Rectangle)
of an object refers to the minimum rectangle that can
enclose the object and determines the object that has an
overlapping area by comparing the objects in the camera
image and the MER of the virtual target. In addition, the
distance between object and virtual target is obtained
using the fact that the determined object and virtual tar-
get are placed more or less in a straight line from the
camera, and this value was used to determine whether
there exists an object between the virtual target and the
camera.
5. Experimental Results
Figure 12(up) shows movement path of the virtual target
which trainee sets. Also, (down) shows the various vir-
tual targets created to display the targets changing with
movement on the image.
Figure 13, Figure 14 compares the search results, accuracy
Figure 12. Moving route creation(up) and appearance of
virtual object as it moved(down).
Figure 13. Accuracy comparison(leaf).
Figure 14. Speedy comparison(leaf).

J. H. CHA ET AL. 693
Figure 15. Experimental results of moving and occlusion.
and speed for more complex leaf. As shown in the fig-
ures and graphs, we can see that the proposed algo rithm
has much higher accuracy and less repetition counts, and
the speed is equal to greedy algorithm.
As shown in Figure 13, the proposed algorithm
stopped search at the 80th round, and the accuracy was
0.96 while the Kass and greedy algorithms showed the
search count 96 and 150 and the accuracy 0.78 and 0.84,
respectively. Therefore, we can conclude that the pro-
posed algorithm has higher performance than existing
algorithms. The search speed of the proposed algorithm
was 1.65 seconds, which is equal level to the greedy al-
gorithms.
Figure 15 shows the virtual images moving along the
path by frame. We can see that as the frames increase, it
is occluded between the tank and the object.
Table 3 compares between the case of using snake ver-
texes to select objects in the image to compare with vir-
tual targets and the case of using the proposed MER.
With the proposed method, the processing speed de-
creased by 1.671, which contributed to performance im-
provement.
6. Conclusions
To efficiently solve the problem of occlusion that occurs
when virtual targets are moved along the specified path
over an actual image, we created 3D virtual world using
DEM and coordinated this using camera images and vis-
ual clues. Moreover, the enhanced Snake algorithm and
the Picking algorithm were used to extract an object that
Table 3. Speed comparison.
Method Total
frame
Used
object
Speed(se
c)
Frame per
sec.
Snake ver-
texes 301 10 112 2.687
MER(propos
ed) 301 10 67 4.492
is close to the original shape to determine the 3D infor-
mation of the point to be occluded. To increase the oc-
clusion processing speed, this paper also used the method
of using the 3D information of the MER area of the ob-
ject, and proved the validity of the proposed method
through experiment. In the future, more research is re-
quired on a more accurate extracting method for occlu-
sion area that is robust against illumination as well as on
the improvement of operation speed. We also hope to
study more in real time environment and to overcome
complicated factors that were beyond our control, such
as sensor error in the current settings, the brightness dif-
ference of same image.
7. Acknowledgement
This Work was supported by the Korea Research Foun-
dation Grant (KRF-2006-005-J03801) Funded by Korean
Government.
8. References
[1] R. Azuma, “A survey of augmented reality,” in ACM
SIGGRAPH’95 Course Note #9-Deveoping Advanced
Virtual Reality Applications, August 1995.
[2] O. Bimber and R. Raskar, “Spatial augmented reality: A
modern approach to augmented reality,” Siggraph, Los
Angeles, USA, 2005,
[3] J. Y. Noh and U. Neumann. “Expression cloning,” In
SIGGRAPH’01, pp. 277–288, 2001.
[4] E. Chen. “QuickTime VR—An image-based approach to
virtual environment navigation,” Proc. of SIGGRAPH,
1995.
[5] A. Ronald and G. Bishop. “Improving static and dynamic
registration in an optical see-through HMD,” Proceedings
of SIGGRAPH’94, Orlando, Florida, In Computer
Graphics Proceedings, Annual Conference Series pp.
197–204, July 24-29, 1994.
[6] D. Drastic and P. Milgram, “Perceptional issues in aug-

J. H. CHA ET AL. 694
mented reality,” In M. T. Bolas, S. S. Fisher, and J. O.
Merritt, editors, SPIE Volume 2653: Stereoscopic Dis-
plays and Virtual Reality Systems Ⅲ , pp. 123–134, Janu-
ary-February 1996.
[7] J. P. Rolland and H. Fuchs, “Optical versus video
see-through head-mounted displays in medical visualiza-
tion.” Presence: Teleoperators and Virtual Environments,
Vol. 9, No. 3, pp. 287–309, June 2000.
[8] A. Fuhrmann, G. Hesina, F. Faure, and M. Gervautz,
“Occlusion in collaborative augmented environments,”
Computers and Graphics, Vol. 23, No. 6, pp. 809–819,
1999
[9] K. Reinhard, “Automatic reconstruction of buildings
from stereoscopic image sequences,” In R. J. Hubbold
and R. Juan, editors, Eurographics’93, Eurographics,
Blackwell Publishers, Oxford, UK, pp. 339–350, 1993..
[10] S. Growe, P. Schulze, and R. Tnjes, “3D visualization
and evaluation of remote sensing data,” Computer Graph-
ics International’98 Hanover, Germany, June 22–26,
1998.
[11] E. Chen. “QuickTime VR—An image-based approach to
virtual environment navigation,” Proc. of SIGGRAPH,
1995.
[12] L. L. Ji and H. Yan, “Attractable snakes based on the
greedy algorithm for contour extraction,” Pattern Recog-
nition 35, pp. 791–806, 2002.
[13] C. C. H. Lean, A. K. B. See, and S. A. Shanmugam, “An
enhanced method for the snake algorithm,” First Interna-
tional Conference on Innovative Computing, Information
and Control (ICICIC’06), Vol. 1, , pp. 240–243, 2006
[14] C. Xu and J. L. Prince, “Gradient vector flow: A new
external force for snakes,” Proc. IEEE Conf. on Comp.
Vis. Patt. Recog. (CVPR), Los Alamitos: Comp. Soc.
Press, pp. 66–71, 1997.
[15] C. Y. Xu and J. L. Prince, “Snakes, Shapes, and Gradient
vector fow,” IEEE Transactions in Image Processing, Vol.
7, No. 3, Mar. 1998.
[16] C. Y. Xu and J. L. Prince, “Generalized gradient vector
flow external frces for active contours,” Signal Process-
ing, Vol. 71, No. 2, pp. 131–139, Dec. 1998.
[17] S.-T. Wu, M. Abrantes, D. Tost, and H. C. Batagelo,
“Picking and snapping for 3D input devices,” In Pro-
ceedings of SIBGRAPI’03, pp. 140–147, 2003.