 Applied Mathematics, 2011, 2, 1252-1257 doi:10.4236/am.2011.210174 Published Online October 2011 (http://www.SciRP.org/journal/am) Copyright © 2011 SciRes. AM A New Definition for Generalized First Derivative of Nonsmooth Functions Ali Vahidian Kamyad, Mohammad Hadi Noori Skandari, Hamid Reza Erfanian Department of Ap pl i e d M athematics, School of Mathematical Sciences, Ferdowsi University of Mashhad, Mashhad, Iran E-mail: {avkamyad, hadinoori344, erfanianhamidreza}@yahoo.com Received July 26, 2011; revised August 29, 2011; accepted September 6, 2011 Abstract In this paper, we define a functional optimization problem corresponding to smooth functions which its op- timal solution is first derivative of these functions in a domain. These functional optimization problems are applied for non-smooth functions which by solving these problems we obtain a kind of generalized first de- rivatives. For this purpose, a linear programming problem corresponding functional optimization problem is obtained which their optimal solutions give the approximate generalized first derivative. We show the effi- ciency of our approach by obtaining derivative and generalized derivative of some smooth and nonsmooth functions respectively in some illustrative examples. Keywords: Generalized Derivative, Smooth and Nonsmooth Functions, Fourier analysis, Linear Programming, Functional Optimization 1. Introduction The generalized derivative has played an increasingly important role in several areas of application, notably in optimization, calculus of variations, differential equa- tions, Mechanics, and control theory (see [1-3]). Some of known generalized derivatives are the Clarke’s General- ized derivative [1], the Mordukhovich’s Coderivatives [4-8], Ioffe’s Prederivatives [9-13], the Gowda and Rav- indran H-Differentials [14], the Clarck-Rockafellar Sub- differential [15], the Michel–Penot Subdifferential [16], the Treiman’s Linear Generalized Gradients [17], and the Demyanov-Rubinov Quasidifferentials [2]. In these men- tion works, for introducing generalized derivative of non-smooth function . on interval ,ab , some restrictions and results there exist, for examples 1) The function . must be locally Lipschitz or convex. 2) We must know that the function . is non-dif- ferentiable at a fixed number , ab. 3) The obtained generalized derivative of . at , ab is a set which may be empty or including sev- eral members. 4) The directional derivative is used to introduce gen- eralized derivative. 5) The concepts limsup and liminf are applied to obtain the generalized derivative in which calculation of these is usually hard and complicated. However, in this paper, we propose a new definition for generalized first derivative (GFD) which is very use- ful for practical applications and hasn’t above restrictions and complications. We introduce an especially functional optimization problem for obtaining the GFD of nonsmooth functions. This functional optimization problem is ap- proximated with the corresponding linear programming problem that we can solve it by linear programming methods such as simplex method. The structure of this paper is as follows. In Section 2, we define the GFD of non-smooth functions which is based on functional optimization. In addition, we intro- duce the linear programming problem to obtain the ap- proximate GFD of non-smooth functions. In Section 3, we use our approach for smooth and nonsmooth func- tions in some examples. Conclusions of this paper will be stated in Section 4. 2. GFD of Nonsmooth Functions In this section, we are going to introduce a functional optimization problem that its optimal solution is the de- rivative of smooth function on interval 0,1 . For solv- ing this problem, we introduce a linear programming  A. V. KAMYAD ET AL. 1253 problem. So, by solving this problem for nonsmooth functions, we obtain an approximate derivative for these functions on interval 0,1 which is GFD. Firstly, we state the following Lemma which 0,1C is space of continuous functions on 0,1 : Lemma 2.1: Let .hC0,1 and 1 0d0xhx x for any .0,1C . We have 0hx for all 0,1 x. Proof: Consider 0 such that 0,x1 00hx . Without loss of generality, suppose . Since 0 hx 0 .0,hC1 , then there is a neighborhood 0,Nx , 0 , of 0 such that for all 0hx 0,xNx . We consider the functin 0 .C0,1 such that 0. is zero on 0,Nx 0,1 and positive on 0,Nx . Thus we have: 0d 0 1 0 ,Nx 00 d hx 0 xxhx x so which is a contradiction. Then 1 0 0 hx xdx 0hx for all 0, 1 x. □ Now we state the following theorem and prove it by Lemma 2.1 which 1 C0,1 is the space of differentiable functions with the continuous derivative on 0,1 . Theorem 2.2: Let . , .gC0,1 and 1 0vxfx vx gxdx0 for any 1 .0vC,1 where . Then we have 01vv0 1 .0,fC1 and .. g . Proof: We use integration by parts rule and conditions : 01vv0 1 0 1 0 1 0 dd 11 d vxgx xxGx x vG xx vxGx 0 d. vxG v G x dt 11 00 v x vxG 0 (1) where for each 0 x Gx gt 0, 1x xfx d0x . Since 1 0vxfx vx gx dGx Gx f x 0 x , so by relation (1), 11 00 vx v or 1 0vx fx . Put for each hx Gx 0, 1x. By Lemma 2.1, since .vC0,1 we have hx 0 for all 0, 1x, it means that . .fG. Thus 0 d x xgtt. So .fC0,1 and .. g . □ let .:sin π:0,1,1,2, kk Vv vxkxxk. Then 01 kk vv0 for all . We can extend every continuous function . k v V .vC0,1 which satisfies 00v as an odd function on 1,1. Thus, there is a Sinus expansion for this function on 1,1. Now we have the following theorem: Theorem 2.3: Let . , .0,gC1 0 and 1 0d kk vxfx vxgxx where . k vV . Then we have 1 .0,fC1 and .. g . Proof: Let 11C v.0,1:0v0Vv and .v V . Since set V is a total set for space V, There are real coefficients such that 12 ,,cc 1 kk k vxcv x for any 0,1x where . k vV . Thus, if 1 0d0 kk vxfx vxgxx , 1, 2,k then 1 0 1 d kk k k cvxfxvxgxx 0 (2) We know the series is uniformly conver- 1 . kk k cv gent to the function .v. So by relation (2) 1 011 d kk kk kk vxfxcvxgx xc 0 (3) Thus, by (3) 1 0dvxfxvxgx x 0 . (4) where 1 kk k vxcv x . Thus for any .vV the relation (4) and conditions of theorem 2.2 hold. Then we have 1 .0,fC1 and .. g . □ Now we state the following theorem and in next step use it. Theorem 2.4: Let 0 is given small number, 1 .0fC,1 and m . Then there exist 0 such that for all 1ii ,, i smm 1, 2,,im 2 d i i s iii s fxfsxsf sx (5) Proof: Since lim,1,2,, i i ixs i fx fs si xs m , so there exist 0 i s such that for all Copyright © 2011 SciRes. AM  1254 A. V. KAMYAD ET AL. , iiii xs s ,1,2,, 2 ii sfs im m i fx f xs (6) Suppose that . So for all min,1, 2,, i si 1, iii smm and , ii xss , in- 1, 2,,im equality (6) is satisfied. Thus ,, ii ii isis ssss 1, 2,,im and by inequality (6) we obtain for all , 22 iii i fxfsxsf sxs (7) Thus by integrating both sides of inequality (7) on in- terval , ii ss , we can obtain ine- quality (5). □ 1, 2,,im Now consider the continuous functions . and . such that for 1 0d kk vxfx vxgxx 0 V any . We have: . k v 1 0d,.,1,2,3, kkk vxgxxv Vk (8) where 1 0d, 1,2,3, kk vxfxxk (9) Let 0 and 0 m are two sufficiently small given number and . For given continuous func- tion x on 0,1 , we define the following func- tional optimization problem: 1 0 1 .d kk k minimize Jgv xgx x (10) d 1 .0,1,,,1,2,, i i s iii s i subject to fx fsxsgs x ii , Cs i mm m (11) where for all . . k vV1,2, 3,k Theorem 2.5: Let 1 .0,fC1 and .0gC ,1 be the optimal solution of the functional optimization problem (10)-(11). Then, . fg .. Proof: It is trivial 1 0 1 d0 kk k vxgx x for all .0,gC1. By theorem 2.3, we have 1 0d kk vxgx x 0V for all where . k v .. f on 0,1 . So 1 0 1 d0 kk k vxf xx , hence 11 00 11 0d kk kk vxf x xvxgx xd On the other hand .0,fC 1 and by theorem 2.4 function .f satisfies in constraints of problem (10)- (11). Thus, .f is optimal solution of functional op- timization (10)-(11). □ Thus, the GFD of non-smooth functions may be de- fined as follows: Definition 2.6: Let . be a continuous nonsmooth function on the interval 0,1 and be the opti- mal solution of the functional optimization problem (10)- (11). We denote the GFD of .g . by . d GF f and define as .. d Remark 2.7: Note that if GF fg. . be a smooth function then the . d GF f in definition 2.6 is . Further, if .f . be a nonsmooth function then GFD of . is an approximation for first derivative of function . . However, the functional optimization problem (10)- (11) is an infinite dimensional problem. Thus we may convert this problem to the corresponding finite dimen- sional problem. We can extend any function .0gC,1 on interval [–1,1] as Fourier series 0 1 cos πcos π 2kk n a xakxb kx x x where coefficients k a and for satisfy- ing in the following relations: k b1, 2,k 1 1 1 1 cos πd, sin πd, k k akxgx bkxgx (9) On the other hand, by Fourier analysis (see [18]) we have lim 0 k ka and . Then there exists lim 0 k kb N such that for all we have 1kN 0 k a and 0 k b . Hence, the problem (10)-(11) is approximated as the following finite dimensional problem: 1 0 1 . N kk k minimize Jgv xgxxd (13) 2, 1 .0,1,,,1,2,, i i s iii s i subject to fxfsxsgs dx ii Cs i mm m (14) Copyright © 2011 SciRes. AM 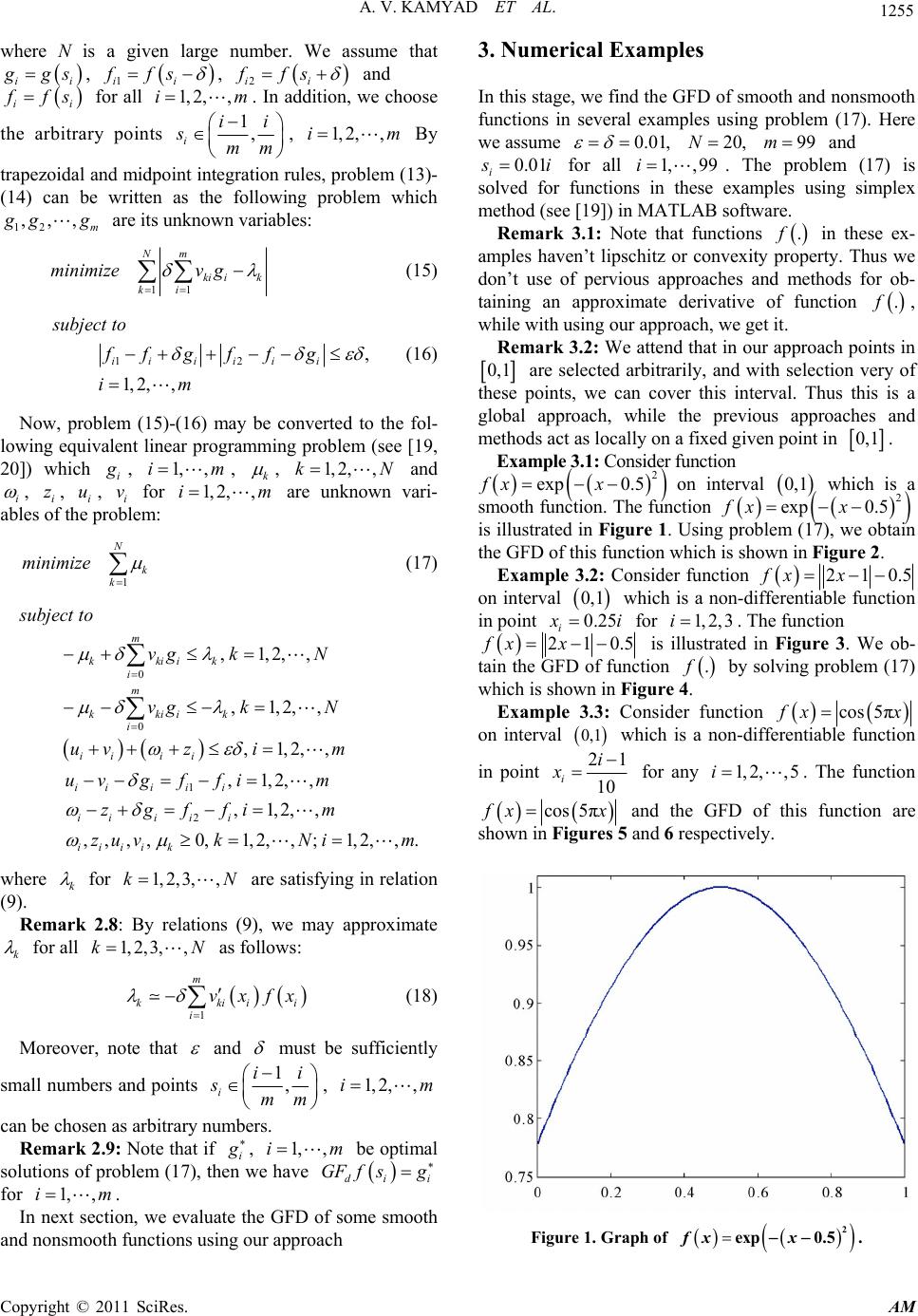 A. V. KAMYAD ET AL. 1255 where N is a given large number. We assume that ii gs, 1ii ffs , 2ii ffs and ii fs for all . In addition, we choose 1, 2,i,m the arbitrary points 1, iii smm , By 1,2, ,im trapezoidal and midpoint integration rules, problem (13)- (14) can be written as the following problem which 12 ,,, m gg are its unknown variables: 11 Nm ki ik ki minimizev g (15) 12 , 1, 2,, iii iii subject to ff gff g im (16) Now, problem (15)-(16) may be converted to the fol- lowing equivalent linear programming problem (see [19, 20]) which i , , 1, ,im k , and i 1, 2,,kN , i, i, i for are unknown vari- ables of the problem: z uv1, 2,i,m 1 N k k minimize (17) 0 0 1 2 ,1,2,, ,1,2,, ,1,2,, ,1,2,, ,1,2,, ,,,,0,1,2,,;1,2,,. m kkiik i m kkiik i ii ii iii ii iiiii iiii k subject to vg kN vg kN uvz im uvg ffim zgffim zuv kNim where k for are satisfying in relation (9). 1,2, 3,,kN Remark 2.8: By relations (9), we may approximate k for all as follows: 1,2, 3,,kN i 1 m kkii i vxfx (18) Moreover, note that and must be sufficiently small numbers and points 1, iii smm , 1, 2,,im can be chosen as arbitrary numbers. Remark 2.9: Note that if i , be optimal solutions of problem (17), then we have 1, ,im di f sgi GF for . 1, ,im In next section, we evaluate the GFD of some smooth and nonsmooth functions using our approach 3. Numerical Examples In this stage, we find the GFD of smooth and nonsmooth functions in several examples using problem (17). Here we assume 0.01, and 20,N99m 0.01 i i for all 1,i, 99 . The problem (17) is solved for functions in these examples using simplex method (see [19]) in MATLAB software. Remark 3.1: Note that functions . in these ex- amples haven’t lipschitz or convexity property. Thus we don’t use of pervious approaches and methods for ob- taining an approximate derivative of function . , while with using our approach, we get it. Remark 3.2: We attend that in our approach points in 0,1 are selected arbitrarily, and with selection very of these points, we can cover this interval. Thus this is a global approach, while the previous approaches and methods act as locally on a fixed given point in 0,1 . Example 3.1: Consider function 2 exp 0.5fx x on interval smooth function. The function is illustrated in Figure 1. Using problem (17), we obtain the GFD of this function which is shown in Figure 2. 0,1 exp which is a 2 0.5fx x Example 3.2: Consider function 210.5fx x on interval 0, 1 0.25 which is a non-differentiable function in point i i for 1, 2, 3i . The function 21x0.5fx is illustrated in Figure 3. We ob- tain the GFD of function . by solving problem (17) which is shown in Figure 4. Example 3.3: Consider function cos 5π xx on interval 0,1 which is a non-differentiable function in point 2i1 10 i x for any . The function 1,2,, 5i cos 5π xx and the GFD of this function are shown in Figures 5 and 6 respectively. Figure 1. Graph of 2 exp 0.5fx x. Copyright © 2011 SciRes. AM  1256 A. V. KAMYAD ET AL. Figure 2. Graph of . d GF for Example 3.1. Figure 3. Graph of 210.5fx x . Figure 4. Graph of . d GF for Example 3.2. Figure 5. Graph of cos 5π xx. Figure 6. Graph of . d GF for Example 3.3. 4. Conclusions In this paper, we defined a new generalized first deriva- tive (GFD) for non-smooth functions as optimal solution of a functional optimization on the interval [0,1]. We approximated this functional optimization problem by a linear programming problem. The definition of GFD in this paper has the following properties and advantages: 1) Here, the obtained GFD For smooth functions is the usual derivative of these functions. 2) In our approach, using GFD we may define the de- rivative of continuous nonsmooth functions which the other approaches are defined usually for special func- tions such as Lipschiptz or convex functions. 3) Our approach for obtaining GFD is a global ap- proach, in which the other methods and definitions are applied for one fixed known point. Copyright © 2011 SciRes. AM  A. V. KAMYAD ET AL. Copyright © 2011 SciRes. AM 1257 4) Calculating GFD by our approach is easier than other available approaches. 5. References [1] F. H. Clarke, “Optimization and Non-Smooth Analysis,” Wiley, New York, 1983. [2] V. F. Demyanov and A. M. Rubinov, “Constructive Nonsmooth Analysis,” Verlag Peter Lang, New York, 1995. [3] W. Schirotzek, “Nonsmooth Analysis,” Springer, New York, 2007. doi:10.1007/978-3-540-71333-3 [4] B. Mordukhovich, “Approximation Methods in Problems of Optimization and Control,” Nauka, Moscow, 1988. [5] B. Mordukhovich, “Complete Characterizations of Open- ness, Metric Regularity, and Lipschitzian Properties of Multifunctions,” Transactions of the American Mathe- matical Society, Vol. 340, 1993, pp. 1-35. doi:10.2307/2154544 [6] B. S. Mordukhovich, “Generalized Differential Calculus for Nonsmooth and Set-Valued Mappings,” Journal of Mathematical Analysis and Applications, Vol. 183, No. 1, 1994, pp. 250-288. doi:10.1006/jmaa.1994.1144 [7] B. Mordukhovich, “Variational Analysis and Generalized Differentiation,” Vol. 1-2, Springer, New York, 2006. [8] B. Mordukhovich, J. S. Treiman and Q. J. Zhu, “An Ex- tended Extremal Principle with Applications to Multiob- jective Optimization,” SIAM Journal on Optimization, Vol. 14, 2003, pp. 359-379. doi:10.1137/S1052623402414701 [9] A. D. Ioffe, “Nonsmooth Analysis: Differential Calculus of Nondifferentiable Mapping,” Transactions of the American Mathematical Society, Vol. 266, 1981, pp. 1-56. doi:10.1090/S0002-9947-1981-0613784-7 [10] A. D. Ioffe, “Approximate Subdifferentials and Applica- tions I: The Finite Dimensional Theory,” Transactions of the American Mathematical Society, Vol. 281, 1984, pp. 389-416. [11] A. D. Ioffe, “On the Local Surjection Property,” Nonlin- ear Analysis, Vol. 11, 1987, pp. 565-592. doi:10.1016/0362-546X(87)90073-3 [12] A. D. Ioffe, “A Lagrange Multiplier Rule with Small Convex-Valued Subdifferentials Fornonsmooth Problems of Mathematical Programming Involving Equality and Nonfunctional Constraints,” Mathematical Programming, Vol. 588, 1993, pp. 137-145. doi:10.1007/BF01581262 [13] A. D. Ioffe, “Metric Regularity and Subdifferential Cal- culus,” Russian Mathematical Surveys, Vol. 55, No. 3, 2000, pp. 501-558. doi:10.1070/RM2000v055n03ABEH000292 [14] M. S. Gowda and G. Ravindran, “Algebraic Univalence Theorems for Nonsmooth Functions,” Journal of Mathe- matical Analysis and Applications, Vol. 252, No. 2, 2000, pp. 917-935. doi:10.1006/jmaa.2000.7171 [15] R. T. Rockafellar and R. J. Wets, “Variational Analysis,” Springer, New York, 1997. [16] P. Michel and J.-P. Penot, “Calcul Sous-Diff´erentiel Pour des Fonctions Lipschitziennes et Non-Lipschitzien- nes,” CR Academic Science Paris, Ser. I Math. Vol. 298, 1985, pp. 269-272. [17] J. S. Treiman, “Lagrange Multipliers for Nonconvex Generalized Gradients with Equality, Inequality and Set Constraints,” SIAM Journal on Optimization, Vol. 37, 1999, pp. 1313-1329. doi:10.1137/S0363012996306595 [18] E. Stade, “Fourier Analysis, USA,” Wiley, New York, 2005. [19] M. S. Bazaraa, J. J. Javis and H. D. Sheralli, “Linear Pro- gramming,” Wiley & Sons, New York, 1990. [20] M. S. Bazaraa, H. D. Sheralli and C. M. Shetty, “Nonlin- ear Programming: Theory and Application,” Wiley & Sons, New York, 2006.
|