Int. J. Communications, Network and System Sciences, 2009, 7, 664-668
doi:10.4236/ijcns.2009.27076 Published Online October 2009 (http://www.SciRP.org/journal/ijcns/).
Space-Time-Frequency Coded for Multiband-OFDM
Based on IEEE 802.15.3a WPAN
Kamal MOHAMED-POUR, Hossein EBRAHIMI
Department of Electrical Engineering, K. N. Toosi University of Technology, Tehran, Iran
Received September 9, 2008; revised February 23, 2009; accepted April 15, 2009
ABSTRACT
In this paper, Multiband-OFDM UWB system based on IEEE 802.15.3a standard is studied and simulated
with spatial, time and frequency (STF)coding scheme. The using of STF coding method can guarantee both
full symbol rate and full diversity advantages. The simulation results show that the STF code uses multi-
path-rich and random-clustering characteristics of UWB channel environment on the performance of MB-
OFDM system.
Keywords: IEEE 802.15.3a, UWB, MB-OFDM, MIMO, Space-Time-Frequency Coding
1. Introduction
Ultra wideband (UWB) systems are the first nomination
for future wireless personal area networks (WPANs).
The enormous band with availability provides the poten-
tial for very high data rates. The ultra wide bandwidth of
UWB enables various WPAN applications such as high-
speed wireless universal serial bus (WUSB) connectivity
for personal computers and their accessories, high-qual-
ity real-time video and audio transmission, and cable
replacement for home entertainment systems.
Currently, the multi-band orthogonal frequency divi-
sion multiplexing (MB-OFDM) [1] is an important can-
didate for the physical layer within IEEE 802.15.3a
standard.
On the other hand, the rich scattering multipath chan-
nel in UWB indoor environment provides an ideal
transmission scenario for multiple antenna configurations.
In this paper, we use a space-time-frequency coding
(STFC) method [2] that can guarantee both full symbol
rate and full diversity for performance improvement of
MB-OFDM UWB systems over CM 1-CM 4 environ-
ment with 2ISO and 2I2O MIMO configurations.
The paper is organized as follows: In Section 2, an
overview of STFC MB-OFDM UWB system is given.
Section 3 gives the simulation results, and finally Section
4 concludes the paper.
2. STFC MB-OFDM UWB System
2.1. UWB Channel Model
The channel model is based on Saleh-Valenzuela model
[3] according to IEEE 802.15.3a standard. The channel
impulse response can be expressed as

11
,,
00
()
cc
LK ii
ii kllk
lk
htXt T  



 i
l

(1)
where i represents the realization of the i-th impulse re-
sponse, ,
i
kl

is the multipath gain coefficients, is
the delay of the l-th cluster,
i
l
T
,
i
kl

is the delay of k-th ray,
and Xi represents the log-normal shadowing. The cluster
arrivals and the path arrivals within each cluster are mod-
eled by Poisson processes




11
|exp ,
lll l
pT TTTl


0

 

(2)


,(1),, (1),
|exp ,
klklklk l
pk  


0

 

where Λ and λ (where λ >Λ) are the cluster arrival rate
and ray arrival rate, respectively. Four set of channel
model (CM) parameters for different measurement envi-
ronments were defined, namely CM 1, CM 2, CM 3, and
CM 4. Table 1 provides the model parameters of CM
1-CM 4 [4].
2.2. STFC MB-OFDM Structure
We consider a UWB multiband OFDM system with fast
band-hopping rate that signal is transmitted on a frequen-
cy-band during one OFDM symbol interval, and then

K. MOHAMED-POUR ET AL. 665
Table 1. The IEEE UWB channel parameters.
Parameters CM 1 CM 2 CM 3 CM 4
Condition LOS
0-4m
NLOS
0-4m
NLOS
4-10m
NLOS
4-10m
(1/nsec) 0.0233 0.4 0.0667 0.0667

(1/nsec) 2.5 0.5 2.1 2.1
cluster decay factor 7.1 5.5 14 24
ray decay factor 4.3 6.7 7.9 12
path
N(10 dB) 12.5 15.3 24.9 41.2
path
N(85%) 20.8 33.9 64.7 123.3
moved to a different frequency-band at the next interval.
In Table 2 you can see the simulation parameters of
MB-OFDM UWB system. The data is encoded by STF
code words across Mt transmit antennas, N OFDM sub-
carriers, and K OFDM blocks. We suppose a frequency-
selective fading channels based on S-V model, between
any pair of transmit and receive antennas. Figure 1
represents the structure of system. Because of small
wavelength in UWB environment and fast frequency
hopping, consideration of independency between MIMO
channel elements is reasonable. In this case, according to
[2,5] the maximum achievable diversity is at most min
{ MtMr, rank(RT), KNMr}, where L is the number of de-
lay path and RT is the temporal correlation matrix.
We use repetition coded STF code [2] that is a full di-
versity code as follows:
1STF KSF
D

1D (3)
where 1K×1 is an all one matrix, is tensor product, and
DSF is a full diversity SF code of size N×Mt which have
been proposed in [6]. At the transmitter, the information
is jointly encoded across Mt transmit antennas, M OFDM
subcarriers, and K OFDM blocks. Each STF codeword is
a KN×Mt matrix that can be expressed as a

,1 ,2, ()
tt
TT TT
kkk kPNPMM 

 0DGGG (4)
where t
N
P
M




and is an integer smaller than
N, which determines the number of jointly encoded sub-
carriers. Also




,1 ,2
,1
**
,2 ,1
1
t
pp
kP KM
pp
xx
xx







GI (5)
where ,pk
x
s are selected from QPSK or BPSK constel-
lations. As mentioned earlier, we use repetition STFC
which is based on Alamouti’s structure. After STFC en-
coder, we add some preambles and headers for channel
estimation and frame and packet synchronization. The
baseband OFDM signal to be transmitted by i-th transmit
antenna at the k-th OFDM block can be expressed as [7]
  
1
0
()( )exp2
N
kk
ii
tn
E
xtdnjnf tT
M






CP

c
(6)
where represents the complex symbol to be
transmitted over n-th subcarrier by i-th transmit antenna
during the k-th OFDM symbol period. Finally, after fil-
tering, up conversion and band hopping, the trans-mitted
signal over i-th antenna is
()
k
i
dn

1
0
()Re()exp( 2)
Kkk
iiSYM
k
s
txtkTjf 



t
(7)
In the receiver, after frequency dehopping, down con-
verting and filtering, we have received signal at in matrix
form as [2]
t
E
M

YDHZ (8)
where D is the STF coded data, H is the MIMO channel
matrix, and Z is complex baseband noise. Because of
channel estimation pilots, we can determine H, so we
have
tt
EE
MM
  WYWDHWZDWZ (9)
where


1
H
H

WHHH . The receiver exploits a
maximum likelihood detector over received signal ma-
trix.
2
t
E
arg min
M











D=YDH (10)
Therefore, the error probability will be as

2
1
|2
r
M
etj
PQ
M







HH (11)
Table 2. The MB-OFDM UWB parameters.
Information rate 200 Mbps
Number of Subcarriers 128
Channel coding 5/8 rate convolutional
Constellation QPSK/BPSK
Data tones 100
TFFT
242.4 nsec
TCP 60.6 nsec
TGI 9.5 nsec
TSYM
312.5 nsec
Decoder Hard viterbi

K. MOHAMED-POUR ET AL. 666
Figure 1. STFC MB-OFDM UWB system.
012345678910
0
0. 05
0. 1
0. 15
0. 2
0. 25
0. 3
0. 35
0. 4
0. 45
Delay (ns)
P
ower
0 2 46 81012 14161820
0
0.05
0. 1
0.15
0. 2
0.25
0. 3
0.35
0. 4
0.45
0. 5
Dela y (n s )
P
ower
(a) (b)
05 10 15 20 25
0
0. 05
0. 1
0. 15
0. 2
0. 25
0. 3
0. 35
0. 4
0. 45
0. 5
Del a y ( ns)
Powe
r
05 10 15 20 25
0
0. 05
0.1
0. 15
0.2
0. 25
0.3
0. 35
0.4
0. 45
0.5
Del a y ( ns)
Power
(c) (d)
Figure 2. Simulated channel response; a) CM 1, b) CM 2, c) CM 3, d) CM 4.
3. Simulation Results
We performed simulations for a multiband UWB system
with N = 128 subcarriers and the subband bandwidth of
528 MHz. Each OFDM symbol was of duration 242.42
ns. After adding the cyclic prefix of length 60.61 ns and
the guard interval of length 9.47 ns, the symbol duration
became 312.5 ns. Figure 2 gives the simulated channel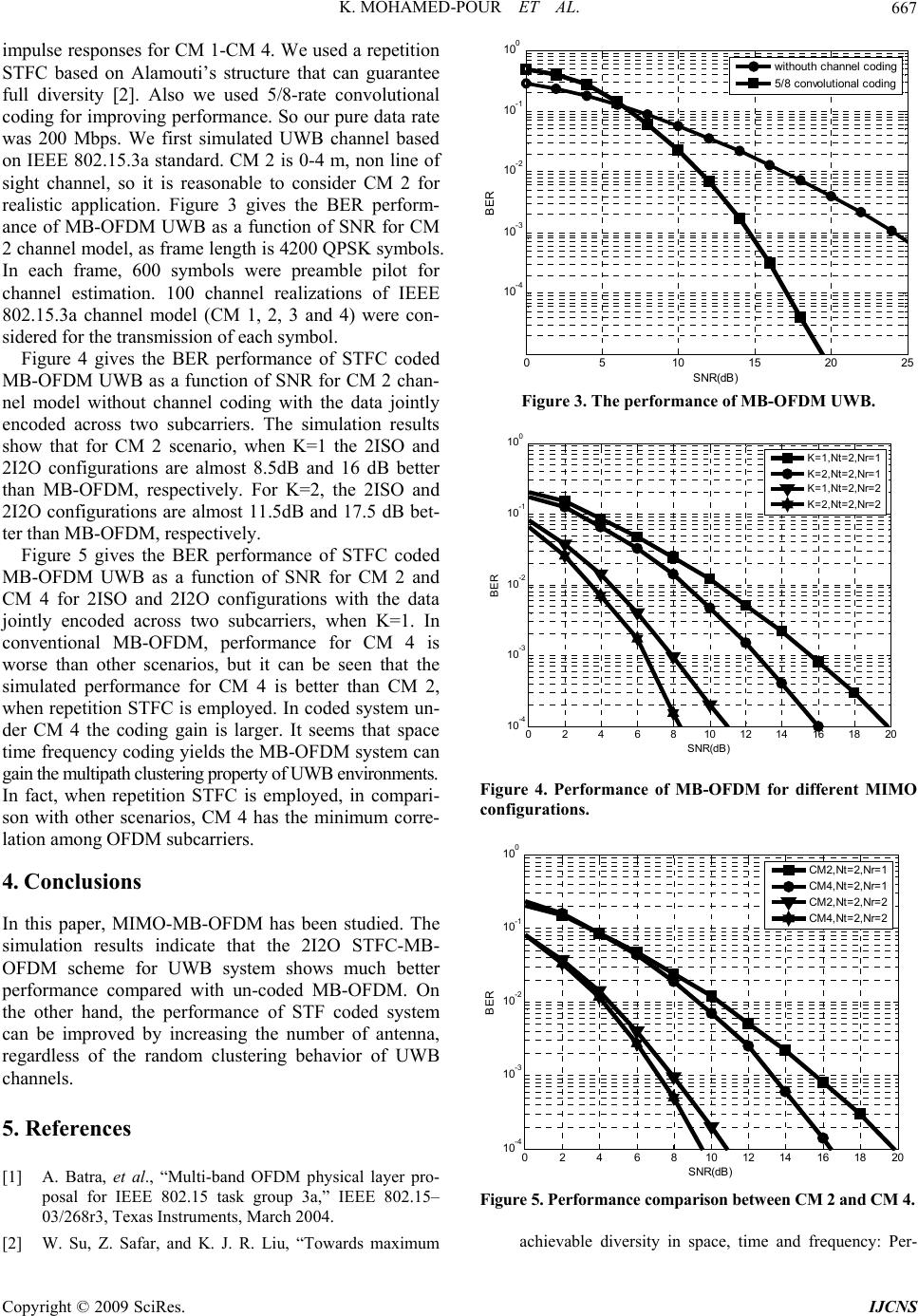

K. MOHAMED-POUR ET AL. 667
impulse responses for CM 1-CM 4. We used a repetition
STFC based on Alamouti’s structure that can guarantee
full diversity [2]. Also we used 5/8-rate convolutional
coding for improving performance. So our pure data rate
was 200 Mbps. We first simulated UWB channel based
on IEEE 802.15.3a standard. CM 2 is 0-4 m, non line of
sight channel, so it is reasonable to consider CM 2 for
realistic application. Figure 3 gives the BER perform-
ance of MB-OFDM UWB as a function of SNR for CM
2 channel model, as frame length is 4200 QPSK symbols.
In each frame, 600 symbols were preamble pilot for
channel estimation. 100 channel realizations of IEEE
802.15.3a channel model (CM 1, 2, 3 and 4) were con-
sidered for the transmission of each symbol.
Figure 4 gives the BER performance of STFC coded
MB-OFDM UWB as a function of SNR for CM 2 chan-
nel model without channel coding with the data jointly
encoded across two subcarriers. The simulation results
show that for CM 2 scenario, when K=1 the 2ISO and
2I2O configurations are almost 8.5dB and 16 dB better
than MB-OFDM, respectively. For K=2, the 2ISO and
2I2O configurations are almost 11.5dB and 17.5 dB bet-
ter than MB-OFDM, respectively.
Figure 5 gives the BER performance of STFC coded
MB-OFDM UWB as a function of SNR for CM 2 and
CM 4 for 2ISO and 2I2O configurations with the data
jointly encoded across two subcarriers, when K=1. In
conventional MB-OFDM, performance for CM 4 is
worse than other scenarios, but it can be seen that the
simulated performance for CM 4 is better than CM 2,
when repetition STFC is employed. In coded system un-
der CM 4 the coding gain is larger. It seems that space
time frequency coding yields the MB-OFDM system can
gain the multipath clustering property of UWB environments.
In fact, when repetition STFC is employed, in compari-
son with other scenarios, CM 4 has the minimum corre-
lation among OFDM subcarriers.
4. Conclusions
In this paper, MIMO-MB-OFDM has been studied. The
simulation results indicate that the 2I2O STFC-MB-
OFDM scheme for UWB system shows much better
performance compared with un-coded MB-OFDM. On
the other hand, the performance of STF coded system
can be improved by increasing the number of antenna,
regardless of the random clustering behavior of UWB
channels.
5. References
[1] A. Batra, et al., “Multi-band OFDM physical layer pro-
posal for IEEE 802.15 task group 3a,” IEEE 802.15–
03/268r3, Texas Instruments, March 2004.
[2] W. Su, Z. Safar, and K. J. R. Liu, “Towards maximum
05 1015 20 25
10
-4
10
-3
10
-2
10
-1
10
0
SNR(dB)
BER
wit houth channel codi ng
5/8 convol uti onal codi ng
Figure 3. The performance of MB-OFDM UWB.
02 4 6 810 12 1416 1820
10
-4
10
-3
10
-2
10
-1
10
0
SNR(d B)
BER
K=1,Nt=2,Nr=1
K=2,Nt=2,Nr=1
K=1,Nt=2,Nr=2
K=2,Nt=2,Nr=2
Figure 4. Performance of MB-OFDM for different MIMO
configurations.
02 46 810 12 1416 1820
10
-4
10
-3
10
-2
10
-1
10
0
SNR(dB)
BER
CM2 ,Nt=2,Nr=1
CM4 ,Nt=2,Nr=1
CM2 ,Nt=2,Nr=2
CM4 ,Nt=2,Nr=2
Figure 5. Performance comparison between CM 2 and CM 4.
achievable diversity in space, time and frequency: Per-

K. MOHAMED-POUR ET AL. 668
formance analysis and code design,” IEEE Trans. on
Wireless Commun., Vol. 4, No. 4, pp. 1847–1857, Jul.
2005.
[3] IEEE 802.15WPAN High Rate Alternative PHY Task
Group 3a (TG3a). Internet: www.ieee802.org/15/pub/
TG3a.html
[4] M. Ghavami, L. B. Michael, and R. Kohno, “Ultra wide-
band signals and systems in communication engineering,”
John Wiley & Sons, Ltd, 2004.
[5] B. Lu, X. Wang, and K. R. Narayanan, “LDPC-based
space-time coded OFDM systems over correlated fading
channels: Performance analysis and receiver design,”
IEEE Trans. Commun., Vol. 50, No. 1, pp. 74–88, Jan.
2002.
[6] W. Su, Z. Safar, M. Olfat, and K. J. R. Liu, “Obtaining
full-diversity space-frequency codes from space-time
codes via mapping,” IEEE Trans. Signal Processing, Vol.
51, pp. 2905–2916, Nov. 2003.
[7] W. P. Siriwongpairat, et al, “ Multiband-OFDM MIMO
coding framework for UWB communication systems,”
IEEE Trans. Signal Processing, Vol. 54, No. 1, Jan. 2006.