Journal of Geoscience and Environment Protection
Vol.05 No.06(2017), Article ID:77348,15 pages
10.4236/gep.2017.56017
Geographical Analysis of Lung Cancer Mortality Rate and PM2.5 Using Global Annual Average PM2.5 Grids from MODIS and MISR Aerosol Optical Depth
Zhiyong Hu*, Ethan Baker
Department of Earth & Environmental Studies, University of West Florida, Pensacola, USA




Received: May 23, 2017; Accepted: June 27, 2017; Published: June 30, 2017
ABSTRACT
Exposure to particulate matter with an aerodynamic diameter of less than 2.5 μm (PM2.5) may increase risk of lung cancer. The repetitive and broad-area coverage of satellites may allow atmospheric remote sensing to offer a unique opportunity to monitor air quality and help fill air pollution data gaps that hinder efforts to study air pollution and protect public health. This geographical study explores if there is an association between PM2.5 and lung cancer mortality rate in the conterminous USA. Lung cancer (ICD-10 codes C34- C34) death count and population at risk by county were extracted for the period from 2001 to 2010 from the U.S. CDC WONDER online database. The 2001-2010 Global Annual Average PM2.5 Grids from MODIS and MISR Aerosol Optical Depth dataset was used to calculate a 10 year average PM2.5 pollution. Exploratory spatial data analyses, spatial regression (a spatial lag and a spatial error model), and spatially extended Bayesian Monte Carlo Markov Chain simulation found that there is a significant positive association between lung cancer mortality rate and PM2.5. The association would justify the need of further toxicological investigation of the biological mechanism of the adverse effect of the PM2.5 pollution on lung cancer. The Global Annual Average PM2.5 Grids from MODIS and MISR Aerosol Optical Depth dataset provides a continuous surface of concentrations of PM2.5 and is a useful data source for environmental health research.
Keywords:
Lung Cancer, PM2.5, Remote Sensing, GIS, Exploratory Spatial Data Analysis, Spatial Regression, Bayesian MCMC Simulation

1. Introduction
Lung cancer is a leading cause of cancer mortality in the United States. Exposure to particulate matter with an aerodynamic diameter of less than 2.5 μm (PM2.5) may increase risk of lung cancer [5]. The World Health Organization (WHO) guideline for PM2.5 average annual exposure is less than or equal to 10.0 μg/m3, and the US Environmental Protection Agency (EPA) sets an annual average PM2.5 standard of 12 μg/m3. Recently findings on air pollution and lung cancer incidence in 17 European cohorts show that long term exposure to particulate air pollution increases the risk of lung cancer, even at levels below the European Union limit value (25 μg/m3) (Raaschou-Nielsen et al. 2013).
Air pollution (including PM2.5) epidemiological studies often rely on ground monitoring networks to provide metrics of exposure. Ground monitoring data often lacks spatially complete coverage. Public health concerns compel efforts to broaden spatial and temporal coverage. The repetitive and broad-area coverage of satellites may allow atmospheric remote sensing to offer a unique opportunity to monitor air quality at continental, national and regional scales. To provide a continuous surface of concentrations of PM2.5 for health and environmental research, researchers at Battelle Memorial Institute in collaboration with the Center for International Earth Science Information Network/Columbia University have developed Global Annual Average PM2.5 Grids from MODIS and MISR Aerosol Optical Depth (AOD) covering year 2001 to 2010 [3]. There are few studies using this dataset to assess PM2.5 effect on lung cancer.
This study was to examine if there is an association between PM2.5 and lung cancer mortality rate in the conterminous USA using the Global Annual Average PM2.5 Grids. The study used a suite of geographical approach, including remote sensing, GIS, cartography (map visualization and comparison), exploratory spatial data analysis (ESDA) and spatially extended statistical models.
2. Methods
2.1. PM2.5 Data
The 2001-2010 Global Annual Average PM2.5 Grids from Moderate Resolution Imaging Spectroradiometer (MODIS) and Multi-angle Imaging Spectroradiometer (MISR) Aerosol Optical Depth (AOD) dataset [3] were used to calculate a global 10-year (2001-2010) average PM2.5 grid. This global grid was then clipped to the study area―the conterminous USA.
In the Global Annual Average PM2.5 Grids data archive, each annual average data file contains integer values for a global grid (0.5˚ × 0.5˚) of estimated PM2.5 concentrations (in µg/m3) covering the world from 70˚N to 60˚S.The MODIS and MISR AOD retrievals were converted to ground-level concentrations based on a conversion factor developed by van Donkelaar et al. (2010). Level 3 global, monthly-mean MODIS and MISR AOD data for the years 2001-2010 were acquired from NASA LAADS and NASA Langley ASDC respectively. The MODIS level 3 (L3) monthly data were disaggregated from 1˚ resolution to 0.5˚ resolution to match the resolution of the MISR AOD data. AOD for both instruments that were anticipated to have a bias of greater than ±(0.1 uhuior 20%) as compared to ground-based Aerosol Robotic Network (AERONET; Holben et al. 1998) AOD due to high surface albedos or other persistent factors were removed from the analysis. The filtered MODIS and MISR data were then combined by taking the mean of each grid cell for each month of the year. Ground-level concentrations of dry 24 hour PM2.5 were estimated from the satellite observations of total-column AOD by applying a conversion factor that accounts for the spatial and temporal relationship between the two. This conversion factor is a function of aerosol size, aerosol type, diurnal variation, relative humidity and the vertical structure of aerosol extinction, which were derived from a global 3-D chemical transport model (GEOS-Chem: http://acmg.seas.harvard.edu/geos/) and assumes a relative humidity of 50% (van Donkelaar et al. 2010). The satellite AOD data were multiplied by monthly-mean conversion factors (calculated as a climatological mean over 2001-2006) for each grid cell. Finally, an annual-aver- age estimated surface PM2.5 concentration was estimated by calculating the mean of the monthly estimates over each year.
2.2. Lung Cancer Data
Lung cancer (ICD-10 codes C34-C34: malignant neoplasms of trachea, bronchus and lung) death count and population at risk by county for the conterminous USA were extracted for the period from 2001 to 2010 from the National Center for Health Statistics Compressed Mortality File 1999-2010 in the CDC WONDER online database [4]. Age adjusted rate was calculated using direct standardization for each county. The year 2000 US decennial census data was used as a standard population to standardize rates. Expected count of lung cancer was also calculated which is the number of cases that would be expected in the study population if people in the study population contracted the disease at the same rate as people in the standard population. Age-adjusted death rates are weighted averages of the age-specific death rates, where the weights represent a fixed population by age. They are used to compare relative mortality risk among groups and over time. An age-adjusted rate represents the rate that would have existed had the age-specific rates of the particular year prevailed in a population whose age distribution was the same as that of the fixed population. Age adjustment is a technique for removing the effects of age from crude rates, so as to allow meaningful comparisons across populations with different underlying age structures. Age-adjusted rates should be viewed as relative indexes rather than as direct or actual measures of mortality risk. According to Curtin and Klein [6], one of the problems with rate adjustment is that rates based on small numbers of deaths will exhibit a large amount of random variation. In the lung cancer mortality count and population data set, crude death rates and age-adjusted death rates are marked as “unreliable” when the death count is less than 20. Lung death counts are “suppressed” when the data meets the criteria for confidentiality constraints. Sub-national data representing fewer than ten persons are suppressed. All counties with unreliable and suppressed data were not included in the following spatial analyses. After excluding counties that have unreliable or suppressed data, the number of data points (counties) for the analysis is 2,931.
2.3. Exploratory Spatial Data Analysis
To link lung cancer mortality rate with PM2.5, the 10-year (2001-2010) mean PM2.5 raster grid was first resampled so that each 0.5˚ × 0.5˚ grid cell was subdivided into 20 by 20 smaller cells retaining the original PM2.5 values. The purpose of the resampling procedure was to split the grid cell on the county boundary into smaller cells for neighboring counties to achieve higher accuracy of county average PM2.5 calculation.
The resampled PM2.5 grid was then overlaid with the map of lung cancer mortality rates. A GIS zonal statistical function was used to calculate the average PM2.5 value for each county. The average value was calculated by averaging PM2.5 values of all the cells formed after the resampling of the original grid whose centroids are within the county.
Exploratory spatial data analysis (ESDA) [1] methods were used to examine the spatial autocorrelation within the spatial data and explore the association between lung cancer mortality rate and PM2.5. The analysis involved calculation of univariate global Moran’s I statistic and local indicator of spatial association (LISA) [2]. Spatial contiguity was assessed as Queen’s contiguity which defines spatial neighbors as those areas with shared borders and vertexes. Univariate global Moran’s I examines the degree of spatial autocorrelation in the mortality rate and PM2.5 maps respectively. LISA provides information relating to the location of spatial clusters and outliers and the types of spatial correlation. Local statistics are important because the magnitude of spatial autocorrelation is not necessarily uniform over the study area [1].
Univariate LISA resulted in a cluster map for each of the two variables. Bivariate LISA results were presented as a Moran scatter plot and a cluster map. Bivariate Moran’s I value determines the strength and direction of the relationship between mortality rate and PM2.5 in each county and measures the overall clustering. The Bivariate Moran’s I statistic is represented as the values of mortality rate averaged across all neighboring counties and plotted against PM2.5 in each county. If the slope on the scatter plot is significantly different to zero then there is association between mortality rate and PM2.5. Significance was tested by comparison to a reference distribution obtained by random permutations [1]. A random permutation procedure recalculates a statistic many times by reshuffling the data values among the map units to generate a reference distribution. The obtained statistic calculated based on the observed spatial pattern is then compared to this reference distribution and a pseudo significance level is computed. This analysis used 500 permutations to determine differences between spatial units.
2.4. Spatial Regression
Two regression models were fitted to examine the relationship between lung cancer mortality rate and PM2.5: Spatial lag, and spatial error. The two spatial regression models could alleviate the problem of spatial autocorrelation that might exist within the data. Spatial autocorrelation is the propensity for data values closer to each other in space to be more similar. If spatial autocorrelation exists, the assumption of independent observations and errors of classical statistical models may be violated. Spatial regression methods capture spatial dependency in regression analysis, avoiding statistical problems such as unstable parameters and unreliable significance tests, as well as providing information on spatial relationships among the variables involved. The spatial lag model (also called Spatial Auto-Regressive model, or SAR) takes the form:
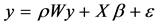 (1)
(1)
and the spatial error model takes the form:
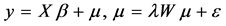 (2)
(2)
where  is an
is an 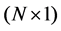 vector of observations on the dependent variable taken at each of
vector of observations on the dependent variable taken at each of 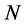 locations,
locations, 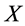 is an
is an 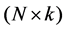 matrix of exogenous variables,
matrix of exogenous variables, 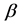 is an
is an 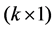 vector of parameters, and
vector of parameters, and 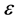 is an
is an 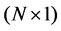 vector of disturbances,
vector of disturbances, 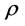 is a scalar factor for the spatial lag term,
is a scalar factor for the spatial lag term, 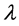 is a scalar error parameter,
is a scalar error parameter, 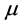 is a spatially auto-correlated disturbance vector, and
is a spatially auto-correlated disturbance vector, and 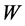 is spatial weight. The spatial weight calculation for this study was based on the first-order Queen’s contiguity rule. If two counties share boundary or node, the weight is equal to 1, otherwise it is zero. The spatial weight matrix was then row standardized so that all columns sum to 1.
is spatial weight. The spatial weight calculation for this study was based on the first-order Queen’s contiguity rule. If two counties share boundary or node, the weight is equal to 1, otherwise it is zero. The spatial weight matrix was then row standardized so that all columns sum to 1.
2.5. Lung Cancer Data Spatial Bayesian Monte Carte Markov Chain Simulation Model
The association between lung cancer mortality rate and PM2.5 was also explored using a more sophisticated spatially extended Bayesian Monte Carlo Markov Chain (MCMC) simulation model. Simulation-based algorithms for Bayesian inference allow us to fit very complicated hierarchical models, including those with spatially correlated random effects. In this geographical study, there could exist spatial autocorrelation within values of the lung cancer mortality rate and PM2.5. The following model was fitted allowing a convolution prior for the random effects:
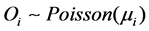 (3)
(3)
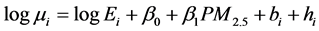 (4)
(4)
where i is the index for a county, O is observed lung cancer death count, E is expected death count reflecting age-standardized values. For model specification, an improper (flat) prior for the intercept parameter β0 and a uniform prior distribution for the fixed-effect parameters (β1) were assumed. Fixed effect means that it applies equally to all the counties. Two sets of county-specific random effects were included in the model. The first set bi is spatially structured random effects assigned an intrinsic Gaussian conditional auto-regression (CAR) prior distribution (Suwa et al. 2002). The second set of random effects hi is assigned an exchangeable (non-spatial) normal prior. The random effect for each county is thus the sum of a spatially structured component bi and an unstructured component hi. This is termed a convolution prior (Suwa et al. 2002; Best 1999). The model is more flexible than assuming only CAR random effects, since it allows the data to decide how much of the residual disease risk is due to spatially structured variation, and how much is unstructured over-dispersion. To complete the model specification, conjugate inverse-gamma prior distributions were assigned to the variance parameters associated with the exchangeable and/or CAR priors.
The MCMC simulation computation technique and Gibbs sampling algorithm were used to fit the Bayesian model. Having specified the model as a full joint distribution on all quantities, whether parameters or observables, we wish to sample values of the unknown parameters from their conditional (posterior) distribution given those stochastic nodes that have been observed. MCMC methods perform Monte Carlo simulations generating parameter values from Markov chains having stationary distributions identical to the joint posterior distribution of interest. After these Markov chains converge to a stationary distribution, the simulated parameter values represent a correlated sample of observations from the posterior distribution. The basic idea behind the Gibbs sampling algorithm is to successively sample from the conditional distribution of each node given all the others. Under broad conditions this process eventually provides samples from the joint posterior distribution of the unknown quantities. Summaries of the post-convergence MCMC samples provide posterior inference for model parameters. The result of such analysis is the posterior distribution of a density function with covariate effects.
The model was fitted using the WinBUGS software?an interactive Windows version of the BUGS (Bayesian inference Using Gibbs Sampling) program for Bayesian analysis of complex statistical models using MCMC techniques [10]. A queen’s case spatial adjacency matrix (wij = 1 when county i and j share a boundary or a vertice, wij = 0 otherwise) that is required as input for the conditional autoregressive distribution was created using the Adjacency for WinBUGS Tool developed by Upper Midwest Environmental Sciences Center of the US Geological Survey (USGS). Two Markov chains were simulated in the present study. The MCMC samplers were given initial values for each stochastic node. A total of 20,000 simulation iterations were run.
3. Results
Before you begin to format your paper, first write and save the content as a separate text file. Keep your text and graphic files separate until after the text has been formatted and styled. Do not use hard tabs, and limit use of hard returns to only one return at the end of a paragraph. Do not add any kind of pagination anywhere in the paper. Do not number text heads―the template will do that for you.
Finally, complete content and organizational editing before formatting. Please take note of the following items when proofreading spelling and grammar:
3.1. Maps of PM2.5 and Lung Cancer Mortality Rate
Figure 1 shows maps of PM2.5 and age adjusted lung cancer mortality rate. The PM2.5 exhibits more clustered pattern with higher values in the east. The average PM2.5 for all counties in the conterminous USA is 8.43 μg/m3. The eastern part has an average value around the EPA standard limit of 12 μg/m3.The mortality map shows some chessboard pattern but overall the east part of USA has higher mortality rate than west, same as PM2.5. Visual comparison of the two maps reveals an overall positive association between PM2.5 and lung cancer mortality rate.
3.2. ESDA
The univariate Moran’s I scatter plots for lung cancer mortality rate and PM2.5 are shown in Figure 2 and Figure 3 respectively. PM2.5 has extremely high positive spatial autocorrelation with a Moran’s I value of 0.9472 (close to 1). There are significant (p = 0.05) clusters of counties in the east which have high PM2.5 values both themselves and in the neighbours (“high-high”) and clusters of “low-low” in part of mid and west USA (Figure 4). There are few PM2.5 outliers (“high-low” or “low-high”). The lung cancer mortality rates are also positively spatial auto-correlated (Moran’s I = 0.6249, p = 0.05), but the autocorrelation is not so strong as PM2.5. The spatial autocorrelation is also revealed in the lung cancer mortality rate LISA cluster map (Figure 5). There are “high-high” clusters in the middle of the east and “low-low” clusters in the west. Special attention should be paid to the several “high-low” outliers in the west, where a county has high mortality rate but its neighbors have low average rate.
Figure 1. Maps of PM2.5 (μg/m3)and age adjusted lung cancer mortality rates by USA county.
Figure 2. PM2.5 Moran’s I scatter plot.
Figure 3. Age adjusted lung cancer mortality rate (AGEADJRATE) Moran’s I scatter plot.
The bivariate LISA cluster map is shown in Figure 6 (permutations = 500, p = 0.05). Note that this shows local patterns of spatial correlation at a county between lung cancer mortality rate and the average PM2.5 for its neighbors. Counties with significant spatial correlation are color-coded by type of spatial autocorrelation. There are clusters of ‘high-high” (high PM2.5 in a county and high
Figure 4. PM2.5 LISA cluster map.
Figure 5. Age adjusted lung cancer mortality rate LISA cluster map.
Figure 6. Bivariate LISA cluster map.
average mortality rate in it is neighbors) in the mid of the east and south, and “low-low” in the mid and west. A few clusters of “low-high” are in the mid, and “high-low” in the mid, west and north east. These spatial outlier locations, especially areas with low PM2.5 but high mortality rates, warrant further investigation to see if other factors dominate in effects on mortality. These four categories of clusters correspond to the four quadrants in the Moran scatter plot as shown in Figure 7, which is a box plot showing the distribution of the local Moran statistics across observations. The axes have been standardized such that the units correspond to standard deviations. The scatter plot figure has also been centered
Figure 7. Bivariate Moran’ I scatter plot: weighted age adjusted lung cancer mortality rate (W_AGEADJRATE) vs. PM2.5.
on the mean with the axes drawn such that the four quadrants are clearly shown. The high-high and low-low locations (positive local spatial correlation) represent spatial clusters, while the high-low and low-high locations (negative local spatial correlation) represent spatial outliers. The positive local Moran’s I value of 0.3851 (p = 0.05) indicates an overall positive spatial association and neighborhood effect between lung cancer mortality rate and PM2.5. It should be noted that the so-called spatial clusters shown on the LISA cluster map only refer to the core of the cluster [2]. The cluster is classified as such when the value at a location (either high or low) is more similar to its neighbors (as summarized by averaging the neighboring values, the spatial lag) than would be the case under spatial randomness. Any location for which this is the case is labeled on the cluster map. However, the cluster itself likely extends to the neighbors of this location as well.
3.3. Spatial Regression
Table 1 shows the spatial lag model result. Lung cancer mortality rate is positively significantly related to PM2.5 (β = 0.5319, p < 0.001). The coefficient parameter (ρ) of the spatial lag term of lung cancer mortality rate (W_LUNG) has a positive effect and is highly significant (ρ = 0.7261, p = 0.000), reflecting the spatial dependence inherent in the lung cancer mortality rate data - lung cancer mortality rate in a county is similar to the average of its neighbors. The low probability in the Breusch-Pagan test suggests that heteroskedasticity still exists
Table 1. Spatial lag regression model.
after introducing the spatial lag term. In the likelihood ratio test of the spatial lag dependence, the result is significant. Introducing the spatial lag term did not completely remove the spatial effects.
In the spatial error model (Table 2), the coefficient on the spatially correlated errors (λ) has a positive effect and is highly significant (λ = 0.7318, p = 0.0000). Like the lag model, the effect of PM2.5 remains positive and significant (β = 1.1852, p = 0.0000). The heteroskedasticity test remains significant (p < 0.05), indicating existence of heteroskedasticity. The likelihood ratio test of spatial error dependence has a significant result. Allowing the error term to be spatially correlated not only improved the model fit, but also made part of the spatial effects go away. The spatial lag model is slightly better than the spatial error model in terms of R2 and log likelihood values (0.5650 vs. 0.5620). In both models, PM2.5 explains over 56% of variation in the lung cancer mortality rate.
3.4. Bayessin MCMC Simulation Model
The Markov chains begin to converge after about 7,500 simulation runs and parameter value updates. After convergence, each simulation generates values fluctuating around within a consistent range of values representing the posterior distribution of each model parameter. Inferences were made about the parameters of the model using the simulated values on iterations 7500 to 20,000. Table 3 provides the estimated posterior mean, median, and associated 95% credible set for each of the fixed effects. A 95% credible set defines an interval having a 0.95 posterior probability of containing the parameter of interest which is assumed to be a random variable in Bayesian statistics. The 2.5%, 50% (median) and 97.5% quantiles and posterior mean were calculated via an approximate al
Table 2. Spatial error regression model.
Table 3. Bayesian Monte Carlo Markov Chain simulation modeling.
* Posterior means, medians, and 95% credible sets are based on post-convergence iterations (from iteration 7500 to 20,000). Dependent variable: lung cancer mortality rate. Fixed effects are: β0-intercept, β1?effect of PM2.5.
gorithm [11]. Summaries of the post-convergence MCMC samples provide posterior inference for model parameters. For example, the sample mean of the post-convergence sampled values for a particular model parameter provides an estimate of the marginal posterior mean and a point estimate of the parameter itself. The interval defined by the 2.5th and 97.5th quantiles of the post-conver- gence sampled values for a model parameter provides a 95% interval estimate of the parameter. Standard deviations and Monte Carlo (MC) errors were calculated to assess the accuracy of the simulation. The MC error is an estimate of the difference between the mean of the sampled values and the true posterior mean. As a rule of thumb, the simulation should be run until the Monte Carlo error for each parameter of interest is less than about 5% of the sample standard deviation. The MC errors calculated from the iterations 7500 to 20,000 for both the parameters are less than 5% of the corresponding standard deviations, suggesting an accurate posterior estimate for each parameter. In addition, Figure 8 shows the posterior parameter densities. The horizontal axis represents simulated parameter values. The vertical axis represents the density of each parameter
Figure 8. Bayesian MCMC simulation parameter posterior density curves.
value. The PM2.5 parameter value density curve and Table 3 show a positive association between PM2.5 pollution and lung cancer mortality rate. The 95% credible set covers positive values: 

4. Discussions and Conclusions
Significant positive association was found between lung cancer mortality rate and PM2.5. There is an excess risk of lung cancer mortality in areas with high PM2.5 levels. This study used a geographical/ecological approach. Ecological studies are more useful for generating and testing hypothesis (Rytkönen 2003). The statistically significant association between lung cancer mortality and PM2.5 can be taken as indicative of a potential air pollution effect. The association would justify the need of further toxicological approach for investigating the biological mechanism of the adverse effect of the PM2.5 pollution. Although the mechanism underlying the correlation between PM2.5 exposure and lung cancer has not fully elucidated, PM2.5-induced oxidative stress has been considered as an important molecular mechanism of PM2.5-mediated toxicity [7]. Harrison et al. (2004) [8] found it plausible that known chemical carcinogens are responsible for the lung cancers attributed to PM2.5 exposure but the possibility should not be ruled out that particulate matter is capable of causing lung cancer independent of the presence of known carcinogens.
Remote sensing could help fill pervasive data gaps that hinder efforts to study air pollution and protect public health. The Global Annual Average PM2.5 Grids from MODIS) and MISR Aerosol Optical Depth dataset provides a continuous surface of concentrations of PM2.5 and is a useful data source for health and environmental research.
Cite this paper
Hu, Z.Y. and Baker, E. (2017) Geographical Analysis of Lung Cancer Mortality Rate and PM2.5 Using Global Annual Average PM2.5 Grids from MODIS and MISR Aerosol Optical Depth. Journal of Geoscience and Environment Protection, 5, 183-197. https://doi.org/10.4236/gep.2017.56017
References
- 1. Anselin, L. (1995) Local Indicators of Spatial Association—LISA. Geographical analysis, 27, 93-115. https://doi.org/10.1111/j.1538-4632.1995.tb00338.x
- 2. Anselin, L., Syabri, I. and Smirnov, O. (2002) Visualizing Multivariate Spatial Correlation with Dynamically Linked Windows. New Tools for Spatial Data Analysis: Proceedings of the Specialist Meeting, Santa Barbara.
- 3. Socioeconomic Data and Applications Center (SEDAC) (2013) Global Annual Av-erage PM2.5 Grids from MODIS and MISR Aerosol Optical Depth (AOD), 2001-2010. http://sedac.ciesin.columbia.edu/data/set/sdei-global-annual-avg-pm2-5-2001-2010
- 4. Centers for Disease Control and Prevention, National Center for Health Statistics. (2013) Compressed Mortality File 1999-2010. CDC WONDER On-line Database, Compiled from Compressed Mortality File 1999-2010. http://wonder.cdc.gov/cmf-icd10.html
- 5. Chen, H., Goldberg, M.S. and Villeneuve, P.J. (2008) A Systematic Review of the Relation between Long-Term Exposure to Ambient Air Pollution and Chronic Diseases. Reviews on Environmental Health, 23, 243-297.
- 6. Curtin, L.R. and Klein, R.J. (1995) Direct Standardization (Age-Adjusted Death Rates) Statistical Notes, No. 6. National Center for Health Statistics, Hyattsville.
- 7. Deng, X., Zhang, F., Rui, W., Long, F., Wang, L., Feng, Z., Chen, D. and Ding, W. (2013) PM2.5-Induced Oxidative Stress Triggers Autophagy in Human Lung Epithelial A549 Cells. Toxicology in Vitro, 27, 1762-1770. https://doi.org/10.1016/j.tiv.2013.05.004
- 8. Harrison R.M., Smith, D.J.T. and Kibble, A.J. (2004) What is Responsible for the Carcinogenicity of PM2.5? Occupational and Environmental Medicine, 61, 799-805. https://doi.org/10.1136/oem.2003.010504
- 9. Holben, B.N., Eck, T.F., Slutsker, I., Tanré, D., Buis, J.P., Setzer, A., Vermote, E., Reagan, J.A., Kaufman, Y., Nakajima, T., Lavenu, F., Jankowiak, I. and Smirnov, A. (1998) AERONET—A Federated Instrument Network and Data Archive for Aerosol Characterization. Remote Sensing of Environment, 66, 1-16. https://doi.org/10.1016/S0034-4257(98)00031-5
- 10. Raaschou-Nielsen, O., Andersen, Z.J., Beelen, R., Samoli, E., et al. (2013) Air Pollution and Lung Cancer Incidence in 17 European Cohorts: Prospective Analyses from the European Study of Cohorts for Air Pollution Effects (ESCAPE). Lancet Oncology, 14, 813-822. https://doi.org/10.1016/S1470-2045(13)70279-1
- 11. Rytkönen, M., Moltchanova, E., Ranta, J., Taskinen, O., Tuomilehto, J. and Karvonen, M. (2003) The Incidence of Type 1 Diabetes among Children in Finland—Rural-Urban Difference. Health Place, 9, 315-325. https://doi.org/10.1016/S1353-8292(02)00064-3
- 12. Tierney, L. (1993) A Space-Efficient Recursive Procedure for Estimating a Quantile of an Unknown Distribution. SIAM Journal on Scientific Computing, 4, 706-711. https://doi.org/10.1137/0904048
- 13. van Donkelaar, A., Martin, R.V.,. Brauer, M., Kahn, R., Levy, R., Verduzco, C. and Villeneuve, P.J. (2010) Global Estimates of Exposure to Fine Particulate Matter Concentrations from Satellite-based Aerosol Optical Depth. Environmental Health Perspectives, 118, 847-588. https://doi.org/10.1289/ehp.0901623










