Int. J. Communications, Network and System Sciences, 2009, 7, 645-651
doi:10.4236/ijcns.2009.27073 Published Online October 2009 (http://www.SciRP.org/journal/ijcns/).
Efficient Techniques and Algori thms for Improving Indoor
Localization Precision on WLAN Networks Applications
Antonio del CORTE-VALIENTE1, Jose Manuel GÓMEZ-PULIDO2, Oscar GUTIÉRREZ-BLANCO2
1Computer Engineering Department; University of Alcalá, Alcalá de Henares, Madrid, Spain
2Computational Science Department, University of Alcalá, Alcalá de Henares, Madrid, Spain
Received May 26, 200 9; revised June 28, 2009; accepted August 1, 2009
ABSTRACT
This paper proposes efficient techniques that allow the deploying of high precision location applications for
indoor scenarios over Wireless Local Area Networks (WLAN). Firstly, we compare the use of radio
frequency (RF) power levels and relative time delays based on ray-tracing as detection methods to estimate
the localization of a set of mobile station using the fingerprint technique. Detection method play an important
role in applications of high frequencies techniques for locations systems based on current and emerging
standards such as Wi-Fi (802.11x) and Wi-Max (802.16x). The localization algorithm computes the Eucli-
dean distance between the samples of signals received from each unknown position and each fingerprint
stored in the database or radio-map obtained using the FASPRI simulation tool. Experimental results show
that more precision can be obtained in the localization process by means of relative delay instead of RF
power detection method. Secondly, the Euclidean distance has been compared with others similarity distance
measures. Finally, an interpolation algorithm between the fingerprinting weighing based on the distances has
been implemented in order to eliminate those fingerprints that do not contribute to the improvement in the
accuracy. These techniques allow obtaining more precision in the localization of indoor mobile devices over
WLAN networks.
Keywords: Localization, Euclidean Distance, Interpolation, Mahalanobis Distance, Faspri, Fingerprinting,
GTD
1. Introduction
In this work the problem of indoor localization based on
the signals available from the wireless devices [1,2] that
comprise the Wi-Fi and Wi-Max standards is presented.
The localization process is done by using the finger-
printing technique [3,4] that operate the relationship
between the power lev els and the relativ e delays between
signals due to multipath reflections. In comparison with
other techniques, such as angle of arrival (AOA) or time
of arrival (TOA) that present several challenges due to
multipath effects and non-line-of-sight (N-LOS) [2], the
fingerprinting technique is relatively easy to implement.
In traditional indoor localization systems based on Wi-Fi
networks, the Euclidean distance is used as a metric in
the localization process and the fingerprinting technique
is based on the power levels detected by means of the
received signal strength indicator (RSSI) parameter
available on the 802.11x standard between the radio
frequency (RF) power levels of the received signals and
the samples stored in the database or radio-map.
However, due to the development of new radio access
standards, such as Wi-Max, it is necessary to explore
new techniques to improve the precision by using
alternative detection methods. In a previous work [8] the
fingerprinting technique has been implemented using the
relative delays as fingerprint and the Euclidean distance
also as metric. More precision compared to the power
detection technique was obtained. However, the localiza-
tion precision can still be increased by using different
techniques within the fingerprinting matching process
[7,8]. Firstly, the Euclidean distance metric has been
replaced by others metrics such as Manhattan, Bray-
Curtis, Chi-Squared and Mahalanobis distances.
Secondly, an interpolation between the fingerprinting
weighing based on the distance was implemented. The
results obtained demonstrate the accuracy of these
techniques.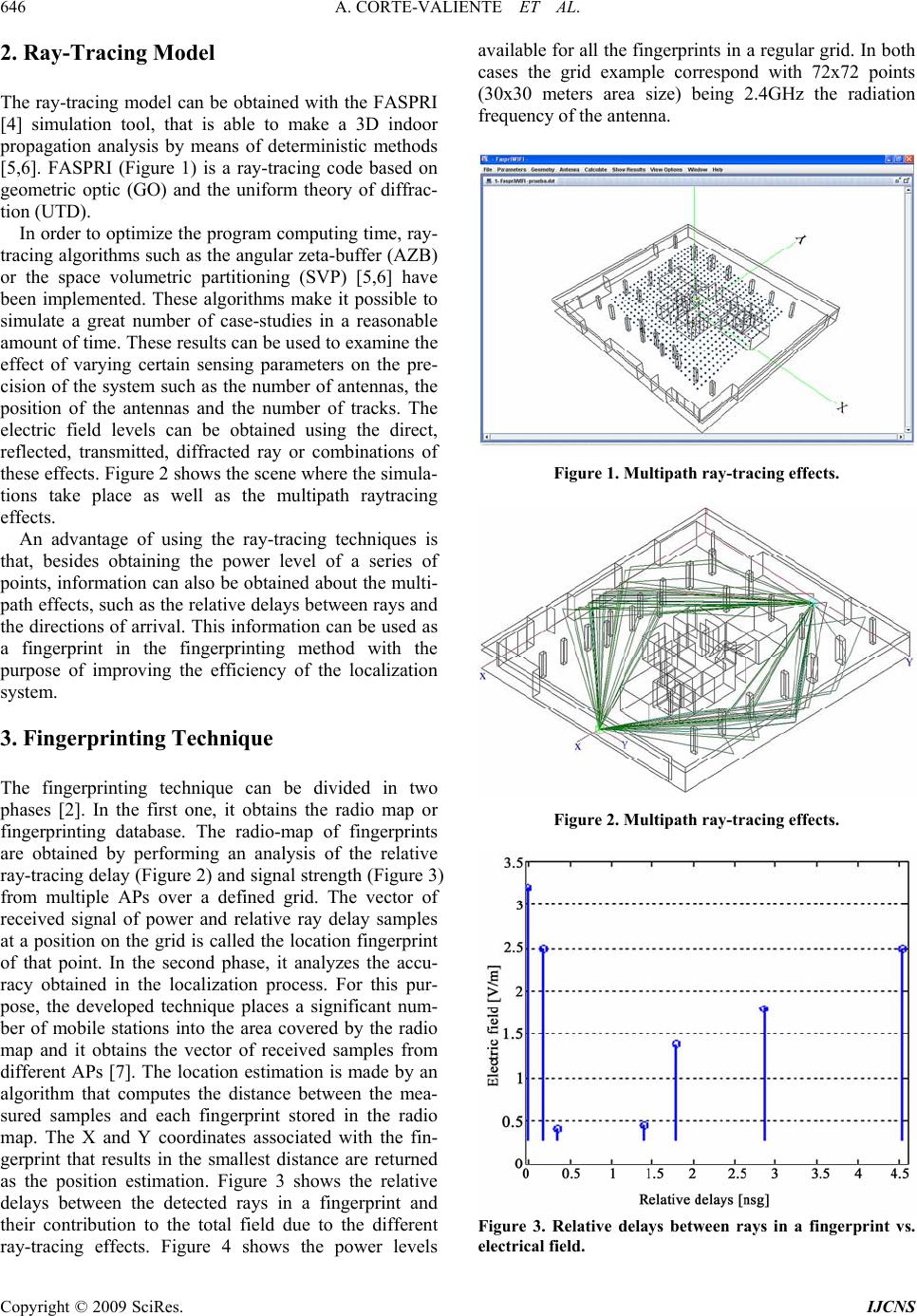

A. CORTE-VALIENTE ET AL. 646
2. Ray-Tracing Model
The ray-tracing model can be obtained with the FASPRI
[4] simulation tool, that is able to make a 3D indoor
propagation analysis by means of deterministic methods
[5,6]. FASPRI (Figure 1) is a ray-tracing code based on
geometric optic (GO) and the uniform theory of diffrac-
tion (UTD).
In order to optimize the program computing time, ray-
tracing algorithms such as the angular zeta-buffer (AZB)
or the space volumetric partitioning (SVP) [5,6] have
been implemented. These algorithms make it possible to
simulate a great number of case-studies in a reasonable
amount of time. These results can be used to examine the
effect of varying certain sensing parameters on the pre-
cision of the system such as the number of antennas, the
position of the antennas and the number of tracks. The
electric field levels can be obtained using the direct,
reflected, transmitted, diffracted ray or combinations of
these effects. Figure 2 shows the scene where the simula-
tions take place as well as the multipath raytracing
effects.
An advantage of using the ray-tracing techniques is
that, besides obtaining the power level of a series of
points, information can also be obtained about the multi-
path effects, such as the relative delays between rays and
the directions of arrival. This information can be used as
a fingerprint in the fingerprinting method with the
purpose of improving the efficiency of the localization
system.
3. Fingerprinting Technique
The fingerprinting technique can be divided in two
phases [2]. In the first one, it obtains the radio map or
fingerprinting database. The radio-map of fingerprints
are obtained by performing an analysis of the relative
ray-tracing d elay (Figu re 2) and signal strength (Figure 3)
from multiple APs over a defined grid. The vector of
received signal of power and relative ray delay samples
at a position on the grid is called the location fingerprint
of that point. In the second phase, it analyzes the accu-
racy obtained in the localization process. For this pur-
pose, the developed technique places a significant num-
ber of mobile stations into the area covered by the radio
map and it obtains the vector of received samples from
different APs [7]. The location estimation is made by an
algorithm that computes the distance between the mea-
sured samples and each fingerprint stored in the radio
map. The X and Y coordinates associated with the fin-
gerprint that results in the smallest distance are returned
as the position estimation. Figure 3 shows the relative
delays between the detected rays in a fingerprint and
their contribution to the total field due to the different
ray-tracing effects. Figure 4 shows the power levels
available for all the fingerprints in a regular grid. In both
cases the grid example correspond with 72x72 points
(30x30 meters area size) being 2.4GHz the radiation
frequency of the antenna.
Figure 1. Multipath ray-tracing effects.
Figure 2. Multipath ray-tracing effects.
Figure 3. Relative delays between rays in a fingerprint vs.
electrical field.

A. CORTE-VALIENTE ET AL. 647
Figure 4. Power levels available for all the fingerprints in a
regular grid.
4. Distance Metrics
Distance Metric is the key component used by the fin-
gerprinting technique. By this reason it is important to
explore different similarity measures to find the best dis-
tance metric that minimizes the po sitioning average error.
The method implemented in the localization algorithm is
based on to compute the distance metric between the
vectors of received signals X and the vector of samples
stored in the radio map Y. Then it determines the points
of the grid that corresponds with the position of the mo-
bile stations. The coordinates X and Y that corresponds
with the vector Y that has a smaller distance with the
vector of samples X for a certain position of the mobile
stations are selected as solution. Five equations have
been implemented to explore which will improve more
localization accuracy.
2
1
(, )()
N
Eii
i
Dxyx y


 (1)
1
(, )N
M
ii
i
Dxy xy


 (2)
1
(,) Nii
BC ii
i
x
y
Dxy
x
y



 (3)
2
1
()
(, )Nii
CHI ii
i
x
y
Dxy
x
y



 (4)
'1
(,)( )()( )
Mah
DxyxyCovxxy

  (5)
In the Euclidean metric Equation (1) the mobile
station will be more similar to the fingerprint radio map
if the distance is smaller. More moderate approach
implemented in Manhattan metric Equation (2) is by
using sum of the absolute differences rather than their
squares, as the overall measure of dissimilarity. On the
other hand, in Bray-Curtis and Chi-Squared metrics
Equations (3) and (4) the numerator signifies the differ-
ence and denominator normalizes the difference. In
Mahalanobis metric equation (5) the (x-y)’ term denotes
the (x-y) transpose vector and the Cov term denotes the
covariance matrix, where retrieval performance is sensi-
tive to the sample topology.
5. Interpolation Algorithm
In our next experiment we have implemented an inter-
polation between four fingerprinting weighing based on
its metric distance. For it, the coordinate of the wished
point cannot correspond to the fingerprinting (Figure 5).
The coordinates of the point where it is considered lo-
cating the mobile station, DP, it is determined by means
of the Expression (6), where Nf is the fingerprinting
number, Xj and FP(x,y) are respectively, the value of the
corresponding distance and the coordinate corresponding
to the j fingerprinting. In order to increase the precision
when the mentioned interpolation is applied we made the
weighing with the four fingerprinting that presented the
smaller distance.


1
1
,
(, )
1
Nf
j
j
Nf
j
j
F
Pxy X
DP x y
X









(6)
Figure 5. Location algorithm without interpolation and
with 4 points of interpolation.

A. CORTE-VALIENTE ET AL. 648
In this way we will eliminate those fingerprints that,
due to the great distance to the objective point, present a
higher distance and therefore do not contribute to the
improvement in the accuracy.
6. RF Power vs. Relative Delay Detection
Method
In this case we compare the use of radio frequency (RF)
power levels and relative time delays based on ray-trac-
ing as detection methods to estimate the localization of
set of mobile stations using the fingerprint technique.
The metric considered was the Euclidean distance. The
information provided by the simulation tool is stored in
four vectors. Two of them, Ph and Th, correspond to the
information at every fingerprint. The first vector contains
the power level from the N access points at the finger-
print h and the second one contains the relative delay at
the same point. The Pm and Tm vectors contain the same
information at the mobile station m (Expressions 7 to
10).


123
,,,..., N PhPh PhPhPh (7)


123
,,,..., N ThThThThTh (8)


123
,,,...,
N
PmPm PmPmPm (9)


123
,,,...,
N
TmTmTmTmTm (10)
These vectors are calculated at the beginning of the
process and are stored in a database. The Euclidian dis-
tance between each mobile station and every finger-
printing is calculated using the Expression (11) where
the parameter v is a weighting factor that indicates the
correlation ratio between the powers and delays. This
factor is set to 0 to find the distance by using the power
levels, set to 1 to find the distance by using the relative
delays and set to 0.25 to find the distance with a hybrid
method of the power and delays. The position of the mo-
bile corresponds with the fingerprint whose Euclidean
distance is smaller.

22
1
,(1)()()
N
ii ii
i
DxyPmPhTm Th 




(11)
The number of fingerprints and the frequency are pa-
rameters that would affect the precision of the results.
For this reason the experiment considers two grids: one
consisting of 72x72 fingerprints and another composed
of 36x36, as well as two different frequencies: 2.4GHz
and 5.2GHz. The distance between the fingerprints in the
first and second grids are 40cm and 80cm, respectively.
The simulation also placed 9 AP’s at the above-men-
tioned frequencies and 99 mobile stations randomly dis-
tributed over the grids. Figure 6 shows the area of
28.8x28.8 meters where the simulations have been done.
In order to evaluate the benefits of the detection method
Figure 6. Regular grid example.
Figure 7. Detection methods comparison – Frequency of
2.4GHz.
two statistical indicators have been used. These indica-
tors are the total mean error and the total mean d eviation
(standard deviation). Data obtained after the FASPRI
simulations have been analyzed under MATLAB. Figure
7 shows the results obtained at 2,4GHz and Figure 8 the
results obtained at 5,2GHz. In both graphs the three de-
tection methods analyzed are compared by means of the
statistical indicators. With these results, we can confirm
that the relative delay detection method provides better
results than the power detection method for any grid size
and frequency. The hybrid detection, although it provides
worse results than using delays, can reduce the detection
ambiguity at the cost of increasing the mean error.
However, it should be noted that the mean error is re-
duced when the number of fingerprints is increased for
the same frequency, independent of the detection method
used. In addition, as far as the impact of the frequency
used with the detection method is concerned, we can

A. CORTE-VALIENTE ET AL. 649
observe that, the mean error is lower at 2,4GHz using
power detection; however, it stays constant when using
delay and hybrid detections. Therefore, the grid density
is a more critical factor than the frequency. Table 1
shows the mean error and standard deviation values ob-
tained when comparing the three detection methods. The
two last columns of the table present the percentage of
the mean error that is possible to improve when using
either hybrid versus power detection and delay versus
power detection. Finally, the results obtained have been
analyzed with a statistical point of view. The probability
error was calculated by using the position error of the 99
mobiles. Figures 9, 10 and 11 shows the probability error
distribution for the three methods analyzed in the case of
72x72 grid size for 2.4GHz. It should be noted that the
error distribution function reduces extremely by using
delay detection compared with power or hybrid detection
methods.
7. Distance Metric Comparison and
Interpolation Algorithm Effect
Distance Metric is the key component used by the fin-
gerprinting technique. By this reason, it is important to
Table 1. Mean error and typical deviation detection meth-
ods comparison.
Power
Detection Hybrid Detection Delay Detection
Hybrid
vs.
Power
Delay
vs.
Power
Grid size
and Fre-
quency
Mean error [m]
Typical deviation [m]
Mean error
Improvement
(%)
72x72
2.4GHz 1,9554 0,1871 0,5621 0,0821 0,2504 0,0366 71.28 87.17
72x72
5.2GHz 2,0844 0,1843 0,5207 0,0841 0,2504 0,0366 75.00 87.98
36x36
2.4GHz 1,9801 0,2029 1,1337 0,1610 0,5155 0,0572 32.82 74.24
36x36
5.2GHz 2,5275 0,2548 0,9497 0,1142 0,5155 0,0572 62.69 75.48
Figure 8. Detection methods comparison–frequency of
5.2GHz.
Figure 9. Probability error distribution – power detection.
Figure 10. Probability error distribution – hybrid detection.
Figure 11. Probability error distribution – relative delay
detection.
explore different similarity measures to find the best
distance metric. Five equations have been implemented
to explore which will improve more localization accu-
racy: Euclidean, Manhattan, Bray-Curtis, Chi-Squared
and Mahalanobis distance. In this case the relative delay
detection method was been implemented in the finger-
printing algorithm. Finally an interpolation of the four
best distances has been added. An irregular geometry of

A. CORTE-VALIENTE ET AL. 650
36x36 meters that corresponds with a section of the
polytechnic building has been analyzed (Figure 12). In it,
9 antennas and 5184 fingerprints has been tested being
the frequency of the antenna 2.4 GHz and 100 the
number of mobiles stations to detect.
Running the experiment we are able to find which distance
metric gives best result. For this purpose Matlab tool has
been used. Figure 13 show a detailed comparison of the
accuracy obtained using the five similarity measures,
with and without adding the interpolation algorithm.
Two statistical indicators have been used, the total mean
error and the total mean deviation to evaluate the benefits.
It is clear that conventional distances metrics like Euclid-
ean or Manhattan does not perform the best results. The
average localization error obtained with these metrics is
very similar. Therefore, we can affirm that to calculate
the sum of the absolute differences or their squares in
each fingerprinting iteration process has the same effect.
On the other side, Bray-Curtis and Chi-Squared distances
present better results than the previous metrics du e to the
normalization realized in their expressions. Finally, the
Mahalanobis distance, where the covariance matrix is
sensible to the topology of the radio-map, presents re-
sults slightly better than the rest of metrics, due to the
irregularity of the topology. Similar conclusions are ob-
tained in the case of being applied the technique of in-
terpolation, but being observed, in this case, a reduction
in the two statistical indicators (Table 2).
8. Conclusions
In this work alternative detection methods that can be
used in the fingerprinting technique for mobile
localization has been presented. These methods make
possible the analysis and design of indoor localization
services over WLAN networks. A comparative study
between detection methods based on RF power and
relative delays has firstly been implemented. Secondly,
Figure 12. Irregular section of polytechnic building.
Figure 13. Similarity metrics comparison and interpolation
effect.
Table 2 Mean error [m] - metrics and interpolation com-
parison
Distance Without
Interpolation With Interpolation
Mahalanobis 0.2128 0.2021
Bray-Curtis 0.2253 0.2140
Chi-Squared 0.2303 0.2187
Manhattan 0.2378 0.2259
Euclidean 0.2504 0.2367
we have presented a detailed comparison of five different
similarity metrics to test the performance of the
algorithm. Finally, an interpolation between the finger-
printing weighing based on its distance has been tested.
We can conclude that relative delay detection technique,
which is used in emerging standards such as WiMax
(802.16x), presents better results in the indoor localiza-
tion process than the power detection technique used in
traditional Wi-Fi systems (802.11). On the other side,
conventional distance metrics like Euclidean or Manha-
ttan does not perform necessarily the best accuracy. On
opposite, Mahalanobis distance metric improve the
results when the geometry has irregularities that can been
modeler between measures by the covariance matrix.
Finally, we conclude that the interpolation technique
eliminate those fingerprints that do not contribute to the
improvement in the accuracy.
9. Acknowledgement
This work has been financed by the Community of
Madrid, project S-0505 /TIC/0255, and by the Ministr y of
Education and Science, project TEC-2006-03140.
10. References
[1] Cisco Wireless Location Appliance-Products. Datasheet
2006.

A. CORTE-VALIENTE ET AL. 651
[2] P. Bahl, et al, “Enhancements of the radar user location
and tracking system,” Microsoft Research Technology,
February 2000.
[3] K. Kaemarungsi and P. Krishnamurthy, “Properties of
indoor received signal strength for WLAN location fin-
gerprinting,” Proc. First Annual International Conf. on
Mobile and Ubiquitous Systems: Networking and Ser-
vices, pp. 14–23, August 2004.
[4] F. Sáez de Adana, et al. “Propagation model based on ray
tracing for the design of personal communication systems
in indoor environments,” IEEE Trans. on Vehicular
Technology, Vol. 49, pp. 2105–2112, November 2000.
[5] M. F. Cátedra and J. Pérez-Arriaga, “Cell planning for
wireless communications,” Artech House Publishers,
Boston, 1999.
[6] K. Kaemarungsi, “Distribution of WLAN received signal
strength indication for indoor location determination,”
Proc. First International Symposium on Wireless Perva-
sive Computing, CD-ROM, pp. 6, January 2006.
[7] A. del Corte-Valiente, J. M. Gómez-Pulido, O. Gutiérrez
-Blanco, and M. F. Cátedra-Pérez, “Algoritmos eficientes
de localización en interiores basados en técnicas de
trazado de rayos,” XXIII Simposium Nacional de la
Unión Científica Internacional de Radio (URSI). Madrid
(Spain), September 2008.
[8] A. del Corte-Valiente, J. M. Gómez-Pulido, O. Gutiérrez-
Blanco, and M. F. Cátedra-Pérez, “Efficient Techniques
for indoor localization based on WLAN networks,”
Second International Workshop on User-Centric Techno-
logies and Applications (MADRINET), Salamanca
(Spain), October 2008.