Optics and Photonics Journal, 2011, 1, 130-136
doi:10.4236/opj.2011.13022 Published Online September 2011 (http://www.SciRP.org/journal/opj)
Hybrid Optical Beam-Former in Receiver Mode
Pham Q. Thai, Arokiaswami Alphones
Nanyang Technological University, Singapore City, Singapore
Received July 6, 2011; revised August 10, 2011; accepted August 22, 2011
Abstract
In this paper, an optical beam-former in receiving mode has been proposed and experimentally demonstrated.
The requirement in system’s hardware has been dramatically reduced using a hybrid approach between dis-
persive and non-dispersive delay. The proposed system is capable of supporting RF signals from L-band to
X-band, with large coverage and strong robustness against the grating’s group delay ripples.
Keywords: Chirped Fiber Grating, Group Delay Ripple, Microwave Photonics, Optical Phased Array
Antennas
1. Introduction
Despite having many advantages such as better directivity,
higher gain, and beam-steering, traditional electrical con-
trolled phase array antennas face serious problems
working with large bandwidth RF signals at high fre-
quencies. One of the most difficult obstacles to overcome
is the “beam-squint” phenomenon. The beam direction of
the array changes across the RF signal’s bandwidth. For
applications with large bandwidth and high frequency
requirements, optical beam-forming is a promising can-
didate. Optical beam-formers inherit advantages charac-
teristics such as large bandwidth, compactness, light-
weight, and immunity to electromagnetic interference.
More importantly, they can operate squint-free with wide-
band, high frequency signals, thus avoiding the most
significant drawback of the traditional electrical beam-
formers.
Optical beamformers using chirped grating and optical
delay lines are among the most prominent approaches for
photonic beamforming [1]. However, in the former ap-
proach, the supported array size is limited since each
element requires one tunable laser [2]. In the later ap-
proach, the length of the delay device results in many
obstacles [3]. In order to combine the advantages of both
approaches, optical beamforming systems using a com-
bination of dispersive and non-dispersive delays have
been proposed [4-7]. In [8], we have shown a hybrid
approach between dispersive and non-dispersive delay for
optical beam-former in transmitting mode. The novel
system employing that method has dramatically reduced
hardware requirements.
In this paper, the receiving schematic following our
hybrid approach is presented. In our proposed receiver,
the number of tunable laser is reduced by more than three
times. The number of tunable optical delay line is reduced
by two times. The required time delay for both devices is
also greatly reduced. Experimental and simulation results
have shown that the proposed beam-former can support
signals with wide RF bandwidth from L-band to X-band.
There were only slight distortions in the simulated radia-
tion patterns in comparison with the ideal radiation pat-
terns.
In [9], preliminary simulations and measurements of
the proposed system were reported. In this article, many
more details about the simulation radiation patterns and
measurement results have been disclosed and discussed,
especially about the distortions in radiation patterns. The
system in this article has been improved from the previous
system discussed in [10]. In [10], the combination of
optical signals required intensive fine-tuning to ensure no
interference between signals modulated at the same op-
tical wavelength. In this paper, the problem has been
overcome using polarization beam combiners.
Since the proposed system use chirped grating, the ef-
fect of group delay ripples (GDR) has also been addressed.
As studied in [11,12], the GDR has a strong negative
impact on the performance of optical beam-former using
chirped grating in transmission operation. The study in
[12] also suggested that grating may not be suitable for
receiving operation. However, simulations have shown
that our proposed hybrid system is more robust against
GDR.
The paper is organized as described. The proposed

P. Q. THAI ET AL.131
beam-former is presented in Section 2. Experimental and
simulation results of the proposed system are shown and
discussed in Section 3. Finally, conclusions are drawn in
Section 4.
2. Principles
In order to form the beam toward a particular direction θ
in transmitting operation, an amount of time delay t is
required between two consecutive elements of a phased
array antenna:


sintd c   (1)
where d is the spacing between elements and c is the speed
of light. Because of the additive or destructive combina-
tion of the transmitted signals from the elements, the main
beam in far field would point at the desired direction.
In receiving operations, the above concept is also ap-
plied. It is assumed that the receiving signal approaches at
the angle θ. The delay between the received signals of two
consecutive elements is t. By properly delaying the re-
ceived signal at each element, the beam-former can pro-
vide the strongest accumulated output signal. In a sense,
delaying the received signal can be considered as pointing
the main beam toward the desired direction.
The proposed beam-former in receiving mode is shown
in Figure 1. The signal’s delay at each element is also
noted in that figure. The purpose of the beam-former is to
correctly delay the signals, thus obtaining the strongest
output signal after the photodiode.
The working principle has been discussed in [9]. How-
ever, for better clarity, a brief explanation is provided here.
Firstly, the received signal from each element after the
low noise amplifier is modulated with an optical signal
through an electro-optic modulator. The first and third
laser sources are tunable lasers, while the second and
fourth laser sources are fixed wavelength lasers. The
modulated optical signal for each modulator is noted in
Figure 1.
Couplers are used to combine the modulated signals
into several branches. Optical delay lines are used to delay
the signal as shown in Figure 1. All optical delay lines are
non-dispersive devices. The delay signals from the bran-
ches are then combined and passed through the multi-
Figure 1. Hybrid optical beamformer in receiving mode.

P. Q. THAI ET AL. 132
channel chirped fiber grating (MCFG). The reflectivity
and group delay characteristic of the MCFG can be re-
ferred to in [11]. In a sense, the MCFG can be considered
as a cascade of several nearly identical chirped gratings.
Each optical wavelength falls into one channel of the
MCFG. By tuning the wavelength, λ1 is delayed by 4t in
comparison with λ2, and λ3 is delayed by 2t in comparison
with λ4.
In order to avoid interferences, the optical signals with
the same wavelength have to be of different polarizations.
At the inputs of the polarizing beam splitter (PBS), the
two input signals at the same wavelength are turned or-
thogonal via polarization controllers. The output signal
after the PBS has two polarizations and can still be proc-
essed with the photo detector in the later stage.
As a result, all the input signals have same amount of 7t
delay in time. The accumulated output signal after the
photodiode should be the strongest possible signal. In
other words, by tuning the optical delay lines and the
tunable lasers, the receiver has turned its main beam to-
ward the signal’s incoming direction.
Only four channels of the MCFG are used in this
schematic. Since the MCFG has around 50 channels, it is
possible to increase the supported array size by adding
similar delay branches before the MCFG. In Table 1, the
comparison between hardware’s requirements of the hy-
brid system versus the typical systems is shown.
For optical beamformers using chirped grating, each
element in the array requires one expensive tunable laser,
which makes the system impractical. Optical beamformer
using only optical delay lines is more cost-effective.
However, the long delay requirement causes many dis-
advantages [13].
Our proposed approach, which utilizes a combination
of both chirped grating and optical delay lines, has several
advantages. The hybrid approach has been able to dra-
matically reduce the number of required tunable lasers
and optical delay lines, as seen in Tabl e 1. Moreover, the
required delay for both the grating and delay line is
greatly reduced. The proposed hybrid approach has been
able to subdue the most prominent disadvantages of op-
tical beamformers using chirped grating and optical delay
line.
On the other hand, the scalability of our proposed sys-
tem is limited. In receiving mode, combining modulated
optical signals at the same wavelength may cause inter-
ferences. Polarization controller have been used to ensure
that optical signal at the same wavelength have different
polarization. As a result, each optical carrier signal can
only be used two times. Therefore, although applying the
same concept as in [8], the number of laser sources has to
be increased in receiving operation.
3. Experimental and Simulation Results
In order to test the hybrid system, experiments have been
conducted. Since there were not enough devices, impro-
vising was made. Combining optical signal of different
wavelengths does not distort the signal [14]. With proper
polarizing, combining optical signal of the same wave-
lengths also does not cause distortion [15]. The MCFG
helps prevent beatings [2]. On the other hand, the stability,
precision, linearity, and the supported amount of time
delay are among the most important parameters of a
beamformer. Therefore, the set-up in Figure 2 was used
to measure the delay capability in time domain of the
proposed hybrid optical beamformer scheme. Each
branch of the schematic in Figure 1 was measured at a
time. For the branch with optical delay line, an optical
delay was inserted between the modulator and the MCFG.
In the experiment, the wavelengths for four sources
were 1547.503, 1548.312, 1549.112 and 1549.917 nm,
respectively. The tuning step was 0.001 nm. The optical
signal occupied four separated channels of the MCFG.
The grating was a MCFG from Teraxion, modeled as the
Clear Spectrum DCX D061983.
The photodiode was use to convert the signal back into
electrical domain. The output RF signals were then
compared with the reference input RF signals. The tuning
ranges of the tunable sources were from 1547.373 to
1547.643 nm for the first wavelength and from 1548.982
to 1549.252 nm for the third wavelength. The optical
delay lines were tuned accordingly to the absolute delay
between the wavelengths as explained in the previous
section. The resulting delays between the RF output sig-
nals after the photodiodes at the outputs are shown in
Table 1. Comparison between systems’ requirements in receiving mode.
Number of optical
delay lines
Maximum time delay
from delay line
Number of
tunable lasers
Maximum time delay
from chirped grating
Optical beamformer using chirped grating
(4/8/16 elements) 0/0/0 0/0/0 3/7/15 3t/7t/15t
Optical beamformer using optical delay line
(4/8/16 elements) 3/7/15 3t/7t/15t 0/0/0 0/0/0
Optical beamformer using the hybrid method
(4/8/16 elements) 1/3/7 t/2t/3t 1/2/4 2t/4t/8t

P. Q. THAI ET AL. 133
Figure 2. Experiment setup.
Figures 3 and 4.
As seen in those figures, the time delays are mostly
linear. The results indicate that the tuning devices in the
system, such as the laser sources and the optical lines, can
be programmed to linearly and continuously tune.
The amount of delay stayed mostly unchanged at dif-
ferent RF signal frequencies, as shown in Fi gures 5 and 6.
Considering the optical system as a black box, those re-
sults indicated that the system is able to support signals
for L, S, C, and X-band arrays. The measured group de-
lays of the two set of elements are also nearly the same
since the MCFG channels have similar characteristics.
The results have suggested that the hybrid optical beam-
former system is flexible.
The measured data was imported into Matlab to simu-
late the radiation pattern. The simulated arrays were 8-
element arrays with half-wavelength spacing at 8 GHz
and 2 GHz. Using the measured data, the first array was
able to steer from broadside to 58˚, while the second array
was able to steer from broadside to 17˚. For the 8-element
array, the MCFG is only needed to provide 4t in time
delay. A typical schematic using chirped grating requires
the grating to provide 7t. As a result, given the same
amount of delay from the MCFG, a typical beam-former
using chirped grating can only steer the beam toward 29˚
for 8 GHz RF signals and toward 10˚ for 2 GHz RF signal,
respectively.
In Fi gures 7 and 8, the simulated radiation pattern were
compared with the ideal radiation patterns, where the
there is no GDR and no amplitude fluctuations. The effect
of mutual coupling was calculated in all cases. The time
delay could be fine-tuned to correct the beam direction.
There was less than 0.2˚ and less than 0.5˚ in main beam
direction error for the 2 GHz and 8 GHz arrays, respec-
tively. Both the beam width and the sidelobe level are
affected by the signal’s amplitude. In the system, each
signal passing through one optical delay line suffered 1
dB loss. As a result, the main beam gain was decreased by
1.89 dB, and the sidelobe level was increased by 0.3 dB.
In the worst case with additional amplitude fluctuations
1547.5 1547.521547.54 1547.56 1547.581547.61547.62 1547.641547.66
0
50
100
150
200
250
Wavelength (nm)
Delay (ps)
2nd element
3rd element
4th el em ent
Figure 3. Time delays at the elements in the upper branch.
1548.9515491549.051549.11549.151549.2 1549.251549.3
0
50
100
150
200
250
W a velengt h (nm )
Delay (ps)
2nd el em ent
3rd element
4t h elem ent
Figure 4. Time delays at the elements in the lower branch.
2345678
-40
-30
-20
-10
0
10
20
30
40
50
60
70
RF s i gn al frequency (G Hz )
Delay (ps)
1547. 47 3 nm
1547. 49 3 nm
1547. 51 3 nm
1547. 53 3 nm
Figure 5. Time delay at different frequencies while tuning
the first tunable laser.
from all devices, the main beam gain was decreased by
2.57 dB and the sidelobe level was increased by 0.6 dB.
The simulated pattern’s 3dB beam width is increased by

P. Q. THAI ET AL. 134
2345678
-40
-30
-20
-10
0
10
20
30
40
50
60
70
RF si gnal frequency (GHz )
Delay (ps)
1549.082 nm
1549.103 nm
1549.122 nm
1549.142 nm
Figure 6. Time delay at different frequencies while tuning
the second tunable laser.
-80 -60 -40 -20020 40 60 80
-35
-30
-25
-20
-15
-10
-5
0
5
St eering angle ( D egree)
Gain pattern (dB)
Ideal case
Best case
Worst case
Figure 7. Comparison between the simulated and the ideal
normalized radiation patterns for 8 GHz signals at 55˚.
-80 -60 -40 -20020 40 60 80
-35
-30
-25
-20
-15
-10
-5
0
5
St e ering a ngle (Degr ee)
Gain pattern (dB)
Ideal c ase
Best case
Worst case
Figure 8. Comparison between the simulated and the ideal
normalized radiation patterns for 2 GHz signals at 17˚.
about 0.17˚.
As analyzed in [11,12], the fluctuations in group delay
characteristic of the grating force many limitations on the
optical beamformer using chirped grating. Since the
proposed beamformer uses a chirped grating, its robust-
ness against the GDR error should be tested. The main
beam direction errors of the proposed system were com-
pared with which of a typical optical beamformer using
chirped grating.
In Figure 9, the errors in the hybrid system stay mostly
the same for different array sizes. In comparison, the
errors of the typical system quickly increase. The reason
for that relates to the way the chirped grating is used. In a
typical beamformer, each element is directly controlled
via the delay of the grating, while the hybrid method only
uses two channels of the grating to control the array. The
less dependence on dispersive delay also reduces the
negative effect of the group delay ripples.
In receiving, the quality and the signal’s impulse re-
sponse also have a higher priority. Previous report sug-
gested that optical beamformers using chirped grating do
not perform well in reception [12]. However, the system
in [12] did not use the hybrid approach. The proposed
system, on the other hand, is robust against GDR.
Using the same condition as in [12], linear frequency
modulated (LFM) signals are considered. The details
about LFM can be found in [16]. In short, this particular
type of signal is highly recommended for its resolution
and detection range. The radar systems using those signals
place a strong emphasis on the quality of received signal’s
impulse response [17,18]. The change in the peak’s posi-
tion of the impulse response may cause false distance’s
estimation, while the rise in sidelobe level may conceal
targets.
The fluctuation in group delay causes symmetrical re-
23 4 56 7 8
x 10
9
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
RF ( G Hz)
Mean v al ue of error (degree)
4 elem e nt s
8 elem e nt s
16 elements
4 elem e nt s (hy b ri d)
8 elem e nt s (hy b ri d)
16 elements (hybrid)
Figure 9. Main beam direction error at different RF signal
frequencies and different array sizes.

P. Q. THAI ET AL.135
sponses of the received signal around the non-error signal.
This phenomenon, called “paired echo”, is caused by
dispersion error as studied in [18]. Depending on the
disturbance’s period, the 3 dB width of the main lobe may
increase or new sidelobes may arise in the impulse re-
sponse.
Preliminary study was done in [9]. Further analysis has
shown that the negative effect of GDR is nearly non-
existent. In the hybrid system, only two wavelengths were
tuned across a small region in the grating. Furthermore,
only a part of the total delay was from the grating. As a
result, the influence from GDR was minimized. Although
the echo was presented at several different positions in
time domain, the displacement of them was greatly re-
duced to a few picoseconds, while the LFM pulse duration
is usually in microseconds. Since the scaling is so dis-
tinctive, the negative effects such as distortions from
additive and subtractive combinations are negligible. The
study in [12] also agreed that small ripples do not reduce
the system performance. However, the system in [12]
could not achieve this goal since every element was under
the influence from GDR.
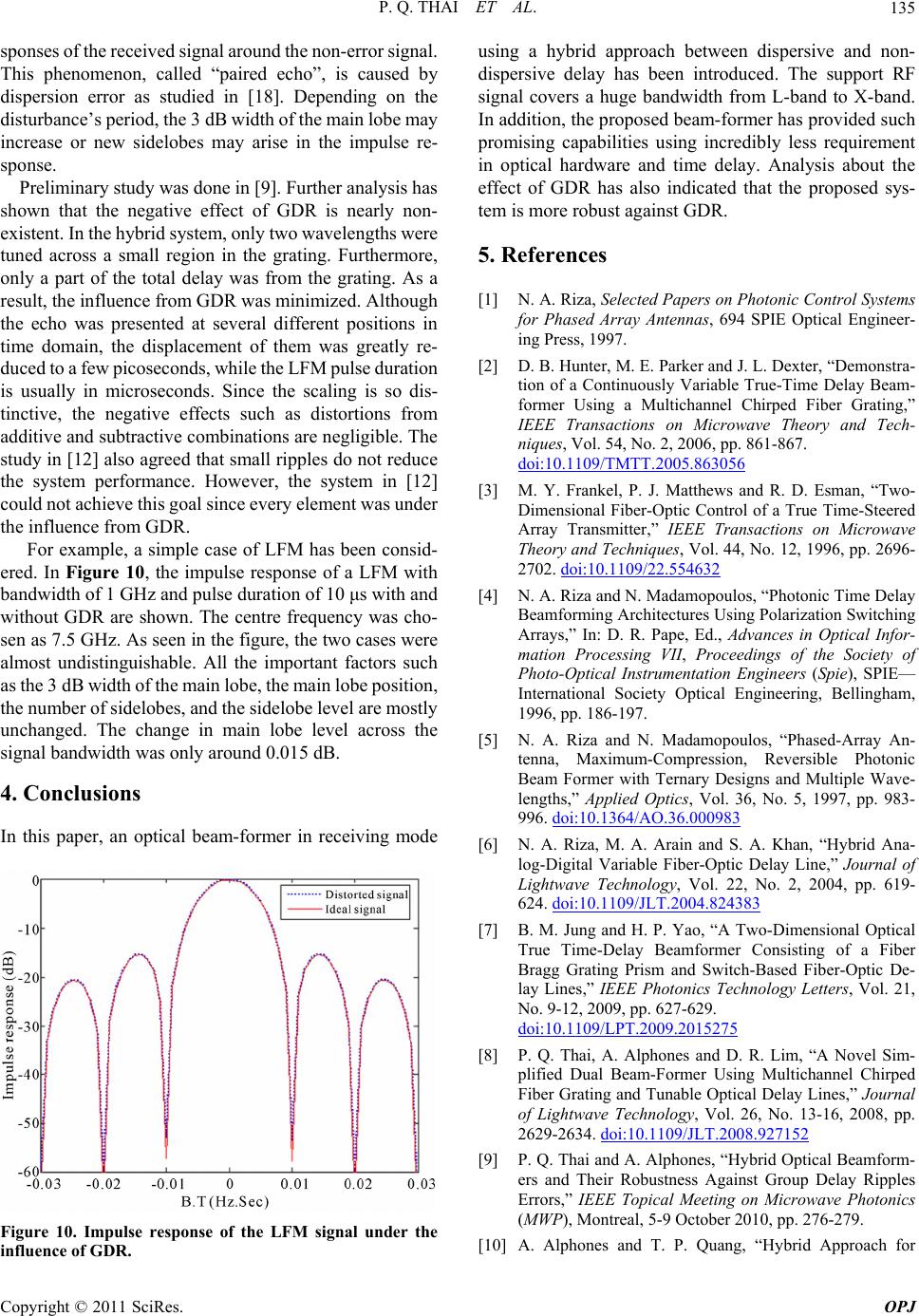
For example, a simple case of LFM has been consid-
ered. In Figure 10, the impulse response of a LFM with
bandwidth of 1 GHz and pulse duration of 10 μs with and
without GDR are shown. The centre frequency was cho-
sen as 7.5 GHz. As seen in the figure, the two cases were
almost undistinguishable. All the important factors such
as the 3 dB width of the main lobe, the main lobe position,
the number of sidelobes, and the sidelobe level are mostly
unchanged. The change in main lobe level across the
signal bandwidth was only around 0.015 dB.
4. Conclusions
In this paper, an optical beam-former in receiving mode
Figure 10. Impulse response of the LFM signal under the
influence of GDR.
using a hybrid approach between dispersive and non-
dispersive delay has been introduced. The support RF
signal covers a huge bandwidth from L-band to X-band.
In addition, the proposed beam-former has provided such
promising capabilities using incredibly less requirement
in optical hardware and time delay. Analysis about the
effect of GDR has also indicated that the proposed sys-
tem is more robust against GDR.
5. References
[1] N. A. Riza, Selected Papers on Photonic Control Systems
for Phased Array Antennas, 694 SPIE Optical Engineer-
ing Press, 1997.
[2] D. B. Hunter, M. E. Parker and J. L. Dexter, “Demonstra-
tion of a Continuously Variable True-Time Delay Beam-
former Using a Multichannel Chirped Fiber Grating,”
IEEE Transactions on Microwave Theory and Tech-
niques, Vol. 54, No. 2, 2006, pp. 861-867.
doi:10.1109/TMTT.2005.863056
[3] M. Y. Frankel, P. J. Matthews and R. D. Esman, “Two-
Dimensional Fiber-Optic Control of a True Time-Steered
Array Transmitter,” IEEE Transactions on Microwave
Theory and Techniques, Vol. 44, No. 12, 1996, pp. 2696-
2702. doi:10.1109/22.554632
[4] N. A. Riza and N. Madamopoulos, “Photonic Time Delay
Beamforming Architectures Using Polarization Switching
Arrays,” In: D. R. Pape, Ed., Advances in Optical Infor-
mation Processing VII, Proceedings of the Society of
Photo-Optical Instrumentation Engineers (Spie), SPIE—
International Society Optical Engineering, Bellingham,
1996, pp. 186-197.
[5] N. A. Riza and N. Madamopoulos, “Phased-Array An-
tenna, Maximum-Compression, Reversible Photonic
Beam Former with Ternary Designs and Multiple Wave-
lengths,” Applied Optics, Vol. 36, No. 5, 1997, pp. 983-
996. doi:10.1364/AO.36.000983
[6] N. A. Riza, M. A. Arain and S. A. Khan, “Hybrid Ana-
log-Digital Variable Fiber-Optic Delay Line,” Journal of
Lightwave Technology, Vol. 22, No. 2, 2004, pp. 619-
624. doi:10.1109/JLT.2004.824383
[7] B. M. Jung and H. P. Yao, “A Two-Dimensional Optical
True Time-Delay Beamformer Consisting of a Fiber
Bragg Grating Prism and Switch-Based Fiber-Optic De-
lay Lines,” IEEE Photonics Technology Letters, Vol. 21,
No. 9-12, 2009, pp. 627-629.
doi:10.1109/LPT.2009.2015275
[8] P. Q. Thai, A. Alphones and D. R. Lim, “A Novel Sim-
plified Dual Beam-Former Using Multichannel Chirped
Fiber Grating and Tunable Optical Delay Lines,” Journal
of Lightwave Technology, Vol. 26, No. 13-16, 2008, pp.
2629-2634. doi:10.1109/JLT.2008.927152
[9] P. Q. Thai and A. Alphones, “Hybrid Optical Beamform-
ers and Their Robustness Against Group Delay Ripples
Errors,” IEEE Topical Meeting on Microwave Photonics
(MWP), Montreal, 5-9 October 2010, pp. 276-279.
[10] A. Alphones and T. P. Quang, “Hybrid Approach for

P. Q. THAI ET AL. 136
Optical Beamforming for Phased Array,” Microwave
Conference Proceedings (APMC), Asia-Pacific 2010,
Singapore City, 7-10 December 2010, pp. 311-317.
[11] P. Q. Thai, A. Alphones and D. R. Lim, “Limitations by
Group Delay Ripple on Optical Beam-Forming With
Chirped Fiber Grating,” Journal of Lightwave Technol-
ogy, Vol. 27, No. 24, 2009, pp. 5619-5625.
doi:10.1109/JLT.2009.2032786
[12] R. Rotman, O. Raz and M. Tur, “Requirements for True
Time Delay Imaging Systems with Photonic Compo-
nents,” IEEE International Symposium on Phased Array
Systems and Technology 2003, New York, 14-17 October
2003, pp. 193-198.
[13] R. Soref, “Optical Dispersion Technique for Time-Delay
Beam Steering,” Applied Optics, Vol. 31, No. 35, 1992,
pp. 7395-7397. doi:10.1364/AO.31.007395
[14] J. Capmany, B. Ortega and D. Pastor, “A Tutorial on
Microwave Photonic Filters,” Journal of Lightwave Tech-
nology, Vol. 24, No. 1, 2006, pp. 201-229.
doi:10.1109/JLT.2005.860478
[15] J. Q. Zhou, S. Aditya, P. Shum, L. Xia and B. P. Parhusip,
“Wide-Range Continuously Tunable Microwave Pho-
Tonic Filter Using High-Birefringence Linearly Chirped
Fiber Bragg Grating and Polarization Beamsplitters,” Op-
tical Engineering, Vol. 48, No. 1, 2009, Article ID:
010502.
[16] M. Skolnik, “Radar Handbook,” 3rd Edition, McGraw-
Hill Professional, Boston, 2008.
[17] A. Kawalec, C. Lesnik, W. Komomiczak, W. Czamecki
and J. Pietrasiniski, “Influence of the Displacement Effect
on Compressed LFM Signal Parameters,” In: C. A. Breb-
bia and G. M. Carlomagno, Eds., Computational Methods
and Experimental Measurements XIII, Wit Transactions
on Modelling and Simulation, 2007, pp. 769-778.
[18] S. Darlington, W. J. Albersheim and A. C. Price, “The
Theory and Design of Chirp Radars,” The Bell System
Technical Journal, Vol. 39, No. 4, 1960, pp. 745-802.