 American Journal of Oper ations Research, 2011, 1, 100-117 doi:10.4236/ajor.2011.13013 Published Online September 2011 (http://www.SciRP.org/journal/ajor) Copyright © 2011 SciRes. AJOR Vertical Decomposition Approach to Solve Single Stage Capacitated Warehouse Location Problem (SSCWLP) Priyanka Verma, Renduchintala Raghavendra Kumar Sharma Department of Industrial and Management Engineering, Indian Institute of Technology, Kanpur, India E-mail: rrks@iitk.ac.in Received May 4, 2011; revised May 25, 2011; accepted June 20, 2011 Abstract Single Stage Capacitated Warehouse Location Problem (SSCWLP) has been attempted by few researchers in the past. These are Geoffrion and Graves [1 ], Sharma [2 ], Sharma [3 ] and Sharma and Berry [4]. In this pa- per we give a “vertical decomposition” approach to solve SSCWLP that uses Lagrangian relaxation. This way SSCWLP is broken into two versions of capacitated plant location problem (the CPLP_L and CPLP_R) by relaxing the flow balance constraints. For CPLP_R, we use well known Lagrangian relaxations given in literature (Christofides and Beasley [5] and Nauss [6]); and adopt them suitably for solving CPLP_L. We show theoretically in this paper that SSCWLP can be more efficiently solved by techniques of vertical de- composition developed in this paper than the method available in literature (Sharma and Berry [4]). Encour- aging computational study is reported in this paper. Keywords: Single Stage Capacitated Warehouse Location Problem, Linear Programming Relaxation, Lagrangian Relaxation, Vertical Decomposition 1. Introduction and Literature Review The problem considered in this work is referred to as the single stage capacitated warehouse location problem (SSCWLP), which arises when the distances between plants and markets are large and it becomes necessary to route the supplies through warehouses (of limited ca- pacities). A set of points are given where warehouses of limited capacities can be located. Each of these points has a known fixed cost associated with them. We are to choose a sufficient number of points where warehouses can be located so that sum tot al of location – distribution co st i s minimized. The study on the SSCWLP is motivated by its applica- tion in many fields, especially in supply chains in which hierarchical structure exists. Melo et al. [7] has reviewed different variants of multistage facility location problem and classified the types of problems attempted in this field on the basis of number of layers, number of location lay- ers, number of commodities, nature of the planning ho- rizon (single/multi period) and the type of data (determi- nistic/stochastic). There are authors who have attempted for SSCWLP and its variants, some of these are discussed here. Geof- frion and Graves [1] gave a Bender’s decomposition ap- proach to solve multi-commodity SSCWLP. Later Hindi and Basta [8] address similar type of distribution design problem with consideration of operating cost per unit of commodity at warehouse along with the fixed cost asso- ciated with it. They used a branch and bound (B&B) al- gorithm based on weak Linear Programming (LP) re- laxation of the problem. Sharma [3] have attempted for a food distribution problem faced by Food Corporation of India (FCI), which is closer to multistage uncapacitated warehouse location problem. Later a solution procedure based on Lagrangian relaxation was developed for this. Klose [9] attempts for capacitated two-stage facility lo- cation problem with single source constraints. The de- veloped model is a single commod ity version of distribu- tion design given by Geoffrion and Graves [1]. They give LP formulation, which is iteratively refined using valid inequalities and facets, and feasible solutions are obtained using simple heuristics by the information from solving LP. In this wa y good lower an d upper boun ds are  P. VERMA ET AL. 101 developed. Tragantalerngsak et al. [10] addresses for two layer facility location problem, where second layer facil- ity has limited cap acity and service of customers is done by only one facility in the second layer. Simultaneously, second layer facility can b e supplied by only one facility in the first layer. A Lagrangian relaxation (LR) based B&B algorithm is given which is compared with LP based B&B and is shown to be efficient as it provide smaller sized tree and requires less CPU time. A realistic variant to the problem that measure custo mer satisfaction is attempted by Eskigun et al. [11] where an outbound supply chain network is designed considering operational dynamics of lead times, etc. They provide a Lagrangian based heuristic, which gives good quality solutions. Me- lachrinoudis et al. [12] uses physical programming ap- proach to reconfigure a warehouse network through consolidation and elimination. Their model enables a decision maker to consider multiple criteria (i.e., cost, customer service, etc) and to express criteria preferences not in a traditional form of weights, but in ranges of dif- ferent degrees of desirability. Farahani and Asgari [13] investigate locating some warehouses in a real-world military logistics system. They use multiple objective decision making techniques to determine the locations of warehouses. To assign each supported center to only one of the located warehouses, a set partitioning model is used. Melachrinoudis and Min [14] develop a mixedin- teger programming model to solve the warehouse redes- ign problem to phase-out underutilized warehouses without deteriorating customer services. They validate the model by applying it to a real-world problem and by its sensitivity analyses. Keskin and Üster [15] attempted for SSCWLP and gave a scatter search-based heuristic approach for the problem. It is to be noted that Geoffrion and Graves [1] and Sharma [2] have attempted the warehouse location prob- lem very interestingly; their formulations are completely different from each other. Formulation given by Sharma [2] has reduced number of variables. Sharma and Berry [4] discuss in detail the differences in the approach to formulation o f SSCWLP due to Geoffrion an d Graves [1] and Sharma [2]. It is to be noted that the primal problem in the Bender’s decomposition used by Geoffrion and Graves [1] and Sharma [2] has a min-cost-flow problem involving flow from plants to warehouse to markets. In this paper, we present a method of “Vertical Decomposi- tion” that breaks the original problem into two pro blems. One involving flow from plants to warehouse (CPLP_L), two involving f l ow from warehouse to ma rket s (C PLP_R ). Using this approach we use the theory developed for capacitated plant location problem (CPLP) (Cornuejols, Sridharan, & Thizy [16] ) (by suita bly extending i t to adopt to new version of CPLP (referred to as CPLP_L)) to solve the original SSCWLP by using a Lagrangian re- laxation. We finally show that this results in a better ap- proach to solve SSCWLP (than the one given by Sharma and Berry [4]). In Section 2 we give the formulation and different re- laxations of SSCWLP. In Section 3 vertical decomposi- tion approach is discussed. Section 4 gives the results of empirical investigation used to verify the theorems of Section 3. In Section 5 we give the detailed procedure to determine lower bounds and feasible solution with the use of these relaxations and the usage of the bounds ob- tained in determination of exact solution to SSCWLP. Section 6 provides computational results along with its analysis. We finally provide our conclusion on this ap- proach in Section 7. 2. Formulation and Relaxations of SSCWLP Here we give a mathematical formulation of SSCWLP using the style of Sharma and Sharma (2000). In later section, different relaxations of SSCWLP are developed and discussed. 2.1. Index i: Index for supply points (plants); i = 1, ···, I; I = number of plants. j: Index for warehouses; j = 1, ···, J; J = number of potential warehouse points. k: Index for markets; k = 1, ···, K; K = number of markets. 2.2. Definition of Constants k D d : Demand for the commodity at ‘k’ k: Demand at market ‘k’ as a fraction of the total market demand; kk k DD i S: Supply available at ‘i’ i : Supply available at point ‘i’ as a fraction of the total market demand; ik k SD . : Fixed cost of locating a warehouse at ‘j’ CAP : Capacity of a warehouse at ‘j’ cap : Capacity of warehouse at ‘j’, as a fraction of the total market demand; k k CAP D . ij cpw : Cost of transporting k quantity of goods from ‘i’ to ‘j’. kD k cwm : Cost of transporting quantity of goods from ‘j’ to ‘k’. k kD 2.3. Definition of Variables ij PW : Quantity shipped from ‘i’ to ‘j’. k WM : Quantity shipped from ‘j’ to ‘k’. Copyright © 2011 SciRes. AJOR  P. VERMA ET AL. Copyright © 2011 SciRes. AJOR 102 ij pw : Quantity shipped from ‘i’ to ‘j’ as a fraction of total market demand; ijij k k pw XPWD : Quantity shipped from ‘j’ to ‘k’ as a fraction of total market demand; kjk k wm k k wm XWMD. y: Location variable (= 1 if warehouse is located at point ‘j’ , 0 otherwise) 2.4. Mathematical Formulation Minimize ijijjkjkj j jk jij cpw xpwcwmxwmfy (1) Subject to: 1 ij ij xpw (2) 1 jk jk xwm (2a) ijj i pwy s,i (3) j kjk wmyd (3a) ,jk ijjj i pwy c ap j (4) kj k j wmycap (4a) j ij i j pw s (5) i kk j wm d (5a) k 0xpw ij 0xwm (6) ,ij jk 0,1y (6a) ,jk j cap y (7) j 1 jj j ij jk (8) ik pw xwm (9) j Just to emphasize that in the above formulati on in s te ad of using single letter names of variable and constant, we use multiple letter names (viz. xpw, xwm, cpw, cwm, etc) so that one can easily recall their meanings, that is, flow/cost between p lant to warehouse (pw) or warehouse to market (wm) etc, while reading the paper. First part of the objective function denotes the total cost of transporting the commod ity from supply poin ts to the warehouses. The second part is the transportation cost from warehouses to markets; and the last part is the fixed cost of locating warehouses. Constraint (2) and (5) are the supply constraint which ensures that the total commodity shipped out from a supply point to all ware- houses can at most be equal to the total supp ly from that supply point. Constraint (2a) and (5a) ensures the total quantity received at any market to be equal to the de- mand at that market. Constraint (3) and (3a) link 0-1 in- teger variables ( y) and other distribution variables that are real and greater than zero. These ensure that if a warehouse is located at any po int then quantities ship ped in or out of that warehouse point are positive, else the quantities shipped will be zero, as the warehouse is not located. Constraint (4) and (4a) ensures that total quan- tity flown in and out of the warehouse does not exceed its capacity if it’s located. We assume to ensure feasibility of the problem. 1 j is Non-negativity constraint on ij pw and k wm are given by (7) and (7a); while (8) is the 0-1 integer con- straint on y. (11) is the flow balance constraint which ensures that total incoming quantity at a particular ware- house from all plants is equal to total outgoing quantity from the same warehouse to all th e markets. (9) is a sur- rogate constraint. With so many constraints available, we can formulate SSCWLP in a variety of different ways. In these if (8) is replaced by (12) we obtain various LP re- laxations. In addition, various relaxations can be ob- tained as Lagrangian relaxation (LR). 2.5. Relaxations of SSCWLP We now develop different LP relaxations and LRs of SSCWLP formulated above. The notation R*_O repre- sent different relaxations of SSCWLP, where (*) is a replacem en t for n u mbers 1 to 4. When integrality restrictions on y are relaxed we obtain (10) 0 i y1 for all j (10) R1_O: (1); Subject to: (2)-(6), (2a)-(6a), (9) and (10). Result 1: R1_O is equal to strong LP relaxation of SSCWLP given by Sharma and Berry (2007). Here re- striction on y is relaxed by (10). Proof: It is easy to see. R2_O: In this LR a constraint introducing upper (U) and lower (P P) limits on the number of open plants is added up. i.e. 1 n j j Py U P (11) This LR is obtained by dualizing (2), (2a), (5) and (5a). Let 0 pw , 0 wm be the Lagrangian multipliers as- sociated with (2), (2a) and i pw , k wm with (5) and 5a) respect i v ely. (  P. VERMA ET AL. 103 00 2_ 00 ,, ,,, 00 max min Oijiijjk xpw xwm y xpwxwmxpw xwmij jk jj iikk ji k kjk cpwxpwxpw xpwcwmxwmxwmxwm fyxpw sxwmdxpwxwm 2 (12) Hence objective (12); Subject to: (3), (3a), (4), (4a), (6), (6a), (7), (9) and (11). R3_O: This is a LR obtained by dualizing (2), (2 a), (6) and (6a). Hence objective is (14); Subject to: (3), (3a), (4), (4a), (6), (6a), (7), (8), (9). R4_O: (1); Subject to: (2)-(6), (2a)-(6a), (7,8) and (9). The original problem SSCWLP is referred for com- parison. 3. Vertical Decomposition Approach for SSCWLP SSCWLP is a well known NP hard problem. Hence, in order to solve large sized and realistic instances of SSCWLP, we devise a decomposition procedure—called “vertical decomposition approach”, which is described below. The objective function (1) may be rewritten as: Minimize 1 ff, where 1,,, 1 min 2 ijij j j ijijj j ij j fxpwcpwyf cpw xpwfy 2,,, 1 min 2 jkjkj j jkjkj j jk j fxwmcwm yf cwmxwmfy This restructured objective function becomes a moti- vation to introduce the vertical decomposition approach for solving SSCWLP. If we give a close look to the for- mulation of SSCWLP, it can be observed that (9) is the only constraint which involves both the flow variables - xpw and xwm. So, if (9) is relaxed, the problem decom- poses into two versions of CPLP, each with one part (f1 or f2) of the objective function shown above. We name this approach as vertical decomposition approach, be- cause the full SSCWLP is decomposed into two parts – left and right. The left part, CPLP_L, contains the vari- ables and parameters of plants and warehouse only (xpw and y). Similarly, the right part, CPLP_R, contains the variables and parameters of warehouse and markets only (xwm and y). Therefore, in a sense, by vertical decompo- sition approach, the stages of the problem are decom- posed to get smaller sized problems, which are relatively easier to solve. Now, (9) has to be relaxed in order to make the SSCWLP formulation amenable to vertical decomposi- tion approach. We use _ low as the Lagrangian multipliers to dualize (11). The resulting formulation of CPLP_L, CPLP_R and SSCWLP, with (9) relaxed, are as shown below: CPLP_L: _, min _ 1 2 CPLP Lijjij xpw yij jj j cpwflowxpw fy (1a) Subject to: (2) , (3), (4), (5), (6), (7), (8) and (9). CPLP_R: _, min _ 1 2 CPLP Rjkjjk xwm yjk jj j cwmflow xwm fy (1b) Subject to: (2a), (3a) , (4a), (5a), (6a), (7), and (8 ). SSCWLP: ,, _ max min_ _ SSCWLPijjij xpw xwm y flow ij kjjk jk j jj cpwflowxpw cwmflowxwmfy or, _ _ max SSCWLPCPLP LCPLP R flow ZZZ _ (1c) Subject to: (2) to (9) and (2a) to (6a). Here the problem SSC WLP is broken int o sub probl ems CPLP_L and CPLP_R. This is vertical decomposition. Sharma [2] decomposed a multi commodity and multi period problem into single commodity and single period problem representing flow from plants to warehouses to markets. This is referred to as horizontal decomposition to bring out the contrast. In the next sub-section different relaxations of CPLP_L and CPLP_R are discussed in detail. Further, procedure to solve SSCWLP using these decomposed problems is discussed. Later a relationship theorem indicating the strength of different relaxations of SSCWLP is given. 3.1. Relaxations of CPLP_L R1_L: (1a); Subject to: (2)-(6) and (10). R 2_L: In this LR is obtained by dualizing (2) and (6). Copyright © 2011 SciRes. AJOR  104 P. VERMA ET AL. 0 2_0 0 , , 1 max min_2 RLijjiijjjii xpw y xpw xpwij ji cpwflowxpwxpwxpwfyxpw sxpw (13) Subject to: (3), (4), (6), (7) and (11). R3_L: (13); Subject to: (3), (4), (6)-(9). R4_L: (1a); Subject to: (2), (3), (4), (5), (6), (7) and (8). The main problem i.e. ZCPLP_L is referred as R4_L for comparison. 3.2. Relaxations of CPLP_R R1_R: (1b); Subject to: (2a)-(6a) and (10). R1_R is a strong LP relaxation (follows from Davis and Ray (1969)). R2_R: LR proposed by Christofides and Beasley [5]. This LR is obtained by dualizing (2a) and (6a). 0 2_ 0 0 , , 1 max min_2 k RRjkjk jkjjkk xwm y xwm xwmjk jk cwmflowxwmxwmxwmfywmdxwm (14) Subject to: (3a), (4a), (6a), (7), (1). R3_R: (14); Subject to: (3a), (4a), (6a), (7), (8). It is attempted by Nauss [6]. R4_R: (1 b); Subject to: (2a), (3a), (4a), (5a), (6a), (7), and (8). The main problem i.e. ZCPLP_R is referred as R4_R for comparison. 3.3. Relationship between Relaxations of CPLP_L Note that CPLP_L is different from CPLP_R. In this section, a comparison of the strength of the bounds given by different relaxations of CPLP_L is given. We con- structed the proofs and found that they are marginally different from CPLP_R (Cornuejols, Sridharan, & Thizy [16]. Theorem 1: 1_ 2_ 3_ 4_ LRLRLR ZZZZ L . This theorem provides the relative effectiven ess of the bounds that may be obtained for these relaxations of CPLP_L. 3.4. Relationship between Relaxations of CPLP_R Cornuejols, Sridharan, & Thizy [16] have given relative strength of different relaxations of standard CPLP which is similar to CPLP_R. Hence, the same relaxations along with their relative strength are used for CPLP_R here in form of theorem 2 below. Theorem 2: 1_ 2_ 3_ 4_ RRRRRR ZZZZ R . This theorem provides the relative effectiven ess of the bounds that may be obta in fo r the se rela xat io ns of C PLP _R. 3.5. Relationship between Relaxations of SSCWLP Here a comparison of the strength of the bounds, given by different relaxations of SSCWLP based on CPLP_L and CPLP_R is given. Proposition 1: The bounds obtained by relaxations R1_O and R2_O are related as 1_ 2_ ORO Proof: With the flow balance constraint (9) relaxed, objective of R2_O can be written as: ZZ. 0 0 2_ 0 ,, ,, ,,_ 000 max min_ _ ROijjiij xpw xwmy xpw xpwij xwm xwmflow jkjkjkjji ikk jk ji k Zcpwflowxpwxpw xpw cwmflowxwmxwmxwmfyxpw sxwmdxpwxwm Subject to: (4) , (4a), (6), (6 a), (7). 0 0 2_ 0 ,, _,, , 000 max maxmin_ _ j ROijji ij xpw xwm y flow xpw xpwij xwm xwm jkjkjkjjiikk jk ji k Zcpwflowxpwxpwxpw cwmflowxwmxwmxwmfyxpw sxwmdxpwxwm Subject to: (4), (4a), (6), (6a), (7). 2_2_ 2_ _ max j ORLR flow ZZZ According to the proofs earlier shown, 1_ 2_ RR ZZ R [for CPLP_R] and 1_ 2_ LR ZZ L [for CPLP_L]. R Hence, 2_1_ 1_ _ max ORLR flow Z R ZZ. Copyright © 2011 SciRes. AJOR  P. VERMA ET AL. 105 Note that here (9) is excluded. If (9) is also included, then the problem become R1_O subjected to its usual constraints. i.e. 1_ 2_ OR ZZO . Proposition 2: 2_3_ ORO Proof: We find that all the results of original problem have identical proof. Hence proof for Proposition 1 has been shown and the proofs for Proposition 2 being simi- lar to it are omitted. When these propositions are com- bined, following theorem is developed showing relative strength of bounds given by different relaxations of SSCWLP. ZZ. Theorem 3: . 1_O2_O3_O4_ORRR R Strongest LP relaxation of SSCWLP proposed by Sharma and Berry [4] is same as relaxation R1_O of SSCWLP proposed. From theorem 3, we observe that the lagrangian relaxations R2_O and R3_O can be better than the strongest relaxations known of SSCWLP (that is R1_O). Empirical study given below shows that differ- ences in performances of relaxations considered in theo- rem 3 are statistically significant. ZZZZ 4. Empirical Investigation for CPLP_L and CPLP_R Here we give results of an empirical study. We find that there is significant difference in the performance of dif- ferent relaxations considered in theorem 3. Sample problems for SSCWLP sized 50 × 50 × 50 were randomly created using C codes; a 50 × 50 × 50 problem corresp onds to a set of 50 pl ants, 50 warehouses and 50 markets. Two categories of problems are consid- ered—nil category (A) and abundance category (B); the same is tabulated in Table 1 belo w. For each of these categories, we created 25 problems in which fixed location cost and the transportation cost are uniformly distributed as shown in Table 1. For each problem instance, we obtained the value of different re- laxations of CPLP_R and CPLP_L using GAMS 22.3 in a Pentium D 2.80 GHz, 1 GB RAM computer. Sub-gra- dient optimization is used for solving Lagrangian relaxa- tions of CPLP_L and CPLP_R. Lagrangian relaxation method is powerful in the sense that it gives good lower bounds (for the minimization problem) in competitive computational time. Starting Lagrangian multiplier is taken either to be 0 or maximum value of 0.5* j capf from all j warehouses. Using trial and error approach between these two choices, good results were obtained. Details can be seen in appendix A. Here we take per- centage improvement between a pair of relaxations (to generate normalized data) for every problem instance; and then t-test is performed. t-tests for bounds of the different relaxations for dif- ferent categories are shown in Tables 2 and 3. These t-values are compared with those in Table 4. Note that each cell of the above table shows the t-value of the t-test between the two relaxations represented by the respective row/column of the matrix. For e.g. t-value between R1 and R2 shows the t-test done between 0 and 100*(R2-R1)/R1. Table 2 shows the t-values obtained for differences in bounds of relaxations for category A problems; and Table 3 is revealing the t-values for dif- ferences in bounds of relaxations for category B prob- lems. 4.1. Analysis for Category A Problems When comparing t values for bounds of different relaxa- tions of CPLP_L [Table 2], the LP relaxation R1_L is giving significantly better bounds as compared to rest all relaxations. We observe from Table 2 that linear relaxa- tion R1_R is the best performing relaxation for category A problems. Table 1. Problem categories for SSCWLP. Parameters Problem category i i j j cap Fixed location cost Transportation Cost A 1.0 1.0 U [100, 1000] U [1, 100] B 5.0 5. 0 U [100-1000] U [1, 100] Table 2. t-test for differences in bounds for category A problems. CPLP_L CPLP_R t-test R1 R2 R3 R4 t-test R1 R2 R3 R4 R1 –23.1+ –23.1+ –0.16 R1 –24.3+ –24.7+ 1.44 R2 1 23.35+ R2 2.2+++ 24.3+ R3 23.35+ R3 24.71+ Copyright © 2011 SciRes. AJOR  106 P. VERMA ET AL. Table 3. t-test for differences in bounds for category B problems. CPLP_L CPLP_R t-test R1 R2 R3 R4 t-test R1 R2 R3 R4 R1 1.01 6.29+ 6.35 R1 –0.61 6.29+ 6.29+ R2 6.29+ 6.35+ R2 6.29+ 6.29+ R3 1.63 R3 3.18+ Table 4. t-critical value (Table value). Significance level α = 0.05 α = 0.01 α = 0.005 t-critical (one tail) 1.68 2.40 2.68 +++: At α = 0.05, significance level = 1 tail; ++: At α = 0.01, significance level = 1 tail; +: At α = 0.005, significance level = 1 tail. 4.2. Analysis for Category B Problems When comparing t-values from Table 3 and Table 4, it is found that most of the relaxations are following theo- rem-1 and theorem-2 respectively for CPLP_L as well as CPLP_R. Significant t-values indicate that the LR R3_L of CPLP_L and R3_R of CPLP_R are providing signifi- cantly better bounds. This results in faster execution of the branch and bound procedure based procedure to solve SSCWLP as shown in the next section. 5. Branch and Bound Procedure to Solve SSCWLP In this section we aim to use three best performing re- laxations to determine bounds in a branch and bound procedure. It is known that stronger the relaxations, bet- ter the bounds, lesser will be the nodes traversed in an enumeration tree and hence one achieves computational advantage. In R2_O and R3_O we relax the flow balance constraints and solve the associated CPLP_R and CPLP_L by lagrangian relaxation procedure. Details of lagrangian relaxation procedure is given in Sharma (1991). The sketch of branch and bound procedure to solve SSCWLP is given below. 5.1. Procedure Branch and Bound Step 1: Initialization. Set current_best _solution = INFIN- ITY; best_lower _bound = - INFINITY; Node [1]. Fixed Var List = {y1 = 0}; Node [1]. Free Var List = {2, ···, N}; Node [2]. Fixed Var List = {y1 = 1}; Node [2]. Free Var List = {2, ···, N}; Add nodes 1 and 2 to list A. Step 2: If list A is empty Then Stop. Optimal Solution Found Else pick up top node (TN) from list A Step 3: Compute lagrangian bound (associated with R2_O or R3_O) or LP relaxation bound (associated with R1_O) associated with node TN (referred to as TN.R_ Bound). If (TN_R_Bound > best_lower_bound), then best_lower_bound = TN_R_Bound . Solve associated min cost flow problem (with TN) and generate a feasible solution for SSCWLP (referred as TN_feasible_solution). If (TN_feasible_solution < cur- rent_best_solution), then current_best_solution = TN_ feasible_solution. If (TN.R_Bound > current_best _solution) Then node TN gets fathomed. Go to step 2. Else If free variables associated with TN >= 1 Then generate two more nodes by setting a chosen free variable associated with TN at 0 and 1; make relevant updates and add these nodes to list A. Else No more branching possible; go to step 2. The above procedure is repeated separately for R1_O, R2_O and R3_O to facilitate a comparison. Empirical investigation is given below. 6. Empirical Investigation for SSCWLP In the earlier sections, the relationship theorem indicat- ing the strength of different relaxations of CPLP_L, CPLP_R and SSCWLP is shown. Also solution proce- dures of some of the best performing relaxations of SSCWLP using vertical decomposition approach are discussed. In this section we focus on usage of these re- laxations of SSCWLP in a branch and bound procedure to obtain an optimal solution. Performance of these re- laxations with its application in a branch and bound is compared with a standard branch and bound procedure (BB) using strong LP relaxation (R1_O) of SSCWLP as its lower bound. We thus compare the new proposed relaxations with that of the best possible known relaxa- tion, R1_O (Sharma and Berry, 2007 ), and show its effi- cacy by the reduction on nodes and time achieved. The objective of this section is to study how well these re- laxations do relative to each other. In particular, we are interested in looking at the influence of supplies versus capacities, capacities versus demands, and fixed costs Copyright © 2011 SciRes. AJOR  P. VERMA ET AL. 107 versus transportations costs on the bounds provided by these relaxations, and the solutions provided by the heu- ristics. Sample problem s for SSC WLP, sized 50 × 50 × 50 and 100 × 100 × 100 (plants × warehouse × markets) were created randomly. From the empirical investigations done for CPLP_L and CPLP_R, we have observed that rela- tionship theorems 1 and 2 are satisfied for the abundance case more promptly. Hence for conducting empirical experiments for complete problem of SSCWLP we have considered varying categories of abundance in supply and capacity limits. Four categories of problems with varying problem size and supply – capacity limits were prepared details of which are given in Table 5. We solved 20 problem instances in each of the category of P1, P2, P3 and P4 on Pentium D 2.80 GHz, 1 GB RAM computer. All the algorithms are coded in MATLAB software with calls to GAMS22.3 for solving the min- cost-flow problem. Details are given in appendix B. We compute percentage improvement for any two methods for every problem instance (to generate normalized data) and then t -tests are perform ed on the numb er of n odes and the time required to solve them; these are shown in Table 6. For each Rm-Rn (“m” and “n” are BB, 1, 2, 3 as shown in column 3 of Table 6), “Nodes” is “t” calculated for the difference between (Number of nodes taken with formu- lation Rm/Number of nodes taken with formulation Rn) and 1. Similarly, “Time” is “t” calculated for difference between CPU time for Rm/CPU time for Rn) and 1. BB refers to the complete enumeration for solving the prob- lem. Nodes under BB refer to th e number of nodes taken to solve the problem. Negative t value indicates reduced number of node and reduced execution time. 6.1. Analysis for Category P1 and P3 Problems Category P1 and P3 problem s have got the same variation in supply and capacity limits, but their problem sizes are different. For th e problem category P1, we note from the Table 6 that the performance (in terms of reduction in number of nodes) of relaxation R1_O is significantly better than BB. Similarly R2_O is significantly better performer as c ompared to R 1_O; however performance of Table 5. Problem categories for SSCWLP. Parameters Problem category Probl e m Size i i j j cap F ixed Location CostTransportation C ost P1 50 × 50 × 50 2.5 2.5 U [100, 1000] U [1, 100] P2 50 × 50 × 50 10 10 U [100, 1 0 00] U [1, 100] P3 100 × 100 × 100 2.5 2.5 U [1500, 2000] U [1, 100] P4 100 × 100 × 100 10 10 U [1500, 2000] U [1, 100] Table 6. t-test for Nodes and time taken to solve the problems. Problem cat egory Problem Size Comparison between ‘Rm-Rn’ Nodes Time R1_O – BB –5.02+ –5.24+ R2_O – R1_O –3.12+ –3.53+ P1 50 × 50 × 50 R3_O – R2_O –2.75+ –1.76+ R1_O – BB –2.67++ –2.92+ R2_O – R1_O –1.32 –1.8+++ P2 50 × 50 × 50 R3_O – R2_O 1 –1.96+++ R1_O – BB –5.07+ –5.1+ R2_O – R1_O –5.56+ –5.72+ P3 100 × 100 × 100 R3_O – R2_O –3.82+ –3.83+ R1_O – BB –2.22+++ –2.47++ R2_O – R1_O –3.83+ –3.82+ P4 100 × 100 × 100 R3_O – R2_O –3.1+ –3.28+ Copyright © 2011 SciRes. AJOR  P. VERMA ET AL. Copyright © 2011 SciRes. AJOR 108 R3_O is still better than R2_O. Also higher t values in- dicate that superiority of R1_O over BB is most signifi- cant and R3_O over R2_O is least (however it is still significant). Exactly similar is the behavior of perform- ance in terms of time taken to solve the problems. That is R3_O is the best performer, superior to R2_O, which is better than R1_O; BB is the worst performer in terms of time. Now when the problem size increases, that is for the problem category P3, it can be observed that R3_O still remains the best performer in terms of reduction in number of n odes as well as time taken to s olve a problem . The relaxations R2_O and R1_O (in that sequence) follow R3_O; however BB still remains the worst performer, both in terms of nodes as well as solution time. Also as can be observed from the t values, the superior perform- ance of R2_O over R1_O is most significant; the pairs “R1_O over BB” and “R3_O over R2_O” follows in that sequence. So it can be inferred from here that the use of relaxation R3_O is most suited to solve small as well as large sized SSCWLP, when there is a moderate level (2.5 times) of over-supply and over-capacity. Solving SSCWLP of category P1 and P3 using Branch and Bound is the least efficient method; however the use of R1_O, R2_O and R3_O (in ascending order of better performance) to de- termine bounds in a Branch and Bound method proves to be very fruitf ul. 6.2. Analysis for Category P2 and P4 problems Category P2 and P4 problem s have got the same variation in supply and capacity limits, but their problem size is different. It can be observed from the Table 6 that for problem category P2, relaxation R1_O performs signifi- cantly better, both in terms of reduction in number of nodes traversed as well as solution time, than the usual branch and bound me thod (BB). However, there is not any significant improvement in the performance of “R2_O over R1_O” or “R3_O over R2_O”. However when the problem size increases, that is for problem category P4, R1_O performs better than BB, R2_O performs better than R1_O, and R3_O performs significantly better than R2_O both in terms of reduction in number of nodes as well as reduction in the time re- quired to solve a problem. Also observing the t values, it is evident that the significant performance of R1_O over BB is not as noteworthy as the significance of “R2_O over R1_O” or “R3_O over R2_O”. So it can be inferre d that when level of over-supply and over-capacity is high (10 times), it is better to solve a smaller sized SSCWLP using R1_O (or R2_O or R3_O) and a large sized SSCWLP using R3_O. Also in this category for smaller sized problems, the use of R1_O, R2_O or R3_O is equally better option compared to the branch and bound method because both R2_O and R3_O perform same as R1_ O. However for large sized p roblems of this category, with the use of relaxations R1_O, R2_O and R3_O (in ascending order of better performance) as bounds in the branch and bound method perform better than the usual branch and bound technique. We have shown that lagrangian based branch and bound procedures (R2_O and R3_O) are superior to R1_O (Sharma and Berry [4]) by implementing these algorithm s on the common platform of MATLAB. It may be noted that BB and R1_O are sol vable by commercially available packages as LINGO, CPLEX or GAMS; whereas la- grangian relaxation based procedures (R2_O and R3_O) are not directly solvable by these commercially available packages . First aut hor of t his paper (a Ph D candida te then) coded these algorithms on MATLAB; and there is enor- mous scope for improvement before its performance be compared to commercially available packages like CPLEX. However it is to be noted that Sharma and Berry [4] showed that R1_o is significantly superior to plain branch and bound procedure (BB) compared on commercially available LINGO software. Thus we provide preliminary evidence that R2_O and R3_O have significant merit for solving SSCWLP. 7. Conclusions The contribution of this work in the existing vast literature of location problems is two folds. First is the introduc- tion of “vertical decomposition” approach for SSCWLP, which can easily be extended to the multi stage ware- house location problems, or to the problems of different domains that are modeled in a manner similar to SSCWLP. Vertical decomposition approach allows us to decompose the complex and large sized SSCWLP into two versions of the standard CPLP. One of the decom- posed problems, CPLP_R, is well researched and has different known relaxations. For the other problem, CPLP_L, we provide different relaxation and show that some of them are similar to CPLP_R. A relationship theorem of different relaxations shows the superiority of some relaxations over the others. In particular we show theoretically that for SSCWLP better Lagrangian relaxa- tion exists than the LP relaxation given by Sharma and Berry [4]. Computational studies give support to our theoretical propositions. Second and the major contribution of this work is to show the efficacy of “vertical decomposition” approach, by using the best performing relaxations of the decom- posed and original SSCWLP to advantageously deter- mine an exact solution to the large sized SSCWLP.  P. VERMA ET AL. 109 Three best performing relaxations are selected based on their relative efficiencies given in relationship theorems, and a procedure to solve them is also provided. These relaxations are used to determine lower bound and a fea- sible solution, which in turn are used in a branch and bound method. Computational study is done for a variety of problems of different sizes. It is found that one of the Lagrangian relaxations (R3_O) is performing best in terms of time and nodes travelled in almost all the cases, as compared to the remaining relaxations. This is a sig- nificant finding as relaxation R1_O was found to be the best performer for SSCWLP by Sharma and Berry [4]; that is we actually landed up finding a relaxation of SSCWLP which is better than that existing in literature. A future research possibility with huge potential could be to extend the results of this paper to multistage location distribution problems, which can be modeled using the “vertical decomposition” approach. 8. References [1] A. M. Geoffrion and G. W. Graves, “Multicommodity Distribution System Design by Benders Decomposition,” Management Science, Vol. 20, No. 5, 1974, pp. 822-844. doi:10.1287/mnsc.20.5.822 [2] R. R. K. Sharma, “Modeling a Fertilizer Distribution Sys- tem,” European Journal of Operational Research, Vol. 51, No. 1, 1991, pp. 24-34. doi:10.1016/0377-2217(91)90142-I [3] R. R. K. Sharma, “Food Grains Distribution in the Indian Context: An Operational Study,” In: A. Tripathi and J. Rosenhead, Eds., Operations Research for Development, New Age International Publishers, New Delhi, 1996, pp. 212-227. [4] R. R. K. Sharma and V. Berry, “Developing New Formu- lations and Relaxations of Single Stage Capacitated Ware- house Location Problem (SSCWLP): Empirical Investi- gation for Assessing Relative Strengths and Computa- tional Effort,” European Journal of Operational Research, Vol. 177, No. 2, 2007, pp. 803-812. doi:10.1016/j.ejor.2005.11.028 [5] N. Christofides and J. E. Beasley, “Extensions to a La- grangean Relaxation Approach for the Capacitated Ware- house Location Problem,” European Journal of Opera- tional Research, Vol. 12, No. 1, 1983, pp. 19-28. doi:10.1016/0377-2217(83)90179-0 [6] R. M. Nauss, “An Improved Algorithm for the Capaci- tated Facility Location Problem,” Journal of Operational Research Society, Vol. 29, No. 12, 1978, pp. 1195-1201. [7] M. T. Melo, S. Nickel and F. Saldanha-da-Gama, “Facil- ity Location and Supplychain Management—A Review,” European Journal of Operational Research, Vol. 196, No. 2, 2009, pp. 401-412. doi:10.1016/j.ejor.2008.05.007 [8] K. S. Hindi and T. Basta, “Computationally Efficient Solution of a Multiproduct, Two-Stage Distribution-Loca- tion Problem,” The Journal of the Operational Research Society, Vol. 45, No. 11, 1994, pp. 1316-1323. [9] A. Klose, “An LP-Based Heuristic for Two-Stage Ca- pacitated Facility Location Problems,” The Journal of the Operational Research Society, Vol. 50, No. 2, 1999, pp. 157-166. [10] S. Tragantalerngsak, J. Holt and M. Rönnqvist, “An Ex- act Method for the Two-Echelon, Single-Source, Capaci- tated Facility Location Problem,” European Journal of Operational Research, Vol. 123, No. 3, 2000, pp. 473-489. doi:10.1016/S0377-2217(99)00105-8 [11] E. Eskigun, R. Uzsoy, P. V. Preckel, G. Beaujon, S. Krishnan and J. D. Tew, “Outbound Supply Chain Net- work Design with Mode Selection, Lead Times and Ca- pacitated Vehicle Distribution Centers,” European Jour- nal of Operational Research, Vol. 165, No. 1, 2005, pp. 182-206. doi:10.1016/j.ejor.2003.11.029 [12] E. Melachrinoudis and H. Min, “Redesigning a Ware- house Network,” European Journal of Operational Re- search, Vol. 176, No. 1, 2007, pp. 210-229. doi:10.1016/j.ejor.2005.04.034 [13] R. Z. Farahani and N. Asgari, “Combination of MCDM and Covering Techniques in a Hierarchical Model for Fa- cility Location: A Case Study,” European Journal of Op- erational Research, Vol. 176, No. 3, 2007, pp. 1839-1858. doi:10.1016/j.ejor.2005.10.039 [14] E. Melachrinoudis, A. Messac and H. Min, “Consolidat- ing a Warehouse Network: A Physical Programming Ap- proach,” International Journal of Production Economics, Vol. 97, No. 1, 2005, pp. 1-17. doi:10.1016/j.ijpe.2004.04.009 [15] B. B. Keskin and H. Üster, “A Scatter Search-Based Heu- ristic to Locate Capacitated Transshipment Points,” Com- puters & Operations Research, Vol. 34, No. 10, 2007, pp. 3112-3125. doi:10.1016/j.cor.2005.11.020 [16] G. Cornuejols, R. Sridharan and J. M. Thizy, “A Com- parison of Heuristics and Relaxations for the Capacitated Plant Location Problem,” European Journal of Opera- tional Research, Vol. 50, No. 3, 1991, pp. 280-297. doi:10.1016/0377-2217(91)90261-S Copyright © 2011 SciRes. AJOR  110 P. VERMA ET AL. Appendix A Computational results for LHSCPLP, category A problem 50 × 50 × 50. R1_LHS R2_LHS R3_LHS R4_LHS S.No Objective Iteration Objective Iteration Objective Iteration Objective Iteration 1 15171.58 2227.00 15169.882 34 15169.885 37 15171.59 59 2 13103.62 1992.00 13102.209 35 13102.21 35 13103.62 81 3 13395.97 2158.00 13393.873 37 13393.874 37 13395.96 65 4 13141.67 1985.00 13139.668 37 13139.672 37 13141.67 78 5 12755.00 2030.00 12753.723 35 12753.727 35 12755 58 6 13424.41 2957.00 13422.896 35 13422.896 35 13424.41 67 7 11782.85 2320.00 11781.386 35 11781.386 35 11782.85 64 8 15200.70 2319.00 15198.726 37 15198.727 37 15200.7 76 9 12873.67 2529.00 12872.091 35 12872.094 35 12873.67 82 10 13231.09 2303.00 13229.122 37 13229.123 37 13231.09 59 11 11347.41 2638.00 11345.71 35 11345.71 35 11347.41 75 12 13626.14 2633.00 13624.432 37 13624.432 35 13626.14 79 13 12858.80 2350.00 12857.204 35 12857.204 35 12858.8 75 14 13592.69 2548.00 13591.355 35 13591.355 35 13592.69 41 15 13970.07 2257.00 13969.255 35 13969.255 35 13970.07 40 16 13348.74 2591.00 13347.718 35 13347.722 35 13348.74 87 17 13164.99 3069.00 13163.302 37 13163.314 35 13164.99 82 18 14130.20 2458.00 14128.861 35 14128.866 35 14130.2 88 19 13469.87 2459.00 13468.141 37 13468.141 37 13469.87 71 20 14493.84 2414.00 14491.808 37 14491.808 37 14493.84 65 21 13842.17 2105.00 13840.31 37 13840.31 37 13842.17 82 22 13700.39 1903.00 13698.911 35 13698.911 35 13700.39 81 23 14183.09 2225.00 14181.863 35 14181.863 35 14183.09 74 24 13956.53 2320.00 13955.301 35 13955.301 35 13956.53 77 25 14220.34 2192.00 14219.027 35 14219.027 35 14220.34 81 Copyright © 2011 SciRes. AJOR  P. VERMA ET AL. 111 Computational results for RHSCPLP, category A problem 50 × 50 × 50. R1_RHS R2_RHS R3_RHS R4_RHS S.No Objective Iteration Objective Iteration Objective Iteration Objective Iteration 1 15172 1022 15170.34 43 15170.34 43 15172 75 2 13104.08 1242 13102.31 43 13102.31 43 13104.08 73 3 13395.2 1180 13393.64 43 13393.65 43 13395.2 59 4 13141.71 1372 13139.67 43 13139.67 43 13141.71 66 5 12754.94 1212 12753.82 41 12753.82 41 12754.94 70 6 13422.99 1047 13421.89 41 13421.89 41 13422.99 66 7 11782.99 793 11781.44 43 11781.44 43 11782.99 56 8 15201.93 1007 15199.67 43 15199.67 43 15201.93 79 9 12873.23 805 12871.22 43 12871.23 43 12873.24 68 10 13230.66 913 13229.05 43 13229.05 43 13230.66 60 11 11346.39 1055 11345.02 41 11345.02 41 11346.39 89 12 13625.79 1259 13623.66 43 13623.66 43 13625.79 77 13 12858.7 966 12857.22 43 12857.22 43 12858.71 55 14 13592.4 1058 13590.74 43 13590.74 43 13592.4 64 15 13971.45 925 13969.87 43 13969.87 43 13971.45 67 16 13348.72 1479 13347.35 41 13347.35 43 13348.72 77 17 13164.36 940 13163.07 41 13163.07 41 13164.36 73 18 14129.75 984 14128.09 43 14128.09 43 14129.75 55 19 13470.62 891 13468.43 43 13468.43 43 13470.62 68 20 14493.33 856 14491.95 43 14491.95 43 14493.33 65 21 13841.5 944 13839.65 43 13839.65 43 13841.5 66 22 13701.3 1438 13699.17 43 13699.17 43 13701.3 54 23 14182.93 908 14181.34 43 14181.34 43 14182.93 65 24 13957.9 985 13955.42 43 13955.43 43 13957.9 74 25 14221.12 1228 14219.6 43 14219.6 43 14221.12 65 Copyright © 2011 SciRes. AJOR  112 P. VERMA ET AL. Computational results for LHSCPLP, category B problem 50 × 50 × 50. R1_LHS R2_LHS R3_LHS R4_LHS S.No Objective Iteration Objective Iteration Objective Iteration Objective Iteration 1 497.088 107 497.088 58 526.801 88 526.8437 282 2 563.076 105 563.076 59 595.003 34 595.0317 92 3 705.075 101 705.067 31 732.775 84 732.8163 330 4 798.315 116 798.32 37 818.037 16 818.0726 12 5 1030.828 107 1030.828 35 1062.68 117 1062.729 267 6 746.658 101 746.658 47 855.058 13 855.1125 541 7 894.089 125 894.089 60 930.367 23 930.4226 129 8 548.966 112 548.966 61 577.275 36 577.3666 74 9 801.892 106 801.892 38 816.326 57 816.3609 45 10 661.608 108 661.61 42 672.059 52 672.1011 13 11 797.476 127 797.476 60 839.853 96 839.9097 316 12 986.781 110 986.781 59 998.737 39 999.0034 141 13 961.018 115 961.018 40 971.421 17 971.4302 75 14 705.189 118 705.187 29 715.545 157 715.6213 246 15 1044.981 118 1044.981 6 1064 4 1068.014 1488 16 775.113 104 775.1 31 827.737 18 827.8167 130 17 513.108 109 513.108 24 514.347 29 514.3696 12 18 1148.365 91 1148.365 37 1168.512 53 1168.53 166 19 516.55 117 516.56 129 573.696 28 573.7134 122 20 808.334 108 808.334 117 839.348 60 839.4315 139 21 684.192 115 684.192 41 701.988 72 702.016 154 22 891.605 111 891.6 76 931.094 111 931.7247 282 23 731.887 112 731.887 44 784.454 28 784.5266 164 24 808.642 129 808.642 51 819.314 67 819.3718 47 25 652.084 115 652.08 23 684.047 24 684.0895 79 Copyright © 2011 SciRes. AJOR  P. VERMA ET AL. 113 Computational results for RHSCPLP, category B problem 50 × 50 × 50. R1_RHS R2_RHS R3_RHS R4_RHS S.No Objective Iteration Objective Iteration Objective Iteration Objective Iteration 1 509.67 2380 509.67 42 538.511 62 538.5373 1062 2 574.659 2468 574.65 74 606.901 73 607.0102 1611 3 719.101 1867 719.105 70 746.441 95 746.4609 1191 4 810.901 2722 810.86 81 830.328 70 830.362 17 5 1042.539 2456 1042.539 70 1074.908 50 1074.91 2037 6 755.642 2859 755.653 86 865.948 90 866.1968 5019 7 906.407 2610 906.4 83 942.529 46 942.5336 599 8 558.779 3002 558.779 81 585.691 77 585.7031 188 9 820.528 2086 820.5 76 833.97 67 833.9829 190 10 673.108 2475 673.076 70 683.48 54 683.486 206 11 805.905 2799 805.9 91 848.007 77 848.0675 892 12 993.454 2457 993.44 90 1005.197 84 1005.206 2672 13 974.165 2377 974.16 83 983.737 73 983.8542 145 14 718.786 1854 718.7 48 728.797 95 728.8193 2267 15 1057.976 2766 1057.96 83 1080.574 53 1080.589 3897 16 786.446 3070 786.44 81 838.286 49 838.2869 906 17 523.433 2614 523.45 80 524.643 61 524.6626 22 18 1157.567 2758 1157.567 83 1177.199 58 1177.203 1171 19 532.823 2395 532.77 78 587.822 69 587.8443 433 20 821.588 2436 821.57 69 854.055 58 854.0678 501 21 696.342 2614 696.342 76 713.355 62 713.3634 1328 22 899.603 2410 899.5 67 939.821 91 939.8355 124 23 744.329 2348 744.319 88 795.562 58 795.5632 2627 24 815.427 3415 815.422 89 827.091 50 827.1029 370 25 669.165 2064 669.16 94 700.632 63 700.6466 182 Copyright © 2011 SciRes. AJOR  114 P. VERMA ET AL. Appendix B Computational results for category P1 problems 50 × 50 × 50. (time in seconds). BB R1 R2 R3 S.No Optimal Nodes Time Nodes Time Nodes Time Nodes Time 1 3628.5500 319 5260 293 4786 269 4513 269 4516 2 4177.1810 137 1741 137 1666 125 1500 125 1525 3 3867.7100 65 909 61 789 57 711 49 706 4 5747.2630 117 1600 111 1525 111 1431 95 1339 5 4077.6970 187 3163 175 2971 175 2873 175 2905 6 3541.6310 69 888 65 811 43 467 43 457 7 5407.8320 109 1571 93 1297 93 1248 93 1436 8 5015.8550 57 662 45 428 45 426 31 382 9 4271.4190 121 1707 119 1598 119 1597 91 1374 10 3725.4900 131 2016 119 1747 119 1743 119 1727 11 4856.1350 211 2105 201 1920 163 1536 139 1372 12 3553.6670 615 7072 519 5883 499 5645 447 5240 13 4115.5330 65 703 45 416 45 409 45 406 14 5218.9520 13 261 13 272 13 264 13 240 15 5413.4630 297 3428 283 3179 271 3030 259 2880 16 4952.1770 167 2192 145 1822 145 1824 145 1830 17 4593.6770 483 5339 359 3879 359 3885 355 3837 18 4983.7330 297 4970 285 4676 235 3844 235 3848 19 4566.5570 364 4893 361 4759 243 3182 243 3202 20 4783.2700 401 4586 329 3682 271 3009 271 3019 Copyright © 2011 SciRes. AJOR  P. VERMA ET AL. 115 Computational results for category P2 problems 50 × 50 × 50. BB R1 R2 R3 S.No Optimal Nodes Time Nodes Time Nodes Time Nodes Time 1 832.7146 33 748 33 742 33 736 33 735 2 656.6308 99 1844 89 1618 89 1622 89 1644 3 375.7824 17 376 13 264 13 264 13 260 4 547.0326 19 646 19 631 19 607 19 599 5 991.5337 57 1297 57 1254 57 1279 57 1254 6 548.5699 65 1594 65 1578 65 1555 65 1572 7 561.4253 23 673 23 675 23 641 23 628 8 670.8930 75 1427 67 1251 67 1259 67 1259 9 547.2954 51 1165 51 1155 51 1132 51 1147 10 632.5004 11 215 7 118 7 98 7 97 11 473.5373 11 219 9 132 9 134 9 129 12 566.0262 11 227 11 219 9 132 9 133 13 583.2800 35 577 35 575 35 574 35 546 14 521.6505 53 1129 53 1110 53 1102 53 1114 15 702.6561 15 310 15 326 15 328 15 270 16 573.2853 13 333 11 266 11 264 11 241 17 940.2433 119 2975 119 2972 119 2968 119 2919 18 572.7860 37 707 37 687 37 688 37 679 19 493.0821 27 855 25 752 25 747 25 743 20 558.8294 57 1421 57 1415 53 1284 53 1306 Copyright © 2011 SciRes. AJOR 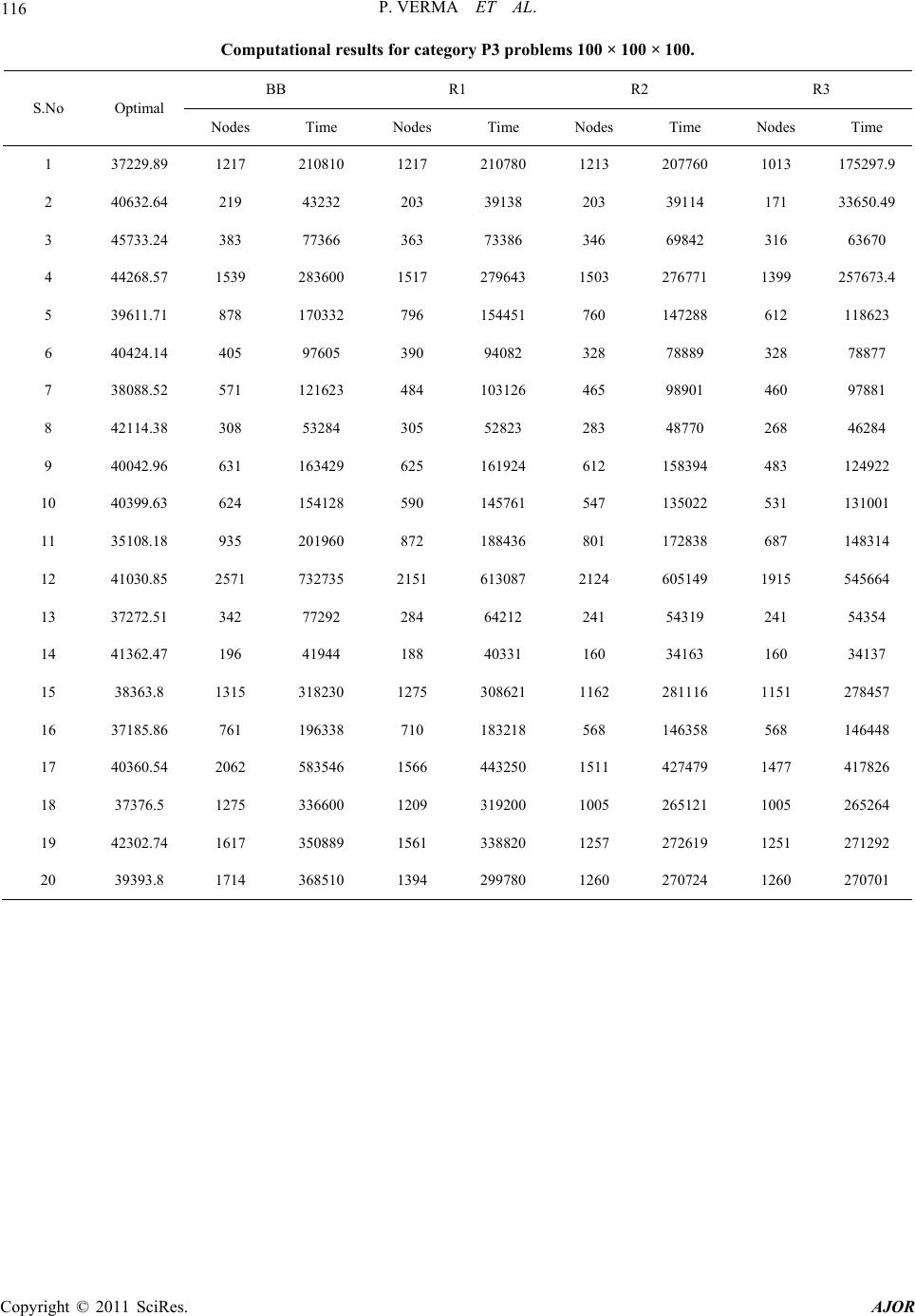 116 P. VERMA ET AL. Computational results for category P3 problems 100 × 100 × 100. BB R1 R2 R3 S.No Optimal Nodes Time Nodes Time Nodes Time Nodes Time 1 37229.89 1217 210810 1217 210780 1213 207760 1013 175297.9 2 40632.64 219 43232 203 39138 203 39114 171 33650.49 3 45733.24 383 77366 363 73386 346 69842 316 63670 4 44268.57 1539 283600 1517 279643 1503 276771 1399 257673.4 5 39611.71 878 170332 796 154451 760 147288 612 118623 6 40424.14 405 97605 390 94082 328 78889 328 78877 7 38088.52 571 121623 484 103126 465 98901 460 97881 8 42114.38 308 53284 305 52823 283 48770 268 46284 9 40042.96 631 163429 625 161924 612 158394 483 124922 10 40399.63 624 154128 590 145761 547 135022 531 131001 11 35108.18 935 201960 872 188436 801 172838 687 148314 12 41030.85 2571 732735 2151 613087 2124 605149 1915 545664 13 37272.51 342 77292 284 64212 241 54319 241 54354 14 41362.47 196 41944 188 40331 160 34163 160 34137 15 38363.8 1315 318230 1275 308621 1162 281116 1151 278457 16 37185.86 761 196338 710 183218 568 146358 568 146448 17 40360.54 2062 583546 1566 443250 1511 427479 1477 417826 18 37376.5 1275 336600 1209 319200 1005 265121 1005 265264 19 42302.74 1617 350889 1561 338820 1257 272619 1251 271292 20 39393.8 1714 368510 1394 299780 1260 270724 1260 270701 Copyright © 2011 SciRes. AJOR  P. VERMA ET AL. Copyright © 2011 SciRes. AJOR 117 Computational results for category P4 problems 100 × 100 × 100. BB R1 R2 R3 S.No Optimal Nodes Time Nodes Time Nodes Time Nodes Time 1 8709.583 425 106250 425 106112 373 93216 373 93210 2 9476.864 25 3995.1 25 3854.1 13 2026.452 13 1985.452 3 9674.657 71 15926 71 15823 71 15888 69 15413.38 4 10010.77 995 267790 995 267725 995 267693 932 250745.5 5 8624.385 189 44226 189 44117 142 33195 142 33151 6 9308.648 414 102672 414 102642 414 102618 384 95187 7 8012.688 370 85840 370 85794 274 63525 274 63526 8 9758.747 988 211432 883 188830 848 181444 786 168167 9 9351.761 587 102725 587 102666 440 76910 440 76904 10 9436.933 1080 190080 1067 187697 1067 187754 986 173438 11 9331.35 119 28203 97 22909 97 22935 97 22942 12 9282.44 1181 232657 1181 232619 934 183966 934 183930 13 7862.446 601 109983 601 109938 590 107879 532 97257 14 9388.992 547 126904 547 126768 547 126812 498 115482 15 9494.626 164 31488 164 31357 139 26636 139 26642 16 9327.953 1144 257400 968 217726 824 185346 824 185317 17 9417.17 1326 290394 1316 288068 1296 283760 1296 283744 18 8126.866 488 89792 481 88445 358 65822 358 65805 19 8095.194 1402 291616 1298 269873 1298 269934 1285 267208 20 9329.764 1205 256665 1202 255878 1094 232970 1094 232993
|