Journal of Biomedical Science and Engineering
Vol.10 No.05(2017), Article ID:76950,9 pages
10.4236/jbise.2017.105B011
The Forward and Inverse Problem Based on Magneto-Acoustic Tomography with Current Injection
Hui Xia1, Guoqiang Liu1, Xin Huang2, Liang Guo2, Yanjiu Yang2, Minhua Lu3
1Department of Engineering Electromagnetics, Applications Institute of Electrical Engineering, Chinese Academy of Sciences, Beijing, China
2University of Chinese Academy of Sciences, Beijing, China
3Guangdong Key Laboratory for Biomedical Measurements and Ultrasound Imaging, Shenzhen, China




Received: April 6, 2017; Accepted: June 13, 2017; Published: June 16, 2017
ABSTRACT
The Magneto-acoustic Tomography with Current Injection (MAT-CI) is a new biological electrical impedance imaging technique that combines Electrical Impedance Tomography (EIT) with Ultrasonic Imaging (UI), which possesses the non-invasive and high-contrast of the EIT and the high-resolu- tion of the UI. The MAT-CI is expected to acquire high quality image and embraces a wide application. Its principle is to put the conductive sample in the Static Magnetic Field(SMF) and inject a time-varying current, during which the SMF and the current interact and generate the Lorentz Force that inspire ultrasonic signal received by the ultrasonic transducers positioned around the sample. And then according to related reconstruction algorithm and ultrasonic signal, electrical conductivity image is obtained. In this paper, a forward problem mathematical model of the MAT-CI has been set up to deduce the theoretical equation of the electromagnetic field and solve the sound source distribution by Green’s function. Secondly, a sound field restoration by Wiener filtering and reconstruction of current density by time-rotating method have deduced the Laplace’s equation that caters to the current density to further acquire the electrical conductivity distribution image of the sample through iteration method. In the end, double-loop coils experiments have been conducted to verify its feasibility.
Keywords:
Magneto-Acoustic Tomography With Current Injection, Axial Symmetry Model, the Forward and Inverse Problem of Electromagnetic Field, Reconstruction Image, Reconstruction Electrical Conductivity Image

1. Introduction
At present, structure imaging is relatively mature in medical imaging for clinical use. However, it is limited to the imaging of the form and structure of the tissue and fails to detect and diagnose tissue lesion in an early stage. A research has shown that a MAT-CI that combined the form and the function of the tissue is expected to fulfill the early warning and diagnosis of a disease. As a new type of imaging method that based on magneto-acoustic coupling, the MAT-CI possesses all the advantages of magneto acoustic coupling and resolves the problem of producing a step signal in magneto acoustic tomography with magnetic induction [1] [2]. The efficiency of energy conversion can be improved by the MAT-CI. Meanwhile exciting coil is not used in the MAT-CI, which leads to negative influence of the altering magnetic field to the current of the specimen and interference of the altering magnetic field to the detection equipments such as ultrasonic transducer.
Towe B C is the first researcher who has conducted the research on the MAT- CI, who put forward a bioelectric currents detecting method through electromagnetic coupling and prove the feasibility of this method through experiment [3]. It was not until 2010 that the Chinese Academy of Medical Sciences and the Institute of Electrical Engineering of the Chinese Academy of Sciences conducted researches on the MAT-CI [4] [5] [6]. This paper conducts systematic research on the theory system of the MAT-CI, focuses on the axial symmetry model, verifies the feasibility in the field of electrical impedance tomography through experimentation and simulation.
2. Research on the Forward Problem of Electromagnetic Field
2.1. Theoretical Analysis on Forward Problem
Assuming the imaging sample’s electrical conductivity is 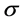 , the sample is put in the static electric field of which the field density is
, the sample is put in the static electric field of which the field density is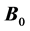 , the current density in the sample after the injunction of the current is
, the current density in the sample after the injunction of the current is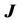 , the electric field intensity in the sample is
, the electric field intensity in the sample is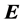 .
.
According to Maxwell’s equations, introduce the magnetic vector potential 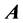 while meet Cullen specification, namely
while meet Cullen specification, namely 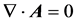
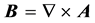 (1)
(1)
From Maxwell’s equation
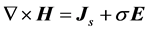 (2)
(2)
Assuming that the permeability of the sample and air are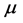 , and simplifying it with the vector equation
, and simplifying it with the vector equation 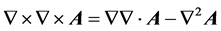 and Cullen specification
and Cullen specification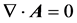 , it is concluded from (1) and (2):
, it is concluded from (1) and (2):
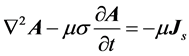 (3)
(3)
Injecting the electric current on the boundary of the sample, and the current density is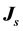 . Using the electric insulation boundary, and the condition of the boundary is
. Using the electric insulation boundary, and the condition of the boundary is
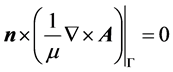
where 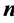 is the normal direction of the outer boundary, where the sample is injected by electric current. With the Equation (3) and boundary condition, magnetic vector potential
is the normal direction of the outer boundary, where the sample is injected by electric current. With the Equation (3) and boundary condition, magnetic vector potential 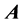 can be obtained and the current density of the specimen can be calculated
can be obtained and the current density of the specimen can be calculated
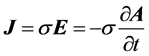 (4)
(4)
2.2. Simulation Analysis on Forward Problem
It is shown in Figure 1 that a hollow cylinder in axial symmetry models is simulated. The electrical conductivity distribution on the inner wall of the cylinder is abnormal. For axial symmetry models, its electrical conductivity distribution of the  section is same. Therefore, in simulation calculation, the parameter distribution of the meridian plane of the dylinder just is researched.
section is same. Therefore, in simulation calculation, the parameter distribution of the meridian plane of the dylinder just is researched.
Assuming that the density of the cylinder is




Lorentz force divergence in this sample

where 

Figure 1. Axial symmetry model and electrical conductivity distribution on meridian plane.

From Equation (4) and (5), Lorentz force divergence on meridian plane of the axial symmetry model can be obtained, as shown in Figure 2. From the Figure 2, it is shown that under the effect of the magneto-static field, the current density and Lorentz force are strong when the electrical conductivity is strong which could motivate stronger Lorentz force divergence sound source. Therefore, there is a corresponding relation between strength of sound source and electrical conductivity distribution.
3. The Inverse Problem of Electromagnetic Field
3.1. Inverse Problem Theory Analysis
In the research of inverse problem on the axisymmetric model, as the current density in the samples is only on the circumferential component

If
Then the current density of the samples will be

The distribution of current density on the meridian plane would be available through the Formula (9). And the distribution of electrical conductivity on the meridian plane of the axisymmetric filed model could be obtained by an iterative method with the result of current density.
3.2. The Simulation Analysis of Inverse Problem
Using the axisymmetric model in Figure 1 and collecting acoustic pressure signal, which the number of is
Reconstruction electrical conductivity distribution is shown in Figure 4, and consistent with Figure 1(b) the original conductivity images, which verifies the feasibility of reconstruction methods.
Figure 2. Lorentz force divergence on forward problem calculation.
Figure 3. Lorentz force divergence reconstructed by the sound pressure.
4. Experiment Study
The experiment principle is shown in Figure 5, the plate that double-ring model in is vertical to the static magnetic field. In order to avoid the reflection between inner ring and outer ring, the plane that fits the inner ring and outer ring, however, the separation between is 2 mm for the probe of ultrasonic transducer is 10 mm. Thus, the double-ring model can be regarded in the same plate when imaging. Figure 5(b) is the top view of double-ring model while point A and B is the injection point electrode, with frequency of 1 KHZ, duty ratio is 0.1%, am- plitude of pulse current is 50 V.
Figure 4. The reconstruction electrical conductivity of sample

Figure 5. Experiment principle of MAT-CI and double-ring model
Magnetic acoustic signal received by ultrasonic transducer as shown in Figure 6, among which CH1 represents waveform of synchronizing signal, CH2 re- presents waveform of excited signal, CH3 represents waveform of magnetic acoustic signal. Each of the vertical axes of CH3 is 5mV while excited signal seen as reference signal. Four peaks in the right side are seen, in accordance with the four positions of electrical conductivity.
Two sets of coaxial double-loop coils are adopted in experiment, the outer diameters of the two sets of coaxial double-loop coils keep the same,


From Figure 8, when the distance between 2 coils becomes 5 mm, the reconstruction image can be reflected the distance clearly, illustrating that MAT-CI
Figure 6. Waveform of magnetic acoustic signal of double-ring model collected by ultrasonic transducer
Figure 7. The image of electrical conductivity of reconstructed double-loop coils. (inner diameter: 10 mm)
experiment system and reconstruction arithmetic can make the resolution of MAT-CI to 5 mm.
5. Conclusion
In this paper, it is conducted systematic research on the theory system of the MAT-CI, focused on the axial symmetry model, and verified the feasibility in the field of electrical impedance tomography through experimentation and simula-
Figure 8. The image of electrical conductivity of reconstruction double- loop coils. (inner diameter: 20 mm)
tion. Meanwhile, by making use of double-loop model to conduct an experiment proving when distance of electrical conductivity becomes 5 mm, the reconstruction image of sample is obtained clearly. It is proved the prospect of MAT-CI in medical area.
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant Nos 51137004, 61427806 and 61271424, and also supported by Instrument development project of Chinese Academy of Sciences Nos YZ201507. Corresponding author E-mail: gqliu@mail.iee.ac.cn.
Cite this paper
Xia, H., Liu, G.Q., Huang, X., Guo, L., Yang, Y.J. and Lu, M.H. (2017) The Forward and Inverse Problem Based on Magneto-Acoustic Tomography with Current Injection. J. Biomedical Science and Engineering, 10, 97-105. https://doi.org/10.4236/jbise.2017.105B011
References
- 1. Xu, Y. and He, B. (2005) Magnetoacoustic Tomography with Magnetic Induction (MAT-MI). Physics in Medicine and Biology, 50, 5175-5187. https://doi.org/10.1088/0031-9155/50/21/015
- 2. Li, X., Xu, Y. and He, B. (2006) Magnetoacoustic Tomography with Magnetic Induction for Imaging Electrical Impedance of Biological Tissue. Journal of Applied Physics, 99. https://doi.org/10.1063/1.2186371
- 3. Wen, H. (1999) Volumetric Hall Effect Tomography—A Feasibility Study Ultrason. Imaging, 21, 186-200. https://doi.org/10.1177/016173469902100303
- 4. Liu, G. Q., He, W. J. and Xia, H. (2010) Research on Forward Problem of Magnetoacoustic Tomography with Magnetic Induction (III)—Sound Field Simulation Method Based on the Sound Source of Divergence of Lorentz Force Optimized with Weak Form. Method Based on Displacement Equation. Modern Scientific Instruments, 1, 17-20.
- 5. Zhang, Y. and Liu, G.Q. et al. (2009) Electromagnatic Forward and Inverse Problems of Non-rotating Magnetoacoustic Tomography with Magnetic Induction. Engineering in Medicine and Biology Society, 2292-2295.
- 6. Liu, G.Q., Huang, X., Xia, H., and Wu, S.Z. (2013) Magnetoacoustic Tomography with Current Injection. Chinese Science Bulletin, 30, 3600-3606. https://doi.org/10.1007/s11434-013-5964-2










