J. Biomedical Science and Engineering, 2011, 4, 631-641 JBiSE
doi:10.4136/jbise.2011.49079 Published Online September 2011 (http://www.SciRP.org/journal/jbise/).
Published Online September 2011 in SciRes. http://www.scirp.org/journal/JBiSE
Mathematical model for steady state current at PPO-modified
micro-cylinder biosensors
Kodhandapani Venu gopal1, Alagu Eswari2, Lakshmanan Rajendran2*
1Department of Mathematics, J.J College of Engineering and Technology, Tiruchirappali, India;
2Department of Mathematics, The Madura College, Madurai, India.
Received 1 July 2011; revised 18 July 2011; accepted 3 August 2011.
ABSTRACT
A Mathemataical model for a modified micro-
cylinder electrode in which polyphenol oxidase ( PPO)
occurs for all values of the concentration of catechol
and o-quinone is analysed. This model is based on
system of reaction-diffusion equations containing a
non-linear term related to Michaelis Menten kinetics
of the enzymatic reaction. Here a new analytical
technique Homotopy Perturbation Method is used to
solve the system of non-linear differential equations.
that describe the diffusion coupled with a Michaelis-
Menten kinetics law. Here we report an analytical
expressions pretaining to the concentration of
catechol and o-quinone and corresponding current in
terms of dimensionless reaction-diffusion parame-
ters in closed form. An excellent agreement with
available limiting case is noticed.
Keywords: Non-Linear Reaction/Diffusion Equation;
Biosensors; Polymer-Modified Micro-Cylinder
Electrode; Polyphenol Oxidase; Homotopy Perturbation
Method
1. INTRODUCTION
Microelectrodes are increasingly being used in biosen-
sors [1-3]. This is due to factors such as fast response
times, high signal: noise ratios and the ability to operate
in low conductivity media, sub-micro volume and in
vivo [4]. The most commonly used microelectrode in
bio-sensor is microcylinder such as carbon fibres. This is
because they are cheap, readily available, their form is
suited to implantation [5] and because much is known
about their surface characteristics [6].
Immobilization of enzymes is used in biosensors to
detect the concentration of a specific analyte as a result
of the biological recognition between the analyte and the
immobilized enzyme. Enzymes have been immobilized
at carbon fibres by many methods. Among all the meth-
ods, layer-by-layer (LbL) self assembly process is a
simple technique which may be applied to a wide range
of enzymes and that it is one of the few immobilization
procedures which allows control over the amount and
spatial distribution of the enzyme [7]. This property is
important both for constructing and modeling studies of
biosensors. The layer-by-layer process was first intro-
duced by Decher and Hong [7]. This method has been
applied to planar electrodes of Au [8,9], carbon elec-
trodes [10] and polystyrene latex [11-15].
To analyse the performance of biosensors of any kind,
it would be useful to have a mathematical model of the
electrode response. Theoretical models of enzyme elec-
trodes give information about the mechanism and kinet-
ics operating in the biosensor. Unlike experimental in-
vestigations of biosensors, where changing one parame-
ter inevitably alters others, the influence of individual
variables can be assessed in an idealized way. Thus, the
information gained from modeling can be useful in sen-
sor design, optimization and prediction of the electrodes
response.
Recently Rijiravanich et al. [16] obtained the steady
state concentration profile of o-quinone and dimen-
sionless sensor response j for the limiting cases of low
substrate concentrations. To the best of our knowledge,
no rigorous analytical solutions for the steady state con-
centrations for micro-cylinder biosensors for all values
of the parameters have been published. In this commu-
nication, we have derived the new and simple analytical
solutions of the concentration and the current for all
values of parameters using the Homotopy Perturbation
Method
2. MATHEMATICAL FORMULATION OF
THE PROBLEM AND ANALYSIS
The system presented here is a cylindrical electrode
which is uniformly coated by an enzyme immobilized in
non-conducting material which is porous to substrate.

K. Venugopal et al. / J. Biomedical Science and Engineering 4 (2011) 631-641 632
The electrode is used in a stirred solution containing an
excess of supporting electrolyte. The enzyme and elec-
trode reaction are [16]:
22
O2catechol2quinone2H Oo (1)
+
quinone 2H2ecatecholo  (2)
Hence the catechol/quinone conversion forms an am-
plification cycle within the enzyme film. While it is pos-
sible in principle to solve for either phenol or catechol as
substrate, solving for catechol is simpler, since it in-
volves only one enzymic conversion. The actual mecha-
nism of that conversion is complex, and involves three
different states, oxy, met, deoxy [17] i.e. (where Ca is
catechol, Q is quinone).
 




1
22 22
deoxy oxy
CuICuI+O2HOHO CuIIOO CuIIHO
k
   
 
(3)
 




2
22 2
oxy met
HOCuIIOO CuIIHOCuIICaCuII2HO 2H
k
   

(4)







3
met deoxy
Cu IICaCuIICu ICu I+
kQ 

(5)
It is assumed that the enzyme concentration is uniform
and that the enzyme reaction follows Michaelis-Menten
kinetics, in which case the reaction in the film is [18]
1
2
112
[]
cat
kk
k
SE ESPE  (6)
where
2
1cat O
kkc and 2
12 3
23
()
O
M
kk kc
Kkk

 (7)
are the rate constant and Michaelis-Menten constant.
The model of a cylindrical electrode modified with both
an enzyme and conducting sites/particles (circles) is
shown in Figure 1. The mass balance for catechol C c
can be written in cylindrical coordinates as follows:
d d0
dd
CCcatEC
CM
Dckcc
r
rrrc K




 (8)
where C c is the concentration profile of catechol,
E
c
is the concentration profile of enzyme, C D and Q D
are its diffusion coefficients, and
M
K
is the Michaelis
constant and Q c is the concentration profile of quinone.
Then the equation of continuum for quinone is generally
expressed in the steady-state by [16]
d
d0
dd
QQ
cat E C
CM
Dc
kcc
r
rrrc K




 (9)
At the electrode surface (0 r) and at the film surface
(1 r) the boundary conditions are given by [16]
*
0
*
1
: , 0
: , 0
CC Q
CC Q
rrc cc
rrccc

 
(10)
where *
C
c is the bulk concentration of catechol scaled
by the partition coefficient of the enzyme film. Adding
the Eqs.8 and 9 and integrating with boundary condition
(10), yields
**
()
() 1
QQ
C
CCC
Dcr
cr
cDc
 (11)
The steady-state current can be given as [16]:

0
0
2πdd
QQ rr
ILr Dcr
nF 
 (12)
We introduce the following set of dimensionless vari-
ables:
*
C
C
c
Cc , *
Q
C
c
Qc ,
0
r
Rr

, *
C
M
c
K
 , 2
0
cat E
E
CM
kcr
DK
 ,
2
0cat E
S
QM
kcr
DK
 , Q
E
CS
D
D


 (13)
where C and Q are the dimensionless concentration
of the catechol and o-quinone. R is the dimensionless
distance parameter. ,
E
S

 and

are the dimen-
sionless reaction-diffusion parameters and saturation
parameter [16].
2
2
d1d 0
d1 d
EC
CC
RR C R




 (14)
2
2
d1d 0
d1 d
SC
QQ
RR C R




 (15)
The boundary conditions are represented as follows:
1 , 0 when 1CQ R

 (16)
10
1 , 0 when CQ Rrr

 (17)
The dimensionless current at the micro-cylinder elec-
trode can be given as follows:

*
1
2πdd
QC R
InFLDcQ R 

 (18)
3. ANALYTICAL SOLUTIONS OF THE
CONCENTRA TIONS AND THE
CURRENT USING THE HOMOTOPY
PERTURBATION METHOD
Nonlinear phenomena play a crucial role in applied

K. Venugopal et al. / J. Biomedical Science and Engineering 4 (2011) 631-641 633
Figure 1. Illustration of the model of a cylindrical electrode
modified with both an enzyme and conducting sites/particles
(circles).
mathematics and chemistry. Construction of particular
exact solutions for these equations remains an important
problem. Finding exact solutions that have a physical,
chemical or biological interpretation is of fundamental
importance. This model is based on steady-state system
of diffusion equations containing a non-linear reaction
term related to Michaelis-Menten kinetics of the enzy-
matic reactions. It is not possible to solve these equa-
tions using standard analytical technique. In the past,
many authors mainly had paid attention to study solution
of nonlinear equations by using various methods, such as
Backlund transformation [19], Darboux transformation
[20], Inverse scattering method [21], Bilinear method
[22], The tanh method [23], Variational iteration method
[24] and Homotopy Perturbation Method [25-28] etc.
The Homotopy Perturbation Method [25-28] has been
extensively worked out over a number of years by nu-
merous authors. The Homotopy Perturbation Method
was first proposed by He [24-26] and was successfully
applied to autonomous ordinary differential equations to
nonlinear polycrystalline solids and other fields.
Recently Meena and Rajendran [29], Anitha et al. [30]
and Manimozhi et al. [31] implemented Homotopy per-
turbation method to give approximate and analytical
solutions of nonlinear reaction-diffusion equations con-
taining a nonlinear term related to Michaelis-Menten
kinetic of the enzymatic reaction. Eswari et al. in series
[32,33] solved the coupled non linear diffusion equations
analytically for the microdisk and micro-cylinder en-
zyme electrode when a product from an immobilized
enzyme reacts with the electrode. Using Homotopy Per-
turbation Method (see Appendix B), we can obtain the
following solutions to the Eqs.14 to 15.

2
1010
1
() 12(1 )
EE E
RrrRrr
CR
 



 








(19)

2
10 10
1
() 2(1 )
SS S
RrrRrr
QR
 



 








(20)
The Eqs.19-20 satisfies the boundary conditions (16)
to (17). These equations represent the new and simple
analytical expression of the concentration of catechol
and o-quinone for all possible values of the parame-
ters E

, S

,

and 10 rr. The Eqs.19 and 20 also
satisfy the relation
() () ()1
ES
CR QR



. From Eqs.19 and 20, we can
obtain the dimensionless current, which is as follows:

10 *12
22(1 )
SS
QC
rr
InFLDc










(21)
Eq. (21) represents the new and closed form of an
analytical expression for the current for all possible val-
ues of parameters.
3.1. Limiting Cases for Unsaturated (First
Order) Catalytic Kinetics
In this case, the catechol concentration C c is less than
Michaelis constant
M
K
. Now the Eqs.8 and 9 reduce to
the following forms:
d
d0
dd
CCcatEC
M
Dckcc
r
rr rK



 (22)
d
d0
dd
QQ
cat E C
M
Dc
kcc
r
rr rK



 (23)
By solving the Eq.22 using the boundary condition
(Eq.10), the concentration of catechol C c can be ob-
tained in the form of modified Bessel functions of zeroth
order 0()
I
r

and 0()
K
r

.
*0000100100
0001 0100
() [()()]() [()()]
() ()() ()()
CC
IrKrKr KrIrIr
crc KrIrKrIr
 
 
  



(24)

K. Venugopal et al. / J. Biomedical Science and Engineering 4 (2011) 631-641 634
where 2
cat ECM
kc DK   (25)
Inserting Eqs.24 into Eqs.11, we can obtain the con-
centration Q
c
0000100100
*
0001 0100
() () [()()]() [()()]
1()()()()
QQ
CC
Dc rIrKrKr KrIrIr
KrIrKrIr Dc
 
 
  




(26)
The sensor response j in terms of modified Bessel function of zeroth order can be obtained as follows:

 
*
0
10010010 0001
0001 0100
2π()()()() ()()
()() ()()
CC
I
jnFLD c
r
K
rI r I rIrK rK r
KrIrKrIr
  
 



(27)
4. COMPARISON WITH LIMITING CASE
WORK OF RIJIRAVANICH ET AL. [16]
Recently, they [16] have derived the analytical expres-
sion of the steady- state concentration Q c (Eq.28 and
sensor response j (Eqs.28 and 29) in integral form for
the limiting case CM
cK

.
11
00 00
0
11 11
*
10
() ln( )
()d ()d()d ()d
ln( )
rr rr
QQ
rr rr
CC
Dc rrr
g
fI rrK rrfIrrK rr
rr Dc
 



 






 (28)

11
00
010 1011
*
10
1
2π ()()()d()d
ln( )
rr
rr
CC
I
jgrfIrKrfIrrKrr
rr
nFLD c
 



 






 (29)
where
0 00000010100
1 [()()], [()()][()()].
g
fIrKrfKrKr IrIr

  
Rijiravanich et al. [16] obtained the empirical expres-
sion of the current
1
2πtanh[(/ 2)(1)]
qp
jx x   (30)
where p and q are empirical constants and 110 .rr


The value of p and q are given for various values of
0
()
x
r

in the Tables 1-3. This empirical expression is
compared our simple closed analytical expression Eq.2 7,
in Tables 2-3. The average relative difference between
our Eq.27 and the empirical expression Eq.30 is 0.71%
when 11.5

 and 0.59% when 15

.
6. DISCUSSION
Figures 2 and 3 shows the dimensionless concentration
profile of catechol ()CR using Eq.19 for all
Table 1. Values of p and qwhich fit Eq.30 to Eq.29
with < 5% error [16].
x
p
q
9.0-7.0 1.00 1.01
6.0-4.0 1.03 1.05
3.0 1.04 1.10
2.0 1.02 1.14a/1.25b
a Valid for 12.0  ; b Valid for 12. 0  
various values of the parameters 10 , , and
SE
rr

 .
Thus it is concluded that there is a simultaneous increase
in the values of the concentration of catechol as well as
in saturated parameter

for small values of
E

. Also
the value of catechol concentration C is approximately
equal to 1 when 1 andR

10 Rrrfor all values of
E
and

 .
Figures 4 and 5 show the concentration profile of
o

quinone ()QR in R space for various values of
and S

 calculated using Eq.20. The plot was con-
structed for 101.5 and 5rr

. From these figures, it is
confirmed that the value of the concentration of o-
quinone increases when 0.1
S

 for small values of

. From the Figures 2-5, we can observed that the di-
mensionless concentration of catechol should vary be-
tween 0 and 1. Because catechol is converted to o

quinone, the o- quinone concentration should be the in-
verse of catechol. The substrate catechol C is mini-
mum and product o-quinone Q is maximum when


10
0.5 2Rrr for all values of and
S

 . The
minimum value of concentration profile of catechol is
2
11
min
88 2
8(1 )
EE E
C





 
 (31)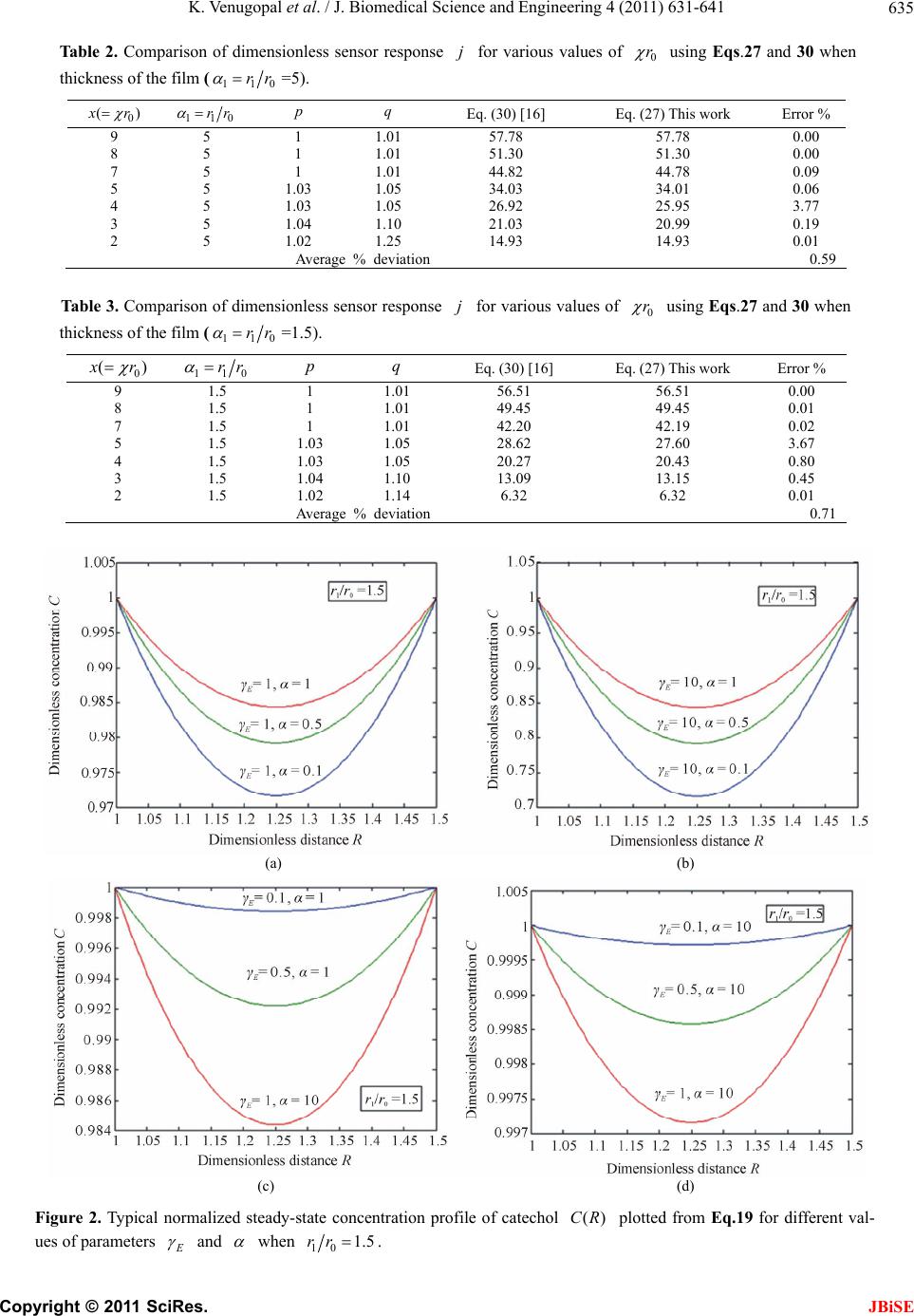

K. Venugopal et al. / J. Biomedical Science and Engineering 4 (2011) 631-641 635
Table 2. Comparison of dimensionless sensor response
j
for various values of 0 r

using Eqs.27 and 30 when
thickness of the film (110
rr  =5).
0
()
x
r

 110 rr  
p
q Eq. (30) [16] Eq. (27) This work Error %
9 5 1 1.01 57.78 57.78 0.00
8 5 1 1.01 51.30 51.30 0.00
7 5 1 1.01 44.82 44.78 0.09
5 5 1.03 1.05 34.03 34.01 0.06
4 5 1.03 1.05 26.92 25.95 3.77
3 5 1.04 1.10 21.03 20.99 0.19
2 5 1.02 1.25 14.93 14.93 0.01
Average % deviation 0.59
Table 3. Comparison of dimensionless sensor response
j
for various values of 0 r

using Eqs.27 and 30 when
thickness of the film (110
rr  =1.5).
0
()
x
r

 110 rr

 p q Eq. (30) [16] Eq. (27) This work Error %
9 1.5 1 1.01 56.51 56.51 0.00
8 1.5 1 1.01 49.45 49.45 0.01
7 1.5 1 1.01 42.20 42.19 0.02
5 1.5 1.03 1.05 28.62 27.60 3.67
4 1.5 1.03 1.05 20.27 20.43 0.80
3 1.5 1.04 1.10 13.09 13.15 0.45
2 1.5 1.02 1.14 6.32 6.32 0.01
Average % deviation 0.71
(a) (b)
(c) (d)
Figure 2. Typical normalized steady-state concentration profile of catechol ()CR plotted from Eq.19 for different val-
ues of parameters
E

and

when 10 1.5rr.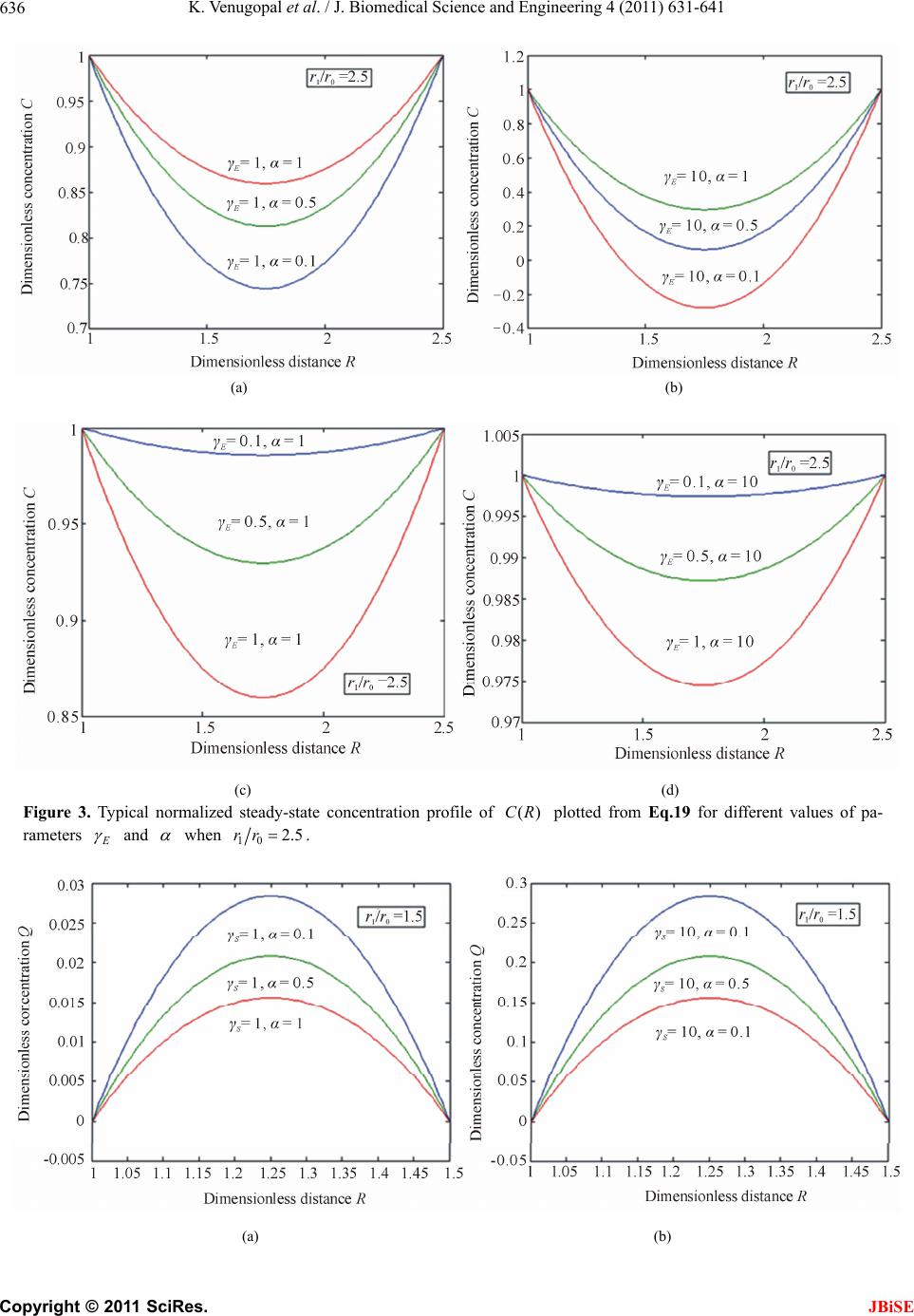

K. Venugopal et al. / J. Biomedical Science and Engineering 4 (2011) 631-641 636
(a) (b)
(c) (d)
Figure 3. Typical normalized steady-state concentration profile of ()CR plotted from Eq.19 for different values of pa-
rameters
E

and

when 102.5rr.
(a) (b)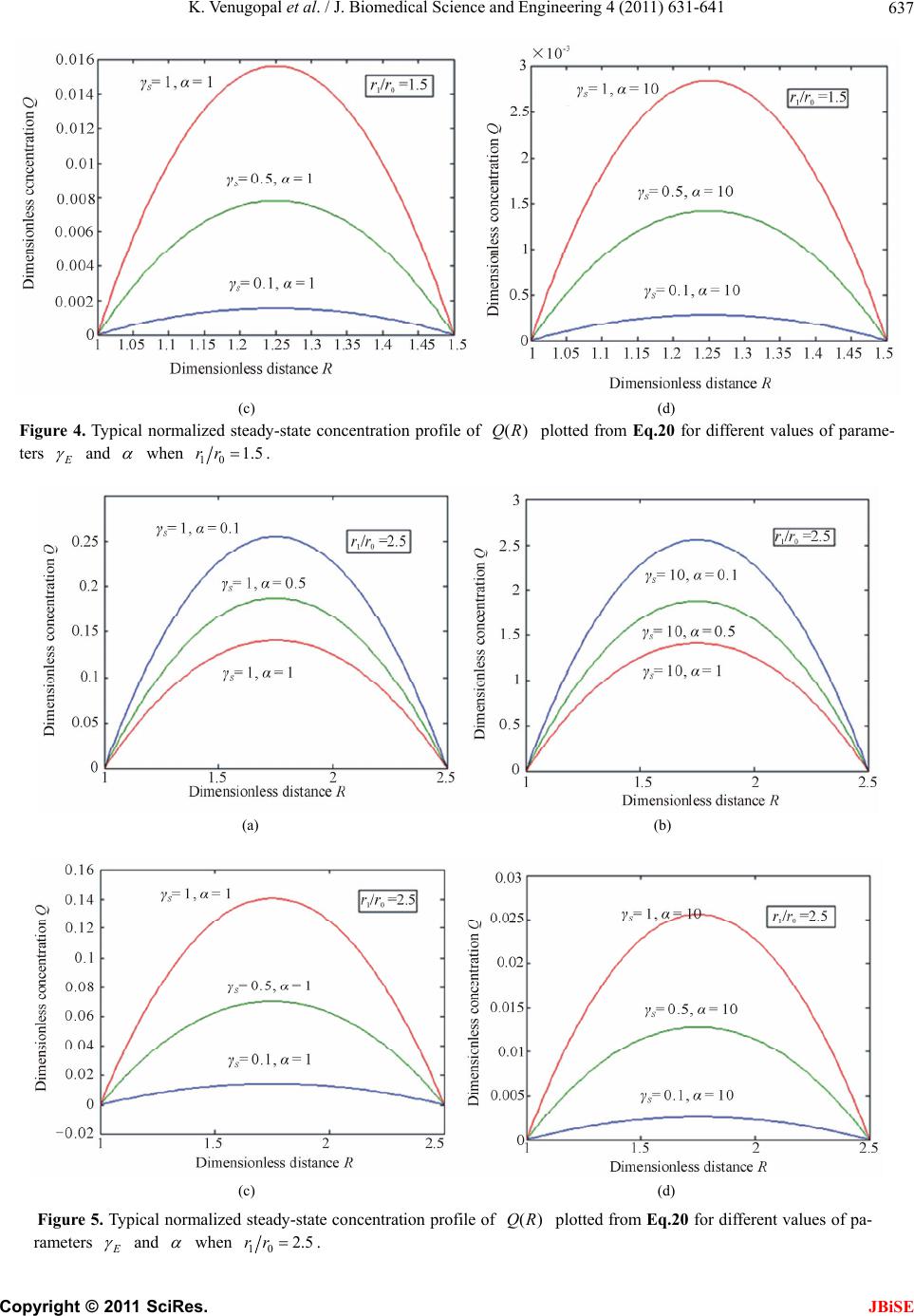

K. Venugopal et al. / J. Biomedical Science and Engineering 4 (2011) 631-641 637
(c) (d)
Figure 4. Typical normalized steady-state concentration profile of ()QR plotted from Eq.20 for different values of parame-
ters
E

and

when 10 1.5rr

.
(a) (b)
(c) (d)
Figure 5. Typical normalized steady-state concentration profile of ()QR plotted from Eq.20 for different values of pa-
rameters
E

and

when 102.5rr.

K. Venugopal et al. / J. Biomedical Science and Engineering 4 (2011) 631-641 638
(a) (b)
Figure 6. Plot of dimensionless current

versus 10 .rr Current is calculated in the Eq.21.
and the maximum value of concentration profile of
quinone is
2
11
max
(1 2)
8(1 )
S
Q




 (32)
where 10 1 rr

. The dimensionless current

versus
10
rr using Eq.21 is plotted in Figure 6. The value of
current

increases when thickness of the film 10 rr
and dimensionless reaction-diffusion parameter S

is
increases or decreases.
7. CONCLUSIONS
A non-linear time independent ordinary differential
equation has been formulated and solved analytically.
Analytical expression for the concentration of catechol
and o-quinone and steady state current are derived by
contains significant non-linear contributions using the
Homotopy Perturbation Method. The primary result of
this work is simple approximate calculation of concen-
tration of catechol, o-quinone and current for all values
of
E

, S

,

and 10 rr and 0 r

. Formerly in
polyphenol oxidase micro-cylinder biosensor models are
[16] have only considered the first order kinetics of the
enzyme and therefore could only be applied to the sen-
sor’s linear range. However, in this paper, calibration
curves of many of the catechol/phenol biosensors con-
tain most important non-linear contributions are reported.
Also, the length of the linear range is an important ana-
lytical parameter. In developing a sensor, experimental
scientists would like this range to cover all concentra-
tions expected in actual samples, as this makes calibra-
tion of the sensor in the field much easier. In Tables 2-3,
our analytical results are compared with limiting case of
first order catalytic kinetics [16] results, which yield a
good agreement with the previous limiting case results.
8. ACKNOWLEDGEMENTS
This work was supported by the Council of Scientific and Industrial
Research (CSIR No.: 01(2442)/10/EMR-II), Government of India. The
authors also thank Mr. M. S. Meenakshisundaram, Secretary, The
Madura College Board, Dr. R. Murali, The Principal,nd S.Thia- gara-
jan, Head of the Department, Madura College, Madurai, India for their
constant encouragement. The authors K. Venugopal and A. Eswari are
very thankful to the Manonmaniam Sundaranar University, Tirunelveli
for allowing to do the research work.
REFERENCES
[1] Revzin, A.F., Sirkar, K., Simonian, A. and Pishko, M.V.
(2002) Glucose, lactate and pyruvate biosensor arrays
based on redox polymer/oxidoreductase nanocomposite
thin films deposited on photolithographically patterned
gold electrodes. Sensor and Actuators B, 81, 359.
doi:10.1016/S0925-4005(01)00982-0
[2] Shi, G., Liu, M., Zhu, M., Zhou, T., Chen, J., Jin, L. and
Jin, J.-Y. (2002) The study of nafion/xanthine oxidase/au
colloid chemically modified biosensor and its application
in the determination of hypoxanthine in myocardial cells
in vivo. Analyst, 127, 396. doi:10.1039/b108462n
[3] Gue, A.-M., Tap, H., Gros, P. and Maury, F. (2002) A
miniaturized silicon based enzymatic biosensor: Towards
a generic structure and technology for multi-analytes as-
says. Sensor and Actuators B, 82, 227.
doi:10.1016/S0925-4005(01)01009-7
[4] Edmonds, T.E. (1985) Electroanalytical application of
carbon fiber electrodes, Analytica Chimica Acta, 175, 1.
doi:10.1016/S0003-2670(00)82713-0
[5] Gonon, F., Suaud-Changny, M.F. and Buda, M. (1992)
Proceedings of satellite symposium on neu-roscience and
technology, Lyon, 215.
[6] Donnet, J.B. and Basal, R.C. (1984) International Fiber
Science and Technology, Carbon Fibers, Dekker, New
York , 3.

K. Venugopal et al. / J. Biomedical Science and Engineering 4 (2011) 631-641 639
[7] Decher, G. and Hong, J.D. (1991) Buildup of ultrathin
multilayer films by a self-assembly process: II. Consecu-
tive adsorption of anionic and cationic bipolar amphi-
philes and polyelectrolytes on charged surfaces. Berichte
der Bunsengesellschaft Für Physikalische Chemie, 95,
1430.
[8] Hodak, J., Etchenique, R., Calvo, E.J., Singhal, K. and
Bartlett, P.N. (1997) Layer by layer self assembly of
glucose oxidase with a poly(allylmanine)-ferrocene re-
dox mediator. Langmuir, 13, 2708.
doi:10.1021/la962014h
[9] Forzani, E.S., Solis, V.M. and Calvo, E.S. (2000) Elec-
trochemical behavior of polyphenol oxidase immobilized
in self-assembled structures layer by layer with cationic
polyallylamine. Analytical Chemistry, 72, 5300.
doi:10.1021/ac0003798
[10] Coche-Guerante, L., Labbe, P. and Mengeand, V. (2001)
Analytical Chemistry, 73, 3206.
doi:10.1021/ac001534l
[11] Lvov, Y. and Caruso, F. (2001) Biocolloids with ordered
urease multilayer shells as enzymatic reactors. Analytical
Chemistry, 73, 4212.
doi:10.1021/ac010118d
[12] Fang, M., Grant, P.S., McShane, M.J., Sukhorukov, G.
B., Golub, V.O. and Lvov, Y. (2002) Magnetic bio/nan-
oreactor with multilayer shells of glucose oxidase and
inorganic nanoparticles. Langmuir, 18, 6338.
doi:10.1021/la025731m
[13] Caruso, F. and Schuler, C. (2000) Enzyme multilayers on
colloid particles: Assembly, stability, and enzymatic ac-
tivity. Langmuir, 16, 9595.
doi:10.1021/la000942h
[14] Caruso, F., Fiedler, H. and Haage, K. (2000) Assembly of
β-glucosidase multilayers on spherical colloidal particles
and their use as active catalyst. Colloids and Surfaces A:
Physicochemical and Engineering Aspects, 169, 287.
doi:10.1016/S0927-7757(00)00443-X
[15] Sun, H. and Hu, N. (2004) 1. Voltammetric studies of
hemoglobin-coated polystyrene latex bead films on py-
rolytic graphite electrodes. Biophysical Chemistry, 110,
297. sdoi:10.1016/j.bpc.2004.03.005
[16] Rijiravanich, P., Aoki, K. and Chen, J., Surareungchai, W.
and Somasundrum, M. (2006) Micro-cylinder biosensors
for phenol and catechol based on layer-by-layer immobi-
lization of tyrosinase on latex particles: Theory and ex-
periment. Journal of Electroanalytical Chemistry, 589,
249-258. doi:10.1016/j.jelechem.2006.02.019
[17] Wilcox, D.E., Porras, A.G., Hwang, Y.T., Lerch, K.,
Winkler, M.E. and Solomon, E.I. (1985) Substrate Ana-
logue Binding to the Coupled Binuclear Copper Active
Site in Tyrosinase. Journal of American Chemical Soci-
ety, 107, 4015. doi:10.1021/ja00299a043
[18] Carbanes, J., Garcia-Canovas, F., Lozano, J.A. and Gar-
cia-Carmona. F (1987) A kinetic study of the melaniza-
tion pathway between L-tyrosine and dopachrome. Bio-
chimica et Biophysica Acta-General Subjects, 923, 187.
[19] Coely, A., et al. (2001) Backlund and darboux transfor-
mation. American Mathematical Society, Providence, RI.
[20] Wadati, M., Sanuki, H. and Konno, K. (1975) Relation-
ships among inverse method, bäcklund transformation
and an infinite number of conservation laws. Progress of
Theoretical Physics, 53, 419.
doi:10.1143/PTP.53.419
[21] Gardener, C.S., Green, J.M., Kruskal, M.D. and Miura,
R.M. (1967) Method for solving the Korteweg–de Vries
equation. Physical Review Letter, 19, 1095.
doi:10.1103/PhysRevLett.19.1095
[22] Hirota, R. (1971) Exact solutions to the equation. de-
scribing cylindrical solitons. Physical Review Letter, 27,
1192. doi:10.1103/PhysRevLett.27.1192
[23] Malfliet, W. (1992) Solitary wave solutions of nonlinear
wave equations. American Journal of Physics, 60, 650.
doi:10.1119/1.17120
[24] He, J.H. (1998) Approximate analytical solution for
seepage flow with fractional derivatives in porous media.
Computer Methods in Applied Mechanics and Engineer-
ing, 167, 57. doi:10.1016/S0045-7825(98)00108-X
[25] He, J.H. (2005) Approximate solution of nonlinear dif-
ferential equations with convolution product nonlineari-
ties. Computer Methods in Applied Mechanics and En-
gineering, 26, 695-700.
[26] He, J.H. (2006) Homotopy perturbation method for solv-
ing boundary value problems. Physical Letter A, 350,
87-88. doi:10.1016/j.physleta.2005.10.005
[27] Ariel, P.D. (2010) Homotopy perturbation method and
the natural convection flow of a third grade fluid through
a circular tube. Nonlinear Science Letters A, 1, 43-52.
[28] Ganji, D.D. and Rafei, M. (2006) Solitary wave solutions
for a generalized hirota-satsuma coupled KdV equation
by homotopy perturbation Method. Physical Letter A,
356, 131-137. doi:10.1016/j.physleta.2006.03.039
[29] Meena, A. and Rajendran, L. (2010) Mathematical mod-
eling of amperometric and potentiometric biosensors and
system of non-linear equations-Homotopy perturbation
approach. Journal of Electroanalytical Chemistry, 644,
50-59. doi:10.1016/j.jelechem.2010.03.027
[30] Anitha, S., Subbiah, A., Rajendran, L. and Ashok K.J.
(2010) Solutions of the coupled reaction and diffusion
equations within polymer-modified ultramicroelectrodes.
Physical Chemistry C, 114, 7030-7037.
[31] Manimozhi, P., Subbiah, A. and Rajendran, L. (2010)
Solution of steady-state substrate concentration in the ac-
tion of biosensor response at mixed enzyme kinetics.
Sensor and Actuators B, 147, 290-297.
doi:10.1016/j.snb.2010.03.008
[32] Eswari, A. and Rajendran, L. (2010) Analytical solution
of steady state current at a microdisk biosensor. Journal
of Electroanalytical Chemistry, 641, 35-44.
doi:10.1016/j.jelechem.2010.01.015
[33] Eswari, A. and Rajendran, L. (2010) Analytical solution
of steady-state current an enzyme-modified microcylin-
der electrodes. Journal of Electroanalytical Chemistry,
648, 36-46. doi:10.1016/j.jelechem.2010.07.002

K. Venugopal et al. / J. Biomedical Science and Engineering 4 (2011) 631-641 640
APPENDIX A
SYMBOLS USED
Symbol Definitions Units
C
D Diffusion coefficient of catechol cm2/s
C
c Concentration profile of catechol mole/cm3
E
c Concentration profile of enzyme mole/cm3
M
K
Michaelis Menten constant mole/cm3
cat
K
Catalytic rate constant sec–1
Q
c Concentration profile of quinone mole/cm3
Q
D Diffusion coefficient of quinone cm2/s
*
C
c Bulk concentration of C mole/cm3
r Radius of the cylinder cm
I Current ampere
0
r Electrode radius cm
1
r Film radius cm
10
rr Dimensionless parameter for film thickness none
0
r

Dimensionless parameter for enzyme kinetic none
j
Dimensionless sensor response none

Dimensionless current none
C Dimensionless concentration of catechol none
Q Dimensionless concentration of quinone none
R
Dimensionless distance none
E

Dimensionless reaction diffusion parameter none
S

Dimensionless reaction diffusion parameter none

Dimensionless saturation parameter none
L
Length of the electrode cm
F
Faraday constant c·mole–1
n Number of electrons none
APPENDIX B
Solution of the Eqs.14 and 15 using Homotopy perturbation method. In this appendix, we indicate how Eqs.19 an d 20
in this paper are derived. Furthermore, a Homotopy was constructed to determine the solution of Eqs.14 and 15.
22
22
dd1
(1 )0
d1 dd
EC
CCdC
pp
RRC RR


 

 

 
(B1)
22
22
dd1d
(1 )0
d1
dd
SC
QQQ
pp
RR C
RR


 

 

 
(B2)
and the initial approximations are as follows:
0, 1, 0 RCQ

 (B3)
1
0
,1, 0
r
RCQ
r


(B4)

K. Venugopal et al. / J. Biomedical Science and Engineering 4 (2011) 631-641 641
The approximate solutions of (B1) and (B2) are
23
01 2 3
CCpC pCpC

 (B5)
and
23
01 2 3
QQpQpQpQ  (B6)
Substituting Eqs.B5 and B6 into Eqs .B1 and B2 and comparing the coefficients of like powers of p
2
00
2
d
: 0
d
C
pR (B7)
2
100 1
2
0
d
d1
: 0
d1
d
E
CC
C
pRR C
R


 
 (B8)
and
2
00
2
d
: 0
d
Q
pR (B9)
2
100
1
2
0
d d1
: 0
d1 d
S
QC Q
pRR C
R


 
 (B10)
Solving the Eqs.B7 to B1 0, and using the boundary conditions (B3) and (B4), we can find the following results
0() 1CR

(B11)




2
10 10
1
1
() 2(1 )
EE E
Rrr rrR
CR
 


 (B12)
and
0() 0QR

(B13)




2
1010
1
1
() 2(1 )
SSS
rr RrrR
QR


 
 (B14)
According to the HPM, we can conclude that
012
1
()lim()
p
CRCRCC C


 (B15)
01 2
1
()lim()
p
QRQRQ QQ


  (B16)
Using Eqs.B11 and (B12) in Eq.B15 and Eqs.B13 and B14 in Eq.B16, we obtain the final results as described in
Eqs.19 and 20.