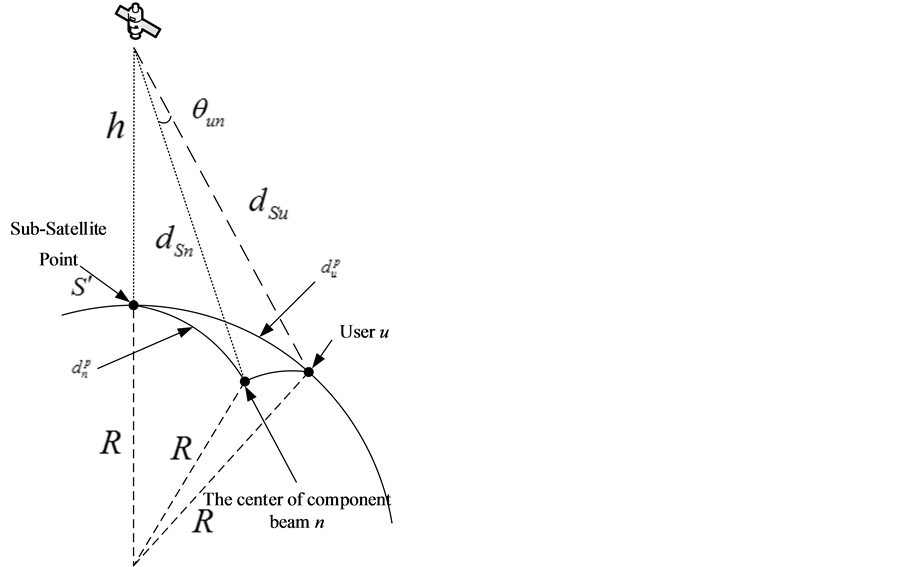International Journal of Communications, Network and System Sciences
Vol.10 No.05(2017), Article ID:76555,11 pages
10.4236/ijcns.2017.105B012
Spatial Correlation Characteristics Analysis of Multi-Beam Channels of Mobile Satellite System
Ziming Su, Xiang Fei, Yuxin Cheng, Jianjun Wu*
Institute of Advanced Communications, EECS, Peking University, Beijing, China




Received: March 20, 2017; Accepted: May 23, 2017; Published: May 26, 2017
ABSTRACT
Due to the influence of scatterers around the receiving antenna, the multipath signal in satellite mobile communication systems is correlated with each other which would influence the system performance. There is no systematic standard on the channel modelling of the wideband satellite channel at present, so the study of the modelling of the wideband satellite channel is of great importance. In this paper, firstly we created a multi-beam model which can figure out the antenna gain of the nth component beam. Secondly, we combined the characteristics of multi-beam satellite channel and the distribution of the scatterers, and set up a three-dimension random channel model. This model is more realistic for satellite communication system since it considers the height of scatterers. According to the channel models, we had the formula of spatial correlation coefficient. We used the formula to calculate the relationship between spatial correlation coefficient and the interval of antennas. The result shows that the spatial correlation exists and cannot be ignored while modeling for mobile satellite system.
Keywords:
Satellite MIMO, Spatial Correlation, Multi-Beam, Scatterers, Channel Model

1. Introduction
The development of wideband multimedia service has raised demand of speed and spectrum efficiency of a new generation mobile-satellite communication system. In the condition of limitation of power, it is significant to make use of space resource to increase system performance. Under the influence of the distribution of scatterer near the receiver antenna, channel fading has spatial correlation in mobile-satellite communication system.
Compatible with LTE standard will be a trend for the new generation of mobile-satellite communication system. Because multiple-input multiple-output (MIMO) is an important part of LTE standard, the research of channel spatial correlation has certain reference value.
Currently, the commonly used classical satellite channel models are Loo model, Lutz model, Fontan model etc.
In terms of research regarding channel spatial correlation characteristics, a spatial Rayleigh-fading correlation model for MIMO has been proposed in [1]. This model assumes uniform distribution of the scatterers with respect to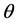 , the angle-of-arrival (AOA) at the subscriber unit. The model also assumes that all received rays are equal in power, which is not a realistic assumption for multipath environments. An extension of this model for Rician-fading channels appeared in [2], which assumes von Mises angular distribution for scatterers.
, the angle-of-arrival (AOA) at the subscriber unit. The model also assumes that all received rays are equal in power, which is not a realistic assumption for multipath environments. An extension of this model for Rician-fading channels appeared in [2], which assumes von Mises angular distribution for scatterers.
Moreover, Mahmoud developed a geometrical based hyperbolic channel (GBHC) model for macrocells in [3]. A combination of the model in [3] and scalar stochastic fading model for local scatterers was presented in [4]. The GBHC model is a two-dimension model, which assumed that the scatterers are arranged circularly around the mobile station (MS), and the distances between the MS and scatterers are subject statistically to a hyperbolic distribution.
This paper mainly researches spatial correlation of multi-beam channels of mobile satellite system. Different from current spatial correlation research, we create a three-dimension channel model based on stochastic geometric model, which considers the height of scatterers, and deducts spatial correlation coefficient among channels with numeric calculation and analysis.
2. Satellite Channel Model
2.1. Multi-Beam Model
Satellite multiple beam antenna (MBA) began to develop in the 1970s to 1980s. Single Feed per Beam (SFB) technology was adopted in the early stage. Later, multiple feeds per beam (MFB) technology was employed. Compared with phased-array antenna, feed beam of MBA is more narrow, and stronger. So the MBA has been widely used in satellite mobile communication systems in 1990s.
According to the structure, MBA can be divided to three categories: phased array antenna, reflector antenna and lens antenna. In this paper, we use reflector antenna to create multi-beam model.
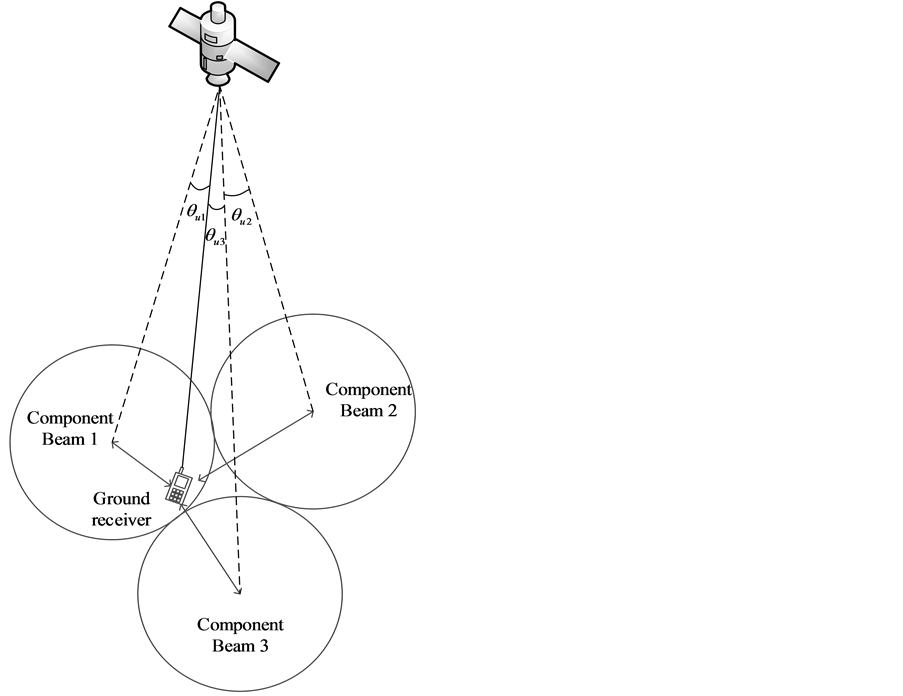
As is shown in Figure 1, the distance of ground receiver to center of component beam is different, which makes the signal strength varies.
Figure 2 shows the space relationship among satellite, user u and component beam center n. h is the height of satellite orbit. R is radius of the earth.
According to Figure 2, suppose that 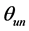 is the angle of ground receiver u to satellite and component beam center n to satellite,
is the angle of ground receiver u to satellite and component beam center n to satellite,  can be given by
can be given by
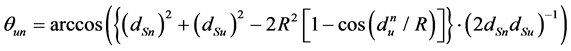 (1)
(1)
where dSn and dSu are the distance between satellite and component beam center n and user u respectively. 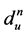 is the distance between sub-satellite point and user u.
is the distance between sub-satellite point and user u.
Figure 1. Component beam schematic diagram.
Suppose that  is the normalized far-field radiation pattern of component beam, the adoption of different radiation pattern results different antenna gain, when the direction angle is the same.
is the normalized far-field radiation pattern of component beam, the adoption of different radiation pattern results different antenna gain, when the direction angle is the same. 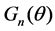 represents the antenna gain of the nth component beam. The
represents the antenna gain of the nth component beam. The  can be written as
can be written as
 (2)
(2)
where  can be calculated by (1), Gmax,n is the maximum gain of the nth component beam.
can be calculated by (1), Gmax,n is the maximum gain of the nth component beam.
2.2. Mobile Satellite Channel Model
In satellite communication, a signal is fading during propagation. Those fading may cause by environment and various attenuation facts, for instance cloud attenuation, rain attenuation and ionospheric scintillation. Taking into account this paper research mainly discusses spatial correlation, since attenuation facts like cloud attenuation and ionospheric scintillation are stay the same for a long time, we focus on the influence of ground environment near receiver, namely the multipath which arise from scattering, reflection, refraction or diffraction of the radiated energy off scatterers that lie in the environment.
For satellite communication, typically the height of the ground receiver is lower than nearby scatterers. The received signals in the both horizontal and
Figure 2. Three-dimension component beam model.
vertical plane are distributed. While establishing the channel model, we need to consider the height of scatterers, so the traditional two-dimensional geometric channel model no longer applies. Assuming that scatterers are distributed in a right cylinder which has ground receiver as it bottom center, a three-dimension geometry channel model is shown in Figure 3. A large picture of ground receiver in the model is shown in Figure 4.
For a downlink of satellite communication system, we assume that p and q are the number of satellite antennas, l and m are the number of ground antennas,
 . Nr and Nr are the maximum number of transmitting antenna and receiving antenna. The received signal is given by
. Nr and Nr are the maximum number of transmitting antenna and receiving antenna. The received signal is given by
 (3)
(3)
where, H(t) is channel impulse response, n(t) is noise.  represents convolution.
represents convolution.
The received signal includes direct-path and multipath component in satellite communication system. So the channel impulse response is given by
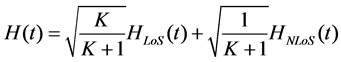 (4)
(4)
where HloS(t) is impulse response of direct-path, HNLoS(t) is impulse response of multipath. HloS(t) and HNLoS(t) are both NT × NR matrix. K is Rician Index, which describes ratio of direct-path power and multipath power (unit is dB). The value of K depends on angel of elevation from ground receiver to satellite, carrier frequency and environment around receiver. In this paper, since the interval between ground antennas is much small than shadow fading in different states, we
Figure 3. 3-Dimension geometry channel model.
Figure 4. Large picture of ground receiver.
can approximate that received signal shallow fading of two antennas are the same.
In the model shown in Figure 3 and Figure 4, Rm and Rl are the mth and the lth antenna in ground receiver respectively, Tp and Tq are the pth antenna and the qth antenna in satellite respectively. x − y plane is parallel to horizontal surface, and is perpendicular to OOR. OR is the midpoint of two antennas Rm and Rl ground projection line. OS is the point of intersection of x axis and y axis and also the midpoint of x − y plane projection line of two antennas Tp and Tq. OT is the center of transmitting antenna array. HS,max is the maximum height of scatterers distribution. RS,max is the maximum range of scatterer distribution (the maximum radius). 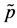
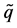
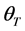
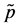
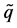

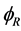
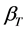
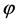
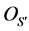
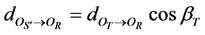
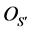

According to the model, the impulse responses of sub channel from Tp to Rl can be written as
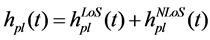
Since the large number of hypothetical scatterers in the model, let Sn be the nth scatterer. Let RS,max and HS,max represent the radius and height of cylinder in the model, namely, the maximum distance and height of scatterers distribution. RS(n) is the distance between OR and Sn projection in x-y plane,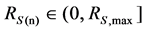

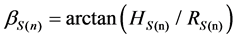
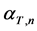
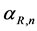
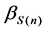
In multi-beam channels of mobile satellite system, the impulse responses of sub channel from Tp to Rl can be written in terms of (5). Considering the influence from component beam on to received signal, the direct-path component of the channel response can be written as
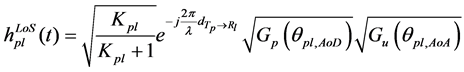
And multipath component of the channel response can be written as
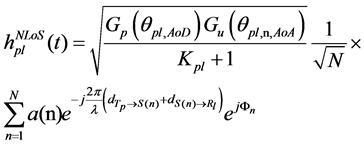
For the large number of scatterers, according to Central Limit Theorem, 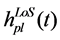
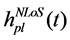
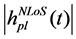
In (6), 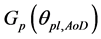
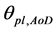
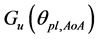
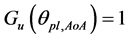
In (7), 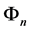
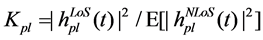
3. Multi-Beam Spatial Correlation Characteristics
3.1. Definition of Spatial Correlation
In the early stage of channel research, multi-antenna technology will get a huge channel capacity upgrade in the independent and identically distributed (iid) Rayleigh channel [5] [6], under the assumption that the interval between the antennas is large enough and the angle of arrival (AOA) angular spread is sufficiently large. However, in an actual mobile communication system, the angular spread of the received signal AOA is not large enough under the affection of the interval among antennas and scatterers distribution around. It results that the fading of received signal among different antennas and the signal received among the same antenna from different transmitting antenna are not statistically independent. So the correlation exists. This correlation is called by spatial correlation, its definition is written as
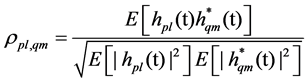
where p and q are two transmitting antennas. l and m are two receiving antennas. hpl(t) represents channel response of antenna p to l. In the same way, hqm(t) represents channel response of antenna q to m. E[•] is expectation. ρpl,qm is correlation coefficient between received signal of antenna l and m.
3.2. Analysis of Multi-Beam Spatial Correlation
Since 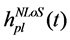


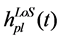
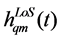
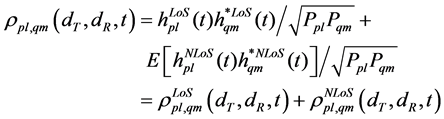
According to the model shown in Figure 3. The spatial correlation coefficient of direct-path component is
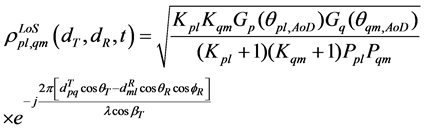
where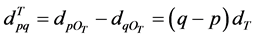

Also, the spatial correlation coefficient of multipath component is
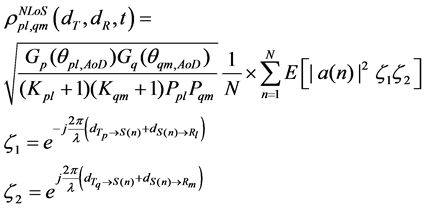
Since the large number of scatterers around ground receiver antennas (a larger number N), RS, HS and αR can replace the discrete variables RS(n), HS(n) and αR,n as an approximation. (11) can change into integral form
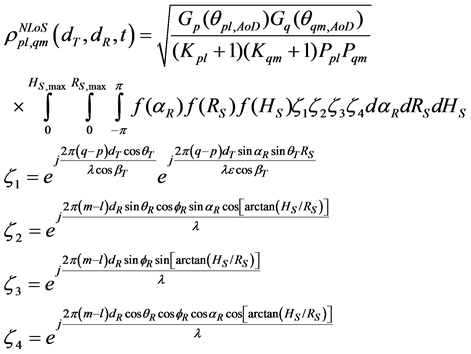
RS, which is the distance of scatterer and ground receiver, can be described by hyperbolic distribution [4]. The height of scatterer HS, which PDF depends on environment around receiver, is normally described by normal distribution [7], Lon-normal distribution [8] etc. The normal distribution is used for modeling in this paper. In ground wireless communication system, the arrival angle of multipath signal is described by evenly distribution [9] or Laplace distribution. But in mobile satellite communication system, Laplace distribution is more suitable under testing in urban area [10], which is affected by the number and the distribution of scatterers around ground receiver.
When the arrival angle of received signal in x-y plane αR is Laplace distribution, the spatial correlation coefficient of multipath component in the received signal is shown as
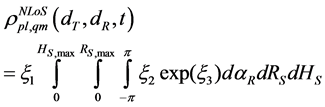
where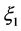
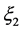
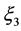
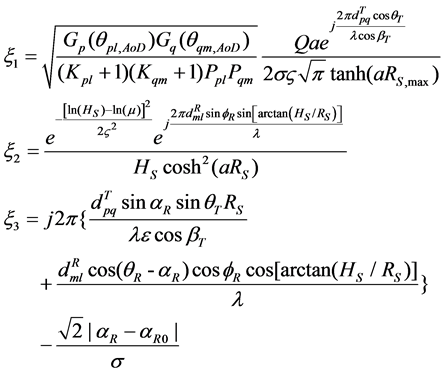
4. Numeric Results and Analysis
In this part, the channel spatial correlation coefficient of the signal received by ground antennas is obtained by numeric calculation in multi-beam satellite communication system, which adopt parabolic reflector antenna. All the parameters of simulation are given in Table 1, if not specified otherwise.
The calculation is on the assumption of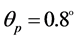
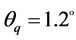
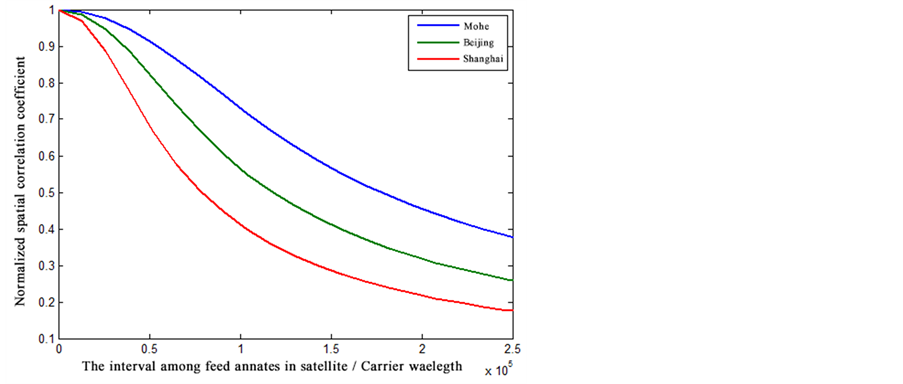
Figure 5 shows that in term of nT = 2, nR = 1, the relationship between ground spatial correlation coefficient among three Chinese cities, namely Mohe, Beijing and Shanghai, and the interval of satellite antennas.
As shown in Figure 5, with the increase of the antenna interval, spatial correlation coefficient among satellite channel showed a decreasing trend, and the higher the latitude, the slower decline.
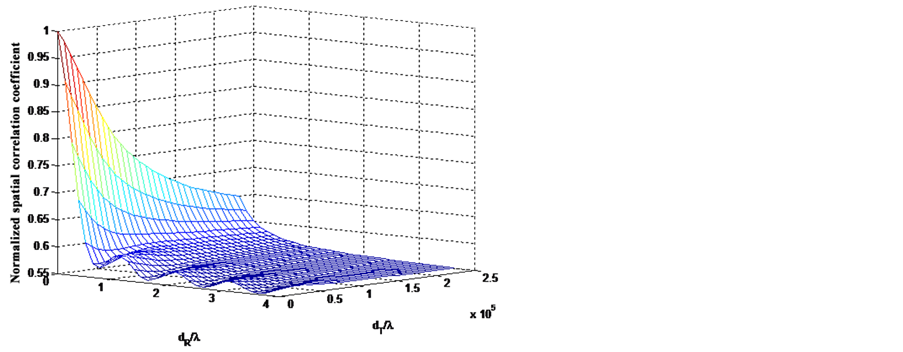
Take Beijing as example, let K = 4 dB, Figure 6 shows the relationship among the interval of satellite antennas, ground antennas, and the spatial correlation
Figure 5. Relationship between the component beam correlation coefficient and the interval of satellite antennas.
Figure 6. Relationship among the interval of antennas and spatial correlation coefficient.
Table 1. Simulation parameter.
coefficient. With the interval increasing, spatial correlation coefficient showed a decreasing trend, but when the interval is small, the spatial correlation coefficient is still large.
5. Summary/Conclusion
In this paper, considering that the radio transmission feature and the antenna array feature the affection influence the spatial correlation coefficient, we create a 3-demension channel model. According to the model, we derive the spatial correlation coefficient among component beam which received by ground receiver with numeric calculation and analysis. The result shows that spatial correlation coefficient is still large even if the interval of antennas is small. Therefore, the spatial correlation coefficient cannot be ignored in satellite channel research.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (No.61371073).
Cite this paper
Su, Z.M., Fei, X., Cheng, Y.X. and Wu J.J. (2017) Spatial Correlation Characteristics Analysis of Multi-Beam Channels of Mobile Satellite System. Int. J. Communications, Network and System Sciences, 10, 127-137. https://doi.org/10.4236/ijcns.2017.105B012
References
- 1. G.Grillo, Shiu, D.S., Foschini, G.J., Gans, M.J. and Kahn, J.M. (2000) Fading Correlation and Its Effect on the Capacity of Mul-tielement Antenna Systems. IEEE Transactions on Communications, 48, 502-513. https://doi.org/10.1109/26.837052
- 2. Abdi, A. and Kaveh, M. (2002) A Space-Time Correlation Model for Multielement Antenna Systems in Mobile Fading Channels. IEEE Journal on Selected Areas in Communications, 20, 550-560. https://doi.org/10.1109/49.995514
- 3. Seedahmed, S.S., Mahmoud, S., Zahir, Z.M., Hussain, M. and O’Shea, P.P. (2002) Geometrical Model for Mobile Radio Channel with Hyperbolically Distributed Scatterers. Proc. 8th IEEE Int. Conf. Communications Systems, Singapore, November 2002.
- 4. Mahmoud, S.S., Hussain, Z.M. and O’shea, P. (2002) A Space-Time Model for Mobile Radio Channel with Hyperbolically Distributed Scatterers. Antennas and Wireless Propagation Letters, 1, 211-214. https://doi.org/10.1109/LAWP.2002.807961
- 5. Foschini, G.J. and Gans, M.J. (1998) On Limits of Wireless Communications in a Fading Environment When Using Multiple Antennas. Wireless Personal Communications, 6, 311-335. https://doi.org/10.1023/A:1008889222784
- 6. Telatar, E. (1999) Capacity of Multi-Antenna Gaussian Channels. European Trans-actions on Telecommunications, 10, 585-595. https://doi.org/10.1002/ett.4460100604
- 7. Saunders, S. and Evans, B. (1996) Physical Model of Shadowing Probability for Land Mobile Satellite Propagation. Electronics Letters, 32, 1548-1549. https://doi.org/10.1049/el:19961058
- 8. Tzaras, C., Evans, B. and Saunders, S. (1998) Physical-Statistical Analysis of Land Mo-bile-Satellite Channel. Electronics Letters, 34, 1355-1357. https:/.doi.org/10.1049/el:19980937
- 9. Salz, J. and Winters, J.H. (1994) Effect of Fading Correlation on Adaptive Arrays in Digital Mobile Radio. IEEE Transactions on Vehicular Technology, 43, 1049-1057. https://doi.org/10.1109/25.330168
- 10. Abdi, A., Barger, J.A. and Kaveh, M. (2002) A Parametric Model for the Distribution of the Angle of Arrival and the Associated Correlation Function and Power Spectrum at the Mobile Station. IEEE Transactions on Vehicular Technology, 51, 425-434. https://doi.org/10.1109/TVT.2002.1002493