International Journal of Communications, Network and System Sciences
Vol.10 No.05(2017), Article ID:76553,11 pages
10.4236/ijcns.2017.105B011
Capacity Analysis and Optimization of Satellite MIMO System
Haijin Li, Jianbo Li, Yuxin Cheng, Jianjun Wu*
Institute of Advanced Communications, EECS, Peking University, Beijing, China




Received: March 15, 2017; Accepted: May 23, 2017; Published: May 26, 2017
ABSTRACT
Multiple-Input Multiple-Output (MIMO) technology is widely applied in terrestrial wireless communication system, which greatly increases the system capacity. Satellite communication system has many advantages such as wide coverage and strong flexibility. Therefore, how to make a better use of MIMO technology in satellite communication system has become a research hotspot in recent years. The purpose of this paper is to analysis the relationship between satellite MIMO system capacity and parameters of terrestrial antenna such as angle and distance. The parameters of terrestrial antenna were derived and calculated to keep a higher capacity for satellite MIMO system. Numerical analysis of system capacity performance before and after optimization was obtained, which proved the correctness of the theory proposed in this paper.
Keywords:
MIMO, Satellite Communication, System Capacity, Capacity Analysis, Capacity Optimization

1. Introduction
Multiple-Input Multiple-Output (MIMO) technology is widely applied in modern communication system. It provides users with a higher data rate, better service quality and greater network capacity [1]. Compared to terrestrial communication system, satellite communication system has many advantages such as wide coverage, flexible connection, and little influence by topography, etc. It is widely used in the fields of transoceanic television broadcasting and telephone, communication in remote areas, maritime and aeronautical communication, navigation positioning and military communication. Because of the huge potential of MIMO technology to increase the system capacity, the application of MIMO technology in satellite communication system becomes a hot topic. In recent years, scholars have carried on a large amount of researches about satellite MIMO communication.
In 2005, P. R. King provided a model of distributed satellite MIMO channel [2], and then in second year, he completed a similar analysis and research on the polarized satellite MIMO channel, which shows the benefits of using MIMO in satellite communication [3]. Sellathurai also proposed a simplified statistical model of polarized satellite MIMO channel [4]. Benjamin Ros proposed a system scheme for interactive satellite MIMO communication using the OFDM system. He compared the performance of satellite MIMO system with multi-antenna SISO system under DVB-SH standard, and the results indicate that MIMO technology is necessary for satellite communication [5].
Compared with the abundant research results of satellite MIMO, the investigations about optimization of satellite MIMO system capacity are limited. How to improve the system capacity of satellite MIMO system is worthy of research and analysis. In this paper, we provide theoretical calculation of the system capacity of GEO and LEO satellite MIMO system, and then complete the optimization of system capacity. Especially for LEO satellites, we carry out the numerical analysis, which proves the correctness of the theory proposed in this paper.
2. System Model
Satellite system can be divided into GEO system and non-GEO system. Because the GEO system is relatively geostationary, MIMO system using GEO is more stable. The existing GEO systems are Inmarsat system and Thuraya system, but they both only have three satellites. The beam overlap area is not large enough since the number of satellites is too small. Thus, it is impossible to achieve MIMO system using multiple GEO satellites in most areas on the ground.
The orbit altitude of LEO satellite system is 700 to 1500 km, moving at a high speed relatively to the earth. Globalstar system and Iridium system are major existing LEO satellite communication systems until now, which respectively have 48 and 66 LEO satellites completing global coverage. The existing LEO satellites are abundant resources, and users can simultaneously connect multiple satellites in most areas of the Earth. Thus, there are enough LEO satellites to build MIMO system.
As shown in Figure 1, we consider a complete closed-loop scenario. The whole satellite MIMO system contains three components as follows.
Terrestrial transmitting terminal: The transmitter is generally a terrestrial station. It is mainly responsible for controlling, scheduling, and connecting the ground network and the user terminal in the entire communication process.
Communication satellite: Generally, there are two or more satellites, playing a role as relaying and forwarding in the whole communication system. The signal transmitted by the ground station is delivered to the user terminal through transparent forwarding or decode-and-forwarding.
User terminal: It could be hand-held mobile terminals, or terminals on-board, ship-borne and air-borne moving at a high speed, or even another fixed ground station.
Figure 1. Satellite MIMO system model.
General system includes two links: The uplink is from ground station to the satellite system and downlink is from satellite system to the user terminal. Maybe there also exist inter-satellite links among the satellites to assist communication.
In Figure 1, 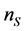 is the number of antenna of the ground transmitter,
is the number of antenna of the ground transmitter, 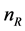 is the number of antennas of the relay satellite and
is the number of antennas of the relay satellite and 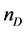 is the number of antenna of the receiver on the ground. In general,
is the number of antenna of the receiver on the ground. In general,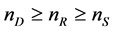 .
.
3. Capacity Analysis and Optimization
3.1. Capacity Analysis
In satellite communication systems, the satellite channel is significantly different from the terrestrial channel, because the power of its direct path is much greater than that of the multipath. For example, according to the data from ITU-R M.1225 [6], the power of direct path is about 20 dB greater than the maximum multipath. In fact, because the signal energy in NLOS channel signal is too small, the multipath signal has little effect on the capacity of the system compared with the existence of direct path [7]. Therefore, in this paper we only consider the influence of direct path.
In consideration of the free space propagation of the direct path through satellite-ground channel, the channel function can be expressed as [8]
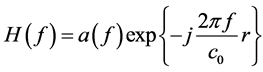 (1)
(1)
where r denotes the distance between the transmitter and the receiver, 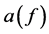 denotes the signal amplitude attenuation when passing through the channel. Thus for 2*2 MIMO the capacity can be represented as
denotes the signal amplitude attenuation when passing through the channel. Thus for 2*2 MIMO the capacity can be represented as
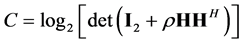 (2)
(2)
where  denotes the system SNR removing the channel fading part. The channel matrix H is expressed as
denotes the system SNR removing the channel fading part. The channel matrix H is expressed as
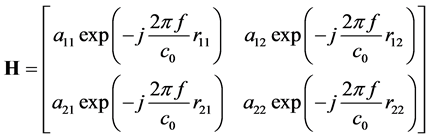 (3)
(3)
We establish an unified coordinate system to analyse and calculate the difference between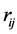 . It is shown in Figure 2 and Figure 3.
. It is shown in Figure 2 and Figure 3.
As shown in Figure 2, we define the equatorial plane as XOY plane, the polar direction as Z-axis. Besides, OX axis intersects 0 degrees’ east longitude and OY axis intersects 90 degrees’ east longitude. The two red circles in Figure 2 represent the location of ground terminal antennas. 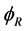 represents the latitude of ground terminals and
represents the latitude of ground terminals and 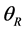 represents the longitude of ground terminals (East longitude is positive and West longitude is negative).
represents the longitude of ground terminals (East longitude is positive and West longitude is negative). 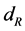 denotes the distance between two antennas on the ground, and
denotes the distance between two antennas on the ground, and 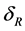 denotes the angle between two antennas and east direction. Then the coordinates of the two antennas on the ground are respectively expressed as
denotes the angle between two antennas and east direction. Then the coordinates of the two antennas on the ground are respectively expressed as
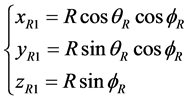 (4)
(4)
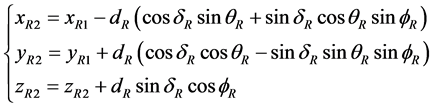 (5)
(5)
Because the coordinates of two satellites are not necessarily related, we analyze a single satellite coordinates respectively. Satellite coordinate is shown in Figure 3.
The dotted line circle in Figure 3 is the orbit of satellite. A point is the ascending node (the intersection point of satellite orbit and the equatorial plane) of this orbit,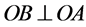 . S is the satellite position.
. S is the satellite position. 










Figure 2. Terrestrial terminal coordinate.
Figure 3. Satellite coordinate.
where

H is the orbit altitude of the satellite. Two satellites have different





3.2. Parameter Optimization of GEO System
Figure 4 is a schematic diagram of the GEO satellite MIMO coordinate. It is necessary to discuss the optimization of distance and angle between antennas, so that we can always keep the system capacity in the optimal value.
First, put Formula (3) into Formula (2). Capacity can be expressed as

Figure 4. GEO satellite MIMO coordinate.
where 


In order to maximize C, the following expression should be guaranteed

In the GEO system, the satellite is fixed relatively to earth, and the rotation of the earth 



Put Formula (12) into Formula (4), we obtain

Put Formula (12) into Formula (5), we obtain

Let




Then by exploiting the small aqueous formula

Put Formulas (14) and (18) into (11), it can be obtained that when place angle 


It can be seen that the optimal value of the terrestrial antenna is periodic variation. In the same way, let


Put Formula (20) and (21) into (19), It can be obtained that when 


3.3. Parameter Optimization of LEO System
In the LEO satellite system, there exists an angle between the satellite orbit plane and the equatorial plane, in addition, the angular velocity of satellites and the earth is different, so 


First, we calculate the distance 

Let


Make use of Formulas (4) and (7). After simplification, we obtain

Set the variable


where

Then by exploiting the small aqueous formula

When place angle 


In this formula, it is obvious that the optimum value of ground antennas changes periodically. Similarly, let


When 


4. Numerical Analysis Results
Through the analysis above, it can be seen that optimum channel capacity of GEO and LEO satellite MIMO system is related to 

In order to calculate LEO satellite MIMO system through numerical analysis, orbit parameters of Globalstar system and Iridium system are needed. We also need to determine the system SNR 




System capacity of satellite MIMO system is closely related to the arrangement of ground antennas. The system capacity can be maintained at a optimal value by using tracking antenna chrtrolling 

Table 1. Main parameters in numerical analysis.
Figure 5. Tracking antenna performance (d = 0.2 m).
Figure 6. Tracking antenna performance (d = 2 m).
the system capacity of tracking antennas is significantly improved compared with the fixed antennas in both systems. The tracking antenna makes the system maintain a high and relatively fixed system capacity.
From Figure 5 and Figure 6, we can see the different capacity performance when the antenna spacing 
5. Conclusion
In this paper, we have analyzed the relationship between the capacity performance of satellite MIMO system and placement parameters of terrestrial antennas such the angle and distance. The numerical calculation verifies the possibility to optimize the parameters. Later, through formula derivation we obtain the time variation function of the optimal placement angle and distance of the ground antenna. Finally, numerical analysis is carried out according to the initial position of satellite in the practical system. The results demonstrate that the system capacity can be significantly improved when the antenna is traced using the theoretical analysis results.
Acknowledgements
This paper is supported by the National Natural Science Foundation of China # 61371073.
Cite this paper
Li, H.J., Li, J.B., Cheng, Y.X. and Wu, J.J. (2017) Capacity Analysis and Optimization of Satellite MIMO System. Int. J. Communications, Network and System Sciences, 10, 116-126. https://doi.org/10.4236/ijcns.2017.105B011
References
- 1. G.Grillo, Gesbert, D., Shafi, M., Shiu, D.-S., et al. (2003) From Theory to Practice: An Overview of MIMO Space-Time Coded Wireless Systems. IEEE Journal on Selected Areas in Communications, 21, 281-302. https://doi.org/10.1109/JSAC.2003.809458
- 2. King, P.R., Evans, B.G. and Stavrou, S. (2005) Physical-Statistical Model for the Land Mobile-Satellite Channel Applied to Satellite/HAP-MIMO. 11th European Proceedings of the Wireless Conference 2005-Next Generation Wireless and Mobile Communications and Services (European Wireless).
- 3. King, P.R. and Stavrou, S. (2006) Capacity Improvement for a Land Mobile Single Satellite MIMO System. IEEE Antennas and Wireless Propagation Letters, 5. https://doi.org/10.1109/lawp.2006.872439
- 4. Sellathurai, M., Guinand, P. and Lodge, J. (2006) Space-Time Coding in Mobile Satellite Communications Using Dual-Polarized Channels. IEEE Transactions on Vehicular Technology, 55, 188-99. https://doi.org/10.1109/TVT.2005.861195
- 5. Ros, B., Lacoste, F., Scot, G., et al. (2009) Increasing Reliability of an Interactive Mobile Satellite Telecommunication System Using Diversity and MIMO Schemes. 2009 International Conference on Proceedings of the Wireless Communications & Signal Processing. https://doi.org/10.1109/WCSP.2009.5371395
- 6. Recommendation, I. (1997) Guidelines for Evaluation of Radio Transmission Technologies for IMT-2000. International Telecommunication Union.
- 7. Knopp, A., Schwarz, R.T., Hofmann, C.A., et al. (2007) Measurements on the Impact of Sparse Multipath Components on the LOS MIMO Channel Capacity. 4th International Symposium on Proceedings of the Wireless Communication Systems https://doi.org/10.1109/iswcs.2007.4392301
- 8. Oh, C.-I., Choi, S.-H., Chang, D.-I., et al. (2006) Analysis of the Rain Fading Channel and the System Applying MIMO. International Symposium on Proceedings of the Communications and Information Tech-nologies. https://doi.org/10.1109/iscit.2006.340001








