International Journal of Communications, Network and System Sciences
Vol.10 No.05(2017), Article ID:76531,8 pages
10.4236/ijcns.2017.105B004
Achieving 100% Throughput for Integrated Uni- and Multicast Traffic without Speedup
Fulong Yan, Qingxu Xiong, Han Xiao, Jiacheng Liang
Electrical Engineering School, Beihang University, Beijing, China




Received: March 5, 2017; Accepted: May 23, 2017; Published: May 26, 2017
ABSTRACT
Along with the unbounded speedup and exponential growth of virtual queues requirement aiming for 100% throughput of multicast scheduling as the size of the high-speed switches scale, the issues of low throughput of multicast under non-speedup or fixed crosspoint buffer size is addressed. Inspired by the load balance two-stage Birkhoff-von Neumann architecture that can provide 100% throughput for all kinds of unicast traffic, a novel 3-stage architecture, consisting of the first stage for multicast fan-out splitting, the second stage for load balancing, and the last stage for switching (FSLBS) is proposed. And the dedicated multicast fan-out splitting to unicast (M2U) scheduling algorithm is developed for the first stage, while the scheduling algorithms in the last two stages adopt the periodic permutation matrix. FSLBS can achieve 100% throughput for integrated uni- and multicast traffic without speedup employing the dedicated M2U and periodic permutation matrix scheduling algorithm. The operation is theoretically validated adopting the fluid model.
Keywords:
Speedup, Multicast, Switch Architecture, 100% Throughput

1. Introduction
With the rapid development of the emerging media communication, including network television, video conference, and teleconference, the amount of multicast traffic is increasing enormously. Compared with unicast traffic using N virtual output queuings (VOQs) to avoid the head-of-line (HoL) blocking, the VOQs needed for avoiding multicast traffic HoL is 2N−1, which is known as multicast virtual output queuing (MC-VOQ) [1] and is not practical in even medium-size switches due to the poor scalability. Therefore, a feasible solution is to allocate k (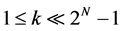 ) FIFO queues at each input for all multicast traffic. However, the HoL can only be relieved but not eliminated completely in this k-MC-VOQ architecture [2] [3] [4].
) FIFO queues at each input for all multicast traffic. However, the HoL can only be relieved but not eliminated completely in this k-MC-VOQ architecture [2] [3] [4].
When the maximum weight matching (MWM) algorithm is employed in the unbuffered crossbar switch with N ports, at least a speedup of 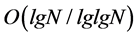 is necessary for admissible multicast traffic to achieve 100% throughput [5]. As for the multicast scheduling in combined input and crosspoint queued (CICQ), to achieve 100% throughput, a speedup of
is necessary for admissible multicast traffic to achieve 100% throughput [5]. As for the multicast scheduling in combined input and crosspoint queued (CICQ), to achieve 100% throughput, a speedup of 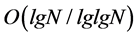 is necessary when the crosspoint buffer (XB) size is fixed [6]; to the contrary, while the speedup keeps constant, the XB size will be scaled in the order of
is necessary when the crosspoint buffer (XB) size is fixed [6]; to the contrary, while the speedup keeps constant, the XB size will be scaled in the order of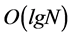 . The performance of multicast scheduling in k-MC-VOQ architecture is studied through simulations by Gupta and Aziz [2], and theoretically analyzed by S.Min [7] and W. Zhu [8]. Both the simulations and theoretical results have shown that 100% throughput cannot be achieved in single-stage switching architecture without speedup. In [9], 100% throughput is achieved in a two-stage architecture with 2× speedup. The speedup needed put forward stringent switching time requirement in the operation of switching matrix as the link rate increase beyond 10 Gbit/s. Therefore, we are motivated to find the novel switch architecture and scheduling algorithm for efficiently switch-processing the multicast traffic without speedup.
. The performance of multicast scheduling in k-MC-VOQ architecture is studied through simulations by Gupta and Aziz [2], and theoretically analyzed by S.Min [7] and W. Zhu [8]. Both the simulations and theoretical results have shown that 100% throughput cannot be achieved in single-stage switching architecture without speedup. In [9], 100% throughput is achieved in a two-stage architecture with 2× speedup. The speedup needed put forward stringent switching time requirement in the operation of switching matrix as the link rate increase beyond 10 Gbit/s. Therefore, we are motivated to find the novel switch architecture and scheduling algorithm for efficiently switch-processing the multicast traffic without speedup.
Different from the existing single-stage and multi-stage architectures, we proposed a novel three-stage architecture that can achieve 100% throughput without speedup. The first stage performs the multicast fan-out splitting (FS), which is a multicast transformed to unicast switch fabric. We also develop the dedicated novel scheduling algorithm for the first stage. The second stage is an unbuffered crossbar and executes the load balance (LB), while the last stage VOQ carries out the switching function (S). The proposed FSLBS architecture inherits the advantage of low implementation complexity of the load balancing two-stage architecture, and the theoretical investigation with fluid model confirms that FSLBS can achieve 100% throughput without speedup.
2. System Architecture and the Algorithm
2.1. Three-Stage Switch Architecture
As shown in Figure 1, the proposed 3-stage switch architecture is composed of the first multicast fan-out splitting CICQ stage, the second load balance crossbar stage and the third switching VOQ stage. In Figure 1, N FIFO queues with infinite buffer size are maintained at each input port of the first CICQ stage. The fixed-size packet transmitted by the switch fabric is called a cell. We consider only the fan-out splitting discipline that multicast cells may be delivered to outputs over several slots. Any multicast cell is characterized by its fan-out set, i.e., by the set of outputs to which the cell is directed. We define the fan-out size f as the number of destinations of a multicast cell. Arriving multicast and unicast cells are partitioned into the N queues according to the value of f. In this work, a novel cell assignment algorithm assigning the queue for cells based on f is proposed, and we concentrate on the issue related to the traffic scheduling. It can be clearly seen from Figure 1 that the second stage switch fabric is just an ordinary
Figure 1. The 3-stage architecture composed of CICQ, Crossbar and VOQ.
unbuffered crossbar switch performing load balance operation with permutation matrices, the details of the operation for load balancing are shown in II.C [10]. The third stage is a VOQ switch architecture, and N VOQs are maintained at each input port. VOQi,j is the virtual output queue for cells from input i to output j at the third stage, also it is the j-th queue at the input i in Figure 1.
2.2. The Scheduling Algorithm of the First Stage
The key point of the scheduling algorithm is that multicast cell is fan-out split to unicast cell. There are N FIFO queues in the input side of the first stage. At each input i, based on the fan-out size f of the coming uni- and multicast traffic (the f of unicast equals 1), the cell with fan-out equals k are allocated in the k-th queue. For instance, the unicast cell are assigned to the first queue, while the broadcast cell (f = N) accesses the N-th queue.
Let XBi,j (buffer size equals 1) be the crosspoint buffer connects input i and output j, and define EIQ(i) to be the XB set that belongs to input port i, namely EIQ(i) = {XBi,j |j = 1, …, N}, and EOQ(j) is the XB set that corresponds to output port j, EOQ(j) = {XBi,j|i = 1, …, N}. The priority of the inputs with non-empty queues is sorted based on their input port number k. Each input port i preserves a weight point WP(i) for the scheduling priority of the N queues, and WP(i) points to the non-empty queue that contains cells with the largest f, namely,
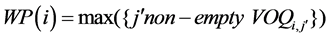 (1)
(1)
There is also a XB initial address pointer XP(i) for input port i, and at the beginning of the scheduling, XP(i) is initialized to 1. Denote 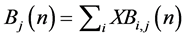 as the number of cells queued at all XBs destined to output j at the beginning of slot n. In each slot n, the output port j with
as the number of cells queued at all XBs destined to output j at the beginning of slot n. In each slot n, the output port j with 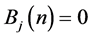 has the higher priority and will be matched prior to other output ports, and ties are broken by the least output number.
has the higher priority and will be matched prior to other output ports, and ties are broken by the least output number.
The length of EIQ(i) is denoted by Li. After each scheduling slot, XP(i) is renewed to the address of non-empty XBi,j' with the least j':
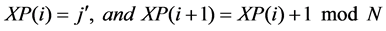 (2)
(2)
Since one-to-one matching is not required, the scheduling is much simpler than MWM algorithm. And the output scheduling adopts simple Round Robin (RR) algorithm. The pseudo-code of the M2U algorithm is presented below.
Initialization: 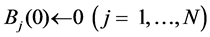
M2U works as follows:
1) Find out input ports with non-empty queues, and sort them in the increasing order of port number.
2) Sort outputs in the increasing order of Bj(n).
3) For each sorted input i do
4) Schedule the queue (cell with fan-out size f) that WP (i) points.
5) Sort the empty XBi,j in the EIQ(i) in the order of the sorted output list.
6) if f ≤ N − Li
7) the cell is split to the fXBi,j, and for the corresponding output j, Bj(n) = Bj(n) + 1.
8) Else
9) The cell is split into N − Li + 1 portions, N − Li portions are buffered in the empty XBi,j.
10) The fan-out splitting residual with fan-out size f1 = f − (N − Li) are re-buffered in queue f1, and for the corresponding output j, Bj(n) = Bj(n) + 1. go to 2).
For output scheduling works with RR. Bj(n) = Bj(n) − 1.
Figure 2 shows an example of the M2U algorithm for a 4 × 4 switch. At slot n, the input 1 has a multicast cell with fan-out set {2, 3} and a broadcast cell, input 2 only has a unicast cell destines to output 4. Queues of input 3 are empty while the input 4 has a multicast cell with fan-out set {1, 3, 4}. There are 5 XBs, namely, XB1,4, XB3,1, XB3,4, XB4,1, XB4,4 are occupied, while the rest XBs are empty and ready for buffering cells. Based on the principle of M2U algorithm, the broadcast cell in queue 4 at input 1 has priority, while the output 2 and 3 with Bj(n) = 0 has priority. Therefore, the broadcast cell is split into 4 unicast cells and cell with destination 1, 2, 3 are buffered in XB1,2, XB1,3, XB1,1, respectively, and the residual with destination 4 will be re-buffer in queue 1. For the input 2, there is only a unicast cell, and the output 2 and 3 with EOQ length of 1 after output port re-sorting has the priority, so the cell are buffered in XB2,2. Similar to the input 1, the multicast cell at input 4 is split into 3 unicast cells and cell with
Figure 2. An example of the M2U for the first stage CICQ.
destination 1, 3 are buffered in XB4,3, XB4,2, respectively.
2.3. The Scheduling Algorithm of the Last Two Stages
The second stage is a crossbar switch without any buffer. Cells arriving at inputs of the second stage at time t are switched instantly to the third stage. Suppose that P is any one-cycle permutation matrix with N rows and columns. And circular-shift matrix with Pi,j = 1 only when j = i + 1 mod N is such a needed matrix. Given Pk = Pk, PN will be an identity matrix. Assuming A(t) is the traffic matrix entering the second stage, while B(t) is the traffic matrix exiting the second stage, and let P(t) be the N × N permutation matrix allocated at time t at the second stage. Then we get
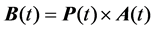 (3)
(3)
when we set up the permutation matrices P(t) periodically using Pk(k = 1, …, N), then load balancing is performed at the second stage. For the third stage, the buffer size of the VOQs is assumed infinite, and the same periodic permutation matrix Pk (k = 1, …, N) are allocated, which means that each input and output pair is assigned a time slot during every N time slots. More precisely, the allocated rate for each input and output pair is 1/N. Therefore, 100% throughput can be achieved in the third stage for all the admissible traffic feed in the system under full load since the traffic is uniform at the third stage, which is just what we already get from the second stage. For the parameter of latency, the third stage contribute the majority for the three contentions existed in the VOQ architecture while the second stage only introduce 1 slot. The total latency of the proposed architecture should be less than other architectures in principle under full load because it’s stable.
3. Performance Analysis
The stability of system means the 100% throughput can be achieved in the switch architecture. In brief, if the queue length of every port is bounded when the load of the system is affordable, then the schedule is stable.
Definition 1 (Stability) In a N × N (N > 1) switch architecture, if all the queued cells can be scheduled in a finite time, the switch architecture is stable.
The stability of the first stage CICQ is analyzed using the fluid model technique [10]. Let Ai,j,F(n) be the number of cells destining output j at the input i in the period of slot 0 to slot n with Ai,j,F(0) = 0. F denotes the fan-out set of the multicast cell. When it is a unicast, fan-out size f = 1 and fan-out set F only has an element j. If the arrival rate of cells with a specific fan-out F is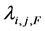 , then we have
, then we have
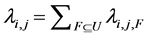 (4)
(4)
The arrival process {Ai,j,F(・), i, j = 1, …, N } comply with a strong law of large numbers if equation (5) holds:
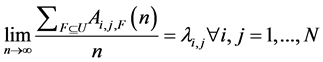 (5)
(5)
where 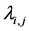 is the arrival rate of cells that output j belongs to fanout F with regard to input i. For any arrival process that Equation (5) holds, The traffic is regarded as admissible when Equation (6) meets, that is to say, all inputs and outputs are non-oversubscribed:
is the arrival rate of cells that output j belongs to fanout F with regard to input i. For any arrival process that Equation (5) holds, The traffic is regarded as admissible when Equation (6) meets, that is to say, all inputs and outputs are non-oversubscribed:
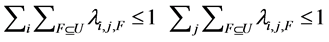 (6)
(6)
Take Di,j(n) as the number of departures from XBi,j during time slot [0, n] (Di,j(0) = 0). 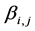 is denoted as the arrival rate of cells allocated to the XBi,j, if Equation (7) holds:
is denoted as the arrival rate of cells allocated to the XBi,j, if Equation (7) holds:

The switch architecture running on such a matching algorithm is regarded to be rate stable, which is the same meaning as achieving 100% throughput.
Theorem 1: The first stage switch architecture is rate stable under any admissible integrated uni- and multicast traffic that satisfies strong law of large numbers when it operates under the M2U algorithm combined with work-conserving output RR arbiters.
Proof: If the corresponding fluid model of the switch is weakly stable, a switch will be rate stable, i.e., for every fluid model solution (D, T, Z) with Z(0) = 0, Z(t) = 0 (t ≥ 0). Consider the fluid model of a CICQ switch operating under the M2U algorithm. Let (D, T, Z) be a fluid model solution with Z(0) = 0, and Z(t) be the total amount of fluid queued at all the N2 input FIFO queues and N2 XBs at time t. From Lemma 1 in [10], if 


1)
2)
In both cases, 


Applying the fluid limit procedure and (6), we have:

For the case 2), since 



Similarly, applying the fluid limit procedure and (6), we have:

Based on the analysis of the above two cases, we obtain that 

Theorem 2: The second stage crossbar and third stage VOQ operates under the above periodic permutation matrix are both rate stable.
Proof: The second stage crossbar always operates in work-conserving state and it behave as an OQ switch when the arrival traffic meet non-oversubscribed conditions. Therefore, 100% throughput is obtained in the second stage. More details can be found from Theorem 1 in [11]. In respect of the third stage, since the arrival traffic is already reshaped into unicast traffic, any MWM scheduling algorithm of VOQ can achieve 100% throughput under admissible unicast traffic.
4. Conclusion
This study proposes a novel 3-stage switch architecture composed of simple CICQ and VOQ switching fabric. A flexible and simple dedicated multicast scheduling algorithm M2U is designed for the first stage CICQ. 100% throughput can be achieved for integrated uni- and multicast traffic without speedup when cooperating with the proposed algorithm M2U in first stage and the simple periodic permutation matrix serials employed for the last two stages. The stable performance of the switching architecture is proved theoretically, therefore offering a promising choice for the scalability of high-speed IQ switches.
Acknowledgements
The authors would like to thank the NSFC 61271196 for supporting this work.
Cite this paper
Yan, F.L., Xiong, Q.X., Xiao, H. and Liang, J.C. (2017) Achie- ving 100% Throughput for Integrated Uni- and Multicast Traffic without Speedup. Int. J. Communications, Network and System Sciences, 10, 35-42. https://doi.org/10.4236/ijcns.2017.105B004
References
- 1. Wang, W.-F., Hung, L.-C. and Lu, C.-S. (2013) Design of Partially Buffered Crossbar Switches for Supporting Mixed Traffic. Ninth International Conference on Intelligent Information Hiding and Multimedia Signal Processing. https://doi.org/10.1109/iih-msp.2013.28
- 2. Gupta, S. and Aziz, A. (2002) Multicast Scheduling for Switches with Multiple In-put-Queues. Proceedings of the 10th Symposium on High Performance Interconnects. https://doi.org/10.1109/CONECT.2002.1039254
- 3. Bianco, A., et al. (2003) On the Number of Input Queues to Efficiently Support Multicast Traffic in Input Queued Switches. HPSR Workshop on High Performance Switching and Routing. https://doi.org/10.1109/HPSR.2003.1226689
- 4. Kyungmin, K., Seokhwan, K. and Jaiyong, L. (2013) Fanout Set Partition Scheme for QoS-Guaranteed Multicast Transmission. IEICE Transactions on Com- munications, 96, 3080-3090.
- 5. Koksal, C.E. (2008) On the Speedup Required to Achieve 100% Throughput for Multicast Over Crossbar Switches. 16th International Workshop on Quality of Service, IWQoS.
- 6. Giaccone, P. and Leonardi, E. (2008) Asymptotic Performance Limits of Switches with Buffered Crossbars Supporting Multicast Traffic. IEEE Transactions on Information Theory, 54, 595-607. https://doi.org/10.1109/TIT.2007.913564
- 7. Min, S. and Weiying, Z. (2004) Throughput Analysis for Multicast Switches with Multiple Input Queues. IEEE Communications Letters, 8, 479-481. https://doi.org/10.1109/LCOMM.2004.832733
- 8. Zhu, W. and Song, M. (2010) Performance Analysis of Large Multicast Packet Switches with Multiple Input Queues and Gathered Traffic. Computer Com- munications, 33, 803-815. https://doi.org/10.1016/j.comcom.2009.12.003
- 9. Ting, Z., Zhao, Y. and Wang, R. (2012) Achieving 100% Throughput in a Two-stage Multicast Switch. Journal of Electronics & Information Technology, 1, 82-88. (In Chinese)
- 10. Dai, J.G. and Prabhakar, B. (2000) The Throughput of Data Switches with and without Speedup. Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies. https://doi.org/10.1109/infcom.2000.832229
- 11. Chang, C.-S., Lee, D.-S. and Jou, Y.-S. (2002) Load Balanced Birkhoff-Von Neumann Switches, Part I: One-Stage Buffering. Computer Communications, 25, 611- 622. https:/doi.org/10.1016/S0140-3664(01)00427-3





