International Journal of Communications, Network and System Sciences
Vol.10 No.05(2017), Article ID:76530,11 pages
10.4236/ijcns.2017.105B003
A Highly Compatible Circular-Shifting Network for Partially Parallel QC-LDPC Decoder
Yanzhi Wang1, Zhenzhi Wu2, Peipei Liu1, Ning Guan1, Hua Wang1
1School of Information and Electronics, Beijing Institute of Technology, Beijing, China
2Center for Brain-Inspired Computing Research, Tsinghua University, Beijing, China



Received: March 2, 2017; Accepted: May 23, 2017; Published: May 26, 2017
ABSTRACT
The conventional methodology for designing QC-LDPC decoders is applied for fixed configurations used in wireless communication standards, and the supported largest expansion factor Z (the parallelism of the layered decoding) is a fixed number. In this paper, we study the circular-shifting network for decoding LDPC codes with arbitrary Z factor, especially for decoding large Z (Z  P) codes, where P is the decoder parallelism. By buffering the P-length slices from the memory, and assembling the shifted slices in a fixed routine, the P-parallelism shift network can process Z-parallelism circular-shifting tasks. The implementation results show that the proposed network for arbitrary sized data shifting consumes only one times of additional resource cost compared to the traditional solution for only maximum P sized data shifting, and achieves significant saving on area and routing complexity.
P) codes, where P is the decoder parallelism. By buffering the P-length slices from the memory, and assembling the shifted slices in a fixed routine, the P-parallelism shift network can process Z-parallelism circular-shifting tasks. The implementation results show that the proposed network for arbitrary sized data shifting consumes only one times of additional resource cost compared to the traditional solution for only maximum P sized data shifting, and achieves significant saving on area and routing complexity.
Keywords:
Partially Parallel Layered Decoding, Circular-Shifting Network, QC-LDPC Decoder, Arbitrary Expansion Factor

1. Introduction
Low-Density Parity-Check (LDPC) codes [1], firstly introduced by Gallager in 1960s, have been proved to approach the Shannon capacity. Structured LDPC codes such as quasi-cyclic LDPC (QC-LDPC) codes are widely used in wireless communication standards, such as IEEE 802.11n, IEEE 802.16e [2] for efficient hardware implementation.
Since the high computational complexity in the QC-LDPC decoder, the high- speed decoder often needs to accelerate decoding by using Application Specific Integrated Circuit (ASIC), these accelerators are difficult to modify after tape- out, therefore it is necessary to design the LDPC decoder with high flexibility. The variable parameters of QC-LDPC are mainly the base matrix Hb and the expansion factor Z. It is not difficult to compatible with arbitrary Hb that can be configured by memory. However, different Z (Maximum memory conflict-free parallel decoding sublayers) will lead to the adjustment of parallelism of the decoder. The decoder with parallelism P can easily support decoding QC-LDPC codes with Z ≤ P. Therefore previous schemes often apply a Z-parallelism as the hardware structure [3] [4] [5] in order to satisfy Z ≤ P. For the case of Z > P, several solutions are proposed in the literature review however have not be extended to support arbitrary Z. For example, Kuo et al. [6] proposed a shift network with 24 parallelism which is compatible for Z ≤ 96, but it is only considered for the Z parameters given in IEEE 802.16e. A method that uses multiple small parallel clusters and a uniform shift network to support large Z values was proposed in [7], however the proposed shift network is also tailored according to the maximum Z value. In this paper, we mainly study the circular-shift network with fixed P-parallelism compatible for arbitrary logic parallel sublayers of Z. The network receives P (called a group) from memory, and provides P output to the data path. When the current batch (in a cycle) of output originates from multiple batches of input, the shift network needs to buffer and splice the data. We study the cases in terms of different shift value, P and Z, and then we propose a Left-Right Shift Network (LRSN) architecture that basically based on a left shift network and a right shift network. The routing decision rules and the circuit architecture of the LRSN are presented. A simple data arrangement rules which enable the decoders to support all the Z larger than P is given, thereby the LRSN is suitable for any P-parallelism QC-LDPC decoders.
The remainder of this paper is organized as follows. Section 2 introduces the QC-LDPC codes employed in IEEE 802.11n and IEEE 802.16e, the architecture of the LRSN is proposed, and the principle of the LRSN is described in this section. The implementation results of the LRSN applied in the QC-LDPC decoder are demonstrated in Section 3. Finally, the conclusion is drawn in Section 4.
2. QC-LDPC and Partially Layered Decoder Shift Network Design
2.1. QC-LDPC and Partially Layered Decoder
For QC-LDPC codes, the sub-matrix size is defined by the expansion factor Z. The parity check matrix H of the QC-LDPC codes can be represented by the base matrix Hbmb×nb, where mb and nb are the sub-matrix number in a column and row respectively. As shown in Figure 1(a), each sub-matrix in the Hb is either the zero matrix or thecircular-shifted identity matrix. The H consists of a mb × nb array of Z × Z cyclically shifted identity matrices. The size of matrix H is M × N with M = mb × Z and N = nb × Z, where M is the number of parity check equations and N is the code length [8].
QC-LDPC decoders can be implemented efficiently using the layered decoding algorithm [6] [9], shown in Figure 1(a). From time step t = 0 to t = 6, the


Figure 1. Decoding scheduling comparison for fully parallel decoding and partially parallel decoding of QC-LDPC codes with expanding factor Z. (a) Fully parallel layered decoding flow; (b) Partially parallel layered decoding flow.
decoding is performed with the routine of one non-zero sub-matrix by another and layer by layer. In each step, Z messages within a submatrix are processed in parallel. The proposed partially layered decoding flow is shown in the Figure 1(b). Assume that Z = 3 × P, the Z messages in memory are placed in three rows with each row containing P messages. From t = 0 to t = 20, the decoder processes only P messages in each step. The corresponding decoder architecture of Figure 1(a) is shown in Figure 2(a), wherein Z messages are shifted then fed into the Z processing units. The updated messages are inverse shifted by the module in the dashed box, which can be discarded by a relative shifting method revealed in [6] [10]. Then the updated messages are written back to the memory. Compared to the traditional Z-parallelism solution, the proposed P-parallelism architecture is shown in Figure 2(b), wherein the Z messages are arranged in memory, and only P messages are fetched and shifted, then processed by the P processing units simultaneously. The P-parallelism shifter can support data shifting with any size Z (Z can be larger than P or Z is undecided). Figure 3 shows the comparison of shift output results of Z-sized and the P-sized shifter with Z = 56, P =

Figure 2. Comparison of decoder architectures between traditional fully parallel layered decoding and partially parallel layered decoding. (a) Z-parallelism; (b) P-parallelism.


Figure 3. The input and output of the circular-shift network with Z = 56 and r = 43. (a) Traditional network, P ≥ 56; (b) Proposed network, P = 24, wherein one row represents the output data for one clock.
24, and shift value r = 43, where the shadow parts are zeros. The LRSN receives P data, and outputs P shifted data with a valid flag. The LRSN is illustrated in detail in the next section.
2.2. Design of the Memory Subsystem and Circular-Shift Network
(a) Memory arrangement. For the LRSN, the Z data will be arranged as follows. Let L = [Z/P], where L denotes the number of P groups, and [*] represents the ceiling function. Let D represents the input data, and mem (x, y) is the arranged datum, mem (x, y) denotes the y-th number in row x, and the data are arranged following (1).
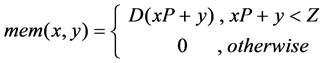 (1)
(1)
where x 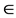 [0, L − 1], y
[0, L − 1], y 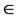 [0, P − 1].
[0, P − 1].
(b) Circular-shift network principles. The circular-shift network is responsible for circularly shifting the messages read from the memory into the correct order before they are processed by the processing units. The implementation of partially parallel LRSN is constrained by the following issues.
(1) Each group of output data may be derived from a number of memory units.
(2) A part of the output data from the shifter may output directly, whereas the others may need to be stored temporarily.
(3) Because the additional splicing and multiplexing logic are needed which consumes more propagation time, we enable the left-shifting and right-shifting networks working in parallel [11] for shortening the processing latency.
(4) Because in each clock P output data may originate from multiple memory units which cannot obtained in time, the no operation (NOP) clock needs to be inserted to pause the processing units. The experimental results show that the NOP clocks are less than 2 at most, so they are acceptable when Z is much larger than P.
The architecture of the left shift network is shown in Figure 4. The left shifter is based on a look-up-table. For the left shift network, DIn are the data fed into the shifter along with the shift value SV. The shifted data is in size 2P, where the remaining part of the shifted output is filled with zeros. Then the higher half of the shifted data are placed part in leftA and lower part are placed in leftB. The right shifter performs in opposite to the left shifter, and its output data are placed in rightA and rightB. The lower parts need to be one clock delayed for connecting with the higher parts of the subsequent shifted data, which are denoted by leftBd and rightBd, respectively. Due to uncertainty of Z and r, the final output Dout are selected partly from left part and partly from right part with several fixed rules in four cases. Hence a logic control state machine (LCSM)
Figure 4. The left shift network and data placement scheme.
with five states is introduced to represent these cases, as shown in Figure 5 and Figure 6.
(c) Detailed implementation. The memory accessing, shifting, and output multiplexing of LRSN are described as follows. Given that Z data are arranged in memory following (1).
(1) Calculate the memory access address which is defined as “addr”. Because the memory may be accessed by several times, the first group of data to be fetched is decided by the first output, which is calculated by addr <= [r/P], where [*] denotes the floor function. Then the “addr” updates following the Equation (2) in each clock, shown in Figure 8. The P data fetched from memory are sent to LRSN.
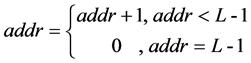 (2)
(2)
(2) Inside the LRSN, the shift value SV is calculated following (3).
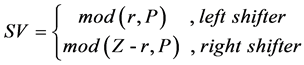 (3)
(3)
Especially, the SV of right shifter is P when r is an integer multiple of P.
(3) The routine for out1, out2, out3 and out4 follow (4) (5) (6) (7), where
Figure 5. The combination output of left and right shifter. The FSM is set as (1) S1: Dout is the combination of leftA and leftBd which from the left shifter. (2) S2: Dout is the combination of leftBd and leftA from the left shifter, and rightA from right shifter. (3) S3: combination of leftBd and rightA. (4) S4: combination of rightBd and rightA. (5) Idle: no operation.
Figure 6. State transition diagram of Logic Control State Machine for Dout source selection.
number “i” represents the index of the P data denoted by 0 to P − 1.
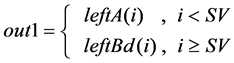 (4)
(4)
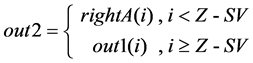 (5)
(5)
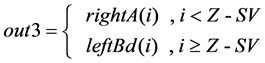 (6)
(6)
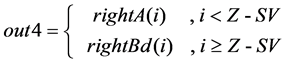 (7)
(7)
(4) The output data are always come from left shift network firstly and right shift network secondly. Therefore the four cases are transferred in a determined way shown in Figure 6. The upper left side of the dashed line indicates that the output of left shift network is used, otherwise the right shift network results are applied. A temporal flag LR is used for representing the output data are from the left shift network or not. The LR is initialized to 0 at start. We define “rtmp” as a variant initialized to r, and increases P per-clock when LR = 0.
The LCSM state transfers to S1 when the “start” is valid (a new sub-matrix is to be processed), and maintains at S1 state when addr < L − 1. The output may needs two input clocks of data, which are valid after one clock cycle, hence a NOP is issued firstly (output en = 0), then output selects Dout = out1.
The addr increases with clock. When reaching to the end of the current sub-matrix data, i.e., addr = L − 1, the output data are come from both the left shift and the right shift network, lasting for one clock. In this transition time, the case can be S2 or S3 in Figure 5, and whether leftA is required is determined by rtmp. If rtmp > Z, then the state transfers to S2. Since in S2, the data are from three memory units, so there will be a NOP cycle after S2 and the output data of left shift network (out1) needs to be maintained, then Dout = out2. Otherwise, if rtmp 
In the S4 state, the addr increases with clock until the numbers of output “en” reaches L which means all the Z-sized data are processed, and finally LCSM returns to Idle.
Figure 7 shows the architecture of the P-sized shift network, wherein DIn are the data from memory. The C(i) is defined as follows: if i < SV , then C(i) = 1, else C(i) = 0, where i from 0 to P − 1. The C(i) controls the P multiplexers to generate out1, out2, out3 and out4.
(d) Representative example. Figure 8 shows the shift operation process of the example we mentioned in Figure 3 with Z = 56, P = 24, r = 43. Where the “en” and “out addr” are the shifted data output enable and address, respectively. When t = 0, the data from memory address addr = [43/24] = 1 are sent to the left shifter, and shift value is SV = mod(r, P) = 19. The LCSM is in S1 and rtmp = 43.
Figure 7. Top-level architecture of the proposed circular-shift network. The Dout selects from four alternatives which is shown in Figure 5.
Figure 8. Shift operation process of Z = 56, P = 24, r = 43.
When t = 1, the data from addr = 2 are sent to the left shifter, and shift value is 19. Since addr = 2 and rtmp = 67 > 56, so the LCSM transfers to S2. When t = 2, the data from addr = 0 are sent to the right shifter, and shift value is mod (Z ? r, P) = 13, then Dout = out2, the LCSM transfers to S4. The shift operation is completed when the numbers of output “en” reaches 3. Finally, the LCSM returns to Idle.
3. Implementation Results
We implemented the LRSN in a Xilinx Kintex7 xc7k325T FPGA chip. Reference [4] designed a Zmax circular-shifting network to support all Z configurations less than Zmax, which has simpler routing decision and less complexity than the other Zmax networks. So, we re-imple- mented the shift networks with P = 24, 96, 128, 360 and 512, and compared them to the proposed LRSN in this paper. We compare them with Slice Registers, Slice LUTs, LUT Flip Flop and Z compatibility. For a fair comparison, the messages are quantized by 6 bits.
The results are shown in Figure 9. The resources consumption are increasing in linear along with Z increases using the solution in [4]. In addition, there will be much time in synthesis and hard to place and route in chip while Z is large in LDPC decoder. On the contrary, we achieve a unified circular-shifting architecture for any Z number with fixed resources consumption. The additional resource cost is only one times more than the corresponding network with Z configurations proposed in paper [4] (such as Z = 24). By this additional cost, the proposed network enables a compatibility for IEEE 802.11n, IEEE 802.16e and DVB-S2 and other QC-LDPC codes with flexible Z on a P-parallelism hardware. In addition, the proposed solution may introduce additional NOPs due to the memory data un-alignment, such as the output of data may originated from two or three memory banks which needs more cycles to access, shown in Figure 8. The analysis of the ratio of the NOP clock numbers and processing clock numbers at different P and Z as shown in Figure 10. Comparison with P = 8, 12, 24, we can obtain that the NOP clock occupancy is less than 10% when Z/P > 20 (large Z case). The additional cost would be less than 50% for small Z case. When Z ≤ P, the proposed LRSN has the same timing flow and no pipeline stall is needed.
4. Conclusion
We presented a fixed complexity highly compatible circular-shifting network called LRSN with time-sharing capability for partially layered LDPC decoder. The LRSN employs fixed routine and memory mapping to support partially parallel layered decoding of LDPC with any expansion factor. When the memory capacity is guaranteed, the LRSN can be used to decode LDPC codes with long block sizes, so the compatibility of the decoder is enhanced. In addition, the proposed LRSN can be applied for reducing the hardware cost by introducing a
Figure 9. The resources consumption comparison of different shift networks.
Figure 10. NOP clock occupancy in different shift networks.
much lower hardware parallelism, when the data rate are not quite high such as in DVB-S2 and DVB-T standards.
Acknowledgments
This work is supported by “National High Technology Research and Development Program of China” (Grant No. 2015AA01A709) and “National Science Foundation of China (NSFC)” (Grant No: 61471037).
Cite this paper
Wang, Y.Z., Wu, Z.Z., Liu, P.P., Guan, N. and Wang H. (2017) A Highly Compatible Circular- Shifting Network for Partially Parallel QC-LDPC Decoder. Int. J. Communications, Network and System Sciences, 10, 24-34. https://doi.org/10.4236/ijcns.2017.105B003
References
- 1. Gallager, R. (1962) Low-Density Parity-Check Codes. IEEE Trans. Inf. Theory, IT-8, 21-28. https://doi.org/10.1109/TIT.1962.1057683
- 2. Fossorier, M.P.C. (2004) Quasicyclic Low-Density Parity-Check Codes from Circu-lant Permutation Matrices. IEEE Trans. Inf. Theory, 50, 1788-1793. https://doi.org/10.1109/TIT.2004.831841
- 3. Liu, C.H., Yen, S.W., Chen, C.L., Chang, H.C., Lee, C.Y., Hsu, Y.S. and Jou, S.J. (2008) An LDPC Decoder Chip Based on Self-Routing Network for IEEE 802.16e Applications. EEE J. Solid-State Circuits, 41, 684-694. https://doi.org/10.1109/JSSC.2007.916610
- 4. Liu, C.H., et al. (2009) Design of a Multimode QC-LDPC Decoder Based on Shift-Routing Network. IEEE Transactions on Circuits and Systems II: Express Briefs, 56, 734-738. https://doi.org/10.1109/TCSII.2009.2027967
- 5. Rovini, M., Gentile, G. and Fanucci, L. (2007) Mulit-Size Circular Shifting Net-works for Decoders of Structured LDPC Codes. Electronics Letters, 43, 938- 940. https://doi.org/10.1049/el:20071157
- 6. Kuo, T.-C. and Willson, A.N. (2008) A Flexible Decoder IC for WiMAX QC-LDPC Codes. Custom Integrated Circuits Conference, CICC 2008, San Jose, CA, 527-530.
- 7. Rovini, M., Gentile, G., Rossi, F. and Fanucci, L. (2007) A Scalable Decoder Architecture for IEEE 802.11n LDPC Codes. Global Telecommunications Conference, GLOBECOM’07, Washington DC, 3270- 3274. https://doi.org/10.1109/glocom.2007.620
- 8. Wang, Z. and Cui, Z. (2007) Low-Complexity High-Speed Decoder Design for Qua-si-Cyclic LDPC Codes. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 15, 104-114. https://doi.org/10.1109/TVLSI.2007.891098
- 9. Sun, Y. and Cavallaro, J.R. (2013) VLSI Architecture for Layered Decoding of QC-LDPC Codes With High Circulant Weight. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 21, 1960-1964. https://doi.org/10.1109/TVLSI.2012.2220388
- 10. Brack, T., Alles, M., Kienle, F. and Wehn, N. (2006) A Synthesizable IP Core for WIMAX 802.16E LDPC Code Decoding. 2006 IEEE 17th International Symposium on Personal, Indoor and Mobile Radio Commu-nications, Helsinki, 1-5. https://doi.org/10.1109/PIMRC.2006.254126
- 11. Chen, X.H., Lin, S. and Akella, V. (2010) QSN—A Simple Circular-Shift Network for Reconfigurable Quasi-Cyclic LDPC Decoders. IEEE Transactions on Circuits & Systems II Express Briefs, 57, 782-786. https://doi.org/10.1109/TCSII.2010.2067811








