J. Biomedical Science and Engineering, 2011, 4, 569-582 JBiSE
doi:10.4236/jbise.2011.49073 Published Online September 2011 (http://www.SciRP.org/journal/jbise/).
Published Online September 2011 in SciRes. http://www.scirp.org/journal/JBiSE
Generalized electro-biothermo-fluidic and dynamical
modeling of cancer growth: state-feedback controlled
cesium therapy approach
Murad Al-Shibli
College Requirement Unit, Abu Dhabi Polytechnic, Institute of Applied Technology, Abu Dhabi, United Arab Emirates.
Received 21 December 2010; revised 23 February 2011; accepted 5 July 2011.
ABSTRACT
This paper develops a generalized dynamical model
to describe the interactive dynamics between normal
cells, tumor cells, immune cells, drug therapy, elec-
tromagnetic field of the human cells, extracellular
heat and fluid transfer, and intercellular fractional
mass of Oxygen, cell acidity and Pancreatin enzyme.
The overall dynamics stability, controllability and
observability have been investigated. Moreover, Ce-
sium therapy is considered as a control input to the
11-dimensional dynamics using state-feedback con-
trolled system and pole placement technique. This
approach is found to be effective in driving the de-
sired rate of tumor cell kill and converging the sys-
tem to healthy equilibrium state. Furthermore, the
ranges of the system dynamics parameters which
lead to instability and growth of tumor cells have
been identified. Finally, simulation results are
demonstrated to verify the effectiveness of the ap-
plied approach which can be implemented success-
fully to cancer patients.
Keywords: Cancer; Tumor Growth; Tumor Dynamics
and Modeling; Immune System; Cesium Therapy;
State-Feedback Control; Pole Placement
1. INTRODUCTION
There are over 200 different types of cancer that affect
virtually every organ in the body. They can seem bewil-
deringly different but all cancers share certain features as
outlined by Douglas Hanahan and Robert Weinberg [1].
Six essential alterations in cell physiology that collec-
tively dictate malignant growth: self-sufficiency in
growth signals, insensitivity to antigrowth signals, eva-
sion of programmed cell death (apoptosis), limitless rep-
licative potential, sustained angiogenesis, and tissue in-
vasion and metastasi.
The technical report [2] presents what is known today
concerning non-ionizing electromagnetic field interac-
tion with the human body. Many significant and inter-
esting effects are identified. As an example, both theo-
ries and observations link non-ionizing electromagnetic
field to cancer in humans, in at least three different ways:
as a cause, as a means of detection and as an effective
treatment.
A phase-space analysis of a mathematical model of
tumor growth with an immune response and chemother-
apy is introduced in [3]. It is proved that all orbits and
trajectories are bounded and converge to one of several
possible equilibrium points. The addition of a drug to the
system can move the solution trajectory into a desirable
basin of attraction.
State Dependent Riccati Equation (SDRE) based op-
timal control technique to a nonlinear tumor growth
model is applied in [4]. The model consists of three bio-
logical cells which are normal tissue, tumor and immune
cells. The effect of chemotherapy treatment is also in-
cluded in the model. Chemotherapy administration is
considered as a control input to the nonlinear cancer
dynamics and the amount of administered drug is deter-
mined by using SDRE optimal control. The optimal con-
trol is applied to the model in order not only to drive the
tumor cells to the healthy equilibrium state but also to
minimize the amount of the drug used.
A basic mathematical model of the immune response
when cancer cells are recognized is proposed. The model
consists of six ordinary differential equations [5]. It is
extended by taking into account two types of immuno-
therapy: active immunotherapy and adoptive immuno-
therapy. An analysis of the corresponding models is
made to answer the question which of the presented
methods of immunotherapy is better.
Review [6] explains why mathematics is a powerful
tool for interpreting such data by presenting case studies
that illustrate the types of insight that realistic theoretical

M. Al-Shibli / J. Biomedical Science and Engineering 4 (2011) 569-582
570
models of solid tumour growth may yield. These range
from discriminating between competing hypotheses for
the formation of collagenous capsules associated with
benign tumours to predicting the most likely stimulus for
protease production in early breast cancer.
Understanding the dynamics of human hosts and tu-
mors is of critical importance [7]. A mathematical model
was developed that explored the immune response to
tumors that was used to study a special type of treatment.
This treatment approach uses elements of the host to
boost its immune response in the hopes that the host can
clear the tumor.
Two models of optimizing tumor growth are presented
in [8] In the first model optimal controls minimize the
tumor volume for a given amount of angiogenic inhibi-
tors to be administered while the second formulation
tries to achieve a balance between tumor reduction and
total amount of angiogenic inhibitors given. For both
models a full synthesis of optimal solutions determined
by portions of bang and singular controls with rest peri-
ods is presented. The differences in the two solutions are
discussed.
A new mathematical model is developed for the dy-
namics between tumor cells, normal cells, immune cells,
chemotherapy drug concentration and drug toxicity [9].
Then, the theorem of Lyapunov stability is applied to
design treatment strategies for drug protocols that ensure
a desired rate of tumor cell kill and push the system to
the area with smaller tumor cells.
Cells, whether cancerous or normal can only live and
reproduce (undergo mitosis) in a pH range of between
6.5 and 7.5. A healthy cell has a pH of 7.35 while a can-
cer cell is more acidic. When the pH of a cancer cell
goes above 7.5 it dies and if it goes above 8.0 it will die
in a matter of hours.
Every cell in the body works as milli-volt battery. To
successfully bring nourishment in, and take poisons out,
it has to be fully charged. In a cancerous cell, the cell
voltage drops from 90 millivolts to less than 40 milli-
volts. When the cell voltage gets to the very bottom,
only 5 substances can pass in or out of the cell. They are
water, sugar, potassium, cesium and rubidium. Oxygen
cannot enter into a cancer cell. Even if there is a lot of
oxygen in the blood, it won’t get into the cell.
Potassium ions are responsible for the ability of glu-
cose to enter the cell. Potassium enters cancer cells in a
normal manner so glucose still enters the cancer cell.
Cancer cells have only 1% of the calcium content found
in normal healthy cells. The calcium, magnesium and
sodium ions, which are responsible for the intake of ox-
ygen into the cell, cannot enter the cancer cell but the
potassium ion still enters these cells. Thus we have can-
cer cells containing glucose but no oxygen.
A healthy individual has a blood oxygen level of be-
tween 98 and 100 as measured by a pulse oximeter. No-
bel Prize Laureate, Dr. Otto Warburg, discovered that
when he lowered the oxygen levels of tissues by 35 %
for 48 hours normal cells were converted into irreversi-
ble cancer cells [10]. Cancer patients have low levels of
oxygen in their blood usually around 60 compared to
normal values of about 100 by pulse oximetry. The
common therapies used to treat cancer (chemotherapy
and radiation) both cause drastic falls in the body's oxy-
gen levels. Tissues that are acidotic contain low levels of
oxygen whereas tissues that are alkalotic have high lev-
els of oxygen.
When oxygen fails to enter the cell the cell's ability to
control, its pH is lost and the cell becomes quite acidic.
This is caused by the appearance of abnormal metabo-
lism (anerobic glycolysis) in which glucose is converted
(fermentation) into two particles of lactic acid. This
production of lactic acid promptly lowers the ph within
the cell to 6.5 or lower. The lactic acid damages the tem-
plate for proper DNA formation. Messenger RNA is also
changed so the ability of the cell to control its growth is
lacking. Rapid and uncontrolled cancer cell growth and
division occurs. Vitamin C and zinc are able to enhance
the uptake of cesium, rubidium, and potassium into can-
cer cells.
Cancer cells develop a protein coating 13 times thick-
er than normal cells. This makes it difficult for the im-
mune system to attack them. By ingesting high doses
of pancreatin, you can actually dissolve cancer cells
inside the body [11]. In the natural course of one’s life-
time, millions of cancer cells develop, and are harmless-
ly digested by the immune system. The body uses pan-
creatin, a secretion from the pancreas to dissolve the
cancer cells. As we age, the pancreas is less and less able
to make this important substance. By taking pancreatin
orally, it is possible to increase the levels of its active
ingredients in the blood, thereby helping the body break
down the cancer cells and remove them from circulation.
The active ingredients in pancreatin which have shown
to have tumor dissolving abilities are trypsin and chy-
motrypsin. These ingredients were taken out of virtually
all the pancreatin supplements available to consumers
years ago. These active ingredients are being bought in
massive quantities by the sewerage industries to digest
the sewerage into less noxious forms.
Although many improvements and mathematical
modeling have been introduced in the treatment of can-
cer, but majority has been limited to of modeling of
normal cells, tumor cells, immune cells and cancer ther-
apy and toxicity effects. Moreover, development of
treatment strategies requires many clinical experiments
first on animals and then on humans in order to figure

M. Al-Shibli / J. Biomedical Science and Engineering 4 (2011) 569-582
571
out a convenient way for the administration of the ther-
apy. These experiments, in general, take a long time and
most importantly may result in many deaths during the
development period. Clinical experiments also reveal the
fact that there is a strong relationship between the cancer
state (the number and/or volume of tumor cells, tumor
type), the immune system of the patient and the treat-
ment strategy. Hence, understanding the dynamical be-
havior of cancer has received a great interest.
This paper develops a generalized dynamical model to
describe the interactive dynamics between normal cells,
tumor cells, immune cells, drug therapy, electromagnetic
field of the human cell, extracellular heat and fluid
transfer, and intercellular fractional mass of oxygen, cell
acidity and pancreatin. The overall dynamics stability
and controllability has been investigated. Moreover, Ce-
sium therapy is considered as a control input to the
11-dimensional dynamics using state-feedback con-
trolled system and pole placement technique. This ap-
proach is found to be effective in driving the desired rate
of tumor cell kill and converging the system to healthy
equilibrium state. Furthermore, the ranges of the system
dynamics parameters which lead to instability and
growth of tumor cells have been identified. Finally, sim-
ulation results are demonstrated to verify the effective-
ness of the applied approach which can be implemented
for each individual case.
This paper is organized as follows. Section 2 intro-
duces modeling of the electromagnetic field of a live cell,
cellular heat and fluid transfer are presented in Sections
3 and 4, respectively. Cellular factional composition is
outlined in Section 5, generalized cellular-tumor dy-
namics is detailed in Section 6. Controllability and
state-feedback control design of tumor dynamics are
presented in Section 7. Section 8 demonstrates simula-
tion which followed finally conclusions.
2. ELECTROMAGNETIC CELLULAR
MODELING
A great variety of theories have been developed to de-
scribe the electro-magnetic field of the human body.
Some theories regarded the human body as a whole as
single prolate spheroid with a single set of electromag-
netic constants: permittivity, permeability, and conduc-
tivity [2].
In that sense, the body is a simple antenna or probe
capable o f intercepting a certain amount of electromag-
netic energy, which is converted entirely in to heat. At
the other extreme, the body may be regarded as a collec-
tion of countless electronic microcircuits, each one cor-
responding to an individual cell or partially. Electro-
magnetic energy somehow finds its way to individual
microcircuits and influences the electronic functions
there. These functions include various communication
and control processes essential to life and its activities.
Efforts to understand these have focused attention on the
microscopic components of the tissues such cells, mem-
branes, fluids, molecules in solution rather than the tis-
sue taken as a whole. Some theories have been devel-
oped concerning individual cells. An equivalent circuit
has been developed as shown below. Given an incident
current or current density actually passing across the cell
membrane through and through the cell can be calculat-
ed. If the current is sufficiently enough, different re-
sponses are possible. For example a current density of 1
mA/cm2 is about the amount associated with the action
potential of nerve and muscle cells. Perhaps a pulsed
electromagnetic filed could simulate these action poten-
tials and confuse the body by generating false signals.
Of the cells part, the membrane probably has attracted
most attention at least with respect top electromagnetic
effects. Many membrane properties have been quantified.
Typical thickness 45 Ang, typical capacitance 1 micro-
farad/cm2, typical leakage conductance 1 - 10 mhos/cm2,
typical resting potential 100 millivolts, dielectric con-
stant 5, Electric field 22 Million V/m, Surface charge
density 9.7 × e–8 C/cm2 = 6.1 × e11 charge/cm2. Of these
perhaps the electric filed is the most remarkable one
since it is almost greater than any other found in nature.
For example the electric field of the Earth at its surface
is only about 100 V/m.
So far the membrane has been treated as a homoge-
nous substance and characterized by a capacitance and
nonlinear conductance. In fact the membrane is not ho-
mogenous. The basic structure is a double layer of mol-
ecules called lipids. Lipids are hydrophobic, that is, they
repel water. It is the repulsion that holds the membrane
together. Proteins are chains of mino-acids. Proteins are
so important because they can conduct charges while
lipids are good insulators. Thus proteins are the con-
ductance in the electronic circuit of the membrane.
Electromagnetic field can interact with proteins over a
wide range of frequencies between 1 - 10 MHz. It de-
pends on its size and mass protein can be modeled as
single dipole which rotates in response to an oscillating
field.
Proteins figure predominantly in at least one of the
theories of cancer advanced by Nobel Laureate Albert
Szent-Gyorgyi which currently being researched [2,10].
According to this theory, proteins conduct electron out
of the cell interior. Oxygen molecules at the cell exterior
accept the electrons and carry them away. These free
electrons are the products of some chemical process in-
side the cell that inhibits reproduction. If the electrons
are not conducted away, then the process stops, and the
cell divides at uncontrollable rate. Eventually, there are

M. Al-Shibli / J. Biomedical Science and Engineering 4 (2011) 569-582
572
enough cells to form a tumor which characterized by
poorly circulated system. So, little or no oxygen-carrying
blood reaches the cells.
The equivalent impedance (resistance)
eq
Z
of the
equivalent electric circuit of the human cell can now be
expressed in the Laplace domain as:
 
2
2
22
i ewe
eq
iewi we we e
R RCsR
ZRR CsRCR CR Cs


(1)
where
i
R
is the intracellular medium resistance,
e
R
is
the extracellular medium resistance,
w
C
is the capaci-
tance of the cell wall,
e
C
is the capacitance of extra-
cellular medium.
Now it is possible to express the voltage across the
cell
()Vs
using Ohm’s law such that
()
() eq
Vs Z
Is 
(2)
where the
()Is
is the passing cellular current.
The voltage-current time change can be formulated by
taking the Laplace inverse of the former equation as fol-
lows (assuming zero initial conditions)
 
( )2( )2()
( )2( )
iewi we we e
i e we
RR CVtRCR CR CVtVt
RRCI tRIt


(3)
The right hand side of the last Eq.3 represents the in-
put source to the cell. Since
e
R
represents the extra-
cellular resistance then the term
( )()
ee
R ItVt
is the
external voltage source to the cell and the term
( )( )
e ex
R ItVt
the rate of change of the external voltage
source. The equation now can be modified to
 
( )2( )2()
( )2( )( )
iewi we we e
iw exexe
RR CVtRCR CR CVtVt
RCV tV tut

 
(4)
Figure 1. Passage of electric current I in the human cell and its
/equivalent electric circuit.
e
R
is the extracellular resistance,
i
R
is the intracellular resistance,
w
C
is the capacitance of
the wall of the cell and
e
C
is the extracellular capacitance.
Eq.4 It represents an input-output relationship of the
electric behavior of the cell in a second order ordinary
linear differential equation form. Next section will in-
troduce the dynamics of extracellular heat transfer as it
is so important to maintain steady-state heat from and
into the human cells.
3. EXTRACELLULAR HEAT TRANSFER
Thermal system involves transfer of heat from one cell
to another. It may be analyzed I terms of thermal re-
sistance and capacitance. To simplify the analysis it is
assumed that the cellular thermal system can be repre-
sented by a lumped-parameter model, that substances
that are characterized by resistance to heat flow have
negligible heat capacitance, and that substances that are
characterized by heat capacitance have negligible re-
sistance to heat flow. Conduction and convection heat
flow is only considered.
For conduction or convection heat transfer,
qK  
(5)
where
q
is the heat flow rate (kcal/sec),
 
is the
temperature difference (˚C) and
K
is the heat coeffi-
cient (kcal/sec.˚C). The coefficient
K
is given by
/K kAx
for conduction and
K HA
for convec-
tion, where
k
is thermal conductivity kcal/m.sec.˚C,
A
is the area normal to heat flow m2,
x
is the
thickness of the conductor (m) and
H
is the convec-
tion coefficient (
2
kcal/m .sec.
˚C).
Thermal resistance for heat transfer between two cells
may be defined as
Change in Tepmerature Difference C
Change in Heat Flow Ratekcal/sec



h
R
The thermal resistance for conduction or convection
heat transfer is given by
( )1
hd
Rdq K
 

(6)
The thermal capacitance
Change in Heat Stored
Change in TemperatureC




hh
kcal
Cm c
where
m
is mass of the cell considered (kg), and
c
is
the specific heat of the cell
kcal/ kg.C
.
It is desired now to conisder the tmprature change of a
human cell such that fluid inside the cell is perfectly
mixed such that the cell temprature is homogenoues. A
single temprature is considred the intracellular tem-
prature and the outflowing fluid.
The diffrential equation for the system is now
hin out
d
Cq q
dt


(7)
where

M. Al-Shibli / J. Biomedical Science and Engineering 4 (2011) 569-582
573
1()
out out
qR  
(8)
Combing the last two Eqs.7-8 yields
hhh inout
R CR q    
(9)
It now possible now to express the generated cellular
entropy
S
by
q
S


. Eq.9 shows that the temperature
of the cell is changing as first order diffrentail dynamics
given a heat input source and heat losses to the sur-
rounding. Next section will consider how water flow in
the cell changes.
3. INTRACELLULAR FLUID MODELING
Consider now the flow between two adjacent cells
through their walls. The flow resistance for liquid flow
through the cellular walls is defined as the change in the
level difference necessary to cause a unit change in flow
rate, that is
3
Change in Level Differencem
Change in Flow Ratem /sec



f
R
It is assumed that the flow is laminar. The relationship
between the steady-state flow and steady-state head is
defined as
QK h
(10)
where
Q
is the steady-state flow rate(
3
m /sec
),
K
is
flow coefficient (
2
m /sec
), and
h
is the steady-state
head (
m
).
The capacitance
C
of a tank is defined to be the
change in quantity of stored fluid necessary to cause a
unit change in the potential head.
3
Change in Lquid Storedm
Change in Headm



f
C
Since the inflow minus the outflow during a small
time interval
dt
is equal to the additional amount
stored in the cell, then
()
fin out
C dhQQdt
(11)
From the definition of the flow resistance, the rela-
tionship between
out
Q
and
h
is given by
/
out h
Qh R
(12)
The differential equation for the fluidic system now
becomes
fff in
R ChhR Q
(13)
The former equation is a first order differential dy-
namical system show how the water content level is
changing inside the cell given a regular water inflow.
Such a dynamics can be useful in modeling the fraction-
al mass of substances inside the human cell. Oxygen,
and hydrogen ions and Pancreatin are considered in this
paper for their major role in keeping healthy cells and
killing the tumor cells or at least stopping their growth.
4. CELLULAR COMPOSITION
DYNAMICS
To determine the properties of a mixture, we need to
know the composition of the mixture as well as the
properties of the individual components. There are two
ways to describe the composition of a mixture: either by
specifying the number of moles of each component,
called molar analysis, or by specifying the mass of each
component, called gravimetric analysis.
Consider a fluid mixture composed of
n
compo-
nents. The mass of the mixture
T
m
is the sum of the
masses of the individual components, and the mole
number of the mixture
T
N
is the sum of the mole
numbers of the individual components
1
n
Ti
mm
and
1
n
Ti
NN
(14)
The ratio of the mass of a component to the mass of
the mixture is called the mass fraction
i
x
, and the ratio
of the mole number of a component to the mole number
of the mixture is called the mole fraction
i
y
:
i
iT
m
xm 
and
i
iT
m
ym 
(15)
We can easily show that the sum of the mass fractions
or mole fractions for a mixture is equal to 1
11
n
i
x

and
11
n
i
y

(16)
It is assumed that the intercellular mixture is homo g-
enous such that it is possible to express the he ratio of
the mass of each substance with respect to the water
volume as follows (substance-water ratio):
imm
vV Ah 
(17)
where
i
v
is the substance mass ration in a unit volume
of water exists in the cell, mass m of a substance,
V
is
the water volume,
A
is the average cross sectional area
of the cell, and
h
is the water head indicator. The mass
m
of a substance is related to the number of moles
N
through the relation
m NM
, where
M
is the molar
mass.
The former Eq.17 can now be modified to
i
mvAh
(18)
The rate of change of each individual substance mass
in the cellular fluid can be expressed as

M. Al-Shibli / J. Biomedical Science and Engineering 4 (2011) 569-582
574
iii
mv Ahv Ahv Ah 
(19)
Next section will outline how this equation can be
used to represent the contents of oxygen, hydrogen ions
(as a measure of PH) and Pancreatin enzyme as a killer
for the tumor cells.
5. GENERALIZED
ELECTRO-BIO-THERMAL TUMOR
DYNAMICS
Mathematical models for cancer dynamics have been
studied by many scientists using different mathematical
methods. Some of these models consider the growth of
tumor cells as population dynamics problems which in-
clude the interaction of tumor cells with other cells (e.g.
normal cells and immune cells). In order to develop
treatment strategies, the effects of therapy are also in-
cluded in the models as control inputs. In this study, we
analyze the model originally discussed in [4]. The model
does not aim to concentrate on a specific kind of cancer
and uses normalized parameters. It includes three dif-
ferent cell populations and chemotherapy drug concen-
tration. Interaction of the tumor cells with normal and
immune cell population in the absence of any treatment
is given by the system
1111 11 12
(1 )xrxbxcxx 
(20)
22 2222 123 2 3
(1 )xrxbxcxxcxx 
(21)
23
304231 3
2
xx
xsc x xdx
x
  

(22)
where
1()xt
,
2()xt
and
3()xt
denote the number of
normal cells, the number of tumor cells and the number
of immune cells at time t , respectively. The first term in
the normal cell population is the logistic growth of nor-
mal cell population with growth rate
1
r
and maximum
carrying capacity
1
(1/ )b
. The second term is the loss of
normal cells due to competition among tumor-normal
cells for local resources. In a tumor cell population, the
first term denotes the logistic growth of tumor cells in
the absence of immune surveillance with the growth rate
2
r
and maximum tumor carrying capacity
2
(1/ )b
.
The second and the third terms in (24) are death terms
for tumor cells due to the interaction between immune
and normal cells, respectively. Immune cells have a con-
stant source
0
s
which can be supplied from bone mar-
row or lymph nodes. In the presence of tumor cells, im-
mune cells are stimulated by tumor cells with a Michae-
lis-Menten type saturation function with the positive
parameters

and

. Immune cells are deactivated
by tumor cells at the rate
4
c
and they also die at the
natural death rate
1
d
.
There are different ways to include the effect of
chemotherapy in the tumor growth model. We assume
that chemotherapy kills all cell populations with differ-
ent ratios using mass action term. The effect of drug
therapy in the model is shown with an additional state
4()xt
and control input
()ut
which denote drug con-
centration in the blood stream, and external drug injec-
tion respectively. The nonlinear system (20)-(22) with
the effect of drug therapy is:
1111 11 121 14
(1 )xrxb xc x xa x x 
(23)
22 22 221232 32 2 4
(1 )xrxbxc xxcx xa x x 
(24)
23
304 2 31 32 3 4
2
xx
xsc x xdxa xx
x
  

(25)
42 4()xdxut 
(26)
Here,
1
a
,
2
a
, and
3
a
are the different killing ef-
fects of chemotherapy on the cell populations. Chemo-
therapy drug decay rate in the blood stream is denoted
by
2
d
. The system parameters which are normalized to
the maximum carrying capacity of the normal cells are
given in Table 1. Analysis of the model for possible
equilibrium points in the absence of therapy is given in
the next sub-section.
In order now to generalize the dynamics of the cell in
terms of electromagnetic model, heat transfer model,
fluid transfer model, fractional mass model, cellular
growth, let us introduce the state space dynamic vari-
ables as follows.
Define the electric charge passing from or into the call
()Vt
as
5
x
. Since the electric current flow is the rate
of change of charge passing through an inductor
Iq
then
56 ()xxV t
(27)
6()xVt
(28)
Then the equivalent electric circuit Eq.4 can be re-
expressed as
 
66 5
( )2( )2( )
( )2( )( )
iewi we we e
iw exexe
RR CxtRCR CR Cxtxt
RCV tV tut

 
(29)
The electric dynamics (29) can be modified as
 
66
5
2
2()
iwe we e
i e w
e
i e w
RCR CR C
xx
R R C
xu t
R R C



(30)
Furthermore, representing the heat model (9) in the
state space form assuming
7
x  
yields
77
1h inout
hh
xxR q
RC
  
(31)

M. Al-Shibli / J. Biomedical Science and Engineering 4 (2011) 569-582
575
Table 1. Overall dynamics parameters.
Parameter
Value
1
r
1
2
r
1.5
1
b
1
2
b
1
1
c
1
2
c
0.5
3
c
1
4
c
1
1
a
1
2
a
0.15
3
a
0.05
1
d
0.2
2
d
1
0
s
0.33

0.1

0.3
i
R
5
12 10
e
R
5
1 10
W
C
6
1 10 
e
C
6
1 10 
h
R
1/ 0.026
h
C
1700
f
R
6
1 10
f
C
1600
A
1
2
O

0.75
H


0.02
Pn

0.05
A

1.9
2
O

0.21
H


0.01
Pn

0.003
Similarly, for the cellular fluid transfer (13) assuming
8
xh
will lead to
88
1in
ff
xx Q
RC
 
(32)
For the significant of the oxygen, pH and Pancreatin
enzyme for the survival of the normal cell, their frac-
tional mass ratio will be considered. Denote their corre-
sponding masses, respectively, as
9oxygene
xm
,
10 H
xm


and
11 Pancreatin
xm
(33)
Referring to (18) and (19), last Eq.33 can be reformu-
lated as
 
i
i
iiiivA ii
i
vA
mmmv Ahmv Ah
vA
  
(34)
By the virtue of the fluid dynamics equation the for-
mer equation the fractional mass of the oxygen, pH and
Pancreatin enzyme can be described, respectively, by
 
2
22
9 89
O
OAO in
ff
vA
xxxv AQ
RC
  
(35)
 
10 810
HA in
HH
ff
vA
xxxv AQ
RC



 
(36)
 
11 811
Pn PnAPn in
ff
vA
xxxv AQ
RC
  
(37)
where
2
O
v
,
H
v
and
Pn
v
are the fractional ratios of
oxygen, hydrogen as a measure of PH and Pancreatin,
respectively. Fractional rate of change of the three sub-
stances with respect to their initial values are defined,
respectively, as
2
2
2
O
OO
v
v
 
,
H
HH
v
v





and
pn
Pn Pn
v
v
 
along with the rate of change of the cell surface area
with respect to its initial value as
A
A
A
 
. Selection of
such substances are based on their significant role in the
survival of human cell and killing or at least slowing
down the tumor cells.
Now the overall generalized model is
11 11 11 12114
(1 )xrxbxc x xa x x 
(38)
22 22221232 32 2 4
(1 )xrxbxc xxcx xa x x 
(39)
23
304 2 3132 3 4
2
xx
xsc x xdxa xx
x
  

(40)
42 4()xdxu t
(41)
56
xx
(42)
 
66
5
2
2()
iwe we e
i e w
e
i e w
RCR CR C
xx
R R C
xu t
R R C



(43)
77
1h inout
hh
xxR q
RC
  
(44)
88
1in
ff
xx Q
RC
 
(45)
 
2
22
9 89
O
OAO in
ff
vA
xxxv AQ
RC
  
(46)

M. Al-Shibli / J. Biomedical Science and Engineering 4 (2011) 569-582
576
 
10 810
,
HA in
v HH
ff
vA
xxxv AQ
RC



 
(47)
 
118 ,11
Pn v PnAPnin
ff
vA
xxxv AQ
RC
  
(48)
The overall generalized dynamics represents the bio-
thermal electro-fluidic dynamics with 11 dimension.
Next section will investigate the stability of the entire
dynamical system at equilibrium points.
5.1. Equilibrium State
It is necessary to investigate the equilibrium state of the
cell since it indicates its stability and the non-growth of
the tumor cells. As a start, let us assume a free therapy
and find out the corresponding equilibrium points for the
dynamics (38)-(41).
As for the normal cells, equilibrium is governed by
11 1111 12
(1 )0xrxb xc x x 
indicates that
1211 11211
0,(1)/, and when 1/xxrbxcxxb 
Tumor cells equilibrium exists when
22 2222123 2 3
(1 )0xrxbxc xxcx x 
(49)
at points satisfy
22222 2132 23
0 and (1/)(/)(/)xxbcrbxcr bx 
(50)
On the other hand, the immune system will experience
equilibrium when
23
304231 3
2
0
xx
xsc x xdx
x
  

(51)
at state
02
3124 222
()
( )( )
sx
xdxc xxx

 

 
(52)
Provided that
124 222
( )( )dxc xxx    
Finally with free therapy
44
0 at 0 xx
with zero
control input
()ut
.
It can be seen easily that the system has three different
types of equilibria: Tumor-free (no tumor cells), Dead
(no normal tissue cells), and Coexisting (both normal
and tumor cells exist) equilibrium points [4]. In the con-
text of developing therapy strategy, Tumor-free or Coex-
isting type equilibrium points should be reached, since in
these types of states, the normal cell population is close
to its healthy state. In this study, our aim is to determine
the therapy dosage to bring the system to the tumor-free
equilibrium point. The tumor-free equilibrium point of
the system is obtained as
201
(1/,0,/ ,0)bs d
which
gives us a healthy normal cell population of
2
(1/ )b
and
immune cell population of
01
( / )sd
with zero tumor
level and free drug injection. Considering now the elec-
tromagnetic equilibrium given that
56
0xx
, along
with
 
66 5
22( )0
i we we ee
i ewi e w
RCR CR C
xxxu t
R RCR RC

 
(53)
when states
65 ( )0 e
xxut 
which is not feasible
since the live cell should keep a cellular voltage in the
range of 80 - 100 millivolts. With other equilibrium state
65
2()
22
i e w
i we we eiwe we e
R R C
xxu t
RCR CR CRCR CR C
 
  
(54)
The human cell will have a steady-state heat transfer
when
77
10
h inout
hh
xxR q
RC
  
(55)
at
2
7hh inhh out
xRCqR C  
(56)
A steady-state cellular fluid flow occurs when
88
10
in
ff
xxQ
RC
 
(57)
8ff in
xR CQ
. (58)
Thus, the fluid steady-state occurs when
8ff in
xR CQ
. Fractional mass balance exist in the hu-
man cell when the oxygen flow, PH and Pancreatin sat-
isfy, respectively,
 
2
22
9 890
O
OAO in
ff
vA
xxxv AQ
RC
  
(59)
 
10 810
,0
HA in
v HH
ff
vA
xxxv AQ
RC



 
(60)
 
118 ,110
Pn v PnAPnin
ff
vA
xxxv AQ
RC
  
(61)
with oxygen equilibrium state given by
 
22
22
98
OO
in
ffO AO A
v Av
xx AQ
RC   


(62)
and PH equilibrium state defined by
 
10 8
,,
HH
in
f fAA
v HvH
v Av
xx AQ
RC   




(63)
Finally Pancreatin stability when

11 8
,,
PnPn in
ffv PnAvPnA
v Av
xx AQ
RC   


Since the normal cell-tumor-immune dynamics is
nonlinear, it is interesting to linearized the system at

M. Al-Shibli / J. Biomedical Science and Engineering 4 (2011) 569-582
577
equlibruim points for the purposed of control design.
5.2. Authors and Affiliations
It is desired at the moment to seek a linearized model of
the cells growth at the equilibrium points with zero con-
trol input in the given form
x Ax
(64)
where
A
is the Jacobian Matrix. To fulfill this goal, let
11123 4
( ,,,)xfx xxx
(65)
21123 4
( ,,,)xfx xxx
(66)
311 23 4
( ,,,)xfx xxx
(67)
41123 4
( ,,,)xfx xxx
(68)
The Jacobian matrix for the dynamics (38)-(41) can be
verified as
1111121 11 1
2 222222133243 222
322 324 22 4133
22
2
1
20
2
()
0()
0 00
rrbxc xc xa x
cxrrbxcxcxaxc xax
Axxx xxcx ax dax
x
x
d





 

  




 






(69)
Substituting now the equilibrium point
201
(1/,0,/ ,0)bs d
yields to the following linearized Jacobia Matrix
111 21 21 2
2223 01
01301
1
1
2 //0/
0//00
0/
00 0
rrb bc ba b
rcbc sd
Asda sd
d
d


 











(70)
The following tables show the generalized system pa-
rameters values used in the modeling and linearized
state-feedback control.
This linearized overall dynamical model will be the
interest of next section to investigate controllability, ob-
servability and designing a state-feedback controller
using pole placement approach. Later analysis will show
these parameters are so important in determining the
stability of the human cell, its survival and in the growth
of the tumor cells and decreasing the immune system.
Some parameters affect the normal cells growth, tumor
growth and immune system strength, cellular voltage,
heat and fluid flow, oxygen rate, acidity and pancreatin
enzyme.
 
2
2
111 21 21 2
2223 01
013 01
1
1
2 //0/0000000
0// 000000000
0/000 0000
000000 0000
000 00100000
2
2
000 000000
1
000 0000000
1
000 0000000
000 0000
i we wee
i e wi e w
hh
ff
O
O
ff
rrbbc ba b
rcbc sd
sda sd
d
d
RCR CR C
R R CR R C
ARC
RC
vA
RC



 









 
 
 
,
,
00
000 000000
000 000000
A
HA
vH
ff
Pn v PnA
ff
vA
RC
vA
RC



































(71)
The input vector is given by
2
111( )1( )
Teh inoutinOininPnin
H
BututRqQvAQ vAQ vAQ 




(72)

M. Al-Shibli / J. Biomedical Science and Engineering 4 (2011) 569-582
578
6. CONTROLABILITY AND OF TUMOR
DYNAMICS AND CONTROLLER
DESIGN
A system is said to be controllable at time
0
t
if it is
possible by means of unconstrained control vector to
transfer the system from an initial state
0
()xt
to any
other state in a finite interval time. The concepts of con-
trollability and observability were introduced by Kalman.
They play an important role in the design of control sys-
tems in state space. In fact, the conditions of controlla-
bility and observability may govern the existence of a
complete solution to the control system design. Although
most physical systems are controllable and observable,
corresponding mathematical models may not possess the
property of controllability and observability. In what
follows, we shall derive the condition for complete state
controllability. Figures 2 and 3 show the open-loop
cancer controlled systems and closed-loop cancer con-
trolled system, respectively.
Consider the continuous-time system
wxAxB
(73)
wyCx D
(74)
where,
x
is a state vector
y
is
m
-output vector
w
is a control signal
A
is
nn
matrix
B
is
1n
matrix
C
is
nm
matrix
The system described in Eq.73 is said to be state con-
trollable at
0
tt
if it is possible to construct an uncon-
strained control signal that will transfer an initial state to
any final state in a finite time interval
01
tt t
. If
every state is controllable, then the system is said to be
completely state controllable [12]. The system is said to
be controllable if and only if the following
nn
matrix
is full rank
n



2n 1
B AB ABAB
(75)
This matrix is called the controllability matrix.
A system is said to be observable at time
0
t
, if with
the system in state
0
()xt
, it is possible to determine its
state from the observation of the output over a finite time
interval.
The concept of observability is very important be-
cause , in practice, the difficulty is encountered with
state feedback control is that some of the state variables
are not accessible for direct measurement , with the re-
sult that it becomes necessary to estimate the unmeasur-
able state variables in order to construct the control
signals. The system is said to be observable if and only if
the following
n nm
matrix is of full rank
n
  
TTTTTTT




2n1
CA CACAC
(76)
Matrix (76) is commonly called observability matrix.
This following analysis presents a design method
commonly called the pole-placement technique. We as-
sume that all state variables are measureable and are
available for feedback. It is shown that if the system
considered is completely state controllable, then poles of
the closed-loop system may be placed at any desired
locations by means of state feedback through an appro-
priate state feedback gain matrix. Let us assume the de-
sired closed-poles are to be at
11
s  
,
22
s  
,…,
nn
s  
.
We shall choose the control signal to be
wKx
(77)
This means that the control signal is determined by an
instantaneous state. Such a scheme is called state feed-
back. The
1n
matrix
K
is called the state feedback
gain matrix. Substituting (77) into Eq .73 gives
 
( )()ttxABK x
(78)
The solution of this equation is give by
 
( )(0)t te

A BK xx
(79)
where is the initial state caused by external disturbances.
The stability and transient response characteristics are
determined by the egienvalues of matrix
A BK
. If
matrix
K
is chosen properly, the matrix
A BK
can
be made asymptotically stable matrix.
Define a transformation matrix
T
by
T MW
(80)
Figure 2. Open-loop cancer controlled system.
Figure 3. Closed-loop cancer controlled system.



M. Al-Shibli / J. Biomedical Science and Engineering 4 (2011) 569-582
579
where
M
is the controllability matrix



2n 1
B AB ABAB
(81)
and
12
23
1
1
10
10 0
100 0
nn
nn
a aa
aa
a










W
(82)
where the

i
as
are the coefficients of the characteristic
polynomial
1
11
nn nn
ssa sasa


 IA
(83)
Let us choose a set desired egienvalues as
11
s  
,
22
s  
,···,
nn
s  
. Then the desired characteristic
equation becomes
1
1 211
()() ()nn
nnn
ssss ss 


 
(84)
The sufficient condition that the system to be com-
pletely controllable with all egienvalues arbitrarily
placed by choosing the gain matrix
   
1
11221 1n nnn
aaa a   


  

KT
(85)
The former outlined control design will be validated
in the following section by demonstrating the simulation
results.
Simulation Results
Every cell in the human body functions as a micro bat-
tery. To successfully bring nourishment in and take poi-
sons out, it has to be fully charged. In a cancerous cell,
the cell voltage drops from 90 millivolts to less than 40
millivolts. When the cell voltage gets to the very bottom,
only 5 substances can pass in or out of the cell. They are
water, sugar, potassium, cesium and rubidium [12]. Ox-
ygen cannot enter into a cancer cell. Even if there is a lot
of oxygen in the blood, it cannot get into the cell. Ce-
sium, because of its electrical properties can still enter
the cancerous cell. When it does so, because of its ex-
treme alkalinity, the cell dies. Luckily, healthy cells are
not affected by cesium because their cell voltage allows
them to balance themselves. This uptake can be en-
hanced by Vitamins A and C as well as salts of zinc and
selenium. The quantity of cesium taken up was sufficient
to raise the cell to the 8 pH range. Where cell mitosis
ceases and the life of the cell is short.
The objective of the Cesium therapy is to kill the tu-
mor cells, minimize the amount of drug application and
to keep cellular voltage, thermo-fluid transfer and cellu-
lar ingredients at fixed rates. In the simulated general-
ized cancer model, the healthy equilibrium point with
the parameter set given in Table 1 is (1, 0, 1.65, 0, 0.1, 0,
7.4488 ×
6
10
, 1.6 ×
6
10
, 0, 0, 0) is locally stable. It
means that the growth of cancer is controllable if suffi-
cient drug surveillance is guaranteed.
In the absence of sufficient immunee control, the tu-
mor cells grow in number and kill the healthy tissue cells
and reach the limit capacity, which is referred to as dead
equilibrium point. The initial states, i.e., the conditions
when the chemotherapy treatment is started, are assumed
to be: N(0) = 1, T(0) = 0.20, I(0) = 1, M(0) = 1). The
response of treatment-free cancer growth with respect to
normalized time scale is given in Figures 4-6. Simula-
tion analysis shows the following sensitivity of parame-
ters that affect the cell stability.
The egienvalues of matrix A have some positive val-
ues, zero, and imaginary with negative real values. Thus
the original system is unstable. These egienvalues are
listed as follows:
–0.0002 + 0.1291i,
–0.0002 – 0.1291i
–1.0000,
–0.2000
–0.6500
–0.2000
–0.0000
2.0050
2.2100
2.0100
–0.0000
Since the original dynamics is unstable, it is now de-
sired to design a state-feedback controller with the fol-
lowing desired egienvalues: –0.1, –0.1, –0.2, –0.2, –0.3,
–0.3, –0.4, –0.4, –0.5, –0.1, –0.1. As it can be seen, all
desired eigenvalues are negative and close to the origin
to guarantee a stable and fast response.
Before proceeding in the controller design, the con-
trollability condition defined by Eq.75 must be satisfied.
Considering coefficient matrix A defined (71), the input
vector given by (72), and parameters values listed in
Table 1, it is found out that the controllability matrix is
of full rank 11.
Simulation results in Figures 4-6 shows that the ce-
sium therapy is so effective in brining the normal and
immune system to its equilibrium state and forcing the
tumor cell kill. As it can be seen from the earlier analayis,
having no closed-loop controlled tumor therapy, the
overall bio-thermo-fluidic-dynamical system was un-
stable. Enforcing a state-feedback pole placement
cloride-cesium tumor therapy, a complete therapy of
disease is achieved as shown in Figure 4. Normal and
immune cells have been brought to an equilibrium state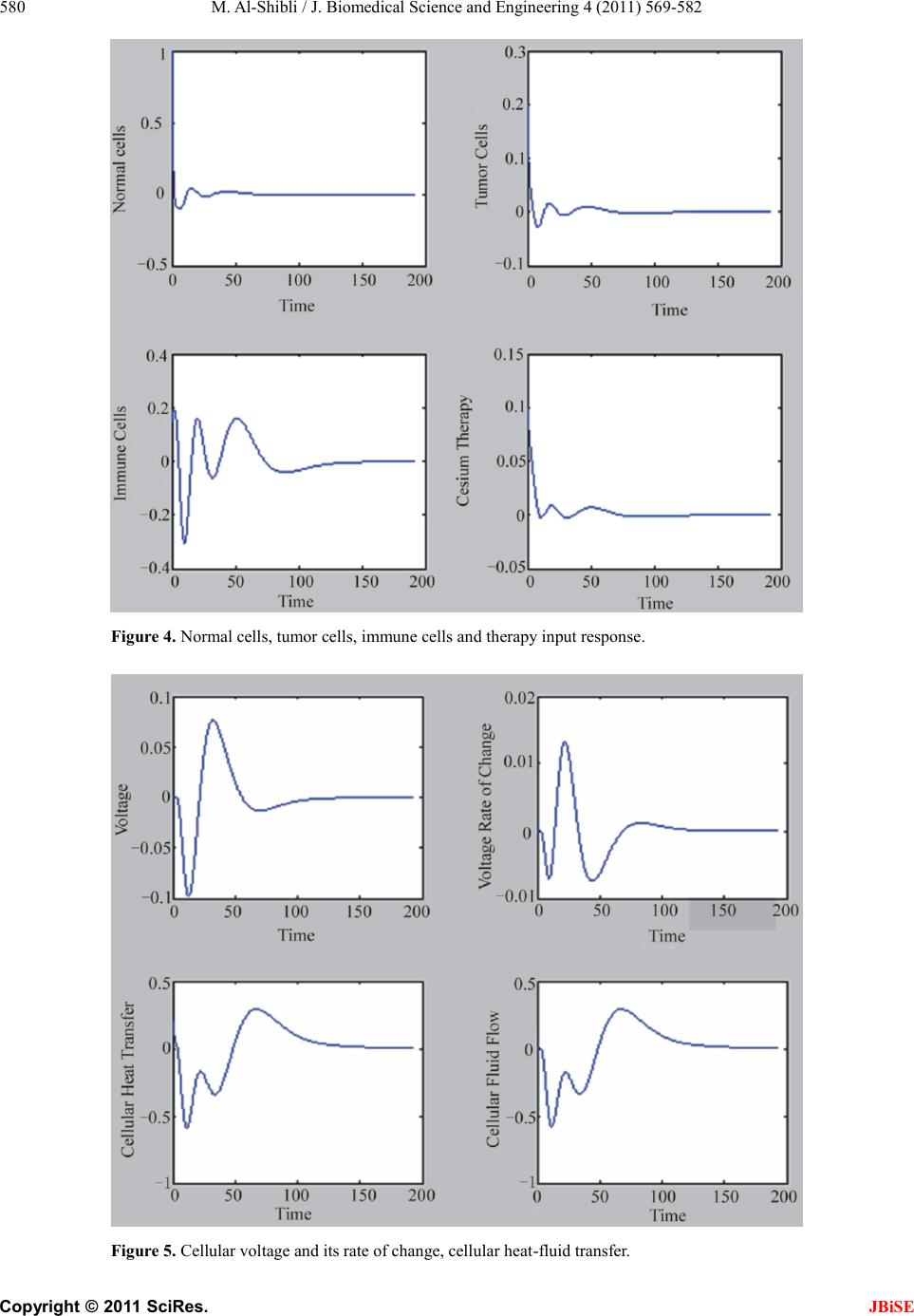

M. Al-Shibli / J. Biomedical Science and Engineering 4 (2011) 569-582
580
Figure 4. Normal cells, tumor cells, immune cells and therapy input response.
Figure 5. Cellular voltage and its rate of change, cellular heat-fluid transfer.

M. Al-Shibli / J. Biomedical Science and Engineering 4 (2011) 569-582
581
Figure 6. Fractional mass of oxygen, hydrogen ion and Pancreatin Enzyme.
by enforcing free kill cells.
Similarly, the cellular voltage is regulated at the re-
quired value. Transfer of heat and fluid from and into the
cell is maintained fixed as well. Since oxygen is so sig-
nificant to maintain a healthy cell and reduce or kill the
tumor cells its control was so efficient to keep the normal
and immune cells as desired. Acidity is controlled by the
amount of hydrogen ions in the cell as well. Finally, Pan-
creatin ratio (which has an important role in killing tumor
cells) is kept within the normal range as well.
 If
9
10
i
R
or
9
10
e
R
(Independently), the
system is unstable.
 If both
7
10
ie
RR
, the system is unstable.
 Increasing
i
R
, immunity increases.
 Decreasing
e
R
, immunity increases significantly (20
times manifold).
 Decreasing wall capacitance
W
C
increases the nor-
mal cells, tumor cells and immune cells and all oth-
ers.
 Increasing of area ratio
A

to 2.8, oscillations oc-
curs; and at 2.9 it results in unstable cells.
 Increasing oxygen ratio
2
O

to 3 will generate oscil-
lations; and to 3.8 produces unstable cells.
 Decreasing hydrogen ratio
H


to 0.01 and oxygen
rate
2
O

at 0.021 , generates unstable cells.
Increasing Pancreatin ratio
Pn

to 6 produces unsta-
ble cells.
7. CONCLUSIONS
This paper presents a more generalized dynamical model
describing the normal-tumor-immune growth consider-
ing the electro-thermo-fluidic-chemical characteristics of
a human cell. Equilibrium and stability of such a model
is validated via state-feedback controller design. Cesium
therapy is found to be so effective in controlling the
whole system. The sensitivity and the range of the dy-
namic parameters that influence the normality and im-
munity of the live cell have been identified. It is figured
out that the cellular voltage is so important to regulate
the cell normal operation. Three cellular components
have been investigated: oxygen (to keep the cell alive
and prevent cancer growth, hydrogen (acidity: PH value)
and Pancreatin enzyme (to kill the tumor cells). Simula-
tion of the controlled therapy shows how is approach is
so efficient and can be implemented clinically.

M. Al-Shibli / J. Biomedical Science and Engineering 4 (2011) 569-582
582
REFERENCES
[1] Hanahan, D. and Weinberg, R.A. (2000) The hallmarks
of cancer. Cell Journal, 100, 57-70.
doi:10.1016/S0092-8674(00)81683-9
[2] Raines, J.K. (1981) Electromagnetic field interactions
with the human body: Observed effects and theories.
Technical Report, NASA, Goddard Space Flight Center,
Washington.
[3] De Pillis, L.G. and Radunskaya, A.E. (2003.) The dy-
namics of an optimally controlled tumor model: A case
study. Mathematical and Computer Modeling, 37, 1221-
1244. doi:10.1016/S0895-7177(03)00133-X
[4] Itik M., Salamci, M.U. and Banks, S.P. (2010) SDRE
optimal control of drug administration in cancer treat-
ment. Turkish Journal of Electrical Engineering and Com-
puter Sciences, 18, 715-729.
[5] Szymanska, Z. (2003) Analysis of immunotherapy mod-
els in the context of cancer dynamics. International
Journal of Applied Mathematics and Computer Science,
13, 407-418,
[6] Byrne, H.M., Alarcon, T., Owen, R., Webb, S. D. and
Maiki, P.K. (2006) Modelling aspects of cancer dynam-
ics: A review. Philosophical Transaction of the Royal
Society A, 364, 1563-1578.
[7] Kirschner, D. (2009) On the global dynamics of a model
for tumor immunotherapy. Mathematical Biosciences
and Engineering, 6, 573-583.
[8] U. Ledzewicz, (2005) Optimal control for a system mod-
elling tumor anti-angiogenesis. ACSE 2005 Conference,
Cairo, 19-21 December 2005.
[9] Ghaffari, A. and Nasserifar, N. (2009) Mathematical
modeling and lyapunov-based drug administration in
cancer chemotherapy. Journal of Electrical & Electronic
Engineering, 5, 151-158.
[10] Warburg, O.H. (1969) The prime cause and prevention of
cancer. 2nd Edition, Konrad Triltsch, Würzburg.
[11] Brewer A.K. (1984) The high ph therapy for cancer, tests
on mice and humans. Pharmacology Biochemistry &
Behavior, 21, 1-5.
[12] Aenold J. (2003) Clean out your arteries at home, with-
out a needle, and at a fraction of the cost,” Health Sci-
ences Institute Members Alert, 1-4.