Journal of Quantum Informatio n Science, 2011, 1, 96-103
doi:10.4236/jqis.2011.12013 Published Online September 2011 (http://www.SciRP.org/journal/jqis)
Time Dependent Wave Packet Study of the H− + H2
Nonreactive Scattering
Sinan Akpinar*, Seda Surucu
Department of Physics, Faculty of Science, Firat University, Elazig, Turkey
Received July 4, 2011; revised August 10, 2011; accepted August 22, 2011
Abstract
Time dependent wave packet calculations have been performed for the H−
+ H2 nonreactive scattering,
summed of elastic and inelastic probabilities, on the recent reported potential energy surface of the 3 H

systems. The total probabilities for total angular momentum J up to 35 have been calculated to get the con-
verged integral cross sections over collision energy range of 0.20 - 1.42 eV. Integral cross-sections and rate
constants have been calculated from the wave packet transition probabilities for the initial states (υ = 0, j = 0)
by means of J-shifting method and uniform J-shifting method for J > 0.
Keywords: Reaction Dynamics, Non-Reactive Scattering
1. Introduction
The quantum wave packet method is especially useful
and transparent for studying the dynamics of elementary
chemical processes, because it allows the direct calcula-
tion of the observables and shows the possible elemen-
tary mechanisms. Over the past years, several wave
packet methods were suggested and become very popular,
and significant progress in this method has been done in
order to solve better the time dependent Schrödinger
equation (i.e., more efficient iterative method, the use of
better representations) [1-9].
The ion-molecule reactions are of interest in under-
standing the collision processes in interstellar media, the
plasma, and high-energy physic studies [10-24]. How-
ever, there have been a number of experimental and
theoretical studies on the reaction cross sections of H− +
H2 reactions and its isotopic variants [10-16]. Experi-
mentally, Michels and Paulson [15] measured the reac-
tion cross sections for the collisions of H− and D− with
H2, D2, and HD using the tandem mass spectrometer
(TMS). Muller et al. [17] performed crossed beam
measurement of rotationally inelastic scattering of H2
from H−. Haufler et al. [18] determined the integral cross
sections for the H− + D2 and D− + H2 reactions and a
pronounced isotope effect was found in the experiment.
Theoretically, an analytical ab initio Potential Energy
Surface (PES) for the ground electronic state of 3
H

was reported by Starck and Meyer (SM) [19]. Gianturco
and Kumar [20] calculated the differential and integral
cross sections for vibrationally in elastic processes in
(H-,H2) collisions over collision energy (107.69-922.4
kcal/mol) on SM PES. Recently, Panda and Sathya-
murthy [21] have computed an ab initio PES of 3
H

systems using coupled cluster singles and doubles with
nonperturbative triples method for a wide range of ge-
ometries. Subsequently, there are many theoretical stud-
ies about the title reactions using this global ab initio
potential energy surface (PES) [10,21,22]. The pioneer
work by Michels and Paulson [15] reported the biggest
theoretical value of the cross section of this system (i.e,
2.5 Angs squared). Panda and Sathyamurthy [21] used
the time dependent quantum mechanics method within
the centrifugal sudden approximation for computing the
integral reaction cross section values for H− + H2 reac-
tion (υ = 0, j = 0) and its isotopic variants. Their results
were also found to be in good agreement with the ex-
perimental results of Muller et al. [17] but larger than
those of Haufler et al. [18]. Using SM PES, Morari and
Jaquet [14] calculated the excitation function for the ex-
change reaction by including coriolis coupling and they
found the results were in agreement with experimental
results of Muller et al. [17] for all the range of energies
studied and not with those of Haufler et al. [18]. Re-
cently, using ab initio PES of Ref. 21 and time-depend-
ent wave-packet quantum method, Yao et al. [10] calcu-
lated the cross sections for both the reaction D− + H2 and
the reaction H− + D2 in the collision energy range of 0.2 -

97 S. AKPINAR ET AL.
2.4 eV. Their calculations showed that the Coriolis cou-
pled method was more consistent with the experimental
ones than the centrifugal sudden approximation, and a
pronounced isotopic effect was also observed to compare
the two reactive systems in their previous report [10].
Giri et all. have computed the differential and integral
cross sections for elastic and two dimensional inelastic
H− + H2 (υ = 0, j = 0,1) reactions at four different relative
translational energies (Etrans = 1.66, 2.03, 2.40 and 2.79
eV) by a time independent quantum mechanical ap-
proach [23]. To our knowledge, there are no experiment-
tal rate constant results of H− + H2 nonreactive scattering
to compare in all the energy ranges studied in this paper.
So, up to now, theoretically, there are not any three-di-
mensional studies of H− + H2 nonreactive scattering us-
ing time dependent quantum wave packet method to ob-
tain cross sections and the reaction rates.
Here, we report three dimensional time dependent
quantum calculations of
H
 + H2(υ, j) 
H
 + H2(υ', j')
nonreactive scattering with υ and j being the vibrational
and rotational quantum numbers. We use the 3
H

po-
tential energy surface of Panda and Sathyamurthy for all
the calculations. For computational reasons, we restrict
our calculations for total angular momentum J = 0 and
use the J-shifting approximation [25] and uniform J-
shifting approximation [26] to evaluate cross sections
and rate constants.
The paper is organized as follows. In Section 2 we
give a brief description of methodology. The results of
our calculations are presented in Section 3.
2. Theory
In this work, we employed Jacobi coordinates (R, r, γ),
which are ideally suited for the calculation of the nonre-
active state-to state and total probabilities. The corre-
sponding Hamiltonian operator for J = 0 is expressed as

22
2
2222
11 11
ˆˆ
22 22
,,
Rr Rr
j
RrRr
VRr
 



 







(1)
where r and R, respectively, the diatomic (H-H) and
atom-diatom (H–-H2) distances with
R

and r

as
their reduced masses. γ is the angle between R and r.
denotes the diatomic rotational angular momentum,
ˆ
j

,,VRr


is the potential energy function for atom-
molecule reaction.
Using the Hamiltonian operator in the form given in
Equation (1) makes it necessary to use a large number of
grid points in both R and r and an imaginary damping
potential in the end of each grid. Having added and sub-
tracted to the Hamiltonian opera-
tor given by Equation (1), we get

,, 180VR r   
 
22 22
22
ˆˆ
ˆ,,
22BC
RR
jURrH r
RR







(2)
where HBC(r) is the Hamiltonian operator for the dia-
tomic molecule and U(R,r,γ) = V(R,r,γ) – V(R = ,r, γ =
180).
Starting from the initial wave packet at t = 0 which is
constructed according to the initial system, the time-de-
pendent Schrödinger equation is solved in terms of
modified complex Chebichev polynomials [2],



min
2
0
0
,,,2 2
EN
iVt
nn
n
Et
Rr teJ  
 





n



 







(3)
where



ˆ,,,0
n nnorm
CiH Rrt 


  with ψ(R, r, γ,
t = 0) is the initial wavefunction, Cn(x) are complex Che-
bichev polynomials (CP), Jn(x) is the Bessel functions
and ΔE is the magnitude of the entire energy spread of
the spectrum of the unnormalized Hamiltonian operator
ˆ
H
. The propagation requires the operation of the


ˆ
H
nnorm
on ψ. This is performed by using a three-
term recursion relation of the Chebichev polynomials
Ci
1
ˆ
2
nnorm nn
iH 1



  (4)
where the recurrence is started by setting two initial values
as


0,,,0Rr t


 and


1ˆ,,, 0. norm
iHR rt  
The initial wavepacket is located in the asymptotic re-
gion of entrance channel and propagated on the potential
energy surface toward the strong interaction region. We
wish to compute state-to-state nonreactive scattering
probabilities and we have to follow the development of
the wavepacket being reflected from the interaction re-
gion. The flux that goes into reactive channel is absorbed
and not analyzed. In order to extract the cross section and
other observable quantities from the wavepacket dynam-
ics, the wavepacket is analyzed at each time step by tak-
ing cuts through at a fixed value of the scattering coor-
dinate R = R∞.



0
,, ,
vjkjkkvj
k
r
CtRr tPwrdr  

  





 (5)
where


,, ,
k
Rr t 
 is initial wave function,


j
k
P


is an angular wave function for a rotational state j,


vj is vibrational wave function of H2 molecule, wk
are the weights in Gauss quadrature formula. The transi-
tion probabilities for the production of specific final vi-
brational–rotational states from a specified initial reac-
tant level are given by [26-28].
r 

 

2
2
'
0
,' '
vj
J
vj vjvjvj
Rr v
A
E
PE kk
fk




 (6)


S. AKPINAR ET AL.
98
where Av′j′(E) is the Fourier transform of time-dependent
coefficients (Cν′j′(t)). vj and are the wave vectors
for initial and final channels.
k'vj k

v

f
k is the Fourier
transform of initial Gaussian.
When using a time-dependent quantum method for
scattering problems one is always faced with numerical
difficulties associated with the reflection of the wave
function from the end of the grid. Therefore, in order to
avoid such a reflection, an imaginary potential is used to
damp the wave packet at the edges of the grid. The ab-
sorbing potential parameters are optimized as instructed
by Vibok and Balint-Kurti [29]. At present calculations,
a negative complex damping potential with a quadratic
form has been used at both edges of the grid.
Usually, it is not possible to obtain the integral cross
sections and the thermal rate constants by nonreactive
probabilities calculated for J = 0. Because, all important
J values must be used to calculate the cross sections, and
for high J values each calculation becomes very difficult.
This problem is often handled approximately by the
J-shifting method [25]. In general, J-shifting method,
which is relies on the identification of “bottleneck” ge-
ometry, such as a transition state, works very well when
the reaction proceeds through an energy barrier, as is the
case for present system. The changes in rotational energy
of the system, when fixed at this geometry, provide an
energy shift ,
J
K
s
hift
E, which is used in estimating the non-
reactive probabilities and depends on the J and K quan-
tum numbers. When K = 0, there is no component on an-
gular momentum and the relationship is

0
,,
JJ J
vj vjvj vjshift
PPEE

 


(7)
where is the accurately computed nonreac-
tive probability for J = 0, at the total energy E, and
,
 is the estimated nonreactive probability for
another value of J.

0
,
J
vj vj
PE



E
J
vj vj
P
The calculation of total cross sections requires having
the transition probabilities for all available J values:
 
2
0
π21
J
vj Colvj
J
vj
EJ
k








PE (8)
where Ecol = E – εvj is the collision energy and εvj is the
initial rovibrational energy of the diatomic molecule,
is the energy-dependent total reaction probabil-
ity for a given initial state

J
vj
PE
The state-to-state rate constant can be calculated by
Boltzmann averaging of the integral cross section over
collision energy


12
/
33
0
8de
Col B
EkT
vjCol ColvjCol
RB
kTEEE
kT








(9)
where kB is the Boltzmann constant, T is temperature [30].
Another very appealing method for evaluating nonre-
active rate constants is the Uniform J-Shifting approach
developed by Zhang and Zhang [26]. In this approach,
the optimized value of rotational constant (B) at a given
temperature (T) for a range (Ji and Ji + 1) of J value is ex-
tracted from these accurate probability functions,



1
11
ln1, 2
11
i
i
J
B
iJ
ii ii
kT Q
BT i
JJ JJQ




 
(10)
where i
J
Q and 1i
J
Q

are partition like functions for Ji
and Ji + 1 reference angular momentum and can be written
in a simple form




/
ed
iicolB
JJEkT
col Col
QT PEE

 (11)
and




11/
ed
iicolB
JJEkT
col col
QT PEE


 (12)
In result, the rate constant is given by
  
 
1/2
1
0
33 3
2π21e
iB
B
TJJkT
J
B
kTQ TJ
kT 




 
(13)
3. Results and Discussions
We have calculated the rovibrational nonreactive prob-
abilities at J = 0 for 0,0, 1,2j


 propagating of
initial wave packet in Jacobi coordinates R, r, and

,
using the parameters of Table 1. The calculation re-
quired 40000 iterations steps to converge. The potential
energy surface of Ref. [21] has been used in this paper. It
has in the following features: 1) Barrier height (0.47 eV)
of proposed potential energy surface found to be a mini-
mum for the collinear geometry, with the saddle point
located at 1.999a0. 2) A van der Waals minimum was
also found for the collinear geometry at r = 1.419a0 and
R = 5.915a0 (a0 is Bohr radius) with a well of depth
0.0475 eV. 3) This potential has been constructed by fit-
ting an analytical function to the ab initio potential en-
ergy values computed using coupled cluster singles and
doubles.
Figure 1 shows nonreactive transition probabilities in
0, 0j


 at total angular momentum J = 0, 15, 25,
35 obtained from Equation (7) as a function of the colli-
sion energy. Transition probabilities show no threshold
and decrease with increasing collision energy as ex-
pected for a nonreactive scattering with a small barrier to
the reactive channel. That is, after barrier height for J = 0,
the nonreactive probability decreases slowly in the en-
ergy interval considered. Therefore, it can be seen non-
reactive probabilities rapidly shift towards higher ener-
gies on increasing J values. Probabilities are very small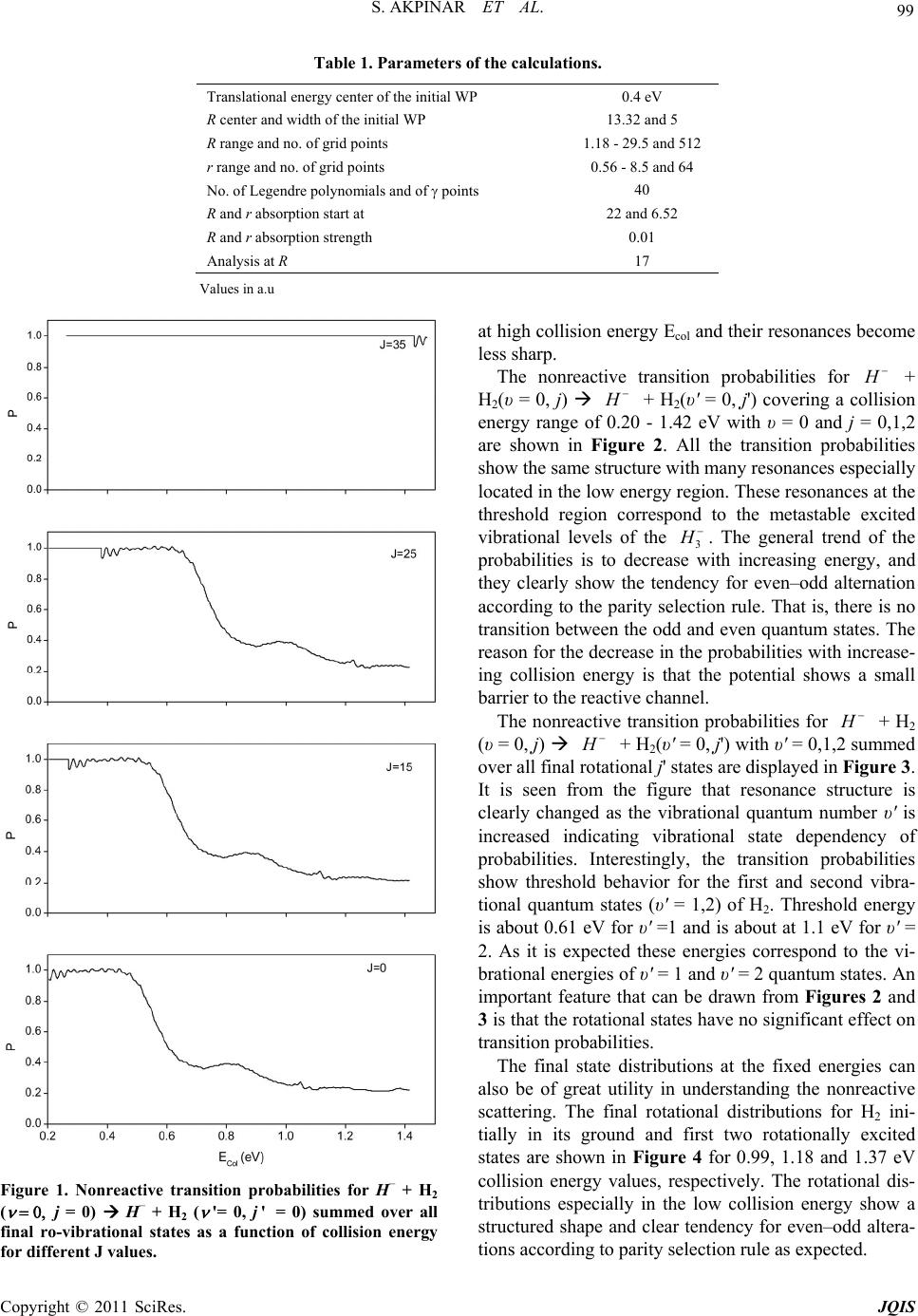

S. AKPINAR ET AL.
99
Table 1. Parameters of the calculations.
Translational energy center of the initial WP 0.4 eV
R center and width of the initial WP 13.32 and 5
R range and no. of grid points 1.18 - 29.5 and 512
r range and no. of grid points 0.56 - 8.5 and 64
No. of Legendre polynomials and of  points 40
R and r absorption start at 22 and 6.52
R and r absorption strength 0.01
Analysis at R 17
Values in a.u
at high collision energy Ecol and their resonances become
less sharp.
The nonreactive transition probabilities for
H

+
H2(υ = 0, j) 
H

+ H2(υ' = 0, j') covering a collision
energy range of 0.20 - 1.42 eV with υ = 0 and j = 0,1,2
are shown in Figure 2. All the transition probabilities
show the same structure with many resonances especially
located in the low energy region. These resonances at the
threshold region correspond to the metastable excited
vibrational levels of the 3
H
. The general trend of the
probabilities is to decrease with increasing energy, and
they clearly show the tendency for even–odd alternation
according to the parity selection rule. That is, there is no
transition between the odd and even quantum states. The
reason for the decrease in the probabilities with increase-
ing collision energy is that the potential shows a small
barrier to the reactive channel.
The nonreactive transition probabilities for
H

+ H2
(υ = 0, j) 
H

+ H2(υ' = 0, j') with υ' = 0,1,2 summed
over all final rotational j' states are displayed in Figure 3.
It is seen from the figure that resonance structure is
clearly changed as the vibrational quantum number υ' is
increased indicating vibrational state dependency of
probabilities. Interestingly, the transition probabilities
show threshold behavior for the first and second vibra-
tional quantum states (υ' = 1,2) of H2. Threshold energy
is about 0.61 eV for υ' =1 and is about at 1.1 eV for υ' =
2. As it is expected these energies correspond to the vi-
brational energies of υ' = 1 and υ' = 2 quantum states. An
important feature that can be drawn from Figures 2 and
3 is that the rotational states have no significant effect on
transition probabilities.
The final state distributions at the fixed energies can
also be of great utility in understanding the nonreactive
scattering. The final rotational distributions for H2 ini-
tially in its ground and first two rotationally excited
states are shown in Figure 4 for 0.99, 1.18 and 1.37 eV
collision energy values, respectively. The rotational dis-
tributions especially in the low collision energy show a
structured shape and clear tendency for even–odd altera-
tions according to parity selection rule as expected.
Figure 1. Nonreactive transition probabilities for H– + H2
(  j = 0)  H– + H2 (  '= 0, j' = 0) summed over all
final ro-vibrational states as a function of collision energy
for different J values.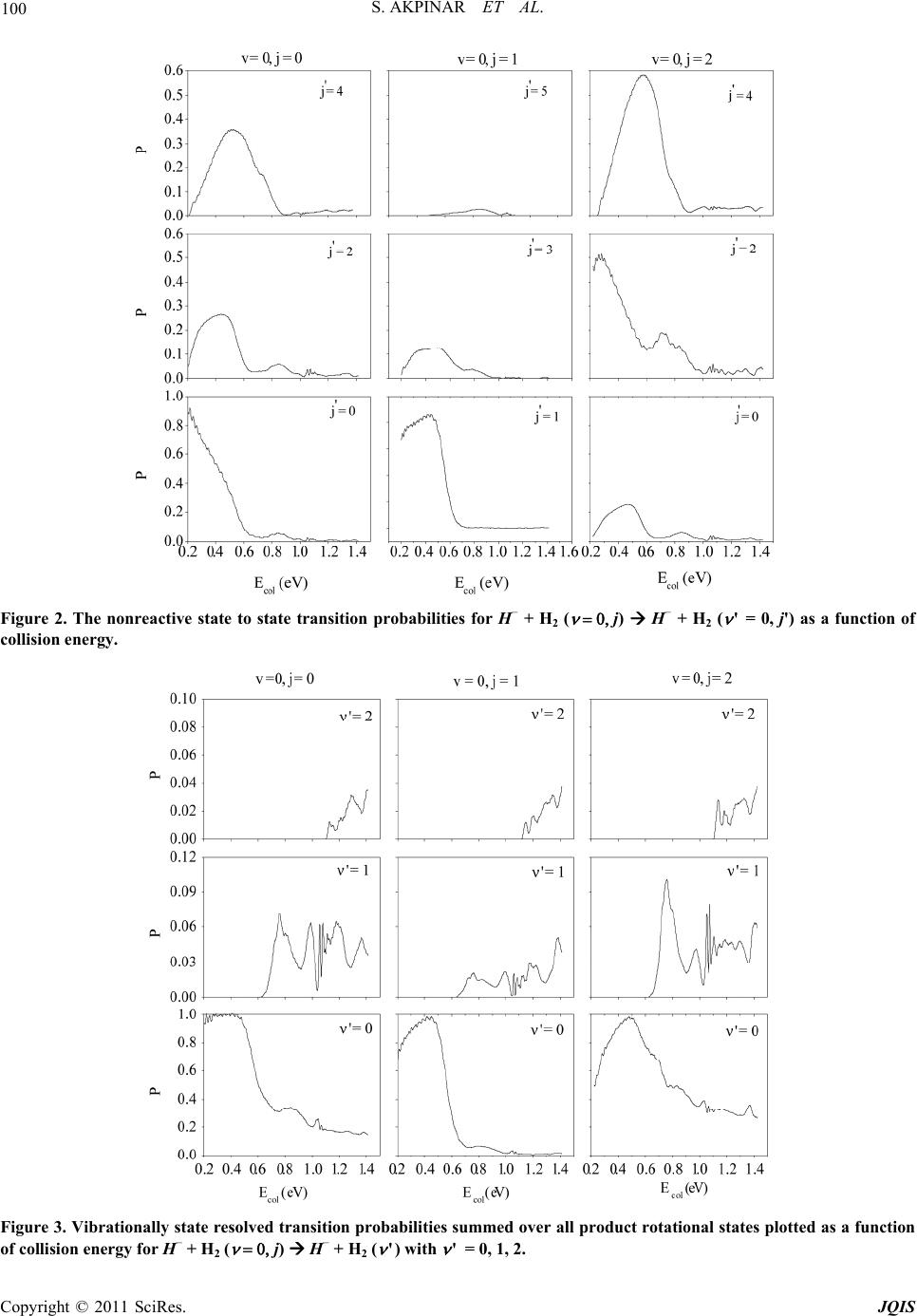

S. AKPINAR ET AL.
100
Figure 2. The nonreactive state to state transition probabilities for H– + H2 (  j)  H– + H2 (  ' = 0, j') as a function of
collision energy.
Figure 3. Vibrationally state resolved transition probabilities summed over all product rotational states plotted as a function
of collision energy for H– + H2 (  j)  H– + H2 (  ') with  ' = 0, 1, 2.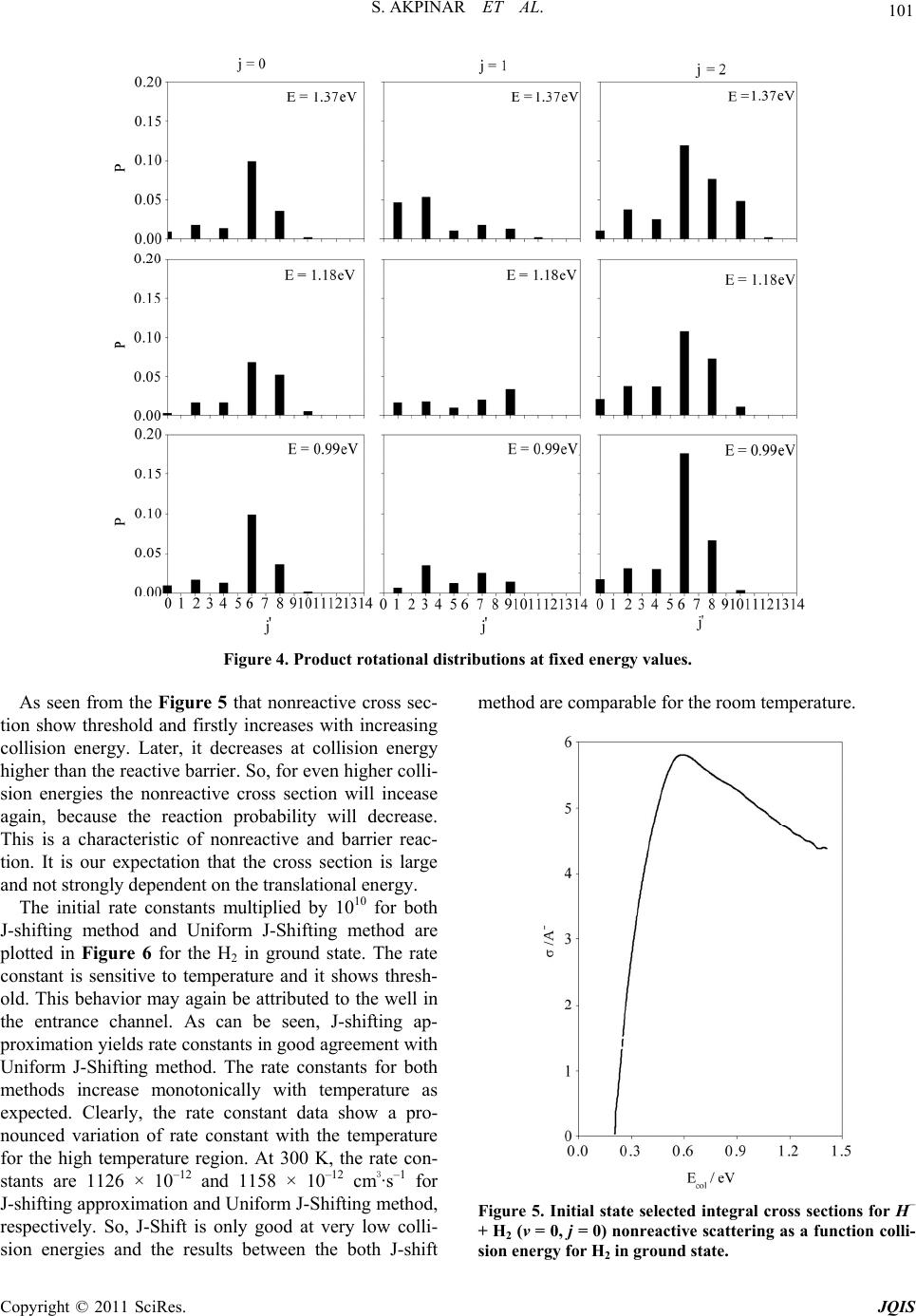

101 S. AKPINAR ET AL.
Figure 4. Product rotational distributions at fixed energy values.
As seen from the Figure 5 that nonreactive cross sec-
tion show threshold and firstly increases with increasing
collision energy. Later, it decreases at collision energy
higher than the reactive barrier. So, for even higher colli-
sion energies the nonreactive cross section will incease
again, because the reaction probability will decrease.
This is a characteristic of nonreactive and barrier reac-
tion. It is our expectation that the cross section is large
and not strongly dependent on the translational energy.
The initial rate constants multiplied by 1010 for both
J-shifting method and Uniform J-Shifting method are
plotted in Figure 6 for the H2 in ground state. The rate
constant is sensitive to temperature and it shows thresh-
old. This behavior may again be attributed to the well in
the entrance channel. As can be seen, J-shifting ap-
proximation yields rate constants in good agreement with
Uniform J-Shifting method. The rate constants for both
methods increase monotonically with temperature as
expected. Clearly, the rate constant data show a pro-
nounced variation of rate constant with the temperature
for the high temperature region. At 300 K, the rate con-
stants are 1126 × 10–12 and 1158 × 10–12 cm3·s–1 for
J-shifting approximation and Uniform J-Shifting method,
respectively. So, J-Shift is only good at very low colli-
sion energies and the results between the both J-shift
method are comparable for the room temperature.
Figure 5. Initial state selected integral cross sections for H–
+ H2 (v = 0, j = 0) nonreactive scattering as a function colli-
sion energy for H2 in ground state.

S. AKPINAR ET AL.
102
01000 2000 3000
0
1
2
3
Uniform method
J-Shifting method
k x 1010 / cm 3 s-1
T / K
Figure 6. Nonreactive rate constants depend on the initial
quantum numbers for H– + H2(v = 0, j = 0) nonreactive
scattering as a function of temperature.
4. Conclusions
In this paper, we presented a time-dependent quantum
wave packet calculation for the
H
 + H2 nonreactive
scattering and gave the dynamics information of nonre-
active probability, cross section and rate constant. The
H
 + H2 nonreactive system has an energy barrier
height on potential energy surface. The nonreactive cross
section has been obtained by summing up the nonreac-
tive probabilities. The probability for J = 0 was calcu-
lated while the probabilities for J > 0 was estimated by
means of two different J-shifting approximation. The
calculations showed that the reaction cross section shows
a threshold behavior and the initial state selected rate
constant is significantly dependent on the temperature.
5. Acknowledgements
We would like to thank Prof. N. Sathyamurthy for his
providing of potential energy function. Authors are in-
debted to Dr. Paolo Defazio for many stimulating dis-
cussions on quantum wave packet theory. Partial finan-
cial support from the Firat University Scientific Research
Projects Unit (FUBAP) (Project No: FUBAP-1775) is
gratefully acknowledged. Therefore, the numerical cal-
culations reported in this paper were performed at
TUBITAK ULAKBIM, High Performance and Grid
Computing Center (TR-Grid e-Infrastructure) and this
work was supported by the Turkish Scientific and Tech-
nological Research Council of TURKEY (TUBITAK)
(Project No. 109T447). Authors wish to thank TUBI-
TAK and FUBAP.
6. References
[1] S. C. Althorpe, “Quantum Scattering Studies of Reac-
tions,” In: P. V. R. Schleyer, Ed., The Encyclopedia of
Computational Chemistry, Wiley, Athens, 2005.
[2] H. Tal-Ezer and R. Kosloff, “An Accurate and Efficient
Scheme for Propagating the Time Dependent Schrödinger
Equation,” Journal of Chemical Physics, Vol. 81, No. 9,
1984, pp. 3967-3971. doi:10.1063/1.448136
[3] T. J. Park and J. C. Light, “Unitary Quantum Time Evo-
lution by Iterative Lanczos Reduction,” Journal of
Chemical Physics, Vol. 85, No. 10, 1986, p. 5870
doi:10.1063/1.451548
[4] J. Broeckhove and L. Lathouwers (Eds.), “Time-Depen-
dent Quantum Molecular Dynamics,” New York, Plenum,
1992.
[5] R. E. Wyatt and J. Z. H. Zhang (Eds.), “Dynamics of
Molecules and Chemical Reactions,” Dekker, New York,
1996.
[6] N. Balakrishnan, C. Kalyanaraman and N. Sathyamurthy,
“Time-Dependent Quantum Mechanical Approach to
Reactive Scattering and Related Processes,” Physical
Report, Vol. 280, No. 2, 1997, pp. 79-144.
doi:10.1016/S0370-1573(96)00025-7
[7] S. C. Althorpe and D. C. Clary, “Quantum Scattering
Calculations on Chemical Reactions,” Annual Review of
Physical Chemistry, Vol. 54, 2003, pp. 493-529.
doi:10.1146/annurev.physchem.54.011002.103750
[8] S. K. Gray and G. G. Balint-Kurti, “Quantum Dynamics
with Real Wave Packets, including Application to Three-
Dimensional (J = 0) D+H2→HD+H Reactive Scattering,”
Journal of Chemical Physics, Vol. 108, No. 3, 1998, p.
950 doi:10.1063/1.475495
[9] P. Defazio and C. Petrongolo, “Dynamics of the
N(2D)+H2 Reaction on the 2
X
A
Surface, Propagating
Real Wave Packets with an Arccos Mapping of the
Hamiltonian,” Journal of Theoretical and Computational
Chemistry, Vol. 2, No. 4, 2003, p. 547.
doi:10.1142/S0219633603000732
[10] L. Yao, L. P. Ju, T. S. Chu and K. L. Han, “Time-De-
pendent Wave-Packet Quantum Scattering Study of the
Reactions D−+H2→H−+HD and H−+D2→D−+HD,”
Physical Review A, Vol. 74, No. 6, 2006, p. 062715.
doi:10.1103/PhysRevA.74.062715
[11] S. Mahapatra, N. Sathyamurthy, S. Kumar and F. A. Gi-
anturco, “Transition State Resonances in Collinear (H−,
H2) Collisions,” Chemical Physics Letters, Vol. 241, No.
3, 1995, p. 223. doi:10.1016/0009-2614(95)00633-F
[12] A.N. Panda, K. Giri and N. J. Sathyamurthy, “Three Di-
mensional Quantum Dynamics of (H−, H2) and Its Iso-
topic Variants,” The Journal of Physical Chemistry A,
Vol. 109, No. 10, 2005, pp. 2057-2061.
doi:10.1021/jp044953l
[13] A.N. Panda and N. Sathyamurthy, “Time-Dependent
Quantum Mechanical Wave Packet Study of the
He+H2+(v,j)→HeH++H reaction,” Journal of Chemical
Physics, Vol. 122, No. 5, 2005, p. 054304.
doi:10.1063/1.1839866
[14] C. Morari and R. Jaquet, “Time-Dependent Reactive
Scattering for the System H−+D2↔HD+D− and Com-

103 S. AKPINAR ET AL.
parison with H-+ H2↔ H2+ H,” The Journal of Physical
Chemistry A, Vol. 109, 2005, p. 3396.
doi:10.1021/jp0462963
[15] H. H. Michels and J. F. Paulson, In: D. G. Truhlar, Ed.,
Potential Energy Surface and Dynamics Calculations,
Plenum Press, New York, 1981.
[16] M. S. Huq, L. D. Doverspike and R. L. Champion, “Elec-
tron Detachment for Collisions of H− and D− with Hy-
drogen Molecules,” Physical Review A, Vol. 27, No. 6,
1982, pp. 2831-2839. doi:10.1103/PhysRevA.27.2831
[17] H Müller, M Zimmer and F Linder, “State-Resolved
Measurements of Rotational Excitation in H−+H2 Colli-
sions at Low Energies,” Journal of Physics B-Atomic
Molecular and Optical Physics, Vol. 29, No. 18, 1996, p.
4165.
[18] E. Haufler, S. Schlemmer and D. Gerlich, “Absolute In-
tegral and Differential Cross Sections for the Reactive
Scattering of H−+D2 and D−+H2,” The Journal of Physi-
cal Chemistry A, Vol. 101, No. 36, 1997, pp. 6441-6447.
doi:10.1021/jp9707246
[19] J. Starck and W. Meyer, “Ab-Initio Potential-Energy
Surface for the Collisional System H−+H2 and Properties
of Its Van-Der-Waals Complex,” Journal of Chemical
Physics, Vol. 83, 1993, p. 176.
[20] F.A. Gianturco and S. Kumar, “Selective Efficiency of
Vibrational Excitations in Ion–Molecule Collisions: A
Comparison of Behavior for H+–H2 and H−–H2,” Journal
of Chemical Physics, Vol. 103, No. 8, 1995, p. 2940.
doi:10.1063/1.470481
[21] A.N. Panda and N. Sathyamurthy, “Dynamics of (H−, H2)
Collisions: A Time-Dependent Quantum Mechanical In-
vestigation on a New Ab Initio Potential Energy Sur-
face,” Journal of Chemical Physics, Vol. 121, No. 19,
2004, p. 9343. doi:10.1063/1.1797711
[22] T. S. Chu, R. F. Lu, K. L. Han, X. N. Tang, H. F. Xu and
C. Y. Ng, “A Time-Dependent Wave-Packet Quantum
Scattering Study of the Reaction H2
+(v = 0–2,4,6; j =
1)+He→HeH++H,” Journal of Chemical Physics, Vol.
122, No. 24, 2005, p. 4322. doi:10.1063/1.1948380
[23] K. Giri and N. Sathyamurthy, “Rotational Excitation in
(H−, H2) Collisions: A Quantum Mechanical Study,”
Journal of Physics B: Atomic, Molecular and Optical
Physics, Vol. 39, No. 20, 2006, p.4123.
doi:10.1088/0953-4075/39/20/010
[24] W. Li, M. Wang, C. Yang, X. Ma, D. Wang and W. Liu,
“Quasi-Classical Trajectory Study of the Cross Sections
of the Reactions of D−+H2→H−+HD and H−+D2→
D−+HD,” Chemical Physics Letters, Vol. 445, No. 4-6,
September 2007, pp. 125-128.
doi:10.1016/j.cplett.2007.08.013
[25] J. M. Bowman, “Reduced Dimensionality Theory of
Quantum Reactive Scattering,” The Journal of Physical
Chemistry, Vol. 95, No. 13, 1991, pp. 4960-4968
doi:10.1021/j100166a014
[26] D. H. Zhang and J. Z. H. Zhang, “Uniform J-Shifting
Approach for Calculating Reaction Rate Constant,”
Journal of Chemical Physics, Vol. 110, No. 16, 1999, p.
7622. doi:10.1063/1.478802
[27] F. Gögtas, G. G. Balint-Kurti and A. R. Offer, “Quantum
Mechanical Three-Dimensional Wavepacket Study of the
Li+HF->LiF+H Reaction,” Journal of Chemical Physics,
Vol. 104, 1996, p. 7927.
[28] G. G. Balint-Kurti, R. N. Dixon and C. C. Marston,
“Time-Dependent Quantum Dynamics of Molecular
Photofragmentation Processes,” Journal of the Chemical
Society-Faraday Transactions, Vol. 86, 1990, p. 1741.
[29] A. Vibok and G. G. Balint-Kurti, “Parametrization of
Complex Absorbing Potentials for Time-Dependent
Quantum Dynamics,” The Journal of Physical Chemistry,
Vol. 96, No. 22, 1992, pp. 8712-8719
doi:10.1021/j100201a012
[30] S. Y. Lin and H. Guo, “Quantum Wave Packet Studies of
the C(1D)+H2→CH+H Reaction?” Integral Cross Section
and Rate Constant, Vol. 108, No. 12, 2004, pp. 2141-
2148. doi:10.1021/jp031184h