Journal of Quantum Informatio n Science, 2011, 1, 73-86
doi:10.4236/jqis.2011.12011 Published Online September 2011 (http://www.SciRP.org/journal/jqis)
Bound States of the Klein-Gordon for Exponential-Type
Potentials in D-Dimensions
Sameer M. Ikhdair
Physics Department, Near East University, Nicosia, North Cyprus, Turkey
Received May 27, 2011; revised June 9, 2011; accepted June 22, 2011
Abstract
The approximate analytic bound state solutions of the Klein-Gordon equation with equal scalar and vector
exponential-type potentials including the centrifugal potential term are obtained for any arbitrary orbital
quantum number l and dimensional space D. The relativistic/non-relativistic energy spectrum formula and
the corresponding un-normalized radial wave functions, expressed in terms of the Jacobi polynomials



,,
n
Pz

1, 1

  and or the generalized hypergeometric functions

1, 1z 



21 ,;;
F
abcz
have been obtained. A short-cut of the Nikiforov-Uvarov (NU) method is used in the solution. A unified
treatment of the Eckart, Rosen-Morse, Hulthén and Woods-Saxon potential models can be easily derived
from our general solution. The present calculations are found to be identical with those ones appearing in the
literature. Further, based on the PT-symmetry, the bound state solutions of the trigonometric Rosen-Morse
potential can be easily obtained.
Keywords: Approximation Scheme, Eckart-Type Potentials, Rosen-Morse-Type Potentials, Trigonometric
Rosen-Morse Potential, Hulthén Potential and Woods-Saxon Potential, Klein-Gordon Equation,
NU Method
1. Introduction
The exact solutions of the wave equations (non-relativ-
istic or relativistic) are very important since they contain
all the necessary information regarding the quantum sys-
tem under consideration. However, analytical solutions are
possible only in a few simple cases such as the hydrogen
atom and the harmonic oscillator [1,2]. Most quantum sys-
tems could be solved only by using approximation sche-
mes like rotating Morse potential via Pekeris approxima-
tion [3-5] and the generalized Morse potential by means of
an improved approximation scheme [6]. Recently, the
study of exponential-type potentials has attracted much
attention from many authors (for example, cf, [7-39]).
These physical potentials include the Woods- Saxon [7,8],
Hulthén [9-22], modified hyperbolic-type [23], Manning-
Rosen [24-31], the Eckart [32-37], the Pöschl-Teller [38]
and the Rosen-Morse [39,40] potentials.
The spherically symmetric Eckart-type potential model
[41] is a molecular potential model which has been widely
applied in physics [42] and chemical physics [43,44] and
is generally expressed as


2
12
,cos coth
qq
Vr qVechrVr  

,
12
, 0, 10 or 0VVq q  (1)
where the coupling parameters 1 and 2 V describe the
depth of the potential well, while the screening parameter
V

is related to the range of the potential. It is a special
case of the five-parameter exponential-type potential
model [45,46]. The range of parameter was taken as
in [47] and has been extended to or
or even complex in [46]. The deformed hyper-
bolic functions given in (1) have been introduced for the
first time by Arai [48] for real values. When is
complex, the functions in (1) are called the generalized
deformed hyperbolic functions. The Eckart-type poten-
tials (1) can also be written in the exponential form as
q
0
0
q
q
10q 
qq


22
12
2
2
e1
,4 1e
1e
rr
r
r
q
VrqVV q
q2
e










 (2)
The study of both bound and scattering states for the
Eckart-type potential has raised a great deal of interest in
the non-relativistic as well as in relativistic quantum

S. M. IKHDAIR
74

mechanics. The s-wave bound-state solution of
the Schrödinger equation for the Eckart potential has
been widely investigated by using various methods, such
as the supersymmetric (SUSY) shape invariance tech-
nology [49], point canonical transformation (PCT) me-
thod [50] and SUSY Wentzel-Kramers-Brillouin (WKB)
approximation approach [51]. The bound state solutions
of the s-wave Klein-Gordon (KG) equation with equally
mixed Rosen-Morse-type (Eckart and Rosen--Morse well)
potentials have been studied [52]. The bound state solu-
tions of the s-wave Dirac equation with equal vector and
scalar Eckart-type potentials in terms of the basic con-
cepts of the shape-invariance approach in the SUSYQM
have also been studied [34-37]. The spin symmetry and
pseudospin symmetry in the relativistic Eckart potential
have been investigated by solving the Dirac equation for
mixed potentials [38]. Unfortunately, the wave equations
for the Eckart-type potential can only be solved analyti-
cally for zero angular momentum states because of the
centrifugal potential term. Some authors [32-38] studied
the analytical approximations to the bound state solutions
of the Schrödinger equation with Eckart potential by
using the usual existing approximation scheme proposed
by Greene and Aldrich [53] for the centrifugal potential
term. This approximation has also been used to study
analytically the arbitrary l-wave scattering state solu-
tions of the Schrödinger equation for the Eckart potential
[54,55]. The same approximation scheme for the spin-
orbit coupling term has been used to study the spin
symmetry and pseudospin symmetry analytical solutions
of the Dirac equation with the Eckart potential using the
AIM [56]. Furthermore, the pseudospin symmetry ana-
lytical solutions of the Dirac equation for the Eckart po-
tential have been found by using the SUSY WKB for-
malism [57]. Recently, for the first time, the approxima-
tion scheme for the centrifugal potential term has also
been used in [58] to obtain the approximate analytical
solution of the KG equation for equal scalar and vector
Eckart potentials for arbitrary -states by means of the
functional analysis method.

0l
l
This approximation for the centrifugal potential term
[9,19,53] has also been used to solve the Schrödinger
equation [9,19], KG [10-12,20-22] and Dirac equation
[20-22] for the Hulthén potential. Recently, the KG and
Dirac equations have been solved in the presence of the
Hulthén potential, where the energy spectrum and the
scattering wave functions were obtained for spin-0 and
spin- 
12 particles, using a more general approxima-
tion scheme for the centrifugal potential [20-22]. They
found that the good approximation, however, occurs
when the screening parameter

and the dimensionless
parameter

are taken as 0.1


and 1,

 respec-
tively, which is simply the case of the usual approxima-
tion [9,19]. Also, other authors have recently proposed
an alternative approximation scheme for the centrifugal
potential to solve the Schrödinger equation for the
Hulthén potential [59]. Taking 1,

 their approxima-
tion can be reduced to the usual approximation [9,19].
Quite recently, we have also proposed a new approxima-
tion scheme for the centrifugal term [13,14].
The Nikiforov-Uvarov (NU) method [60] and other
methods have also been used to solve the D-dimensional
Schrödinger equation [61] and relativistic D-dimensional
KG equation [62], Dirac equation [6,15,39,40,63] and
spinless Salpeter equation [64].
Our aim is to employ the usual approximation scheme
[53,58] in order to solve the D-dimensional radial KG
equation for any orbital angular momentum number l for
the scalar and vector Eckart-type potentials using a gen-
eral mathematical model of the NU method. This offers a
simple, accurate and efficient scheme for the exponen-
tial-type potential models in quantum mechanics. We
consider the following relationship between the scalar
and vector potentials:


0
V  

,VrSr where 0
and
V

are arbitrary constants [51]. Under the restriction
of equally mixed potentials the KG equa-
tion turns into a Schrödinger-like equation and thus the
bound state solutions are very easily obtained through
the well-known methods developed in the non-relativis-
tic quantum mechanics. It is interesting to note that, this
restriction include the case where when both
constants vanish, the situation where the potentials are
equal

Sr V
Vr

,r

0


00; 1V


 and also the case where the poten-
tials are proportional [66] when 0 and 0V1,



which provide the equally-mixed scalar and vector po-
tential case




.rVr Further, we have obtained
an approximate analytic solution of the KG equation in
the presence of equal scalar and vector generalized de-
formed hyperbolic potential functions by means of pa-
rameteric generalization of the NU method. Furthermore,
for the equally-mixed scalar and vector potential case
S




,Sr
1,
Vr we have obtained the approximate
bound state rotational-vibrational (ro-vibrational) energy
levels and the corresponding normalized wave functions
expressed in terms of the Jacobi polynomial n
where

, 

,Px

 1

 and


1,x 1 for a spin-
zero particle in a closed form [67].
The paper is structured as follows. In Section 2, we
derive a general model of the NU method valid for any
central or non-central potential. In Section 3, the ap-
proximate analytical solutions of the D-dimensional ra-
dial KG equation with arbitrary l-states for equally-
mixed scalar and vector Eckart-type potentials and other
typical potentials are obtained by means of the NU
method. Also, the exact s-wave KG equation has also
been solved for the Rosen-Morse-type potentials and

75 S. M. IKHDAIR
other typical potentials. The relative convenience of the
Eckart-type potential (Rosen-Morse-type potential) with
the Hulthén potential (Woods-Saxon potential) has been
studied, respectively. We make some remarks on the
energy equations and the corresponding wave functions
for the Eckart and Rosen-Morse well potentials in vari-
ous dimensions and their non-relativistic limits in Section
4. Section 5 contains the conclusions and the outlook.
2. Method of Analysis
The method of analysis is briefly outlined here and the
details can be found in [60]. This method was proposed
to solve the second-order differential wave equation of
the hypergeometric-type:
 


20
nnn
zz zzz zz   
    
z

z
(3)
where and are at most second-degree
polynomials and is a first-degree polynomial. The
prime denotes the differentiation with respect to z. In
finding a particular solution to (3), one needs to decom-
pose the wave function as

z 

z 


z
n




z
 
nnn
zzy   (4)
yielding the following hypergeometric type equation
  
0
nnn
zy zzy zyz 
 
 (5)
where

πk 

 (6)
and


n
y
z satisfying the Rodrigues relation
   
d
d
n
n n
nn
A
yzz z
zz






 (7)
In the above equation, n
A
is a constant related to the
normalization and is the weight function satisfy-
ing the condition

z 
 
0zzzz z  

 

 (8)
with
  
2π, 0zz zz  

 
 (9)
Since and the derivative of
should be negative [60] which is the essential
condition for a proper choice of solution. The other part
of the wave function in (4) can be defined as

0z  

0,z  

z 








π0zz zz  
 (10)
where
  
1
π2 zz   



 
2 144
2zz zk


 

 z
(11)
The determination of the root k is the essential point in
the calculation of


π,z for which the discriminator of
the square root in the last equation is being set to zero.
The results in the polynomial which is dependent
on the transformation function Also, the parameter

πz

.zr

defined in (6) takes the following form
 
11, 0,1,2,
2
nnznnzn
 


  (12)
We may construct a general recipe of the NU method
valid for any central and non-central potential model.
This can be achieved by comparing the following hyper-
geometric equation
   


2
3312
2
11
0
nn
n
zczzzczcczz
AzBz Cz





  
 
 (13)
with its counterpart (3) to obtain [67]







2
12 3
,1,zcczzz czzAzBzC  

 


(14)
Further, substituting (14) into (11) gives
 
12
2
4563,7 ,8
πzcczcck zck zc
 


  


(15)
with parametric constants
 
2
4152365
2
745 84
11
1, 2,
22
2,
ccccccc
cccBccC
A

 

(16)
The discriminant under the square root sign must be
set to zero and the resulting equation must be solved for
k, it yields


,7388
22kccccc
  9
(17)
where


93738
cccccc
6


(18)
Inserting (17) into (15) and solving the resulting equa-
tion, we make the following choice of parameters:



459388
πzcczcccz c


 

 (19)


7388
22kc cccc
 9
(20)
Equation (9) gives
 

25938 8
122zcczccczc 

 

(21)
z
whose derivative must be negative:
*The shortcut is simple and straightforward procedure helping to avoid
the difficulty in choosing the physical polynomial and the root
k.

πz



3938
22zc ccc 
0

  (22)

S. M. IKHDAIR
76
in accordance with essential requirement of the method
[60]. Solving (6) and (12), we get the energy equation:
 


2
23357 3
93889
212
212 0
ccncnncccc
nccc cc

  
8

(23)
for the potential model under consideration.
In regards of the wave functions. We firstly obtain the
solution of the differential equation (8) for the weight
function as 
z 


11
10
3
1c
c
zz cz   (24)
and hence from (7), the first part of the wave functions
can be expressed in the form of the Jacobi polynomials as



10 11
,
3
12
cc
nn
yz Pcz (25)
where and
 
10 11
Re1, Re1cc 
10 148
11149 3
3
22 1,
2
12, 0
ccc c
ccc cc
c
 
 (26)
The second part of the wave functions (4) can be found
from the solution of the differential equation (10) as


13
12
3
1c
c
zz cz   (27)
where

1248 13495
3
1
, cc ccccc
c
 


2
(28)
Hence, the general wave functions (4) read as
 


13 10 11
12 ,
33
11
ccc
c
lnl n
uz Nzcz Pcz  (29)
where is the normalization constant
nl
N
3. Bound-State Solutions
The D-dimensional time-independent arbitrary l-state
radial KG equation with scalar and vector potentials
and respectively, where

Sr

,Vr rr describ-
ing a spineless particle takes the general form [3,62]:


 


1
12
1
12
2
,, 22
2
222
,,
1
ˆ
0,
D
D
D
D
ll
Dll
ll
nlD ll
xc
EVr McSr

















(30a)
2
2
2
1
,
D
D
j
j
x


 
 (30b)




11
12 12
12 1 ,, ,,
ˆ(), , ,
DD
DD
ll ll
lD
ll ll
xRrY 






  (30c)
where M and ,
nl
E2
D
 stand for KG energy, mass and
D-dimensional Laplacian, respectively. In addition, x is a
D-dimensional position vector. Let us decompose the
radial wave function


l
Rr

as follows:


12D
l
r

l Rr ur (31)
we, then, reduce (30a) into the D-dimensional radial
Schrödinger-like equation with arbitrary orbital angular
momentum number l as
 
 
2
nl
l
ur


222
22
22
2
d() 1
d
10
l
c
ur EVr MSr
rc
ll c
r


 


 
 










(32)
where we have set

2
1214M

 



ll

 
and
2
M
Dl


 where 0,1l,2,.

 Under the equally
mixed potentials


Sr

,Vr the KG turns into a
Schrödinger-like equation and thus the bound state solu-
tions are very easily obtained with the help of the well-
known methods developed in the non-relativistic quan-
tum mechanics. We use the existing approximation for
the centrifugal potential term in the non-relativistic
model [9,19] which is valid only for value [62,
68]:
1q





2
2
1
,
 
22
e
41 ,
1e
32
r
r
ll
Vrl l
rq
lM




 





(33)
in the limit of small

and .l
3.1. The Eckart-Type Model
At first, let us rewrite Equation (2) in a form to include
the Hulthén potential,


22
12
r
V3
22 2
2
e1e
,4 1e 1e
1e
rr
rr
q
Vrq VV
qq
q









 (34)
and then follow the model used in [62,68,69] by inserting
the above equation and the approximate potential term
(33) into (32), we obtain










 
2
222
2222 2
2
2
22
23
2
22
d1
d
1e
1e
2e
1, 00
l
r
nl
r
r
nl
l
l
ur
rc
EM cll
q
EMqV ur
Mcru
c












1
2
22
84
1e
r
nl l
cV
cV
q
E u
 









 














 


 



(35)

77 S. M. IKHDAIR
which is now amenable to the NU solution. We further
use the following ansätze in order to make the above
differential equation more compact

 

2
2
22 2
nl 2
1
23
, 2,
,
81,
2, 2
r
nl nl
zr eQc
Mc EEMc
g
QQ
gVl l
gV gV













 




(36)
Notice that 2.
nl
EMc The KG equation can then
be reduced to

  

2
2
22
2
22 2
2
1
d0,
1 d1
, 2,
l
nl nl
nl
AzBz C
qz duz
zqzdz zzqz
Aq Bqq
C

 













 




(37)
where




0,0,1 .rz

, or 00z 
Before proceeding, the
boundary conditions on the radial wave functions are:
l and is
finite. Comparing (37) with (13), we obtain values for
the set of parameters given in Section 2:
ur

0 or 1
l
ur z

1234 5
22 2
67
2
2
89 10
2
11 12
13
1, , 0,2
1, 2,
4
4
,1,2
2
4
1, ,
14
11
2
nl nl
nl nl
nl
q
cccqcc
cqc qq
q
cc c
q
cc
q
cq
2
,

 






 









 






 






(38)
and also the energy equation through (23) as



22
2
2,0, 1, 2,
42
4
nl
nn
n






 (39)
Making use of (36), the above equation can be rewrit-
ten as
 









22
22 23
24 2
22
2
23
2
1
2
2
,
8
14(1)
11
2
nl
nl
nl
nl
EMc
VV
McEcnw
cnw
EMcVV
EMcV
ll
wqqc




 





 






(40)
The energy nl is defined implicitly by (40) which is
a rather complicated transcendental equation having
many solutions for given values of n and l In the above
equation, let us remark that it is not difficult to conclude
that bound-states appear in four energy solutions; only
two energy solutions are valid for the particle
E
p
nl
EE


and the second one corresponds to the anti-particle en-
ergy a
nl
EE

 in the Eckart-type field.
Referring to the general parametric model in Section 2,
we turn to the calculation of the corresponding wave
functions. The explicit form of the weight function be-
comes
 


 
21
2
2
23
2
1,
11
22
w
p
nl
zz qz
EMcVV
pnw nw
c









 





(41)
which gives the first part of the wave functions in the
form of the Jacobi polynomials:



2,21 12 pw
nn
yz Pqz




12

(42)
Further, the second part of the wave functions can be
found as

1w
p
zz qz   (43)
Hence, the un-normalized wave functions expressed in
terms of the Jacobi polynomials read
 


2,2 1
1
wpw
p
lnl n
uzNzqzPqz

  (44)
and consequently the total radial part of the wave func-
tions expressed in terms of the hypergeometric functions
are


 


1/222
2
21
1
,2;21;
pw
Drr
lnl
r
Rr Nreqe
Fnnpw pqe


 


 (45)
where nl is a constant related to the normalization.
The relationship between the Jacobi polynomials and the
hypergeometric functions is given by
N


,
21
12,1; 1;
ab
n
P
qxFnnabax (46)
where



 
 

21
0
,;; !
k
k
kk
x
Fx kk

  



 

Now, in taking 23 ,VV

the energy Equation (40)
satisfying nl for the equally-mixed scalar and vector
Eckart-type potentials becomes
E



2
22
22
24 22
22
nl
nl
EMcV
McEcnw
cnw


 

(46)

S. M. IKHDAIR
78
and the wave functions:
 



 
2,2 1
2
2
2
11
11
2
wvw
v
lnl n
nl
uzNzqz Pqz
EMcV
vnw nw
c 

 



 



2,
(47)
or the total radial wave functions in (45) are


 


12 22
2
21
e1e
,2;21;
vw
Drr
lnl
r
Rr Nrq
Fnnvw vqe


 


 

(48)
where nl is a normalization factor. The results given
in (46) and (47) are consistent with those given in (15)
and (18) of [58].
N
Taking
1,q2,

  12 and 3 0VV 0,V

(34) has become the Hulthén potential. Hence, we find
bound state solutions for equally-mixed scalar and vector




Sr Vr Hulthén potentials in the KG theory with
any orbital angular quantum number and an arbitrary
dimension D,
l
 

 
2
0
24 21,
2
21
2
nl
nl
EMcV
cn
Mc Ecn
Dl






 




(49)
and

 




2,21
2
0
2
e1e 12
1
2
rr
lnl n
nl
uz NPz
EMcV
n
n
c











 

,
(50)
The Jacobi polynomial in the above equation can be
expressed in terms of the hypergeometric function:


 


12
21
e1e
,2;21;e
Drr
lnl
r
Rr Nr
Fnn



 
 


 (51)
where nl is a constant related to the normalization.
The above results are identical to those found recently by
[62,70].
N
In the non-relativistic limit, inserting the equally
mixed Eckart-type potentials (1) into the Schrödinger
equation gives





22
2
12
22 2
22
2
2
22
84(1)
d2e
d1e
21e 0
1e
lr
nl
r
r
l
r
MVll
ur ME
rq
MV qur
q










 














(52)
and further making use of the following definitions:

1
2
2
2
28
, 0 1,
2, 2
nl
nl nl
ME MV
El
TT
MV T
T



l

 

(53)
lead us to obtain the set of parameters and energy equa-
tion given before in (38) and (39) with .

  Incorpo-
rating the above equation and using (39), we find the
following energy eigenvalues:
 

22
2
22 2
1222
1
21
122
11
2
8 1112
2
nl
MV
Enw
Mnw
MV
wl














 






(54)
In addition, following procedures indicated in (41) -
(45), we obtain expressions for the radial wave functions:


 


11
11
12 22
2,2 12
e1e
12e,
p
w
Drr
lnl
pw r
n
Rr Nr
P


 





12
2
12
1
12
2
11
2
nl
pMEV
MV
nw nw


 












(55)
3.2. The Rosen-Morse-Type Model
Under the replacement of q by the Eckart-type
potential model (1) will become the Rosen-Morse-type
potential model given in (2) of Ref. [52]:
,q




2
12
12
,sec tanh
, 0
qq
VrqVhr Vr
VV
 


,
(56)
or alternatively [39,40,72]


22
12
2
2
e1
,4 1e
1e
rr
r
r
q
VrqVV q
q2
e










 (57)
We may rewrite the above equation in a form to in-
clude the Woods-Saxon potential,


2
12
22
2
2
32
e1
,4 1e
1e
e
1e
r
r
r
r
r
VrqVV q
q
q
Vq














(58)
Defining the parameters:

79 S. M. IKHDAIR
 



2
22 2
00
n0 2
1
2
3
,
08,
02,
02
nn
Mc EEMc
g
QQ
lgV
lgV
lgV











 
 

 




(59)
we can easily write the s-wave KG equation with


Sr

for the potential (58) as

Vr

  

2
2
22
2
22 2
0
2
0
1
dd 0,
1d
d1
, 2,
n
nnl
n
AzBz C
qz uz
zqzz
zzqz
Aq Bqq
C

 


























(60)
Following the steps of solution mentioned in the pre-
vious subsection, we may obtain values for the parame-
ters given in Section 2:
1234 5
22 2
607 0
2
2
80 9100
2
1112 0
13
1, , 0,
2
1, 2,
4
4
, 1, 2,
2
4
1, ,
14
11
2
nn
n
n
q
cccqc c
cqcq q
q
ccc
q
cc
q
cq

 

2
n





 









 




 


 














(61)
and the energy equation



22
2
02, 0, 1, 2,
42
4
n
n
n
n










(62)
Inserting (59) in the above equation, we obtain energy
equation satisfying
0, n
E









222
0
22 23
24 2
02
2
023
2
01
2
2
,
8
111
2
n
n
n
n
EMc VV
McEcn w
cnw
EMcVV
EMcV
w
qc



 
 













2
(63)
The corresponding un-normalized wave functions can
be calculated as before. The explicit form of the weight
function reads
 


 
21
2
2
023
2
1,
11
22
w
p
n
zz qz
EMcVV
pnw nw
c









 









(64)
which gives the Jacobi polynomials



2,21 12 pw
nn
yz Pqz





12
(65)
as the first part of the wave function. The second part of
the wave function can be found as

1w
p
zz qz  

 (66)
Hence, the un-normalized wave function reads



2,2 1
1
wpw
p
nnn
uzNzqz Pqz

 


 (67)
and thus the total radial part of the radial wave functions
in (30) can be expressed in terms of the hypergeometric
functions as

 

22
2
21
e1e
,2();21;e
pw
rr
nn
r
Rr Nq
Fnnpw pq





 


 
(68)
where is a normalization factor.
n
Taking 23
N

VV

in (63), we find the equation for the
potential in (56) satisfying in the s-wave KG the-
ory,
0n
E


 
24 2
0
2
22
0
22 2
22
n
n
Mc E
EMc V
cnw
cn



 



w
(69)
and the wave functions take the form



1
22
2
211 1
()e1 e
,2; 21;
pw
rr
nn
r
ur Nq
Fnnpw pqe





 


 
(70a)

 
2
02
12
11
,
2
n
EMcV
pnw nw
c 





 







(70b)
where n is a normalization constant. After the fol-
lowing mapping on the potential parameter: 11 VV
in (56), the results in (69) and (70) become identical with
(13) and (14) of [52].
N


Also, taking 1,q

2,

  and
12
0VV 30 ,VV


(58) turns to become the Woods-Saxon potential. Hence,
we can find bound state solutions in the s-wave KG the-
ory with equally-mixed scalar and vector




Sr Vr
for Woods-Saxon potentials as

S. M. IKHDAIR
80


2
0
24 20
022 2
, ,
2
n
n
EMc
V
n
McEcppn
c


   

(71)
and wave functions:




22
2,1
e12
pp
rr
nn n
ur NP
  



e,

e
r  
(72)
or alternatively, it can be expressed in terms of the hy-
pergeometric function as

 
2
2122
e,2; 21;
p
r
nn
RrNF nnpp
 


 (73)
where n is a constant related to the normalization.
Under appropriate parameter replacements, we obtain the
non-relativistic limit of the energy eigenvalues and ei-
genfunctions of the above two equations are
N
0
0
2
11
, 0,
22
n
MV
n
E
Mn



 



n
(74)
and

 

3
212 2
0
32
e,2; 21;
21,
2
p
rr
nn
urNF nnpp
MV
n
pn
c









e,
(75)
respectively, which is simply the solution of the
Schrödinger equation for the potential



rVr
The above results are identical to those
found before in [8].
 
2Sr Vr.
2

4. Discussions
In this section, at first, we choose appropriate parameters
in the Eckart-type potential model to construct the Eckart
potential, Rosen-Morse well and their PT-symmetric
versions, and then discuss their energy equations in the
framework of KG theory with equally mixed potentials.
4.1. Eckart Potential Model
Taking the potential (1) turns to the standard
Eckart potential [41]
1,q
 
2
121
coscoth, ,0VrVechrVrV V   (76)
In natural units (), we can obtain the energy
equation (46) for the Eckart potential in space
spinless KG theory as
1c 
3D


 

2
2
22
22 2
22
21
2
,
()
8
1
1121
2
nl
nl
nl
VEM
ME nwnw
EMV
wwq l




 



 
 


which is identical with those given in Equation (22) of
[52] under the equally-mixed potential restriction given
by




.Sr Vr The unnormalized wave function
corresponding to the energy levels is



 


12 22
2
21
e1e
,2; 21; e,
vw
Drr
lnl
r
Rr Nr
Fnn vw v



 



 
(78)
where is a normalization factor.
nl
1) For s-wave case, the centrifugal term
N





2
2123 40DlDlr


and hence


2
22 2
2123 e10
rr
DlDle




 
too. Thus, the energy eigenvalues take the following
simple form



2
2
220
22 2
01
22
1
01
12
,
()
8
111 .
2
n
n
n
VEM
ME nwnw
EMV
w










(79)
2) In the non-relativistic approximation of the KG en-
ergy equation (potential energies small compared to
2
M
c and EMc

Equation (32) reduces into the form
[72]
  


2
22
22
2
d(1)
2d
.
l
l
nl l
ur ll
VrSru r
Mrr
EMcur
 






(80)
When




,Vr Sr the energy spectrum obtained
from (80) reduces to those energy spectrum obtained
from the solution of the Schrödinger equation for the
sum potential




2r.rV In other words, the non-
relativistic limit is the Schrödinger-like equation for the
potential



2
2
12
22
2
1e
e
82
1e
1e
r
r
r
r
VV










.
This can be achieved by making the parameter re-
placements 2
R
EMM

 and ,
R
NR
EM E so
the non-relativistic limit of our results in (46) reduces to
,

(77)
 
22
2
22
22
2
2
2 1,
2
NR
MV
Enw
Mnw











(81)
and the corresponding wave functions in (48) become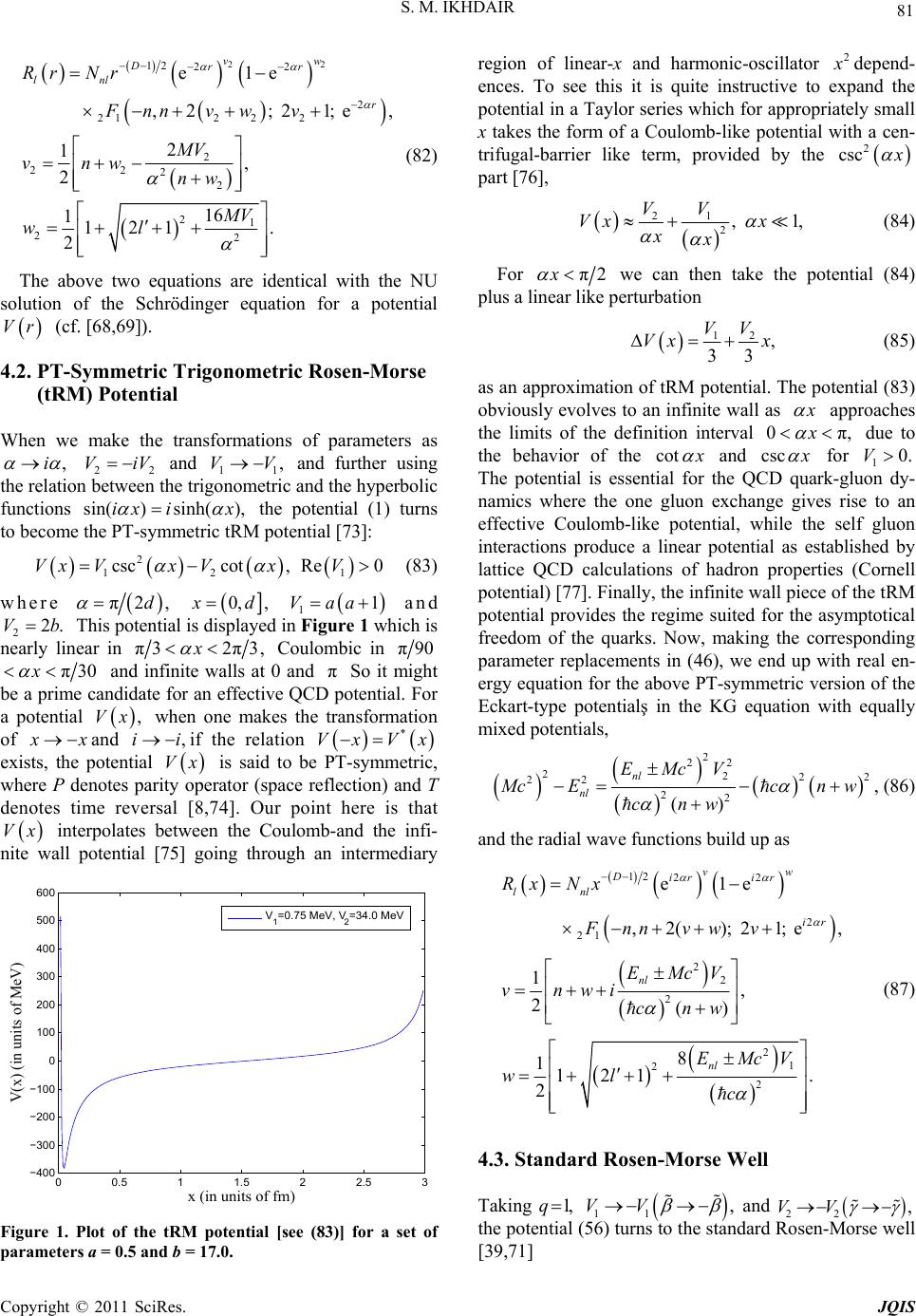

81 S. M. IKHDAIR









22
12 22
2
212 22
2
22
2
2
21
22
e1e
,2; 21; e,
2 1,
2
16 1121.
2
vw
Drr
lnl
r
Rr Nr
Fnn vwv
MV
vnw nw
MV
wl




 


 








 



(82)
The above two equations are identical with the NU
solution of the Schrödinger equation for a potential


Vr (cf. [68,69]).
4.2. PT-Symmetric Trigonometric Rosen-Morse
(tRM) Potential
When we make the transformations of parameters as
,i

  22 and 11 and further using
the relation between the trigonometric and the hyperbolic
functions
ViV
sin( )ix
,VV
), xsinh(i

  the potential (1) turns
to become the PT-symmetric tRM potential [73]:
 
2
12
csccot, Re0VxVx VxV   1  (83)
where

π2,d  


0, ,
x
d


11Vaa and
2 This potential is displayed in Figure 1 which is
nearly linear in
2.Vb
π32π3,x

 Coulombic in π90
πx30

 and infinite walls at 0 and So it might
be a prime candidate for an effective QCD potential. For
a potential when one makes the transformation
of
π

,Vx
x
x and if the relation ,ii



*
VxVx
exists, the potential is said to be PT-symmetric,
where P denotes parity operator (space reflection) and T
denotes time reversal [8,74]. Our point here is that
interpolates between the Coulomb-and the infi-
nite wall potential [75] going through an intermediary

Vx


Vx
0 0.5 1 1.52 2.5
3
−400
−300
−200
−100
0
100
200
300
400
500
600
x (in units of fm)
V(x) (in units of MeV)
V
1
=0.75 MeV, V
2
=34.0 MeV
Figure 1. Plot of the tRM potential [see (83)] for a set of
parameters a = 0.5 and b = 17.0.
region of linear-x and harmonic-oscillator 2
x
depend-
ences. To see this it is quite instructive to expand the
potential in a Taylor series which for appropriately small
x takes the form of a Coulomb-like potential with a cen-
trifugal-barrier like term, provided by the


2
ccs
x

part [76],
 
21
2, 1,
VV
Vx x
xx


  (84)
For π2x


we can then take the potential (84)
plus a linear like perturbation

12
,
33
VV
Vx x (85)
as an approximation of tRM potential. The potential (83)
obviously evolves to an infinite wall as
x

approaches
the limits of the definition interval 0π,x

 due to
the behavior of the cot
x

and csc
x

for 1
The potential is essential for the QCD quark-gluon dy-
namics where the one gluon exchange gives rise to an
effective Coulomb-like potential, while the self gluon
interactions produce a linear potential as established by
lattice QCD calculations of hadron properties (Cornell
potential) [77]. Finally, the infinite wall piece of the tRM
potential provides the regime suited for the asymptotical
freedom of the quarks. Now, making the corresponding
parameter replacements in (46), we end up with real en-
ergy equation for the above PT-symmetric version of the
Eckart-type potentialş in the KG equation with equally
mixed potentials,
0.V
 
 
2
22
2222
22
22,
()
nl
nl
EMcV
McEcn w
cnw



 



(86)
and the radial wave functions build up as


 






12 22
2
21
2
2
2
2
1
2
2
e1e
,2(); 21; e,
1,
2()
8
1121.
2
vw
Dir ir
lnl
ir
nl
nl
Rx Nx
Fnnvw v
EMcV
vnwi
cnw
EMcV
wl
c






 











 





(87)
4.3. Standard Rosen-Morse Well
Taking 1,q



11 ,VV

 

and


22 ,VV

  

the potential (56) turns to the standard Rosen-Morse well
[39,71]

S. M. IKHDAIR
82

2
212
sectanh, , 0.VrVhr VrVV   (88)


02
11
2
1
1,
2
n
EMV
n
n














 (90)
This potential is useful in discussing polyatomic mo-
lecular vibrational energies. An example of its applica-
tion to the vibrational states of NH₃ was given by Rosen
and Morse in [39,71]. Making the corresponding pa-
rameter replacements in Equation (69), we obtain the
energy equation for the Rosen-Morse well in the s-wave
KG theory with equally mixed potentials,
where n
N

 is a normalization constant. The results
given in (89) and (90) are consistent with those given in
(19) and (20) of [52], respectively. The s-wave energy
states of the KG equation for the Rosen-Morse potential
are calculated for a set of selected values parameters in
Table 1.



2
2
220
22 2
01
22
1
01
12
,
()
8
111 .
2
n
n
n
VE M
ME nn
EMV
 












(89)
When 00 ,VS

the non-relativistic limit is the solu-
tion of the Schrödinger equation for the potential



2
2
12
22
2
1e
e
82
1e
1e
r
r
r
r
VV











.
In the non-relativistic limits, the energy spectrum is
The un-normalized wave function corresponding to
the energy levels is
 
22
2
22
22
2
2
4
1,
2
NR
MV
En
Mn
 


















11
11
2,2 1
22 2
e1e 12e
rr
nn n
ur NP




 
  



,
r 
Table 1. The s-wave energy spectrum of the equally mixed scalar and vector Rosen-Morse-type potentials.
n α q V1 V2 M E1 E2 E3 E4
1 1 1 1 1 4 1.8137a –1.9140a –3.3923a –3.9088a
2 –2.2117 –3.6791
3 –0.6606 –3.3105
4 0.8879 –2.7697
5 1.8766 –1.9765
1 1 1 2 –2 5 0.9989 –3.7763 –4.7275 –4.9351
2 –4.1746 –4.7795
3 –3.3814 –4.5376
4 –2.3989 –4.2008
5 –1.3083 –3.7529
1 0.5 1 1 –1 4 1.9558 –3.5288 –3.8460 –3.9773
2 1.9608 –2.5367 –3.5326 –3.9216
3 1.2294 –0.5126 –3.0732 –3.8358
4 –2.4823 –3.7191
5 –1.7822 –3.5695
1 1 0.5 1 –1 4 1.5783 –3.2245 –3.6502 –3.9258
2 1.9995 –1.5367 –2.9520 –3.7496
3 –1.9529 –3.4736
4 –0.7335 –3.0839
5 0.5489 –2.5528
aThe present results are identical to the ones given in [52].

83 S. M. IKHDAIR
1
22
16 111
2
MV






,


(91)
and the wave functions are

 



22
22
2,2 1
22
2
2
22
2
2
e1e
12e,
2 1.
2
rr
nn n
r
Rr NP
MV
n
n
























(92)
5. Conclusions and Outlook
A parametric generalization short-cut derived from the
NU have been used to carry out the analytic bound states
(real energy spectrum and wave functions) of the KG
equation with any orbital quantum number l for equally
mixed scalar and vector Eckart-type potentials. The pre-
sent solutions include energy equation and un-normal-
ized wave functions which have been expressed in terms
of the Jacobi polynomials (or hypergeometric functions).
Additionally, in making appropriate changes in the Eckart-
type potential parameters, one can easily generate new
energy spectrum formulas for various types of the well-
known molecular potentials such as the Rosen-Morse
well [39], the Eckart potential, the Hulthén potential [13],
the Woods-Saxon potential [7] and the Manning-Rosen
potential [31] and others. It is also noted that under the
PT-symmetry property, the exponential potentials can be
reduced to the trigonometric potentials with real bound
state solutions. Also, the KG equation with equally
mixed scalar and vector Rosen-Morse-type potentials can
be solved exactly for s-wave bound states ( case).
The calculated energy equations of these potentials are
seen to be complicated transcendental equations in the
relativistic model [39]. The non-relativistic limit can be
easily reached by making a mapping on the parameters
and/or solving the original Schrödinger equation. It is
found that the relativistic and non-relativistic results are
identical with those ones obtained in literature through
the various methods.
0l
6. Acknowledgements
The author thanks the kind referees for their invaluable
suggestions which greatly helped in improving the
manuscript.
7. References
[1] L. I. Schiff, “Quantum Mechanics,” 3rd Edition,
McGraw-Hill, New York, 1955.
[2] L. D. Landau and E. M. Lifshitz, “Quantum Mechanics,
Non-Relativistic Theory,” 3rd. Edition, Pergamon, Ox-
ford, 1977.
[3] C. L. Pekeris, “The Rotation-Vibration Coupling in Dia-
tomic Molecules,” Physical Review, Vol. 45, 1934, pp.
98-103. doi:10.1103/PhysRev.45.98
[4] O. Bayrak and I. Boztosun, “Arbitrary -State Solutions
of the Rotating Morse Potential by the Asymptotic Itera-
tion Method,” Journal of Physics A: Mathematical and
General, Vol. 39, No. 22, 2006, pp. 6955-6964.
doi:10.1088/0305-4470/39/22/010
[5] W.C. Qiang and S. H. Dong, “Arbitrary l-State Solution-
sof the Rotating Morse potential Through the Exact
Quantization Method,” Physics Letters A, Vol. 363, No.3,
2007, pp. 169-176.
doi:10.1016/j.physleta.2006.10.091
[6] S. M. Ikhdair, “An Approximate  State Solutions of
the Dirac Equation for the Generalized Morse Potential
under Spin and Pseudospin Symmetry,” Journal of
Mathematical Physics, Vol. 52, No. 5, 2011, pp. 052303-
052322. doi:10.1063/1.3583553
[7] S. M. Ikhdair and R. Sever, “Any -State Solutions of
the Woods-Saxon Potential in Arbitrary Dimension
within the New Improved Quantization Rule,” Interna-
tional Journal of Modern Physics A, Vol. 25, No. 20,
2010, pp. 3941-3952. doi:10.1142/S0217751X10050160
[8] S. M. Ikhdair and R. Sever, “Exact Solution of the
Klein-Gordon Equation for the PT-Symmetric General-
ized Woods-Saxon Potential by the Nikiforov-Uvarov
Method,” Annals of Physics (Le ibz ig), Vol. 16, No. 3,
2007, pp. 218-232. doi:10.1002/andp.200610232
[9] S. M. Ikhdair and R. Sever, “Approximate Eigenvalue
and Eigen Function Solutions for the Generalized
Hulthén Potential with any Angular Momentum,” Journal
of Mathematical Chemistry, Vol. 42, No. 3, 2007, pp.
461- 471. doi:10.1007/s10910-006-9115-8
[10] C. Y. Chen, D. S. Sun and F. L. Lu, “Approximate Ana-
lytical Solutions of Klein-Gordon Equation with Hulthén
Potentials for Nonzero Angular Momentum,” Physics
Letters A, Vol. 370, No. 3-4, 2007, pp. 219-221;
doi:10.1016/j.physleta.2007.05.079
[11] W. C. Qiang, R. S. Zhou and Y. Gao, “Any -State
Solutions of the Klein-Gordon with the Generalized
Hulthén Potential,” Physics Letters A, Vol. 371, No. 3,
2007, pp. 201-204; doi:10.1016/j.physleta.2007.04.109
[12] S. Dong, S.-H. Dong, H. Bahlouli and V. B. Bezzerra,
“Algebraic Approach to the Klein-Gordon Equation with
Hyperbolic Scarf Potential,” International Journal of
Modern Physics E, Vol. 20, No.1, 2011, pp. 55-61.
doi:10.1142/S0218301311017326
[13] S. M. Ikhdair and J. Abu-Hasna, “Quantization Rule So-
lution to the Hulthén Potential in Arbitrary Dimension
with a New Approximate Scheme for the Centrifugal
Term,” Physica Scripta, Vol. 83, No.2, 2011, pp.
025002-7. doi:10.1088/0031-8949/83/02/025002

S. M. IKHDAIR
84
[14] G.-F. Wei, Z.-Z. Zhen and S.-H. Dong, “The Relativistic
Bound and Scattering States of the Manning-Rosen Po-
tential with an Improved New Approximate Scheme to
the Centrifugal Term,” Central European Journal of
Physics, Vol. 7, No. 1, 2009, pp. 175-183.
doi:10.2478/s11534-008-0143-9
[15] S.M. Ikhdair and R. Sever, “Approximate Bound State
Solutions of Dirac Equation with Hulthén Potential In-
cluding Coulomb-Like Tensor Potential,” Applied Mathe-
matics and Computation, Vol. 216, No. 3, 2010, pp. 911-
923. doi:10.1016/j.amc.2010.01.104
[16] S. Flügge, “Practical Quantum Mechanics,” Vol. 1,
Springer, Berlin, 1994.
[17] J. Y. Guo, J. Meng and F. X. Xu, “Any -State Solu-
tions of the Klein-Gordon Equation with Special Hulthén
Potentials,” Chiniese Physics Letters, Vol. 20, 2003, pp.
602-604.
[18] A. D. Alhaidari, “Solution of the Relativistic Dirac-Hul-
then Problem,” Journal of Physics A, Vol. 37, 2004, pp.
5805-5813. doi:10.1088/0305-4470/37/22/007
[19] O. Bayrak, G. Kocak and I. Boztosun, “Any -State
Solutions of the Hulthén Potential by the Asymptotic It-
eration Method,” Journal of Physics A: Mathematical and
General, Vol. 39, 2006, pp. 11521-11529.
doi:10.1088/0305-4470/39/37/012
[20] S. Haouat and L. Chetouani, “Approximate Solutions of
Klein-Gordon and Dirac Equations in the Presence of the
Hulthén Potential,” Physica Scripta, Vol. 77, 2008, pp.
025005-6; doi:10.1088/0031-8949/77/02/025005
[21] E. Olğar, R. Koç and H. Tütüncüler, “The Exact Solution
of the s-Wave Klein-Gordon Equation for the General-
ized Hulthén Potential by the Asymptotic Iteration
Method,” Physica Scripta, Vol. 78, 2008, pp. 015011-4;
[22] C. S. Jia, J. Y. Liu and P. Q. Wang, “A New Approxima-
tion Scheme for the Centrifugal Term and Hulthén Poten-
tial,” Physics Letters A, Vol. 372, 2008, pp. 4779-4782.
[23] S.-H. Dong, “A New Quantization Rule to the Energy
Spectra for Modified Hyperbolic-Type Potentials,” In-
ternational Journal of Quantum Chemistry, Vol. 109, No.
4, 2009, pp. 701-707. doi:10.1002/qua.21862
[24] M. F. Manning, “Exact Solutions of the Schrödinger
Equation,” Physical Review, Vol. 48, 1935, pp. 161-164.
doi:10.1103/PhysRev.48.161
[25] A. Diaf, A. Chouchaoui and R. L. Lombard, “Feynman
Integral Treatment of the Bargmann Potential,” Annals of
Physics, Vol. 317, 2005, pp. 354-365.
doi:10.1016/j.aop.2004.11.010
[26] G.-F. Wei, C.-Y. Long and S.-H. Dong, “The Scattering
of the Manning- Rosen Potential with Centrifugal Term,”
Physics Letters A, Vol. 372, No. 15, 2008, pp. 2592-2596.
doi:10.1016/j.physleta.2007.12.042
[27] S.-H. Dong and J. Garcia-Ravelo, “Exact Solutions of the
s-Wave Schrödinger Equation with Manning-Rosen Po-
tential,” Physica Scripta, Vol. 75, 2007, pp. 307-309.
doi:10.1088/0031-8949/75/3/013
[28] W.-C. Qiang and S. H. Dong, “Analytical Approximation
to the Solutions of the Manning-Rosen Potential with
Centrifugal Term,” Physics Letters A, Vol. 368, No.1-2,
2007, pp. 13-17. doi:10.1016/j.physleta.2007.03.057
[29] W.-C. Qiang and S.-H. Dong, “The Manning-Rosen Po-
tential Studied by a New Approximate Scheme to the
Centrifugal Term,” Physica Scripta, Vol. 79, No. 4, 2009,
p. 045004. doi:10.1088/0031-8949/79/04/045004
[30] C. Y. Chen, F. L. Lu and D. S. Sun, “Exact Solutions of
Scattering States for the s-Wave Schrödinger Equation
with the Manning-Rosen Potential,” Physica Scripta, Vol.
76, 2007, pp. 428-430. doi:10.1088/0031-8949/76/5/003
[31] S. M. Ikhdair, “On the Bound-State Solutions of the Man-
ning-Rosen Potential Including an Improved Approxima-
tion to the Orbital Centrifugal Term,” Physica Scripta,
Vol. 83, 2011, pp. 015010-10.
doi:10.1088/0031-8949/83/01/015010
[32] E. Olğar, R. Koç and H. Tütüncüler, “Bound States of the
s-Wave Equation with Equal Scalar and Vector Standard
Eckart Potential,” Chinese Physics Letters, Vol. 23, 2006,
pp. 539-541. doi:10.1088/0256-307X/23/3/004
[33] W.-C. Qiang, J.-Y. Wu and S.-H. Dong, “The Eckart-
Like Potential Studied by a New Approximate Scheme to
the Centrifugal Term,” Physica Scripta, Vol. 79, No. 6,
2009, p. 065011. doi:10.1088/0031-8949/79/06/065011
[34] X. Zou, L. Z. Yi and C. S. Jia, “Bound States of the Dirac
Equation with Vector and Scalar Eckart Potentials,”
Physics Letters A, Vol. 346, 2005, pp. 54-64.
doi:10.1016/j.physleta.2005.07.075
[35] G.-F. Wei, S.-H. Dong and V. B. Bezerra, “The Relativ-
istic Bound and Scattering States of the Eckart Potential
with a Proper New Approximate Scheme for the Cen-
trifugal Term,” International Journal of Modern Physics
A, Vol. 24, No. 1, 2009, pp. 161-172.
doi:10.1142/S0217751X09042621
[36] C. S. Jia, P. Guo and X. L. Peng, “Exact Solutions of the
Dirac-Eckart Problem with Spin and Pseudospin Symme-
try,” Journal of Physics A: Mathematical and Theoretical,
Vol. 39, No. 24, 2006, pp. 7737-7744.
doi:10.1088/0305-4470/39/24/010
[37] S. H. Dong, W. C. Qiang, G. H. Sun and V. B. Bezerra,
“Analytical Approximations to the -Wave Solutions of
the Schrödinger Equation with the Eckart Potential,”
Journal of Physics A: Mathematical and Theoretical, Vol.
40, No. 34, 2007, pp. 10535-10540.
doi:10.1088/1751-8113/40/34/010
[38] W.-C. Qiang and S.-H. Dong, “Analytical Approximation
to the -Wave Solutions of the Klein-Gordon Equation
for a Second Pöschl-Teller Like Potential,” Physics Let-
ters A, Vol. 372, No. 27-28, 2008, pp. 4789-4792.
doi:10.1016/j.physleta.2008.05.020
[39] S. M. Ikhdair, “Approximate Solutions of the Dirac Equa-
tion for the Rosen-Morse Potential Including the
Spin-Orbit Centrifugal Term,” Journal of Mathematical
Physics, Vol. 51, No. 2, 2010, pp. 023525-16;
doi:10.1063/1.3293759
[40] G.-F. Wei and S.-H. Dong, “Pseudospin Symmetry for
Modified Rosen-Morse Potential Including a Pekeris-

85 S. M. IKHDAIR
Type Approximation to the Pseudo-Centrifugal Term,”
The European Physical Journal A, Vol. 46, No. 2, 2010,
pp. 207-212. doi:10.1140/epja/i2010-11031-0
[41] C. Eckart, “The Penetration of a Potential Barrier by
Electrons,” Physics Review, Vol. 35, No. 11, 1930, pp.
1303-1309. doi:10.1103/PhysRev.35.1303
[42] F. Cooper, A. Khare and U. Sukhatme, “Supersymmetry
and Quantum Mechanics,” Physics Report, Vol. 251, No.
5-6, 1995, pp. 267-385.
doi:10.1016/0370-1573(94)00080-M
[43] J. J. Weiss, “Mechanism of Proton Transfer in Acid-Base
Reactions,” Journal of Chemical Physics, Vol. 41, 1964,
pp. 1120-1124. doi:10.1063/1.1726015
[44] A. Cimas, M. Aschi, C. Barrientos, V. M. Rayőn, J. A.
Sordo and A. Largo, “Computational Study on the Kinet-
ics of the Reaction of


4
N
Swith 2 CHF ,” Chemical
Physics Letters , Vol. 374, No. 5-6, 2003, pp. 594-600.
doi:10.1016/S0009-2614(03)00771-1
[45] C. S. Jia, X. L. Zeng and L. T. Sun, “PT Symmetry and
Shape Invariance for a Potential Well with a Barrier,”
Physics Letters A, Vol. 294, No. 3-4, 2002, pp. 185-189.
doi:10.1016/S0375-9601(01)00840-4
[46] C. S. Jia, Y. Li, Y. Sun, J. Y. Liu and L. T. Sun, “Bound
States of the Five Parametric Exponential-Type Potential
Model,” Physics Letters A, Vol. 311, No. 2-3, 2003, pp.
115-125. doi:10.1016/S0375-9601(03)00502-4
[47] H. Eğrifes, D. Demirhan and F. Büyükkılıç, “Exact Solu-
tions of the Schrödinger Equation for Two Deformed
Hyperbolic Molecular Potentials,” Physica Scripta, Vol.
60, No.3, 1999, pp. 195-198.
doi:10.1238/Physica.Regular.060a00195
[48] A. Arai, “Exactly Solvable Supersymmetric Quantum
Mechanics,” Journal of Mathematical Analysis and Ap-
plications, Vol. 158, No.1, 1991, pp. 63-79.
doi:10.1016/0022-247X(91)90267-4
[49] R. Dutt, A. Khare and U. Sukhatme, “Supersymmetry,
Shape Invariance, and Exactly Solvable Potentials,”
American Journal of Physics, Vol. 56, No.2, 1988, pp.
163-168. doi:10.1119/1.15697
[50] R. De, R. Dutt and U. Sukhatme, “Mapping of Shape
Invariant Potentials Under Point Canonical Transforma-
tions,” Journal of Physics A: Mathematical and General,
Vol. 25, No. 13, 1992, pp. L843-L850.
doi:10.1088/0305-4470/25/13/013
[51] M. Hruska, W.Y. Keung and U. Sukhatme, “Accuracy of
semi classical Methods for Shape-Invariant Potentials,”
Physics Review A, Vol. 55, No. 5, 1997, pp. 3345-3350.
doi:10.1103/PhysRevA.55.3345
[52] L.Z. Yi, Y.F. Diao, J.Y. Liu and C.S. Jia, “Bound States
of the Klein-Gordon Equation with Vector and Scalar
Rosen-Morse-Type Potentials,” Physics Letters A, Vol.
333, 2004, pp. 212-217.
doi:10.1016/j.physleta.2004.10.054
[53] R.L. Greene and C. Aldrich, “Variational Wave Func-
tions for a Screened Coulomb Potential,” Physics Review
A, Vol. 14, 1976, pp. 2363-2366.
doi:10.1103/PhysRevA.14.2363
[54] G. F. Wei, C. Y. Long, X. Y. Duan and S. H. Dong, “Ar-
bitrary -Wave Scattering State Solutions of the
Schrödinger Equation for the Eckart Potential,” Physica
Scripta, Vol. 77, 2008, pp. 035001-5.
doi:10.1088/0031-8949/77/03/035001
[55] C. Y. Chen, D. S. Sun and F.L. Lu, “Analytical Ap-
proximations of Scattering States to the -Wave Solu-
tions for the Schrödinger Equation with the Eckart Poten-
tial,” Journal of Physics A: Mathematical and Theoretical,
Vol. 41, No. 3, 2008, pp. 035302.
doi:10.1088/1751-8113/41/3/035302
[56] A. Soylu, O. Bayrak and I. Boztosun, “  -State Solutions
of the Dirac Equation for the Eckart Potential with Pseu-
dospin- and Spin-Symmetry,” Journal of Physics A:
Mathematical and Theoretical, Vol. 41, 2008, pp.
065308-8. doi:10.1088/1751-8113/41/6/065308
[57] L. H. Zhang, X. P. Li and C. S. Jia, “Analytical Ap-
proximation to the Solution of the Dirac Equation with
the Eckart Potential Including the Spin-Orbit Coupling
Term,” Physics Letters A, Vol. 372, 2008, pp. 2201-2207.
doi:10.1016/j.physleta.2007.11.022
[58] Y. Zhang, “Approximate Analytical Solutions of the
Klein-Gordon Equation with scalar and Vector Eckart
Potentials,” Physica Scripta, Vol. 78, 2008, pp. 015006-4.
doi:10.1088/0031-8949/78/01/015006
[59] C. S. Jia, J. Y. Liu and P. Q. Wang, “A New Approxima-
tion Scheme for the Centrifugal Term and the Hulthén
Potential,” Physics Letters A, Vol. 372, No. 27-28, 2008,
pp. 4779-4782. doi:10.1016/j.physleta.2008.05.030
[60] A. F. Nikiforov and V. B. Uvarov, “Special Functions of
Mathematical Physics,” Birkhauser, Bassel, 1988.
[61] S. M. Ikhdair and R. Sever, “Exact Quantization Rule to
the Kratzer-Type Potentials: An Application to the Dia-
tomic Molecules,” Journal of Mathematical Chemistry,
Vol. 45, No. 4, 2009, pp. 1137-1152.
doi:10.1007/s10910-008-9438-8
[62] S. M. Ikhdair and R. Sever, “Solutions of the Spatially-
Dependent Mass Dirac Equation with the Spin and Pseu-
dospin Symmetry for the Coulomb-Like Potential,” Ap-
plied Mathematics and Computation, Vol. 216, No. 2,
2010, pp. 545-555. doi:10.1016/j.amc.2010.01.072
[63] S. M. Ikhdair, C. Berkdemir and R. Sever, “Spin and
Pseudospin Symmetry Along With Orbital Dependency
of the Dirac- Hulthén Problem,” Applied Mathematics
and Computation, Vol. 217, No. 22, 2011, pp. 9019-9032.
doi:10.1016/j.amc.2011.03.109
[64] S. M. Ikhdair and R. Sever, “Bound-States of a Semi-
Relativistic Equation for the PT-Symmetric Generalized
Potential by the Nikiforov-Uvarov Method,” International
Journal of Modern Physics E, Vol. 17, No. 6, 2008, pp.
1107-1123.
doi:10.1142/S0218301308010337
[65] A. de Souza Dutra and G. Chen, “On Some Classes of
Exactly-Solvable Klein-Gordon Equations,” Physics Let-
ters A, Vol. 349, 2006, pp. 297-301.
doi:10.1016/j.physleta.2005.09.056

S. M. IKHDAIR
86
[66] G. Chen, “Solutions of the Klein-Gordon for Exponential
Scalar and Vector Potentials,” Physics Letters A, Vol. 339,
2005, pp. 300-303. doi:10.1016/j.physleta.2005.03.040
[67] S. M. Ikhdair, “Rotation and Vibration of Diatomic
Molecule in the Spatially-Dependent Mass Schrodinger
Equation with Generalized q-Deformed Morse Potential,”
Chemical Physics, Vol. 361, No. 1-2, 2009, pp. 9-17.
doi:10.1016/j.chemphys.2009.04.023
[68] N. Saad, “The Klein-Gordon Equation with a Generalized
Hulthén Potential in D-Dimensions,” Physica Scripta,
Vol. 76, 2007, pp. 623-627.
doi:10.1088/0031-8949/76/6/005
[69] W. C. Qiang, R. S. Zhou and Y. Gao, “Any -State
Solutions of the Klein-Gordon Equation with the Gener-
alized Hulthén Potential,” Physics Letters A, Vol. 371,
No. 3, 2007, pp. 201-204.
doi:10.1016/j.physleta.2007.04.109
[70] S. M. Ikhdair and R. Sever, “Any -State Improved
Quasi-Exact Analytical Solutions of the Spatially De-
pendent Mass Klein-Gordon Equation for the Scalar and
Vector Hulthén Potentials,” Physica Scripta, Vol. 79, No.
3, 2009, pp. 035002-12.
doi:10.1088/0031-8949/79/03/035002
[71] N. Rosen and P. M. Morse, “On the Vibrations of Polya-
tomic Molecules,” Physics Review, Vol. 42, No. 2, 1932,
pp. 210-217. doi:10.1103/PhysRev.42.210
[72] A. S. de Castro, “Klein-Gordon Particles in Mixed Vec-
tor-Scalar Inversely Linear Potentials,” Physics Letters A,
Vol. 338, 2005, p. 81. doi:10.1016/j.physleta.2005.02.027
[73] F. Cooper, A. Khare and U. P. Sukhatme, “Supersym-
metry in Quantum Mechanics,” World Scientific, Singa-
pore, 2001.
[74] C. M. Bender and S. Boettcher, “Real Spectra in Non-
Hermitian Hamiltonians Having PT Symmetry,” Physical
Review Letters, Vol. 80, No. 24, 1998, pp. 5243-5246.
doi:10.1103/PhysRevLett.80.5243
[75] C. B. C. Jasso, “Baryon Spectra in a Quark-Diquark
Model with the Trigonometric Rosen- Morse Potential,”
MS Thesis (in Spanish), Institute of Physics, Autonomous
University of San Luis Potosi, México, 2005.
[76] M. R. Spiegel, “Mathematical Handbook of Formulas and
Tables,” McGraw-Hill Publishing Company, New York,
1968.
[77] E. Eichten, K. Gottfried, T. Kinoshita, K.D. Lane and
T.M. Yan, “Charmonium: Comparison with Experiment,”
Physical Review D, Vol. 21, No. 1, 1980, pp. 203-233.
doi:10.1103/PhysRevD.21.203