Open Access Library Journal
Vol.04 No.05(2017), Article ID:76181,11 pages
10.4236/oalib.1103593
3D Matrix Ring with a “Common” Multiplication
Orgest Zaka
Department of Mathematics, Faculty of Technical Science, University of Vlora “Ismail QEMALI”, Vlora, Albania

Copyright © 2017 by author and Open Access Library Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 11, 2017; Accepted: May 12, 2017; Published: May 15, 2017
ABSTRACT
In this article, starting from geometrical considerations, he was born with the idea of 3D matrices, which have developed in this article. A problem here was the definition of multiplication, which we have given in analogy with the usual 2D matrices. The goal here is 3D matrices to be a generalization of 2D matrices. Work initially we started with
matrix, and then we extended to
matrices. In this article, we give the meaning of 3D matrices. We also defined two actions in this set. As a result, in this article, we have reached to present 3-dimensional unitary ring matrices with elements from a field F.
Subject Areas:
Algebra, Applied Statistical Mathematics, Geometry
Keywords:
Linear Algebra, Matrices, Ring Theory

1. Introduction
Based on the meaning of the addition and the multiplication of 2D matrices [1] - [6] , this article stretches this sense, the idea, the addition and the multiplication of 3D matrices. Starting from geometrical considerations, concretely taking into account the cube, he was born with the idea of 3D matrices, which have developed in this article. A problem here was the definition of multiplication, for which we have acted pages, analogously acted as the columns, which we have given in analogy with the usual 2D matrices [6] [9] . The goal here is 3D matrices to be a generalization of 2D matrices. We proved that this set of two actions together in forming the “unitary ring” [7] [8] [10] [11] . In literature and in various mathematical forums, we noticed an interest in the 3D matrices, but on the other hand are missing results associated with them; this was a sufficient reason to explore. We introduced the meaning of the scalar multiplication, and finally we have shown that we have an F-module connected to this ring 3D matrices or vector spaces [8] [10] . As indications for this paper were simply geometric imaginations. Everything presented in this article are my results.
2. Addition of 3 × 3 × 3, 3-D Matrices over Field F, and the Addition Abelian Group of Their 3-D Matrices
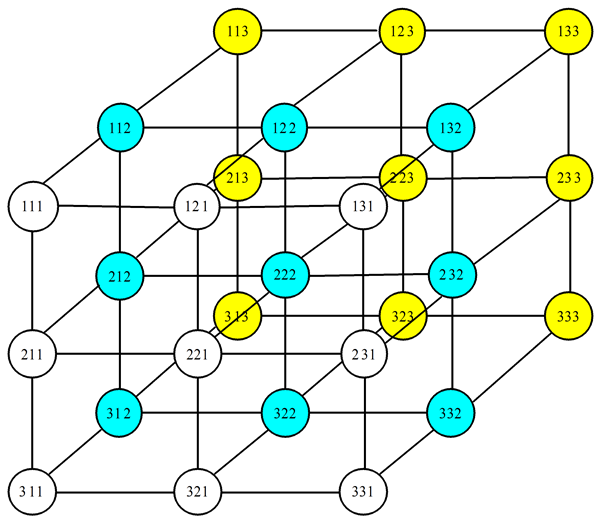
Imagining a parallelepiped, with born idea of 3D matrices, which are define as follows
Definition 2.1 3-dimensional 3 × 3 × 3 matrice will call, a matrix which has: three horizontal layers (analogous to three rows), three vertical page (analogue with three columns in the usual matrices) and three vertical layers two of which are hidden.
The set of these matrices the write how:
The appearance of these matrices will be as in Figure 1.
Definition 2.2 The addition of two matrices
we will call the matrix:
The appearance of the addition of 3 × 3 × 3, 3D matrices, will be as in Figure 2, where matrices A and B have the following appearance,
![]()
Figure 2. The addition of 3 × 3 × 3, 3D matrices.
Definition 2.3 Zero matrix 3 × 3, 3D we will called the matrix that has all its elements zero.
Definition 2.4. The opposite matric of anmatrice
will, called matrix
(where
is a opposite element of element
, so
and
is field [8] [10] [11] ), which satisfies the condition
Theorem 2.1
is a beliangrup.
Proof: Truly from the definition 2.2, of addition the 3-Dmatrices, we see that addition is the sustainable in
, because
1) Associative property,
truly
2)
truly,
3)
truly, from Definition 2.4, we have
4) Addition is commutative.
truly
3. Addition of
, 3-D Matrices over Any Field F and the Addition Abelian Group of Their 3-D Matrices
Definition 3.1 3-dimensionalmxnxp matrix will call, a matrix which has: m- horizontal layers (analogous to m-rows), n-vertical page (analogue with n-col- umns in the usualmatrices) and p-vertical layers (p − 1 of which are hidden).
The set of these matrixes the write how:
Definition 3.2 The addition of two matrices
we will call the matrix:
The appearance of the addition of mxnxp, 3D matrices will be as in Figure 3, where matrices A and B have the following appearance,
Definition 3.3 3-D, Zero matrix
, we will called the matrix that has all its elements zero.
Definition 3.4 The opposite matric of anmatrice
will, called matrix
![]()
Figure 3. The addition of mxnxp, 3D matrices.
(where
is a opposite element of element
, so
and
is field), which satisfies the condition
Theorem 3.1
is abeliangrup.
Proof: Truly from the definition 3.2, of additions the 3-D matrices, we see that addition is the sustainable in
, because
1) Associative property,
truly
2)
truly,
3)
truly, from Definition 2.4, we have
4) Addition is commutative.
truly
4. The “Common” Multiplication of
, 3-D Matrices with Elements Froman Field F
Definition 4.1: The multiplication of two matrices
we will call the matrix
calculated as follows:
The appearance of the multiplication of 3 × 3 × 3, 3D matrices will be as in Figure 4.
where, the first vertical page is:
![]()
Figure 4. The multiplication of 3 × 3 × 3, 3D matrices.
the second vertical page is:
and third vertical page is:
It is reduce the above notes through matrix blocks
where
and
Remark 4.1 Two dimensional matrices can think like matrix with size
Easy seen from the definition 1, above it that, if
and
we get, the usual 3 × 3-matrix multiplication, then will take only the first vertical layer is (or, in the language of matrix blocks would say that:
;
;
;
):
Definition 4.2. The3-D,unit matrix, associated with the “common” multiplication, must be:
or, in the language of matrix blocks:
Easy distinguish that,
Theorem 4.1
is a unitary semi-Group with regard to this ordinary multiplication
Proof: 1) associative property.
2)
Theorem 4.2
is a unitary Ring.
Proof: 1) From Theorem 2.1.
is abeliangrup.
2) From Theorem 4.1.
is a unitary semi-Group, and consequently also,
is a unitary semi-Group
3)
truly
In a similar manner proved the point (b).
5. Multiplication of a 3-D,
-Matrix by a Scalar
Definition 5.1 The multiplication of matrix
with scalar
, is matrix
:
So
Theorem 5.1
is a vector space
Proof. is evident because,
it is the vector space, see [6] [8] [9] [10] .
Definition 5.2 The multiplication of matrix
with scalar
, is matrix
:
wherein each element of the matrix is multiplied (by multiplication of the field F) with the element
. Well, so we have
Theorem 5.2
is a vector space
Proof. Is evident because,
it is the vector space, see [6] [8] [9] [10]
6. Conclusion
In this article, based on geometric considerations, and mostly considering the cube, we managed to develop the idea of the 3D matrix doing so a generalization of the 2D matrices, step by step. Furthermore, we gave a unitary ring with the elements of a field F. Initially we gave the ring
, 3D matrices and then generalized this concept for
, 3D matrices. At the end of this article, we present the scalar multiplication with the 3D matrices and we show that the set of
, 3D matrix, forms a vector space over the field F.
Cite this paper
Zaka, O. (2017) 3D Matrix Ring with a “Common” Multipli- cation. Open Access Library Journal, 4: e3593. https://doi.org/10.4236/oalib.1103593
References
- 1. Artin, M. (1991) Algebra. Prentice Hall, Upper Saddle River.
- 2. Bretscher, O. (2005) Linear Algebra with Applications. 3rd Edition, Prentice Hall, Upper Saddle River.
- 3. Connell, E.H. (2004) Elements of Abstract and Linear Algebra.
- 4. Schneide, H. and Barker, G.P. (1973) Matrices and Linear Algebra (Dover Books on Mathematics). 2nd Revised Edition.
- 5. Lang, S. (1987) Linear Algebra. Springer-Verlag, Berlin, New York.
- 6. Nering, E.D. (1970) Linear Algebra and Matrix Theory. 2nd Edition, Wiley, New York.
- 7. Zaka, O. and Filipi, K. (2016) The Transform of a Line of Desargues Affine Plane in an Additive Group of Its Points. International Journal of Current Research, 8, 34983-34990.
- 8. Zaka, O. (2013) Abstract Algebra II. Vllamasi, Tirana.
- 9. Zaka, O. (2013) Linear Algebra I. Vllamasi, Tirana.
- 10. Zaka, O. (2013) Linear Algebra II. Vllamasi, Tirana.
- 11. Zaka, O. and Filipi, K. (2016) One Construction of an Affine Plane over a Corps. Journal of Advances in Mathematics, 12.