Journal of Biomedical Science and Engineering
Vol.10 No.05(2017), Article ID:76089,10 pages
10.4236/jbise.2017.105B003
Connective Tissue Energy Loss Comparison between Joints with and without Hypermobility
Stephen A. Tatarkov, Angela C. Tesny, Brittany M. Lauck, Louis A. DiBerardino III, Hui Shen*
Mechanical Engineering, Ohio Northern University, Ada, OH, USA
Email: *h-shen@onu.edu



Received: March 3, 2017; Accepted: May 3, 2017; Published: May 10, 2017
ABSTRACT
Joint hypermobility syndrome is a condition in which a joint can move effortlessly beyond the normal limit of motion expected for that joint. This syndrome is affected by some factors including gender and tends to be inherited. It may cause some symptoms such as pain in an individual’s synovial joints. The objective of the current study was to compare the energy loss of connective tissues between joints with and without hypermobility. A differential equation model, namely the Kelvin-Voigt model, was used for the energy loss analysis. The results show the difference in energy loss for the tissues attached to joints with and without joint hypermobility. As the stiffness of the connective tissue decreases, the energy loss increases. Muscle activity about the ankle was measured via electromyography during simple functional tasks, and the recorded data were used to correlate with the theoretical analysis of the energy loss. The result would shed light on the pathology analysis of the symptoms such as the cause of pain.
Keywords:
Joint Hypermobility Syndrome, Soft Connective Tissues, Electromyography, Kelvin-Voigt Model

1. Introduction
Joint hypermobility is a condition in which a joint can move effortlessly beyond the normal limit of motion expected for that joint. It has been reported that hypermobile joints can be inherited or obtained by stretching or exercising over a period of time [1] [2] [3]. For some people with hypermobile joints, it can be considered a benign condition and even as an advantage in some professions [3]. However, for less fortunate people with such joints, they may suffer some symptoms such as pain and weakness and have to seek medical treatment [4]. Hypermobility may cause problems including arthritis, internal joint derangements, and soft tissue injuries [5] [6] [7]. For the hypermobile joints with symptoms, it is usually called joint hypermobility syndrome (JHS) [3].
Joint hypermobility is quite prevalent. It has been reported that incidence is 5% in the USA [8], 25% - 38% in Iraq [9] and 43% in the Noruba in Nigeria [10]. Many factors, including gender, age, and ethnicity, may have effect on joint hypermobility. It has been reported that this occurs more frequently in females, particularly those of African and Asian descents, and the hypermobility decreases with age [11] [12]. For example, a survey among 12,853 UK inhabitants shows the prevalence of JHS is 2.5 to 1 for female to male [13]. Among the 12,853 participates, 40% complained that the pain was so severe that it affected their daily life [13]. Despite the high incidence of JHS, the pathology studies on this issue are still very limited [14] [15]. Researchers proposed that JHS is due to the abnormal encoding of connective tissue proteins, such as the abnormal ratio of type III to type I collagen [16] [17]. JHS is defined as one of hereditary connective tissue disorders (HCDTs) [18]. It is the most common HCDT in clinical practice and could be severe [3] [19]. The connective tissues have relatively low stiffness or inherent laxity, which contributed to the hypermobility and symptoms [20].
The objective of the current work is to study the relationship between the soft connective tissue stiffness and the energy loss of the tissue, and investigate the effects of hypermobility on muscle activity experimentally. A differential equation model, Kelvin-Voigt model, was used for the theoretical analysis. Muscle activity about the ankle joints of women with and without joint hypermobility was measured via electromyography (EMG) during simple functional tasks, and the recorded data were used to correlate with the theoretical analysis. It has been found that as the stiffness of the connective tissues decreases, the energy loss of the tissues increases significantly. The EMG results also showed increased co- contraction of antagonistic muscles, which correlates to increased joint loading. While the mechanical properties of tissues in ankle joint were used to illustrate the effect of stiffness, the result would shed light on the pathology analysis of JHS on any synovial joint.
2. Soft Connective Tissue Modeling
2.1. Kelvin-Voigt Model
With the soft connective tissue such as ligaments and tendons being viscoelastic in nature, their behavior is dependent not only on the stress applied but also on time [21]. Therefore, a differential equation model, Kelvin-Voigt model [22], was chosen for the study. This model consists of a spring and a damper arranged in parallel, as shown in Figure 1 and Equation (1).
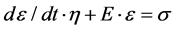 (1)
(1)
In Equation (1), E, the modulus of elasticity, indicates the stiffness of the spring, or in this case the connective tissue stiffness. The damping coefficient η is responsible for the time dependent aspect of the tissue’s viscoelastic behavior.
Figure 1. The Kelvin-Voigt model used for the analysis [23].
Also in the equation, t is time and 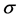 is stress applied. Once the equation is developed, the strain
is stress applied. Once the equation is developed, the strain 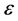 can be solved as shown in Equation (2) using typical differential equation solving procedures.
can be solved as shown in Equation (2) using typical differential equation solving procedures.
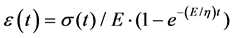 (2)
(2)
2.2. Kelvin-Voigt Model in Modeling of Soft Connective Tissues
Biological tissue properties vary greatly depending on sex, age, and many other factors [21]. As a result, any values chosen for the analysis were not going to be all-encompassing. Meanwhile, because the behavior of the soft connective tissue is not purely linearly elastic, the modulus of elasticity E is not a constant predictable value. In addition, the properties vary with the type of soft connective tissue. While the purpose of the current study is to investigate the effect of the stiffness on the energy loss of various connective tissues, property values for the Achilles tendon’s were used as approximate values in Equation (2).
The median value of stiffness was assumed to be 500 MPa. The damping coefficient η = 200 was chosen initially. Regarding the chosen stress, based on the fact that an Achilles tendon with a cross sectional area of 1 cm2 can bear between 500 kg and1000 kg of mass, a maximum stress of 60 MPa was chosen to be applied to the model [22]. Additionally, the maximum strain that the tissue can take prior to damage is 10%.Since the model being developed was not intended to reproduce rupture but to study the elastic energy lost by the tendon, the maximum strain was chosen to be less than 10%, which would provide for normal tendon operation. Initial strain and stress conditions at t = 0 seconds were assumed to be ε = 0% and σ = 0 MPa. Once the boundary conditions were chosen, a set of linear equations was created to govern the increase and decrease in stress. While realistically stress would likely not increase linearly (due to changing cross sectional area), the stress was approximated as linear for the sake of simplicity. It should be noted that although some assumptions were used to simplify the problem, the trend analysis of the effect of the stiffness on the energy loss should be still valid.
2.3. Results and Discussion on Modeling of Soft Connective Tissues
A MATLAB code for the simulation was developed to study the stress and strain relationships. Stress and strain curves for stiffnesses of 1000 MPa, 500 Pa, and 25 MPa are shown in Figures 2-4, respectively. In each plot, a loading cycle of
Figure 2. Stress and strain curves for stiffness of 25 MPa.
Figure 3. Stress and strain curves yielded for stiffness of 500 MPa.
Figure 4. Stress and strain curves yielded for stiffness of 1000 MPa.
stress was plotted. That is, stress increases from zero and reach a maximum of 60 MPa, then the stress decreases to zero. Because the strain is limited to less than 10%, there is no permanent deformation. When the stress returns to zero, so does the strain. It is clear that the relationship between the stress and strain was not linear, which was expected because the tendon is not purely elastic but has a viscous component as well. The hysteresis loop can be seen very clearly in the plots. Since the area under a curve on a stress-strain diagram yields the toughness (or energy absorbed), the area inside the hysteresis loop yields the energy lost due to tendon viscosity [22]. Integrating both curves and subtracting the area under the lower curve from the area under the upper curve yielded the elastic energy loss. This means that when a load bearing activity is done with the soft connective tissue engaged, the tissue returns a portion of the energy, but also loses a portion imparted.
The relationship between energy loss (percentage) and the modulus of elasticity is shown in Figure 5. In the figure, E changes from 25 MPa to 1000 MPa and an exponential trend line seems to best fit the data in the plot. The trend line equation is shown in Equation (3). It can be seen from the figure that as the modulus of elasticity decreases (which indicates the stiffness of the connective tissue deceases), the energy loss increases significantly. While the mechanical properties of tissues in an ankle joint were used to illustrate the effect of stiffness, the result would shed light on the pathology analysis of JHS on any synovial joint. As aforementioned, for the synovial joints with HJS, the connective tissues have relatively low stiffness or inherent laxity [19]. The relatively higher energy loss of the connective tissue around the joints with HJS might lead to the symptoms such as weakness and pain.
 (3)
(3)
3. Experimental Approach
3.1. Hypermobility and Muscle Function
To correlate with the theoretical model above, an experiment was performed to look at muscle function of the ankle joint during functional tasks. Several factors have been suggested as the cause of chronic ankle instability, including anatomic instability, muscle weakness, and proprioceptive deficits. Those with joint hypermobility syndrome experience joint movements that extend beyond the normal range of motion, a similar symptom to those who have experienced ankle sprains. In many cases of instability, weakness of the peroneal muscle was reported. The peroneus longus muscle is responsible for both eversion and plantar flexion. Other muscles of the ankle responsible for plantar flexion include the gastrocnemius, soleus, plantaris, and the posterior tibialis. The anterior tibialis, extensor hallicus longus, and extensor digitorum longus are the muscles of the ankle responsible for dorsiflexion. Together, these muscles function to
Figure 5. Stress and strain curves yielded for stiffness of 1000 MPa.
stabilize the ankle joint and also enable the motion of the ankle [24].
Hypermobile ankles exhibit a high degree of instability due to the overall laxity of the ankle ligaments. In order for a person with hypermobile ankles to complete the same task as an individual without hypermobile ankles, it is expected to find a larger number of muscles contracted. This increased contraction correlates to an increased load on the ankle [25]. Thus, it is expected that a hypermobile ankle generates a greater contact force due to the necessary increase in muscle recruitment, which might cause the frequent symptoms of pain in JHS. Therefore, the purpose of this experiment is to not only correlate the findings above (that decreased tissue stiffness leads to increased work), but also to investigate the existence of co-contraction in hypermobile ankles, through electromyography (EMG). An electromyogram is a test that records the electrical activity of muscles. When muscles are active, they produce a voltage that is proportional to the level of force generated.
3.2. Experimental Methods
For this study, the ankle function of two subjects was compared: one with hyper- mobility, and one without. EMG electrodes were placed over the tibialis anterior (TA), extensor digitorum longus (EDL), peroneus longus (PL), lateral gastrocnemius (LG) and soleus (SOL) of the left leg (Trigno; Delsys Inc., Natick MA, USA). EMG data were acquired while the subjects performed repetitive heel raises (ankle plantarflexion with eversion) for one minute while seated with a 20 kg weight over their knees. The repetitive motion was paced to reduce timing variability between subjects. Subjects then performed repetitive toe raises (ankle dorsiflexion with inversion) following the same procedures.
The raw EMG data were normalized by maximum voluntary contraction (MVC) and RMS filtered with a 125 ms window in order to better compare the muscle activation amplitudes between subjects. MVC normalization allows amplitudes to be reported in terms of percent maximum contraction for each respective muscle, otherwise signals from different sensors, muscles, and subjects would not be comparable [26].
3.3. Experimental Results and Discussion
The muscles that contribute directly to the motion of the ankle plantarflexion with eversion task are the PL, LG, and SOL. The hypermobile subject showed significantly less LG activation (Figure 6), but similar SOL and PL activations compared to the normal subject. It was expected that the hypermobile subject would use more muscle effort to perform the same task, in order to make up for the loss in energy from the less stiff tendons. It should be noted that the hypermobile subject had significantly stronger leg muscles than the normal subject, which could account for the decrease in LG activity. However, the LG and SOL muscles tend to generally work in unison. Since the SOL activation was not similarly reduced in the hypermobile subject, this muscle may have been compensating for the loss of energy. A larger study with subjects paired by strength
Figure 6. Normalized EMG for lateral gastrocnemius during plantarflexion task.
is warranted to flush out these details, but this preliminary work shows potential evidence of work lost by the abnormal elasticity of the Achilles tendon.
The TA and EDL muscles serve as antagonists during the plantarflexion with eversion task. Increased activity would mean that these muscles are co-con- tracting, which effectively increases the stiffness of the ankle during the motion as well as the forces experienced by the ankle joint. The hypermobile subject showed slightly increased TA activity and significantly higher EDL activity during this task (Figure 7). This result indicates that the hypermobile subject is relying on co-contraction for this task, which could explain the tendency for patients with JHS to experience joint pain and develop osteoarthritis.
The muscles that contribute directly to the motion of the ankle dorsiflexion with inversion task are the TA and EDL. For this task, all muscle activations were similar between subjects, except for the PL, which was significantly higher for the normal subject (Figure 8). These results suggest that this task did not cause problems for the hypermobile subject, and this subject also showed less tendency to stabilize the motion with co-contraction than the normal subject.
To summarize, this preliminary experiment showed potential evidence that certain muscles require more activity to make up for the loss of work when hypermobility is present. The results also showed evidence of co-contraction to stabilize the hypermobile joint during certain functional activities. These results were evident in the plantarflexion with eversion task, but not in the dorsiflexion with inversion task. Further work should be completed with a larger subject population to rule out differences between these two particular subjects. Further investigation should also be made into different functional activities that might elicit more detrimental effects of joint hypermobility.
4. Conclusions
In this paper, the Kelvin-Voigt model has been adopted to study the relationship between energy loss and the stiffness of soft connective tissues in synovial joints. The results showed that as the stiffness of the connective tissue decreases, the energy loss increases. While connective tissues of hypermobile joint have relatively low stiffness, more energy loss of connective tissues was predicted. To correlate with the theoretical analysis, preliminary experiments have been per-
Figure 7. Normalized EMG for extensor digitorum longus during plantarflexion task.
Figure 8. Normalized EMG for plantaris longus during dorsiflexion task.
formed, which showed potential evidence that certain muscles require more activity to make up for the loss of work when hypermobility is present. The results also showed evidence of co-contraction to stabilize the hypermobile joint during certain functional activities. Further work should be completed with a larger subject population with different functional activities.
Cite this paper
Tatarkov, S.A., Tesny, A.C., Lauck, B.M., DiBerardino III, L.A. and Shen, H. (2017) Connective Tissue Energy Loss Comparison between Joints with and without Hypermobility. J. Biomedical Science and Engineering, 10, 18-27. https://doi.org/10.4236/jbise.2017.105B003
References
- 1. Child, A.H. (1986) Joint hypermobility Syndrome: Inherited Disorder ofCollagen Synthesis. Journal of Rheumatology, 13, 239-243.
- 2. Beighton, P., Grahame, R. and Bird, H. A. (1989) Genetic Aspects of the Hypermobility Syndrome. Hypermobility of Joint. 2nd Editon. Berlin: Springer, 55-66. https://doi.org/10.1007/978-1-4471-3900-3_5
- 3. Grahame, R. (2003) Hypermobility and hypermobility syndrome. Hypermobility syndrome - recognition and management for physiotherapists. London: Butterworth-Heinemann, 1-14.https://doi.org/10.1016/B978-0-7506-5390-9.50005-8
- 4. Keer R. (2003) Management of the Hypermobile Adult. Hypermo-bility syndrome-recognition and management for physiotherapists, 87-106. https://doi.org/10.1016/B978-0-7506-5390-9.50011-3
- 5. Grahame R. (1990) The hypermobility syndrome. Annals of Rheumato-logical Diseases, 49,199-200.https://doi.org/10.1136/ard.49.3.199
- 6. Cherpel, A. and Marks, R. (1999) The benign joint hypermo-bility syndrome. New Zealand Journal of Physiotherapy, 27, 9-22.
- 7. Dolan, A., Hart, D., Doyle, D. and Grahame, R. (2003) The Relationship of Joint Hypermobility, Bone Mineral Density and Osteoarthritis in the General Population: the Chingford Study. Journal of Rheumatology, 30, 799-803.
- 8. Jessee, E.F., Owen, D.S. andSagar, K.B. (1980) TheBenign Hypermobility Syndrome. Arthritis Rheumatology, 23, 1053-1056. https://doi.org/10.1002/art.1780230914
- 9. Al-Rawi, Z.S., Al-Aszawi, A.J. and Al-Chalabi, T. (1985) Joint Mobility among University Students in Iraq. British Journal of Rheumatology, 24, 326-331. https://doi.org/10.1093/rheumatology/24.4.326
- 10. Birrell, F.N., Adebajo, A., Hazleman, B.L. and Silman, A.J. (1994) High Preva-lence of Joint Laxity in West Africans. British Journal of Rheumatology, 33, 56-59. https://doi.org/10.1093/rheumatology/33.1.56
- 11. Remvig, L., Jensen, D.V. and Ward, R.C.(2007) Epidemiology of General Joint Hypermobility and Basis for the Proposed Criteria for Benign Joint Hypermobility Syndrome: Review Of The Literature. J. Rheu-matol,34, 804-809.
- 12. Simmonds, J.V. and Keer, R.J.(2007) Hypermobility and the hypermobility syndrome. Man. Ther.12, 298-309.https://doi.org/10.1016/j.math.2007.05.001
- 13. Mulvey, M.R., Macfarlane, G.J., Beasley, M., Symmons, D.P., Lovell, K. and Keeley, P., et al.(2013) Modest Association of Joint Hypermobilitywith Disabling and LimitinGmusculoskeletal Pain: Results from a Large-Scale General Population-BasedSurvey. Arthritis Care Res. (Hoboken), 65, 1325-1333. https://doi.org/10.1002/acr.21979
- 14. Luder, G., Schmid, S., Stettler,M., Mebes, C.M., Stutz, U.,Ziswiler, H. andRadlinger, R. (2015) Stair climbing - An Insight and Comparison between Women with and without Joint Hypermobility: A Descriptive Study.Journal of Electromyography and Kinesiology,25, 161-167.https://doi.org/10.1016/j.jelekin.2014.07.005
- 15. Gazit, Y., Jacob, G. and Grahame, R. (2016) Ehlers - Danlos Syndrome - Hypermobility Type: A Much Neglected Multisystemic Disorder. Rambam Maimonides Med J. 7, e0034, 1-10.
- 16. Grahame, R. (2003) Hypermobility and the Heritable Disorders of Connective Tissue. Hypermobility Syndrome-Recognition and Management For Physiotherapists. 15-26. https://doi.org/10.1016/b978-0-7506-5390-9.50006-x
- 17. Child, A.H. (1986) Joint hypermobility Syndrome: Inherited Disorder of Collagen Synthesis,Journal of Rheumatology, 13, 239-43.
- 18. Zweers, M.C., Hakim, A., Grahame, R. and Schlkwijk, J. (2004) Joint hypermobility Syndromes: the Pathophysiological Role of Tenascin-X Gene Defects,Arthritis and Rheumatism, 50, 2742–2749.https://doi.org/10.1002/art.20488
- 19. Grahame R. (2001) Time to Take Hypermobility Seriously (in adults and children). Rheumatology, 40, 485-487.https://doi.org/10.1093/rheumatology/40.5.485
- 20. Russek, L. (1999) Hypermobility Syndrome,Physical Therapy,79, 591-597. https://doi.org/10.5041/rmmj.10261
- 21. Morales-Orcajo, E., de Bengoa Vallejo, R.B. Iglesias, M.L. and Bayod, J. (2016) Structural and Material Properties of Human Foot Tendons. Clinical Biomechanics,37, 1-6.https://doi.org/10.1016/j.clinbiomech.2016.05.014
- 22. Robi, K., Jakob, N., Matevz, K. and Matjaz V. (2013). The Physiology of Sports Injuries and Repair Processes, Current Issues in Sports and Exercise Medicine, Michael Hamlin, In-Tech.https://doi.org/10.5772/54234
- 23. Özkaya, N., Nordin, M., Goldsheyder, D. and Leger, D. (1999) Fundamentals of Biome-chanics EquilibriumMotion and Deformation. https://doi.org/10.1007/978-1-4757-3067-8
- 24. Lentell, G. L., Katzman, L. L. and Walters, M. R. (1990) The Relationship between Muscle Function and Ankle Stability, Journal of Orthopaedic& Sports Physical Therapy, 11, 605-611.https://doi.org/10.2519/jospt.1990.11.12.605
- 25. Ebig, M., Lephart, S. M., Burdett, R. G., Miller, M. C. and Pincivero, D. M. The Effect of Sudden Inversion Stress on EMG Activilty of the Personeal and Tibialis Anterior Muscles in the Chronically Unstable Ankle.Journal of Orthopaedic& Sports Physical Therapy, 26, 73-77.https://doi.org/10.2519/jospt.1997.26.2.73
- 26. Merletti, R. and Farina, D. (2016) Surface Electromyography. Wiley, Hoboken, New Jersey.https://doi.org/10.1002/9781119082934









