Journal of Applied Mathematics and Physics
Vol.05 No.04(2017), Article ID:75354,7 pages
10.4236/jamp.2017.54067
Whispering Gallery Modes Formed by Scattering of an Electromagnetic Plane Wave by Two Cylinders
Arnold Abramov1, Yutao Yue2*, Chunlin Ji1, Ruopeng Liu1, Xue Li2, Juehui Zhou1, Alexander Kostikov3
1Kuang-Chi Institute of Advanced Technology, Shenzhen, China
2Shenzhen Kuang-Chi Innovative Technology Co. Ltd., Shenzhen, China
3Donbass State Engineering Academy, Kramatorsk, Ukraine




Received: February 7, 2017; Accepted: April 9, 2017; Published: April 12, 2017
ABSTRACT
We report the effect of scattering of electromagnetic plane waves by two cylinders on whispering gallery mode (WGM) formation in a cylinder. WGM can occur because of the presence of additional cylinder scatterers at specific location, while WGMs can only form in a single cylinder for specific cylinder radius and/or wavelength values, the matching accuracy required would be much greater than that required in our model for the additional cylinders locations. Analysis of the general solution to the problem showed that the effect can be explained by the interference of waves scattered by additional cylinders and incident on the main cylinder.
Keywords:
Scattering, Wave, Cylinder, WGM

1. Introduction
The term “whispering gallery modes” (WGMs) was introduced by Lord Rayleigh to explain the effects of sound propagation a circular gallery [1]. The name itself reflects the fact that sound in enclosed spaces can propagate along such concave walls. Laser radiation that is attached to the perimeter of a miniature disk by multiple reflections from concave walls can be treated as an optical analogue of the “whispering gallery”. If the reflection surface is sufficiently smooth, the radiation then propagates with minimal losses. However, because the lateral surface is not smooth and has a nonzero radius of curvature, part of the wave then leaks out. When the radius of curvature increases, more radiation remains inside the disk. WGMs can thus be used to create electromagnetic cavities, as initially noted by R. Richtmyer [2]. This spherical form is the simplest form that can be used in fabrication of a resonator using WGMs. The interaction of spherical particles with electromagnetic waves has been studied theoretically for more than a century, dating back to the work of Mi [3], who considered the scattering of light by spherical particles, and Debye, who studied the scattering of waves on a sphere in the form of a series of refracted and reflected waves of various order [4]. However, despite the fact that this problem (the scattering of waves on an axisymmetric particle) is well known and has been studied for a long time, new and important results were obtained in 2004: the authors of Ref. [5] found and studied a narrow, high-intensity beam of light (called a photonic nanojet) that was generated at the shadow-side surfaces of dielectric cylinders that were illuminated by a plane wave. The renewed interest to cylinder scattering of plane waves led to a detailed study of the conditions required to produce a WGM. V.V. Kotlyar et al. [6] found that the WGM formed a focal spot outside the cylinder, and also determined the contributions of the cylinder eigenmodes to WGM formation. In general, fundaments of WGM propagation and its applications described in Ref. [7]. The effect of multiple cylinders scattering of an electromagnetic plane-wave on the formation of high field intensity areas studied in [8].
2. Modeling and Results
Our model consists of two cylinders. One of these (marked as A on Figure 1) is a basic cylinder, within which we consider WGM formation. The other cylinder (marked B on Figure 1) has an assistive function. The position of cylinder B is varied relative to the basic cylinder with the purpose of finding a location at which the intensity of the WGM increases. Our model, including all distances and notations, is presented in Figure 1. The wave is incident from the left side on the pair of cylinders. The wave propagation direction is along the axis of symmetry of the cylinders, and is selected as the x axis. The origin of coordinates corresponds to the center of main cylinder A. The propagation and scattering of the electromagnetic plane wave was studied using MATLAB toolbox that was developed in Ref. [9]. A transverse-electric (TE) polarized plane wave (λ = 532 nm)
Figure 1. Geometry to simulate scattering of plane wave by two cylinders.
was used as the incident wave. The mesh grid size in the space was equal to 0.04 μm (0.075 of wavelength). The electric permittivity ε = 1.59 (quartz glass), and cylinder’s A radius RA = 4λ. For cylinder B (where the latter is introduced below), the radii RB = 0.25 RA were used. All distances below are measured in μm.
The calculated distribution of the absolute field intensity value is shown on Figure 2(a). As shown, the scattering process leads to the formation of a photonic jet for the single cylinder A. Next we used additional cylinder B. An image for comparison of the single cylinder case with that of our model is shown in Figure 2(b) (Lx = −2.7, Ly = 0.5).


Figure 2.Distribution of the absolute value of total field scattered by one (a) and two (b) dielectric cylinders.
To determine how the positions of cylinder B affect the maximal absolute field value inside the cylinder A, we varied its positions by moving the centers within the ring defined in polar coordinates as interval of radii [RA + RB, RA + 1.6*RB]. Each step in the ring was 0.06 RB/10 along the radius, with an angle step of (p/2)/75. The resulting picture is shown in Figure 3. The positions of cylinder B that were used in Figure 2 correspond with the data used for Figure 3.
3. Formation of WGM Due to Scattering on Neighboring Cylinder
We associate the near-surface area of high field intensity with WGM propagation, because the specific feature of WGMs is that the high intensity field in these modes is concentrated near the cavity walls. The absence of high field intensity areas inside a single scattering cylinder A indicates that WGM is caused by the presence of the additional cylinder B.
In general, the WGM are characterized by the specific value of the following relationship: cylinder radius/wavelength. As an example we consider simple expression 2pRn/l = Tml [10], where Tml is the lth root of the mth order Bessel function. This means that if the wavelength is known, then to determine the propagation of (ml) mode we must choose the cylinder radius based on the expression above. Additionally, when this mode makes a larger contribution to the field intensity, then the radius must be defined more accurately [6] [8]. For example, for a mode with m = 15, when the intensity is increased by eight times, then the accuracy of the matching radius is 10−4 l [8]. It therefore follows from Figure 3 that to attain the same increase in intensity, it is sufficient to determine the location within an accuracy of within a few percent of the wavelength value.
In the case of two or more cylinders, the equation for the derivation the WGM will contain a contribution caused by the presence of satellite cylinder. First of all, this means that now WGM are derived by many parameters (radii of the satellite cylinders, distance between cylinders, their mutual orientation, dielectric permittivity), but not only by a relation R/l, as it was for single cylinder (it is confirmed by comparison of Figure 2(a) and Figure 3. Next, due to the presence of satellite cylinder WGM are formed by the interference of incident waves
Figure 3. Distribution of the maximal value of total field inside cylinder A versus location of cylinder B.
and waves scattered by additional cylinder. The latter also follows from the general formulas describing multiple cylinders scattering. Now we analyze the general solution to the scattering problem on multiple cylinders. Our task in this analysis is reduced to an assessment of the contributions to the field inside cylinder A of the components that are associated with cylinder B. Let’s consider the expression that corresponds to the solutions to Maxwell’s equations for our model, which were given in [11]:
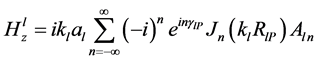 (1)
(1)
where km = 2p/l, al = RA, Jn ? Bessel function of first kind, Rlp ? distance between point P inside lth cylinder and its center, and
 (2)
(2)
The expansion coefficients (ajn, bjn) are related to the single cylinder scattering coefficients (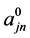 ,
,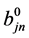 ) and can be obtained by solving the following equation system [11]:
) and can be obtained by solving the following equation system [11]:
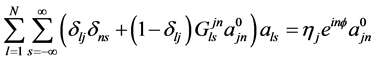 (3)
(3)
where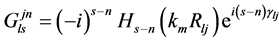 ,
, 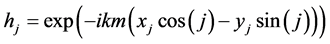 , δ denotes the Kronecker delta.
, δ denotes the Kronecker delta.
Equation (3) allows us to conclude that in the presence of an additional cylinder the amplitude of a certain mode of the first cylinder contains contributions from all modes of the second cylinder. These contributions decrease as the distance between the cylinders increases. Therefore, the resonance is observed only when the location of the second cylinder is close to the edge of the first cylinder.
We now consider why the intensity is maximal in a narrow strip near the edge, but does not decrease gradually if the additional cylinder moves away from the main cylinder. To find a solution, we consider Equation (1) assuming asym- ptotic expressions for the Bessel and Hankel functions for large values of their arguments. Indeed, the arguments are much more than 1 for the parameters of our model (for example: kmal = 2p/l RA = 2p/l*4l = 8p; klRlj < 2p/l*(RA + RB) > 8p). Additionally, in Equation (1), we use only the second term of Equation (2) for Aln, and only the first term in Equation (3) for a1n. From the above, the contribution to the field of the 2-nd cylinder is described as follows:
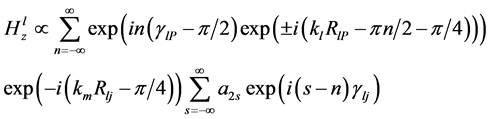 (4)
(4)
Here we have deal with sum of waves with different phases and amplitudes. A well-known gain condition leads to the following equality
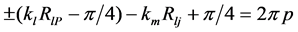 (5)
(5)
where p represents integer numbers. Analysis of this equation for different signs leads to the relationship Rlj − (RA + RB) < λ. This means that the maximum field intensity value occurs if the distance between the centers of the cylinders does not exceed the minimal possible value more than wavelength. Figure 3 confirms the estimates given by Equations (4) and (5).
4. Conclusions
We have simulated the scattering of a plane wave by the pair of cylinders. It was found that WGMs can be formed inside the basic cylinder in the presence of an additional cylinder, without any special requirement for the wavelength or for the radii of the cylinders. However, additional cylinder must be located in specific positions near the edge of main cylinder. The accuracy required for these cylinder locations is much lower than the accuracy required for the setting of the resonant radius of the cylinder at which the WGMs can be observed. Analysis of the general solution to our model has shown that these effects can be explained by the interference of the waves that are scattered by the extra cylinder. Therefore, our work describes a new method for the formation of WGMs in a cylinder.
Acknowledgements
The work was supported by State Key Laboratory of Meta-RF Electromagnetic Modulation Technology (2011DQ782011), Guangdong Key Laboratory of Meta-RF Microwave Radio Frequency (2011A060901010), Composite intelligent materials engineering laboratory, Shenzhen Key Laboratory of Ultrahigh Refractive Structural Material (CXB201105100093A), Shenzhen Key Laboratory of Data Science and Modeling (CXB201109210103A), Shenzhen Science and Technology Plan(JSGG20150917174852555, JCYJ20151015165322766 and JCYJ2015 1015165557141), the introduction of innovative R&D team program of Guangdong Province (NO. 2011D024).
Cite this paper
Abramov, A., Yue, Y.T., Ji, C.L., Liu, R.P., Li, X., Zhou, J.H. and Kostikov, A. (2017) Whispering Gallery Modes Formed by Scattering of an Electromagnetic Plane Wave by Two Cylinders. Journal of Applied Mathematics and Physics, 5, 785-791. https://doi.org/10.4236/jamp.2017.54067
References
- 1. Rayleigh, J.W.S. (1910) The Problem of the Whispering Gallery. Phil. Mag., 20, 1001-1004. https://doi.org/10.1080/14786441008636993
- 2. Richtmyer, R.D. (1939) Dielectric Resonators. J. Appl. Phys., 10, 391-398. https://doi.org/10.1063/1.1707320
- 3. Born, M. and Wolf, E. (1999) Principles of Optics. U. Press, Cambridge. https://doi.org/10.1017/CBO9781139644181
- 4. Debye, E.P. 1908) Das elektromagnetische Feldum einen Zylinder und die Theorie des Regenbogens. Phys. Z., 9, 775-778.
- 5. Chen, Z.A., Taflove, A. and Backman, V. (2004) Photonic Nanojet Enhancement of Backscattering of Light by Nanoparticles: A Potential Novel Visible-Light Ultramicroscopy Technique. Opt. Express, 12, 1214-1220. https://doi.org/10.1364/OPEX.12.001214
- 6. Kotlyar, V.V., Kozlov, D.A. and Kovalev, A.A. (2015) Calculation of the Resonant Radius of a Dielectric Cylinder under Illumination by a Plane TE-Wave. Computer Optics, 39, 163-171. https://doi.org/10.18287/0134-2452-2015-39-2-163-171
- 7. Righini, G.C., Dumeige, Y., F’eron, P., et al. (2011) Whispering Gallery Mode Microresonators: Fundamentals and Applications. Rivista del Nuovo Cimento, 34, 435-488.
- 8. Abramov, A., Ji, C., Liu, R. and Kostikov, A. (2016) Enhancement of the Electromagnetic Waves Intensity by Scattering on Multiple Infinite Cylinders. Journal of Photonic Materials and Technology, 2, 1-5. https://doi.org/10.11648/j.jmpt.20160201.11
- 9. Thierry, B., Antoine, X., Chnitiz, C. and Alzubaidi, H. (2014) µ-Diff: An Open- Source Matlab Toolbox for Computing Multiple Scattering Problems by Disks. arXiv:1409.8186v1 [cs.MS] 29 Sep. 2014.
- 10. Kryzhanovskaya, N.V., Maximov, M.V. and Zhukov, A.E. (2014) Whispering-Gal- lery Mode Microcavity Quantum-Dot Lasers. Quantum Electronics, 44, 189-200. https://doi.org/10.1070/QE2014v044n03ABEH015358
- 11. Schaefer, J., Lee, S.-C. and Kienle, A. (2012) Calculation of the Near Fields for the Scattering of Electromagnetic Waves by Multiple Infinite Cylinders at Perpendicular Incidence. Journal of Quantitative Spectroscopy & Radiative Transfer, 113, 2113- 2123. https://doi.org/10.1016/j.jqsrt.2012.05.019



