Journal of Applied Mathematics and Physics
Vol.05 No.04(2017), Article ID:75352,8 pages
10.4236/jamp.2017.54065
Battery Energy Storage System and Demand Response Based Optimal Virtual Power Plant Operation
Ya-Chin Chang, Rung-Fang Chang
Department of Electrical Engineering, Cheng Shiu University, Taiwan




Received: December 23, 2016; Accepted: April 9, 2017; Published: April 12, 2017
ABSTRACT
With certain controllability of various distribution energy resources (DERs) such as battery energy storage system (BESS), demand response (DR) and distributed generations (DGs), virtual power plant (VPP) can suitably regulate the powers access to the distribution network. In this paper, an optimal VPP operating problem is used to optimize the charging/discharging schedule of each BESS and the DR scheme with the objective to maximize the benefit by regulating the supplied powers over daily 24 hours. The proposed solution method is composed of an iterative dynamic programming optimal BESS schedule approach and a particle swarm optimization based (PSO-based) DR scheme approach. The two approaches are executed alternatively until the minimum electricity cost of the whole day is obtained. The validity of the proposed method was confirmed with the obviously decreased supplied powers in the peak-load hours and the largely reduced electricity cost.
Keywords:
Battery Energy Storage System, Distributed Energy Resource, Demand Response, Iterative Dynamic Programming, Particle Swarm Optimization, Virtual Power Plant

1. Introduction
Under the VPP concept, the integration of DERs enables themselves to be visible to the system operator (SO) and participate in an energy market [1]. In [2], through the advanced information and communication technologies (ICT) of smart grids, the VPP can be operated to compensate the intermittency of DERs’ output irrespective of their locations. The VPP with the controllable loads participating in DR action can optimize the DR scheme by suitably regulating the load powers over the 24 hours to help improve system security for the whole day [3]. In [4], a DR strategy as a load shaping tool is proposed to alleviate the potential new load peaks with minimal infrastructure investments. While in [5], with price uncertainty modeled through robust optimization techniques, a real- time DR model with a linear programming algorithm is used to adjust the hourly load level of a given consumer in response to hourly electricity prices.
Different pilot installations have demonstrated that NaS battery may efficiently be used to stabilize the generation of renewable energy sources as well as to store energy during off-peaks time and dispatch it during peak-loads. The energy capacities of the NaS battery based BESS used in the testing of this study are assumed to be with 80% efficiency and 1/8 energy capacities per hour as the power capacity on each charging/discharging action [6].
In this study, with the functions of the BESS and DR, the optimal VPP operating problem is to maximize the benefit cost (or minimize the electricity cost) of the supplied powers over daily 24 hours. To solve the problem, an iterative dynamic programming optimal BESS schedule approach and a particle swarm optimization based (PSO-based) DR scheme are executed alternatively until the electricity cost minimized. The proposed method is validated on a three feeders’ distribution system.
2. Problem Formulation
With (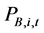 ,
, ) and (
) and (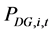 ,
,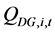 ) respectively representing the scheduled and the generated real and reactive powers by the BESS and the DG at bus i at time t, the real and reactive powers balance equations are shown in (1) and (2) as follows:
) respectively representing the scheduled and the generated real and reactive powers by the BESS and the DG at bus i at time t, the real and reactive powers balance equations are shown in (1) and (2) as follows:
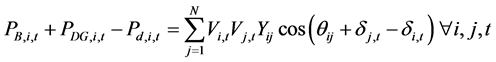 (1)
(1)
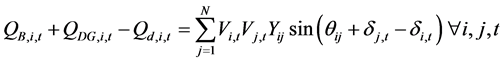 (2)
(2)
The system securities considering the thermal rating of each line i − j and the voltage magnitudes for each node i are shown in (3) and (4) respectively:
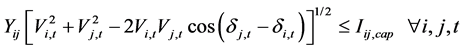 (3)
(3)
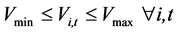 (4)
(4)
where the limits, 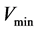 and
and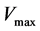 , are 0.95 p.u. and 1.05 p.u. respectively.
, are 0.95 p.u. and 1.05 p.u. respectively.
The total real power access to the main transformers or the grip supply point (GSP) each time t, 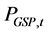 , is limited by
, is limited by
 (5)
(5)
where 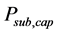 is the capacity of the substation and scaling factor
is the capacity of the substation and scaling factor 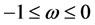 is used to enforce an allowable reverse power from the substation to the grid.
is used to enforce an allowable reverse power from the substation to the grid.
The problem to optimize the DR scheme and BESS schedules is formulated as follows:
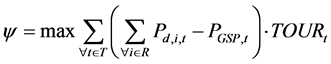 (6)
(6)
s.t. (1)-(5)
Given the TOU rates, TOURt ($/MWh) each time t, the objective 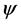 is used to maximize the benefit derived by the difference of the consumer utility cost and the supplied power cost for a whole day. Problem (6) is decoupled into two sub problems to optimize the charging/discharging schedule each BESS and DR scheme respectively, and as the solution algorithm shown in Figure 1 solved by executing an iterative dynamic programming BESS schedule optimization and a PSO-based DR scheme optimization appraochesiteratively until the benefit cannot be increased. The proposed iterative dynamic programming BESS schedule optimization method is introduced in next section.
is used to maximize the benefit derived by the difference of the consumer utility cost and the supplied power cost for a whole day. Problem (6) is decoupled into two sub problems to optimize the charging/discharging schedule each BESS and DR scheme respectively, and as the solution algorithm shown in Figure 1 solved by executing an iterative dynamic programming BESS schedule optimization and a PSO-based DR scheme optimization appraochesiteratively until the benefit cannot be increased. The proposed iterative dynamic programming BESS schedule optimization method is introduced in next section.
3. Iterative Dynamic Programming BESS Schedule Optimization Algorithm
The charging/discharging schedule of each BESS is formulated with the forward dynamic programming (Forward DP) model [7]. The iterative dynamic programming optimal BESS scheduling algorithm is shown in Figure 2 Let state (K, I) indicate the Ith charging/discharging status at Kth interval, and (K − 1, L; K, I) is defined as the transition used to indicate the change of the energy stored in the BESS from status L at interval K − 1 to status I at interval K, namely from states (K − 1, L) to (K, I). At transition (K − 1, L; K, I), the energy stored in BESSi, the power transferred between the BESS and the grid, and the load flow equations to execute are described below:
Figure 1. Iterative dynamic programming optimal BESS scheduling approach.
Figure 2. Three feeders distribution network.
3.1. Charging/Discharging Energy of BESS

where 
states; NT = 24 hours and time interval 


3.2. Charging/Discharging Powers
Case I > L:
Case I < L:
Case I = L:
where 


3.3. Load Flow Equations


where 




3.4. Security Constraints


3.5. Objective Function
At interval K, one of the transitions, 

where 
4. Test Results and Discussions
The distribution system used to validate the proposed optimal VPP operating method is shown in Figure 2, including three feeders to supply power to the commercial, industrial and residential areas respectively with three BESS installations at buses 5, 10 and 16. The total capacity of all main transformers is 60 MVA, the nominal voltage is 22.8 kV, and the current capacity and apparent power rating for each feeder are assumed to be 437 A and 17.26 MVA respectively. The daily base load curves for the three areas, the curves for real system load and the supplied powers are shown in Figure 3. As seen that the system peak-load about 37 MW happens around 14:00 while the system off-peak load about 25 MW appears at about 3:00. The TOU rates ($/MWh) in different time sections are shown in Table 1. The VPP operation is aimed to remove some system demand from the peak-load hours to the off-peak load hours.
Under three power injection capacities, 36 MW, 37 MW and 38 MW, the compositions of three DR schemes based on three regulable percentages, 0%, 10% and 20%, with three energy capacities of each BESS, 20 MWh, 25 MWh and 30 MWh, are tested. Figure 4 shows the benefit obtained from the 9 combinations of three power injection limits with three BESS energy capacities under optimal VPP operating action. As can be found that, among the combinations of 25 MWh with the injection limits, the average benefit $384.3 obtained under the smallest injection limit 36 MW is considered to be the best since the equipment cost with the smallest capacity would be less.
The optimal charging/discharging schedule of each BESS with energy capacity 20 MWh under power injection limit 36 MW are shown in Figure 5. The curves
Table 1. Rates for time of use.
Figure 3. Patterns of load and supplied power curves.
Figure 4. BESS capacities and supply limits vs. obtained benefit costs under optimal VPP operating conditions.
for stored energies of the three BESSs versus the benefit are shown in Figure 6. As can be found that between hours 1 to 8, due to the lower TOU rate, since the stored energy of each BESS continues to increase and the supplied power also increases as well, bigger electricity cost needs to pay for the supplied power, thus the benefit cost is negative. On the other hand, after hour 8, the energy stored in
Figure 5. Optimal BESS charging/discharging schedules.
Figure 6. Stored energy vs. benefit cost.
BESSs begins to discharge therefore the supplied power decreases and accordingly the electricity cost to pay for is lowered and even the benefit cost obtained becomes positive after about hour 18.
5. Conclusion
In this paper, the validity of the proposed optimal VPP operation method is confirmed with the results that the VPP can make the maximum benefit by regulating controllable loads participating in DR contract and charging BESSs in the hours with lower TOU rates and discharging BESSs in the hours with higher TOU rates.
Acknowledgements
This study was sponsored by Ministry of Science and Technology, Taiwan under project number MOST105-2221-E-230-007.
Cite this paper
Chang, Y.-C. and Chang, R.-F. (2017) Battery Energy Storage System and Demand Response Based Optimal Virtual Power Plant Operation. Journal of Applied Mathematics and Physics, 5, 766-773. https://doi.org/10.4236/jamp.2017.54065
References
- 1. Pudjianto, D., Ramsay, C. and Strbac, G. (2008) Microgrids and Virtual Power Plants: Concepts to Support the Integration of Dis-tributed Energy Resources. Proc. of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 222, 731-714. https://doi.org/10.1243/09576509JPE556
- 2. Raab, A.F., et al. (2011) Virtual Power Plant Control Concepts with Electric Vehicles. ISAP, 2011 16th International Conference, 1-6. https://doi.org/10.1109/isap.2011.6082214
- 3. Assessment of Demand Response and Advanced Metering, Federal Energy Regula-tory Commission, Feb. 2011 [Online]. Available: http://www.ferc.gov/legal/staff-reports/2010-dr-report.pdf
- 4. Shao, S., Pipattanasomporn, M. and Rahman, S. (2011) Demand Response as a Load Shaping Tool in an Intelligent Grid with Electric Vehicles. IEEE Trans. Smart Grid, 2, 624-630. https://doi.org/10.1109/TSG.2011.2164583
- 5. Conejo, A.J., Morales, J.M. and Baringo, L. (2011) Real-Time Demand Response Model. IEEE Trans. Smart Grid, 1, 236-242. https://doi.org/10.1109/TSG.2010.2078843
- 6. Tanaka, K., Yoshinaga, J. and Kobayashi, N. (2008) The Sodium-Sulfur Battery for Utility-Scale Applications. Cigre Session, Paris.
- 7. Wood, A.J. and Wollenberg, B.F. (1996) Power Generation, Operation and Control. John Wiley, New York.








