Journal of Applied Mathematics and Physics
Vol.05 No.04(2017), Article ID:75351,7 pages
10.4236/jamp.2017.54064
Sufficient Conditions for Robust Stability of Discrete Large-Scale Interval Systems with Multiple Time Delays
Chien-Hua Lee
Department of Electrical Engineering, Cheng-Shiu University, Taiwan




Received: December 20, 2016; Accepted: April 9, 2017; Published: April 12, 2017
ABSTRACT
The robust stability analysis for discrete large-scale uncertain systems with multiple time delays is addressed in this paper. We establish a method for selecting properly a positive definite matrix Q to derive a very simple upper solution bound of the discrete algebraic Lyapunov equation (DALE). Then, using the Lyapunov equation approach method with this upper bound, several sufficient conditions are presented to guarantee the robust stability of the overall systems. Comparisons between the proposed results with a previous one are also given.
Keywords:
Interval System, Robust Stability, Large-Scale System, Multiple Timedelays, The DALE

1. Introduction
It is known that the system is called an interval system and can be considered as a system with parametric perturbations when matrices of a state equation are interval matrix. In practice, time delay(s) exist(s) in real-life systems and should be integrated into system model. During the past decades, the research of systems with time delay(s) has also become an attractive topic. However, surveying the existing ones, only few works have been devoted to stability analysis and/or stabilization controller design of interval time-delay systems [1] [2] [3] [4] [5]. Besides, compare to single systems, dimensionality of system equations of large- scale systems is higher and hence the control problems of large-scale systems are more complicated. In literature, many contributions have been devoted to the research for these kinds of systems during the past decades [6] [7] [8] [9] [10]. For large-scale interval time-delay system, it is seen that a sufficient criterion has been developed in [5] for the robust stabilization for discrete nonlinear large- scale interval systems with non-integral delays. Of those present works, control problems for systems with both time delays and uncertainties only have been discussed in few works [4] [7] [8]. In this paper, the robust stability testing problem for discrete large-scale interval time-delay systems is discussed. By using the Lyapunov equation approach associated with a very simple upper bound of the solution of the discrete Lyapunov equation, several delay-independent stability criteria are derived for the aforementioned systems. An interesting consequence is that these obtained criteria do not involve any Lyapunov equation. Comparison between the present results and a previous result is also made. It will be shown that the obtained results are better. It is believed that the present schemes are helpful for the controller design of large-scale interval time-delay systems.
2. Main Results
Consider the discrete composite interval time-delay system S which is described as an interconnection of N subsystems 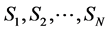 which are represented by
which are represented by
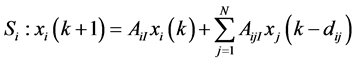 ,
,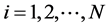 (1)
(1)
where 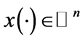 represents the state vector, integer dij > 0 denotes the delay, AijI = AiI for i = j, and AiI and AijI are interval matrices with appropriate dimensions and have the properties:
represents the state vector, integer dij > 0 denotes the delay, AijI = AiI for i = j, and AiI and AijI are interval matrices with appropriate dimensions and have the properties:
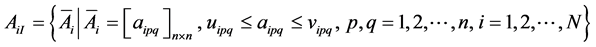 , (2)
, (2)
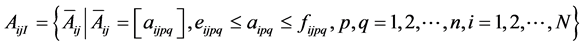 . (3)
. (3)
Define matrices Ui, Vi, Eij, and Fij, respectively, as
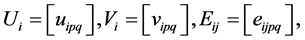 and
and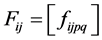 ,
,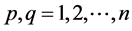 (4)
(4)
In fact, system (1) can also be represented as follows.
 ,
,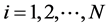 (5)
(5)
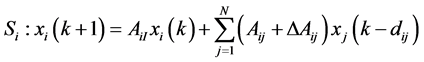 ,
,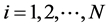 (6)
(6)
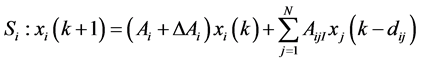 ,
,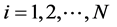 (7)
(7)
where Ai and Aij, respectively, is defined by
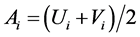 and
and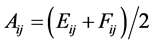 . (8)
. (8)
Here, ΔAi and ΔAij denote the parametric uncertainties with the following properties:
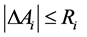 and
and 
where Ri and Sij are defined as


Then, we derive the following criteria.
Theorem 1. For

then the composite uncertain time-delay system (1) or (5) is robustly stable
Proof. The condition (11) infers

which can further implies

Therefore, we obtain 



Here, we choose Qi as

where 
Then, from the Lyapunov Equation (14), we have

Due to the fact that


Then, utilizing these inequalities, we obtain

Substituting this inequality into (16), it is seen that if the condition (12) is satisfied then the right-hand side of (16) is a negative definite matrix. This means that the solution Pi of the Lyapunov Equation (16) has the upper bound
Here, we construct a Lyapunov function as follows.

Taking the forward difference for the Lyapunov function (19) results in


where (15) and the following relation are used.

Therefore, obviously the condition (11) can infer ΔV < 0 and hence the composite uncertain time-delay system (5) is robustly stable. Thus, this completes the proof.
Following the same approach that proposed in the proof of Theorem 1, we have the following results.
Theorem 2. The composite uncertain system (6) or (1) is robustly stable if the following condition is satisfied for

Proof. Using the Lyapunov Equation (7) with

Then, let

It is easy to obtain the stability condition (23). Details of the proof are omitted.
Theorem 3. If the following condition holds for

then the composite uncertain system (7) or (1) is robustly stable.
Proof. From (14), if we choose
and

then the condition (26) can assure the stability of the large-scale system (7) or (1). We also omit the remaining proof.
Remark 1. In [5], a robust stability condition for system model (5) has been driven. We re-write it as follows.

where Ni denotes the number of 






It is obvious that the condition (28) involves an inverse matrix and how to determine the positive constant βi such that (28) is satisfied is an open problem. Furthermore, it is assumed that all eigenvalues of Ai are distinct. The conditions (11), (23), and (26) do not involve any inverse matrix and free variable. It is also not necessary to assume all eigenvalues of Ai are distinct. Therefore, they are less restrictive than (28). Besides, we have found that the tightness of the obtained results cannot be compared.
3. Conclusions
A new approach of the analysis of the robust stability for discrete large-scale interval systems with timedelays has been proposed in this paper. By utilizing the Lyapunov equation approach associated with a simple upper solution bound, several concise criteria have been derived to guarantee the robust stability of the aforementioned systems. The feature of these obtained results is that they do not involve any Lyapunov equation although the Lyapunov approach is utilized. Furthermore, comparing to a previous one, all eigenvalues of the system matrix A are not needed to be distinct in this work and the obtained results do not involve any inverse matrix and free variable. Therefore, they are less restrictive and easy to be checked. It is believed that this work is useful for the stabilization problem of discrete large-scale interval systems with timedelays.
Acknowledgements
The author would like to thank the Ministry of Science and Technology, Taiwan, for financial support of this research under the grant MOST 105-2221-E-230- 003.
Cite this paper
Lee, C.-H. (2017) Sufficient Conditions for Robust Stability of Discrete Large-Scale Interval Systems with Multiple Time Delays. Journal of Applied Mathematics and Physics, 5, 759- 765. https://doi.org/10.4236/jamp.2017.54064
References
- 1. Chang, Y.C., Chen, S.S., Su, S.F. and Lee, T.T. (2004) Simultaneous Static Output-Feedback Stabilization for Discrete-Time Interval Systems with Time-Delay. IEE Proceedings—Control Theory and Applications, 151, 445-452. https://doi.org/10.1049/ip-cta:20040713
- 2. Han, J.F., Tian, H.Z. and Meag, Z.Y. (2010) Criteria for Robust Stability of Dis-crete-Time Dynamic Interval Systems with Multiple Time-Delays. Proceedings of the Ninth International Conference on Machine Learning and Cybernetics, Qingdao, 2010, 890-894.
- 3. Lee, C.H. and Hsien, T.L. (1997) New Sufficient Conditions for the Sta-bility of Continuous and Discrete Time-Delay Interval Systems. J. Franklin Institute, 334B, 233- 240. https://doi.org/10.1016/S0016-0032(96)00074-9
- 4. Stojanovic, S.B. and Debeljkovic, D.L. (2005) The Sufficient Conditions for Stability of Continuous and Discrete Large-Scale Time-Delay Interval Systems. International Conference on Control and Automation, Budapest, Hungary, 2005, 347-352. https://doi.org/10.1109/icca.2005.1528143
- 5. Zhang, X.Z. and Liu, Y.Q. (1998) Stabilizing Decomposition of Interval Nonlinear Interconnected Discrete Control Systems with Nonintegral-delays. Proceedings of the American Control Conference, Philadelphia, Pennsylvania, 1998, 3369-3370.
- 6. Hua, C.C., Wang, Q.G. and Guan, X.P. (2008) Exponential Stabilization Controller Design for Interconnected Time Delay Systems. Automatica, 44, 2600-2606. https://doi.org/10.1016/j.automatica.2008.02.010
- 7. Lee, C.H. and Hsien, T.L. (1997) Delay-Independent Stability Criteria for Discrete Uncertain Large-Scale Systems with Time Delays. Journal of the Franklin Institute, 334B, 155-166. https://doi.org/10.1016/S0016-0032(96)00053-1
- 8. Liu, X. and Zhang, H. (2008) Delay-Dependent Robust Stability of Uncertain Fuzzy Large-Scale Systems with Time-Varying Delays. Automatica, 44, 193-198. https://doi.org/10.1016/j.automatica.2007.05.001
- 9. Park, J.H. (200) Robust Decentralized Stabilization of Uncertain Large-Scale Discrete-Time Systems with Delays. Journal of Optimization Theory and Applications, 113, 105-119. https://doi.org/10.1023/A:1014809314463
- 10. Stankovic, S.S., Stipanovic, D.M. and Siljak, D.D. (2007) Decentralized Dynamic Output Feedback for Robust Stabilization of a Class of Nonlinear Interconnected Systems. Automatica, 43, 861-867. https://doi.org/10.1016/j.automatica.2006.11.010


