Energy and Power Engineering
Vol.09 No.04(2017), Article ID:75340,10 pages
10.4236/epe.2017.94B078
Research on Power Quality Evaluation Based on Radar Chart Method and Fuzzy Membership Degree
Aiqiang Pan1, Jian Zhou1, Peng Zhang1, Ronghui Liu2, Yichao Wang2
1Electric Power Research Institute State Grid Shanghai Municipal Electric Power Company, Shanghai, China
2College of Electrical Engineering, Shanghai University of Electric Power, Shanghai, China




Received: March 10, 2017; Accepted: March 30, 2017; Published: April 6, 2017
ABSTRACT
Aiming at the current limit value of six steady-state energy indexes, the current radar method is used for reference. A method of comprehensive evaluation of power quality based on improved radar method is proposed, which improves the power quality index Type radar pattern to represent the steady-state indicator. Each of the main indicators corresponds to a partial ring, and the angle of the annular portion is mainly affected by the size of the weight. Compared with the previous radar map method to maintain the independence of the indicators and a single indicator of the binding data assessment. The method has the advantages of good feasibility.
Keywords:
Power Quality, Steady-State Index, Sub-Index, Radar Map

1. Introduction
Electricity as a commonly used energy, not only economical and easy to control and conversion. The application of energy has become an important indicator of the level of national development. In recent years, with the continuous development of industrialization and national economic level, the whole society is more and more practical to the power, the power quality requirements are gradually improved, the quality of power quality is directly related to the entire power market economic benefits. With the adjustment of energy structure and the rapid development of national economy, long-distance DC transmission and large power grid interconnection to the fundamental changes in the structure of the grid, the resulting AC and DC hybrid operation of the power system and the increasingly variable power grid negative characteristics , As well as the non-li- near load and time-varying load in the power grid, brought about such problems as harmonics, voltage fluctuation and flicker, three-phase imbalance [1] [2], which deteriorated the power quality index of the grid. Therefore, it is important to develop a suitable power quality assessment method to evaluate the power quality index synthetically and to improve the power quality to optimize the electricity market.
China has proposed nine national standards for power quality to analyze the power quality problem, which is divided into six steady-state indicators and three transient indicators, because the transient index is not clear data limits are not easy to assess, so the current power quality, the comprehensive evaluation mainly starts from the steady state index. This paper combines the contents of national standard of power quality in China [3] [4] [5] [6], and selects 6 of them as steady-state power quality indicators, which are the allowable deviation of supply voltage, voltage fluctuation, voltage flicker, harmonic distortion rate, three-phase voltage Balance, power system frequency tolerance.
The existing methods of comprehensive evaluation of power quality mainly include three categories [7] [8] [9] based on fuzzy mathematics theory, probability statistics theory and intelligent algorithm. These methods solve the problem of comprehensive evaluation to a certain extent, but the traditional mathematical algorithm is The evaluation of power quality indicators can only stay in the written text, and the radar chart method as the representative of the graphics analysis can be more clearly to show the specific indicators of the specific situation, this paper refers to the radar map in the assessment of indicators Simple and clear, clear the characteristics of the combination of fuzzy membership function to carry out the power quality indicators, so that it can more objectively show the advantages and disadvantages of the indicators.
2. Indicator Normalization and Selection
The primary objective of the evaluation of the power quality indicators is to select the appropriate indicators. First, the indicators should be normalized.
(1) Frequency deviation
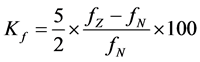 (1)
(1)
fz is the real-time frequency value, fN is the rated frequency value, Kf is the normal value of the frequency deviation.
(2) Voltage deviation
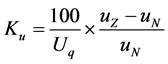 (2)
(2)
uz is the real-time voltage value, uN is the rated voltage value, Uq is the voltage deviation GB allowable limit, Ku is the voltage deviation normalized value.
(3) Voltage fluctuation and flicker
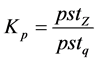 (3)
(3)
Pstz is the real-time flicker value, pstq is the voltage flicker GB allowable limit, Kp is the flicker deviation normalized value.
(4) Harmonic distortion rate
 (4)
(4)
A is the real-time harmonic value, KA is the harmonic distortion rate normalized value.
(5) Odd harmonic voltage content
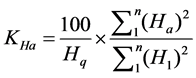 (5)
(5)
Ha is the first harmonic value, H1 is the fundamental harmonic value, Hq is the odd harmonics national standard allowable limit, KHa is the frequency deviation normalization value.
(6) Voltage three-phase imbalance
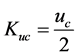 (6)
(6)
uc is the voltage three-phase component, Kuc is the voltage three-phase imbalance normalized value.
After normalization, the indicators are kept at the same level, roughly 1 as the limit, the closer to 0 indicators of the better performance. Excellent indicators in the evaluation of power quality indicators cannot play a corresponding role, and will require the need for composite single index number too much, causing interference to the calculation, should be excluded. Such as odd harmonic voltage from the third harmonic to twenty-fifth harmonic, a total of more than a dozen indicators, if all are evaluated, the index is too large and meaningless, so from the odd harmonic, And for the rest of the indicators, the normalized indicator with a target value less than 0.1 should be excluded and the remaining indicators should be retained.
It should be noted that short-term flicker indicators should not be part of a comprehensive indicator. As shown in Figure 2, short-term flicker assessment results in the vast majority of time is quite good, but the occasional jump, which is different from the other indicators of change, if and other indicators together, it will affect the comprehensive Index value, but also cannot observe the original indicators appear in the transition time period.
3. Empowerment Algorithm
After selecting the appropriate metric, you should calculate the weight. In this paper, subjective analytic hierarchy process and objective entropy weight method combined with the subjective and objective complex weights.
Analytic Hierarchy Process (AHP) as a way to determine the subjective weight, divided into four steps: the establishment of the hierarchical hierarchical structure of the problem, determine the comparison matrix, the calculation of weight [10].
Hierarchical hierarchical structures can usually be divided into target layer, criterion layer and scheme layer.
The comparison judgment matrix represents the comparison of the relative importance between the present level and its associated units for the previous hierarchy, and the scale of the importance is shown in the following Table 1 and Table 2.
Each column of the judgment matrix is normalized:
 (7)
(7)
The normalized judgment matrix is added in rows:
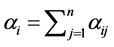 (8)
(8)
Make Ai normalized, seeking weight:
 (9)
(9)
Let the weight values be sorted by weight vectors:
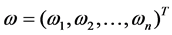 (10)
(10)
Entropy method is a kind of typical objective weighting method. Many objects can be evaluated by multiple indexes. According to the weight obtained by entropy method, a certain value is often large (more than 0.3, sometimes even up to 0.6 phenomenon, which is seriously inconsistent with the importance of indicators. Although the importance of the indicators are not the same, but there should not be a large indicator of the weight of the situation, or by this indicator can reflect the pros and cons of the object , Without regard to other indicators
Table 1. Matrix element scale table.
Table 2. Judgment matrix.
of the patent for the traditional entropy method to improve the objective weight calculation. The first is to establish the model, with m evaluation objects recorded as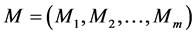 , Suppose there are n evaluation indicators recorded as
, Suppose there are n evaluation indicators recorded as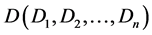 , The value of the evaluation object Mi to the index Dj is recorded as
, The value of the evaluation object Mi to the index Dj is recorded as , The initial information matrix can be obtained:
, The initial information matrix can be obtained:
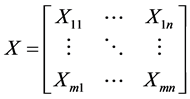
where Xij is the value of the i-th evaluated object under the jth index. The original matrix is dimensionless:
 (11)
(11)
In the case of the jth index, the proportion of the i-th evaluation object is pij:
 (12)
(12)
Calculate the entropy ej of the jth index:

It should be noted that the greater the difference in the index value of each item to be evaluated, indicating that the greater the amount of information reflected by the indicator, the smaller the entropy. While the entropy is too large, indicating that the information provided by the indicator is very small, you can give it appropriate to remove it.
The difference coefficient hj of the jth index is:

Calculate the entropy weight 

The traditional entropy method is used as the objective weight directly after calculating the entropy weight according to the above process, but the modified entropy method needs to correct the entropy. Let the maximum entropy weight obtained by the above formula be




The entropy weight of each index is obtained
If there is a modified entropy weight 


After obtaining the subjective and objective weight value, it will be merged into subjective and objective compound weight:

4. Improved Radar Map Method
Radar graph method due to the different order of the indicators caused by the evaluation results are not unique, the fundamental reason is that when drawing the radar map, the order of linear connection points on the axis of the formation of polygons [11] [12]. When constructing the evaluation function, the polygon area and the circumference are not equal due to the different indexes, and the evaluation results are inconsistent. Therefore, this paper uses the arc instead of the triangular area, and constructs the evaluation function according to the drawn radar map. Transform the composite weights obtained above into the weight angles of the improved radar graphs
The center of the circle as a starting point, the horizontal right to make a ray as the first indicator of the reference axis, in which to take p1 length, with n indicators, then 
Can be calculated fan area is

The normalized value of the composite index can be regarded as normalizing the sector area
Figure 1. Example of six indicators radar.


After the normalized weight of the comprehensive index is determined, the fuzzy evaluation method is used to classify the obtained index.
It is very important to use fuzzy mathematics to deal with the problem of power quality evaluation and the selection and establishment of fuzzy model. The validity of the membership function directly affects the credibility of the final judgment [13]. The quality evaluation can be described by the five-level fuzzy evaluation set V {excellent, good, medium, qualified, unqualified}, and the evaluation criteria of the comprehensive index are shown in Table 3.
The establishment of a single factor evaluation matrix for each sub-index of power quality is the most critical step in evaluating the quality of power. In order to establish the univariate evaluation method of the index to be evaluated, the membership degree of the subordinate index of a specific power quality should be determined on the basis of establishing the membership function density function. Since the index is ambiguous relative to the two quality levels, the membership function between the two levels can be quantified for the five quality levels of the division, where Z1 and Z2 are determined by the actual The situation is determined, X is the index limit.
The index corresponds to the membership function for the excellent quality level

In this function:

Indicators correspond to the membership function of good, medium and qualified quality

Table 3. Comprehensive index rating table.
In this function: the value of parameter K is determined by the national standard limit, preferably
The index corresponds to the membership function for the unqualified quality level

In this function: n = 4.
The above model can be used to describe the relationship between the two quality levels, rather than the membership of the overall qualified range, by describing the membership of the individual quality evaluation index relative to each quality level.
5. Case Study
In this paper, three substations in Shanghai are selected to analyze the energy quality indexes of 2014, and the evaluation indexes and corresponding statistical data are shown in Table 4.
Through the consistency test, we can draw a reasonable index weight. In this paper, we select the priority judgment, frequency deviation > odd harmonics > harmonic distortion> voltage deviation> imbalance in the evaluation of power quality in [14]. The subjective weight is calculated by analytic hierarchy process and then entropy The objective weight of the three sites is obtained, and the weight of the subjective and objective weights of the three sites is obtained. Taking S1 as an example, the weight values of each index are = (0.17, 0.14, 0.17, 0.19, 0.22), They represent the odd harmonic voltage content, imbalance, frequency deviation, harmonic distortion rate, voltage deviation, S1 site drawing radar shown in Figure 2.
After the radar map processing of the composite index into the membership function, the resulting three site membership values were:
S1 (0.211, 0.462, 0.156, 0.098, 0.046)
S2 (0.018, 0.145, 0.236, 0.347, 0.514)
S3 (0.425, 0.301, 0.157, 0.115, 0.023)
According to the principle of maximum membership degree, the fuzzy evaluation results of three sites are as follows: S1 is good, S2 is passed and S3 is excellent. The results of this method are shown in Table 5.
Table 4. Sample data sets to be evaluated.
Figure 2. S1 site measurement data from the radar map.
Table 5. Comparison of the results of the comprehensive evaluation of power quality.
It can be seen from Table 5 that the method is in good agreement with the results of other evaluation methods. It can be seen from Table 4 that the harmonic distortion rate of the substation S2 is excessive, so the power quality should be unqualified, and only the gray correlation method is correctly evaluated with the method, It can be seen that by selecting a reasonable classification interval, this method can effectively classify the power quality and prove the effectiveness of the method.
6. Conclusion
In this paper, the entropy weight method is used to effectively restrict the excessive weight. Appropriate indicators are selected by means of the normalization of individual indicators to ensure the accuracy of the assessment results. Combined with the radar method to deal with the comprehensive index, and then fuzzy evaluation method for classification, effectively combined with the advantages of the two methods, by comparing the results of the traditional algorithms to prove that the evaluation of this method has been greatly improved, The assessment method is reasonable and feasible.
Acknowledgements
The work was supported by Science Project of State Grid Corporation of China (520940150010).
Cite this paper
Pan, A.Q., Zhou, J., Zhang, P., Liu, R.H. and Wang, Y.C. (2017) Research on Power Quality Evaluation Based on Radar Chart Method and Fuzzy Membership Degree. Energy and Power Engineering, 9, 725-734. https://doi.org/10.4236/epe.2017.94B078
References
- 1. Salarvand, A., Mirzaeian, B. and Moallem, M. (2010) Obtaining a Quantitative Index for Power Quality Evaluation in Competitive Electricity Market. IET Generation, Transmission and Distribution, 4, 10-823. https://doi.org/10.1049/iet-gtd.2009.0479
- 2. Mamo, X. and Javerzac, J. (2001) Power Quality Indicators. 2001 IEEE Porto Power Tech Proceedings, 1-4.
- 3. GB/T 12325-2008. Powerquality -Deviation of Supply Voltage.
- 4. GB/T 15945-2008. Power Quality -Frequency Deviation for Power System.
- 5. GB/T 15543-2008. Powerquality -Three Phase Voltage Unbalance.
- 6. GB/T 14549-1993.Qualityof Electrical Energy Supply -Harmoninc in Public Supply Network.
- 7. Farghal, S.A., Kandil, M.S. and Elmitwally, A. (2002) Quantifying Electric Power Quality via Fuzzy Modeling and Analytic Hierarchy. IEE Proceedings: Generation, Transmission and Distribution, 149, 44-49. https://doi.org/10.1049/ip-gtd:20020006
- 8. Li, L.J., Yao, J.G., Long, L.B., et al. (2007) Application of Combination Weighing Method in Fuzzy Synthetic Evaluation of Power Quality. (2007) Automation of Electric Power Systems, 31, 56-60.
- 9. Zhang, M., Lin, T., Cao, J., et al. (2008) A Comparative Study on two Methods for Synthetic Evaluation of Power Quality. Automation of Electric Power Systems, 32, 37-41.
- 10. Yang, J.H., Ouyang, S., Shi, Y.L., et al. (2014) Combined Membership Function and Its Application on Fuzzy Evaluation of Power Quality. Advanced Technology of Electrical Engineering and Energy, 33, 63-69.
- 11. Wang, Y.Y. (2007) The Existing Problems and Improved Measures in Synthetic Evaluation Using Radar Chart. Statistical Education, 14, 18-20.
- 12. Li, G.D., Li, G.Y., Yang, X.D., et al. (2010) A Comprehensive Power Quality Evaluation Model Based on Radar Chart Method. Automation of Electric Power Systems.
- 13. Liu, H.L., Liu, A.X., Zhang, B., et al. (2008) A Fuzzy Comprehensive Evaluation Method of Maintenance Quality Based on Improved Radar Chart. ISECS International Colloquium on Computing, Com-munication, Control and Management, 638-642.
- 14. Li, Y.J. and Wang, Y.L. (2012) Application of Improved Radar Chart in Compressive Evaluation of Power Transmission and Transformation Project. North China Electric Power University, Beijing.






