Energy and Power Engineering
Vol.09 No.04(2017), Article ID:75338,10 pages
10.4236/epe.2017.94B076
A Novel Method of Auxiliary Power Supply Used in Wide-Range High Voltage Input DC-DC Converter
Jie Zhang, Liangjie Li, Cuicui Liu
Hubei Collaborative Innovation Center for High-Efficiency Utilization of Solar Energy, Hubei University of Technology, Wuhan, China




Received: March 15, 2017; Accepted: March 30, 2017; Published: April 6, 2017
ABSTRACT
In high voltage input DC-DC converter, auxiliary winding of isolation transformer is usually used to supply power for control circuit. Due to the wide- range of input voltage, the variable output voltage of auxiliary winding will cause a series of problems, such as variable drive pulse amplitude, increased driver switching devices loss and drive transformer core saturation. This paper analyzes the influence of variable output voltage of auxiliary winding in detail. A novel method is proposed to solve the problem of large variation range of auxiliary winding output voltage, which is adding a buck converter between the auxiliary winding and the control circuit. A dual switch forward convert has been designed with 300 V - 800 V input and 24 V/5 A output. The results show that this method is effective by comparing the different results of using buck converter or not.
Keywords:
Dual Switch Forward Converter, Wide-Range Input, Auxiliary Winding of Power Supply, Buck Converter

1. Introduction
Among various kinds of inverters, due to the different output voltage, the dc voltage changes in a relatively wide range. Double transistor forward DC/DC converter with its good isolation performance, resistance of straight bridge arm, low switch stress of power components is widely used for high input voltage. Therefore, in all kinds of inverters, double transistor forward converter is the common solution for auxiliary power of inverter.
Double transistor forward converter with high and wide range input voltage is widely researched home and abroad. In literature [1], the duty ratio of a novel resonant reset asymmetrical dual-switch forward converter is increased to more than 50%.
However, the rang of input voltage is very narrow. Literature [2] use two-level DC/DC converter for the solution to solve the problems for wide range input voltage in special military vehicle system. That double transistor forward circuit and double Buck Boost circuit cascade is only applicable from 85 V to 450 V, and the drive control is complex. In literature [3], the double transistor forward auxiliary power with high and wide range input voltage whose equivalent circuit model of drive is established because of the characteristics of no external power supply, high frequency and high voltage isolation, and low latency. Literature [4] uses driver chip with time-sharing self power supply technology to drive the bridge arm, which can simplify the drive circuit, and solve the feedback problem of two-transistor Fly back circuit, develop an auxiliary power supply prototype whose input voltage ranges of 80 V to 800 V, and 24 V output voltage. Literature [5] designs an auxiliary power whose starting branch can be automatically disconnected after working, input voltage ranges between 300 V and 2500 V, and 24V output voltage. Above literature research two-Transistor Forward converter with high and wide range input voltage in the operation mode, connection mode, drive circuit, feedback and starting circuit respectively, but haven't found the effect of auxiliary winding. Therefore, in order to guarantee the stability of the power supply, researching the power supply of two-Transistor Forward converter with high and wide range input voltage is of great significance.
Double transistor forward and Flyback converter with high and wide range input voltage have the problem of unstable power supply of auxiliary winding. Unstable power supply will cause the design of the power supply of control chip, the drive circuit, the isolation transformer harder, has a great influence on the efficiency and temperature rise of converter. Stable power supply way is the key to guarantee the normal operation of double transistor forward converter with high and wide range input voltage.
2. Power Supply Way of Auxiliary Winding for Two-Transistor forward Converter
In this paper, the principle of double transistor forward converter based on peak current-model control mode is presented.
UC3845 is selected as controller, a double transistor forward converter is developed whose input voltage ranges between 300 V and 800 V, 24 V output voltage and 5 A output current.
2.1. Power Supply of Chip Starting
The startup current of UC3845 is 2 mA, which is supplied by the DC bus voltage through partial pressure resistance. The resistance is 100 kΩ. The startup current is between 2.85 mA and 7.86 mA.
The design of Power supply circuit for chip starting is shown in Figure 1.
Figure 1. Power supply circuit of chip starting.
Equation is the startup current calculated formula of UC3845:
 (1)
(1)
When the power supply in the minimum input voltage Vin-min = 300 V, the resistances R12 and R13 is in parallel, which is cascaded with R14, then VCC = 8.5 V. When Vin > 675 V, the zener diode starts work, so VCC = 18 V.
2.2. The Power Supply of Auxiliary Winding
If the control circuit was supplied only by the starting circuit, the power supply capacity is serious short. By reducing current limiting resistor to improve the power supply capacity, it is equivalent to a linear power supply, which will cause huge loss of power supply circuit. To reduce power loss and improve the efficiency of power supply, the control circuit is supplied through integrating a fly back transformer auxiliary winding.
2.3. Design of Drive Circuit
Double tube driver needs two isolation drive pulse. Transformer has strong drive, simple structure, strong reliability, strong anti-jamming capability, and good insulation effect. This paper adopts transformer isolation drive mode. Drive circuit selects the topology of three windings demagnetization and the two lines of output. The deliverypoint is the input of isolation transformer. The drive circuit is shown in Figure 2.
3. Analysis of Power Supply Problem of Traditional Auxiliary Winding
3.1. Calculation of Supply Voltage for Traditional Auxiliary Power Supply
Auxiliary winding adopts flyback power supply method, and winding port voltage depends on the voltage transformer primary side and the control chip work duty cycle.
Equation (2) is flyback converter ratios calculated formula:
Figure 2. Drive circuit.
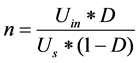 (2)
(2)
Among them: Uin as the input voltage; Us for winding voltage; D for duty cycle.
In order to ensure that the VCC meet the requirements of power supply at any time, we take Uin-min = 300 V, US = 8.5 V, Dmax = 0.5 to the Formula (2).
N = 35.2.
When Uin-max = 800 V, the maximum voltage of the auxiliary winding is Usmax.
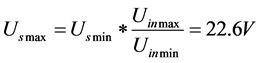
The secondary winding of the power supply voltage range is 8.5 V - 22.6 V.
3.2. Analysis of Traditional Auxiliary Power Supply
Power supply instability has three effects on circuit design.
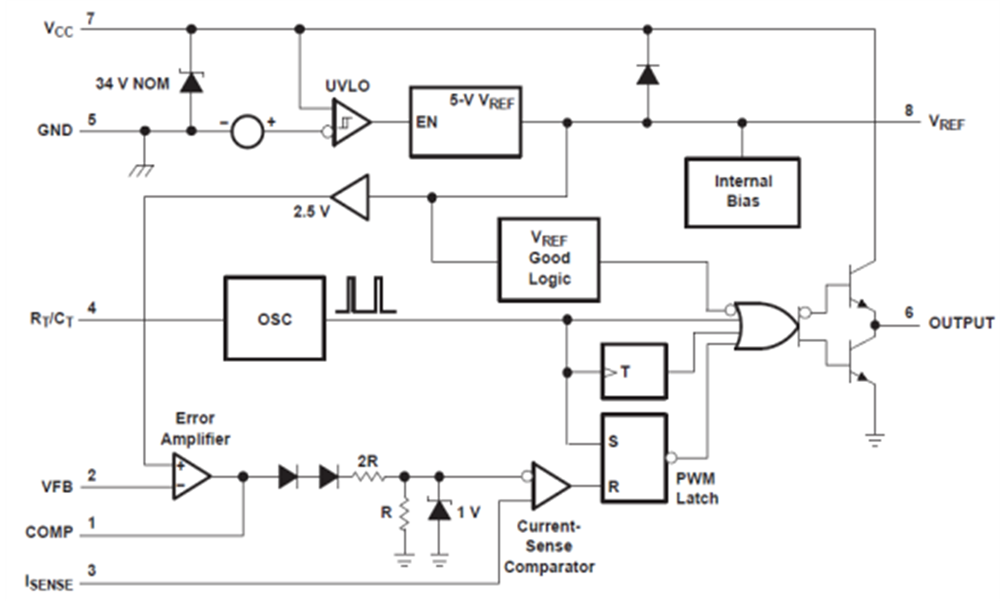
3.2.1. The Impact on the Trigger Pulse Amplitude
UC3845 control chip output is a push-pull circuit structure and its internal structure is shown in Figure 3. The OUTPUT pulse voltage is decided by the supply port VCC. When the trigger pulse is low, OUTPUT port is connected to ground, VDS = 1 V, then OUTPUT port voltage is 1 V. When the trigger pulse is high, the power supply port voltage VCC drop VDS, then output.
3.2.2. The Impact on Isolation Transformer
Isolation transformer is a fixed ratio, and the main circuit switch is selected SCT240KEC that gate and drain voltage VGSS is limited between-6 V and 22 V and the threshold voltage is limited between 1.6 V and 4 V. Transformer variable ratio selected 1: 1: 1: 1. Isolation transformer core is EE25, which material is ferrite PC40. Taking the natural cooling mode into account, magnetic flux swing
Figure 3. UC3845 internal structure.
amplitude ΔB take 0.2 T, and isolation transformer inductance LP value is 1.5 mT.
Equation (3) is the relationship between the input voltage of the forward converter and the swing of the flux density calculated formula:
 (3)
(3)
Among them: Ui-transformer primary voltage (V); N1-the primary turns of the transformer; Ae-core effective cross-sectional area (m2); ΔB-magnetic flux density swing (T); Ton-conduction time (s).
When transformer design is completed, N1 and Ae is a fixed value, Ton is controlled by a control chip, which will not affect the magnetic flux density swing in the drive circuit. So the transformer is directly proportional to the input voltage VCC and ΔB. if the VCC changes from 8.5 V to 22.6 V, the maximum magnetic flux density swing range is 0.2 T to 0.53 T, which will exceed the saturation magnetic flux density of the ferrite core material 0.5. The experimental phenomenon is that with the VCC rise, resulting in transformer copper consumption increases, the transformer temperature rising will be correspondingly increased, resulting in magnetic flux density saturation point down. When VCC voltage is up to 18 V, current is nonlinear growth, rising sharply, transformer saturation, and winding voltage waveform distortion with much higher harmonic components that can make higher maximum potential. Temperature rising sharply rise will damage the transformer and switch tube.
3.2.3. The Impact on the Driver Switch Tube
According to the design requirements, it selects the switching drive for the IRF530N. VGSS is limited between-20 V and 20 V. Gate-to-Source voltage is 2 V - 4 V, and on-resistance is 0.6 Ω. Gate drive circuit is designed to use a 15 V zener diode IN4746. When VCC is greater than 16 V, Zener diode began to work, so the UC3845 pulse amplitude is 15V, resulting in huge loss of drive circuit.
Equation (4) is peak driving circuit current and input voltage calculated formula:
 (4)
(4)
Among them:P0 is driving power (2 W),  is a converter conversion efficiency (0.85), Dmax is maximum duty cycle (0.5), VS is the isolation transformer input voltage.
is a converter conversion efficiency (0.85), Dmax is maximum duty cycle (0.5), VS is the isolation transformer input voltage.
Equation (5) is the effective value of the current calculated formula:
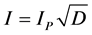 (5)
(5)
When VS changes from 8.5 V to 22.6 V, the variation range of IP is 69.4 mA - 208 mA.
Equation (6) is the conduction loss of the switch tube calculated formula:
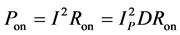 (6)
(6)
When IP changes in 69.4 mA - 208 mA, the highest current conduction loss is 7.1 times of the minimum power consumption.
4. The Solution of the Auxiliary Winding Power Supply
4.1. The Way to Solve the Problem of Traditional Power Auxiliary Winding
By the analysis of the problems existing in the traditional auxiliary winding shows that wide range input voltage can produce very big fluctuation voltage range on the auxiliary winding port. Auxiliary winding power supply instability is the source of the pulse voltage amplitude changes, drive switch damage and isolation transformer saturation. Therefore, the auxiliary winding power supply using a stable supply voltage scheme is the key to solve the problem. There are three ways to provide voltage regulator: zenerdiode,linear power supply,switching power supply.
Zenerdiode: the maximum regulated current of the zener diode is only ten to several tens of milliamps, and the low power regulator is usually about a few hundred milliwatts to several watts .That is not adapted to the need for a larger current.
Linear power supply: the adjust tube work in the linear amplification area, so the load when circuit the current is large. The adjust the collector loss is quite large, power consumption and efficiency is relatively low.
Switching power supply: the adjust tube work in saturated conduction and cut-off state, so it has low power consumption, high efficiency, small size, light weight, and wide voltage range.
Taking the volume and efficiency into consideration, the choice of switching power supply the method. Auxiliary winding voltage range 8.5 V to 22.6 V, and control chip of operating voltage is 8.2 V. Buck converter regulator can achieve auxiliary winding power supply voltage stability
4.2. The Auxiliary Winding Stable Power Supply Program
To solve the wide range input control part of the power supply voltage instability problems, this paper presents a scheme to supply the buck circuit to the auxiliary winding power supply. Wide range of high-voltage input double transistor forward converter auxiliary winding power supply is shown in Figure 4.
The imr16006 integrated control chip control buck circuit is shown in Figure 5. When the buck circuit applied to auxiliary winding,winding voltage convert the VCC port voltage to 9 V/2 W. Not only can it eliminate the drive switch gate drive overpass voltage problem, but also prevent the drive transformer core from saturation and temperature rising. Buck circuit integrated module size is: length + width + height < 30 mm.
5. Experiment and Result Analysis
This experiment have achieved a double transistor forward converter that input voltage is 300 V to 800 V, and output voltage is 24V/5A. The traditional winding
Figure 4. Auxiliary winding power supply diagram.
Figure 5. Buck circuit schematic diagram.
power supply and the program’s experimental waveform were recorded on. When the input voltage is 305 V, 360 V, 601 V respectively, the traditional winding power supply VCC waveform are as shown in Figures 6-8.
The input voltage Vin corresponds to the size of the auxiliary winding supply port VCC, switching drive temperature rising T1 (˚C) and isolation transformer temperature rising T2 (˚C) is shown in Table 1. The room temperature is 20˚C.
From the experimental waveform and recorded temperature rising results show that: with the input voltage increases, the auxiliary winding to provide the supply voltage VCC is increase, and temperature rising of drive switch and isolation transformer are also rise. When the voltage reaches 650 V, the core of the isolation transformer is saturated and the current grows nonlinearly, and the temperature rising exceeds 80˚C within 10 s.
When the buck circuit is applied to the auxiliary winding, the experimental waveform about the power supply VCC are shown in Figures 9-11.
The figure shows: buck circuit does not work, when the power supply port below 9 V. If the power supply port is higher than 9V, the buck circuit make the power supply stabilize at 9 V, so the drive switch and isolation transformer temperature rising is basically unchanged at 30˚C.
Figure 6. Vin and VCC voltage waveform at 305 V.
Figure 7. Vin and VCC voltage waveform at 360 V.
Figure 8. Vin and VCC voltage waveform at 601 V.
Figure 9. Vin and VCC voltage waveform at 305 V.
Figure 10. Vin and VCC voltage waveform at 360 V.
Table 1. The result of experiment.
Note: “-” in Table 1 indicates that the temperature rising exceeds 80˚C.
Figure 11. Vin and VCC voltage waveform at 601 V.
6. Conclusion
In this paper, a wide range input voltage of the double transistor forward power supply using auxiliary winding power supply, the traditional auxiliary power supply problems are analyzed and improved. If there is a buck circuit in the auxiliary winding, it can achieve auxiliary winding power supply voltage stability; this scheme can avoid the selection of the main power switch limited by the gate drive voltage threshold, the saturation of the isolation transformer, and improve the stability of the drive circuit, which is suitable for wide-range input of low power DC-DC converter.
Cite this paper
Zhang, J., Li, L.J. and Liu, C.C. (2017) A Novel Method of Auxiliary Power Supply Used in Wide- Range High Voltage Input DC-DC Converter. Energy and Power Engineering, 9, 703-712. https://doi.org/10.4236/epe.2017.94B076
References
- 1. Gu, X.M. (2005) Study on a Wide Range Dual-Forward Forward DC / DC Converter. Journal of China Electromechanical Engi-neering, 25, 44-48.
- 2. Yu, P.(2011)Study on Wide Range Input Two-Stage DC / DC converter. Chongqing University.
- 3. Hu, L.D., Zhao, Z.H., Sun, C., et al. (2015) Study on Driving of High-Voltage Input Double-Tube Flyback Assisted Power Supply. Journal of Electrotechnical Society,30,161-170. https://doi.org/10.1149/2.0451504jes
- 4. Chen, D.P., Sun, C., Ai, S., etc. (2014) A Wide Range of Dual-Tube Flyback DC / DC Auxiliary Power Supply Design. Power Technology, 11, 2125-2129.
- 5. Hu, L., Sun, C., Zhao, Z.H., et al. (2015) Design of DC-DC Auxiliary Power Supply with High Voltage and Wide Range Input Low Voltage Output. Journal of Electrical Engineering, 2, 103-114.