Energy and Power Engineering
Vol.09 No.04(2017), Article ID:75313,12 pages
10.4236/epe.2017.94B056
Practical Dynamic Security Region Based on Phase Trajectory
Yi Gao1, Jiangtao Chang2, Chao Qin2, Yuan Zeng2, Yingying Liu1, Shengwei Li1
1State Grid Tianjin Power Economics & Technology Research Institute, Tianjin, China
2Key Laboratory of Smart Grid of Ministry of Education, Tianjin University, Tianjin, China




Received: December 7, 2017; Accepted: March 30, 2017; Published: April 6, 2017
ABSTRACT
A fast method based on the phase trajectory to compute DSR is developed. Firstly, the phase trajectory sensitivity has more linear effect than power angle sensitivity. According to the phase trajectory boundary function, controlling unstable equilibrium generators could be identified. The PDSR is finally obtained by the sensitivity analysis between the phase and generators’ active power. Test results on the New England 10-genrator 39-bus system are presented and prove the effectiveness of this approach.
Keywords:
The Phase Trajectory, Sensitivity Analysis, Controlling Unstable Equilibrium Mode, PDSR

1. Introduction
The dynamic security region (DSR) is defined as the set of input power space before the accident. All the injection points in the set can guarantee the transient stability of the system after a given accident. DSR is related to the network topology and expected accident of the system, but not related with the change of the base point, and can be calculated offline. For online applications, the transient stability could be quickly identified, depending on whether the current injection is within the DSR. At the same time, it is possible to compute the distance from the operating point to each boundary, which represents the security margin of the system in different directions. Compared with traditional methods such as time domain simulation, DSR can provide more comprehensive security margin and auxiliary control decision for system operators.
A large number of studies have shown that [1] [2] [3], the boundary of DSR is expressed by the upper and lower active power injection limits of each bus, and hyper planes which are composed of critical operating points injection. It is also called the practical dynamic security region (PDSR).
The methods to calculate PDSR can be divided into two categories including fitting and analytic methods. The fitting method uses a large number of critical injection points calculated by numerical simulation to fit the PDSR boundary expression [1]. But in the real large-scale power grid, the number of generators is large, and the direction of the critical point search will increase exponentially, which makes the PDSR face great difficulties in the practical process. And in the process of searching the critical point, the transient stability is generally judged by the relative power angle difference of any two generators is greater than a certain critical value. It does not consider the change of power angle and angular velocity of the generator when adjusting active power of generators. This critical point search algorithm ignores a lot of useful information.
Analytic method is the use of transient stability direct method to quickly calculate the PDSR boundary [2]. In paper [2], the critical hyperplane of PDSR corresponds to the instability mode of the system. In paper [3], the PDSR boundary of different unstable modes is calculated. In paper [4], the analytical expression of the DSR is calculated by the applying property that the transient stable boundaries at different critical injection powers at the controlling unstable equilibrium point (CUEP) is approximate parallel. In paper [5], the approximate parallel property of the transient stability domain boundary is extended to the spillover point, and a practical method of DSR is given by applying the transient energy function, CUEP and the direct method of trajectory in the relevant fault. However, the direct method generally has the drawbacks of complex method and low calculation precision. Especially in the large power grid, the complex operating environment is not conducive to the establishment of the energy function.
In paper [5], the approximate parallel property of the transient stability domain boundary is extended to the spillover point, and a practical method of DSR is given by applying the transient energy function, CUEP and the direct method of trajectory in the relevant fault. However, the direct method generally has the drawbacks of complexity and low calculation precision. Especially in the large power grid, the complex operating environment makes it difficult to the establishment of the energy function.
In recent years, with the construction and development of the PMU and WAMS in the electrical power system, it has become possible to obtain the generator trajectory information in real time [6] [7]. The real-time responsive trajectory of the generator directly reflects the transient stability characteristics of the power system. The transient stability analysis and control based on the measured trajectory information are accurate and independent of the model and parameters of generators. In papers [7] and [8], a method, is proposed to judge the transient stability of power system according to the generators’ phase trajectory of real-time system. It has simple and flexible features. In paper [9], a phase trajectory judgment method based on reduced dimension transformation of power angle space is proposed, which has the advantage of not relying on the result of grouping.
In this paper, a method to calculate the PDSR boundary is proposed. It uses the generators’ phase trajectory including the power angle δ and angular velocity ω. Based on the transient stability criterion of the phase trajectory [7] [8], it proves that the sensitivity analysis method of the phase trajectory function f has better linearity than the power angle sensitivity when approaching the unstable equilibrium point in the single-machine infinite system. Then in the multi-machine system, the sensitivity matrix S based on the phase trajectory function f is proposed according to the multi-machine system phase trajectory instability criterion. Finally, the practical dynamic region is established at the unstable equilibrium point according to the sensitivity of the boundary function f.
2. The Phase Trajectory Analysis
2.1. The Stability Criterion of Phase Trajectory in Single-Machine Infinite System
The motion equation of single machine infinite system could be expressed as:
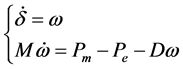 (1)
(1)
where δ is the phase angle of generators; ω is angular velocity deviation from the synchronous electrical angular velocity. M is the inertia time constant; Pm is the generators’ mechanical power; Pe is the generators, electromagnetic power; D is the generators’ damping coefficient.
In phase trajectory analysis, the phase angle δ is the abscissa and the angular velocity ω is the ordinate. The phase trajectories of the generator are shown in Figure 1 in different fault removal times.
Figure 1. The stable phase trajectory and unstable phase trajectory.
Ignoring the damping and regardless of regulator and governor role, formulation (1) can be written:
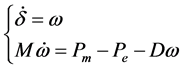 (2)
(2)
In order to study the relationship between the trend of phase trajectory and the transient stability of the system, the first order derivative D1 and the second order derivative D2 [8] of the phase trajectory are obtained:
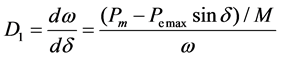 (3)
(3)
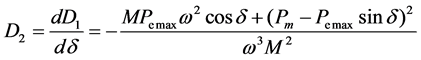 (4)
(4)
When the second order derivative D2 is 0, the formulation needs:
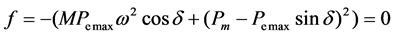 (5)
(5)
As shown in Figure 2, there is a clear boundary, affecting the trend of D1. The phase plane is divided into two parts. The left part of the second derivative has D2 < 0, and the right part of the second derivative has D2 > 0.
In paper [7], if there is no intersection between the phase trajectory and the boundary function f, the system is transient stable. The system is transient unstable when there is intersection. So for any point on the phase trajectory, the transient stability of the system can be determined according to whether the boundary function f is less than 0. Then the transient stability criterion based on the phase trajectory is:
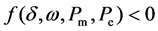 (6)
(6)
In Single-machine Infinite System, when Pm and Pe remian unchanged, for- mulation (6) shows:
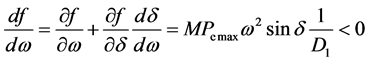 (7)
(7)
Figure 2. The phase trajectory boundary.
When ω decreases monofonicallythe phase boundary function f increases monofonically. The formulation to judge the transient stability could be writed:
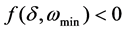 (8)
(8)
The maximum of function 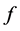 is
is 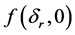 when
when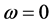 . If
. If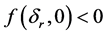 , the system is transient stable. Otherwise,the system is transient unstable.
, the system is transient stable. Otherwise,the system is transient unstable.
2.2. The Phase Trajectory Sensitivity
The traditional formulation to judge the transient stability using the phase angle:
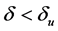 (9)
(9)
where δu is the unstable equilibrium point (UEP);
When the power system is stable:
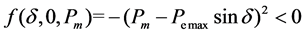 (10)
(10)
When Pm increases, 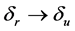 , and
, and 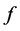 increase. So, when the system is transient stable, the two criterion is equal.
increase. So, when the system is transient stable, the two criterion is equal.
For the sake of convenience, the following Pm is denoted as P. From the above section, we know that if the system transient stability, the maximum value of f is the value of the the back point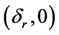
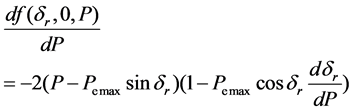
When the back point closes to the unstable equilibrium point δr → δu, we define the deceleration power
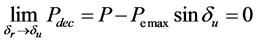
The trajectory sensitivity formula could be writen:
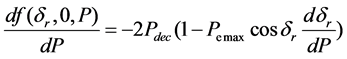
When
It can be seen that, compared with the power angle stabilitycriterion, when the generator’s active output changes, the phase trajectory stability criterion 

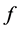
2.3. The Phase Trajectory Sensitivity in Multi-Machine System
For n generators of the power system, the movement process described as:
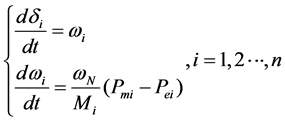
where 






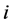
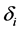
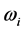
According to the above analysis, the transient stability criterion of multi-ma- chine system based on phase trajectory is shown as follows:

For the multi-machine system phase trajectory analysis, the change of active power output of generator 
For a system with n generators, a phase trajectory sensitivity matrix is defined for a certain operating point:

When the active power of generators changes ΔP, the phase trajectory formulation to judge the transient stability:

where 

For the multi-machine system, how to correctly identify the cause of system instability, in other words, how to find the cause of the system instability by
3. Construction of PDSR Based on Phase Trajectory Analysis
3.1. Practical Dynamic Security Region
The practical dynamic security region is defined [10] in power injection space:

where 




3.2. Relationship between Phase Trajectory Criterion and PDSR
In the phase trajectory analysis, the criteria to judge transient stability of the system are as follows:
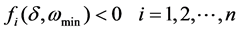
From the above analysis, combined with the sensitivity matrix S, when the generators’ active power output changes, the formula to judge transient stability system is as follows:

The formula is deformed as follows:

Comparing formula (18), we can see that formula (21) is the effective deformation of the practical dynamic security region. From paper [3], the boundary of the security region corresponds to the unstable mode of the system.
3.3. Bus Injection Constraint
The upper and lower limit of generator’ active power:
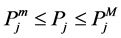
The constraints of balancing machine’ active power:

Considering the power balance of the system:

Then the bus injection constraint is given:
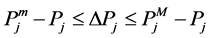

3.4. The Boundary of PDSR Based on Phase Trajectory Analysis
Substituting Equation (24) into Equation (21):

Defining the sensitivity of the phase trajectory function fi of the generator i to the generator j:

The PDSR boundary dominated by the generator i based on the phase trajectory is:

For the actual system, there are a large number of generators. The security region defined by formula (29) only needs to establish the boundary of the security domain where the critical generator is destabilized. In this case, the critical function f in the plane is only considered to be easy to be destabilized.
When adjusting active power output of the generator i to the upper limit, if the system becomes transient unstable, there is unstable mode of system controlled by generator i. And this controlling PDSR boundary is under the node injection constraint.
The dichotomy is used to search the critical point of the unstable mode. The generator set with large transient influencing factor is selected according to the sensitivity S, and selected as the coordinate axis of the reduced PDSR.
3.5. Algorithmic Flow
For the basic operation and a given fault, when the fault duration t, the algorithm flow is as follows in Figure 3:
Figure 3. PDSR Algorithm flowchart.
4. Sample
In this paper, the method proposed in the paper is tested on the New England 10-generator 39-bus system. The wiring diagram is shown in Figure 4, the system model parameters is got in literature [11].
Fault 1
This system takes the bus 31 as the balancing machine. The fault state is set as three-phase short circuit fault of 15 - 16 line in the system, cleared 0.12 seconds later.
1) The phase trajectory of the generator is obtained by time-domain simulation of the initial operating point;
2) The power angle curve of instability is obtained by increasing the failure time to t = 0.22 s, as shown in Figure 5. The critical set A = (G32, G34, G38) (G31 is the balancing machine);
3) In the critical set A, the generator’ active power output is increased to the upper limit. If the system is unstable, the controlling unstable generator G32 is identified;
4) The controlling unstable critical point of generator is searched by Dichotomy;
5) The sensitivity α is obtained based on the critical point as shown in Table 1.
Figure 4. The New England 10-genrator 39-bus system.
Figure 5. Unstable power angle curves.
Table 1. Sensitivity of generators in IEEE-39.
The PDSR with G32 as the controlling unstable mode is obtained. For the visual representation, the generator G30is selected as the auxiliary axis. The PDSR (shaded area) is shown in the Figure 6;
6) In the two-dimensional security region composed by G30 and G32, we consider the upper limit of active power output of balancing machine G31 and the upper limit of active power output of G30 and G32, and draw the two-di- mensional PDSR.
In order to verify the correctness of the DSR calculation results, several operating points are selected in the injection space of the system. The direction to choose operating points is from the basic operating point toward the G32 controlling boundary. Time-domain simulation is used to prove the accuracy of PDSR.
The corresponding unstable power angle curve as shown in Figure 7, we can see that the instability of system instability caused by the G32 generator instability.
Figure 6. PDSR controlled by G32.
Figure 7. Unstable power angle curves.
Table 2. The result of timing simulation.
In order to verify the correctness of the DSR calculation results, in the injection space of the power system, we select a number of operating pointsfrom the basic operating pointto the G32 dominant direction.Time-domain simulation is showed in Table 2.
5. Conclusion
In this paper, a method to solve practical dynamic security region is proposed based on the phase trajectory analysis. It studies the variation of the phase angle and angular velocity when the generators’ active power changes. Based on the analysis of phase trajectory stability function f and phase trajectory sensitivity matrix S, an effective relation between the criterion of phase trajectory and dynamic security region is established. The PDSR is obtained by the analysis of the phase trajectory. The result has shown that this method does not need a lot of critical points and the calculation speed is improved greatly.
Acknowledgements
This work is supported by the National Science Foundation of China (No.51377118) and the project of State Grid Tianjin Electric Power Company (KJ15-1-08).
Cite this paper
Gao, Y., Chang, J.T., Qin, C., Zeng, Y., Liu, Y.Y. and Li, S.W. (2017) Practical Dynamic Security Region Based on Phase Trajectory. Energy and Power Engineering, 9, 503-514. https://doi.org/10.4236/epe.2017.94B056
References
- 1. Zeng, Y.L., Fan, J., Yu, Y., et al. (1990) Practical Dynamic Security Regions of Bulk Power Systems. Automation of Electric Power Systems.
- 2. Yu, Y. (1990) Practical Dynamic Security Regions of Power Systems. Proceedings of the CSEE.
- 3. Min, L., Yu, Y., Lee, S.T., et al. (2004) Identification Method of Instability Modes and Its Application in Dynamic Security Region. Automation of Electric Power Systems, 28, 28-32.
- 4. Zeng, Y. and Yu, Y. (2002) A Practical Direct Method for Determining Dynamic Security Regions of Electrical Power Systems. Power System Technology, Proceedings. Power Con 2002. International Conference on. IEEE, 2, 1270-1274.
- 5. Xue, A.C., Mei, S.W., Qiang, L.U., et al. (2005) Approximations for the Dynamic Security Region of Network-reduction Power System. Automation of Electric Power Systems, 29, 18-23.
- 6. Chang, N.C., Zhou, L., Gan, D.Q., et al. (2005) A Survey on Applications of Wide-Area Measurement System in Power System Analysis and Control. Power System Technology, 29, 46-52.
- 7. Zhang, B., Yang, S. and Wang, H. (2014) Closed-loop Control of Power System Transient Stability (1): Transient Instability Detection Principle of Simple Power System. Electric Power Automation Equipment, 34, 1-6.
- 8. Gu, Z.Y., Yong, T., Sun, H., et al. (2013) An Identification Method for Power System Transient Angle Stability Based on the Trend of Rotor Speed Difference-rotor Angle Difference. Proceedings of the Chinese Society of Electrical Engineering, 33, 65-72.
- 9. Cen, B., Tang, F., Liao, Q., et al. (2015) Transient Stability Detection Using Phase Trajectory Obtained by Dimension Reduction Transform of Power Angles. Proceedings of the Chinese Society of Electrical Engineering, 35, 726-2734.
- 10. Yu, Y. (2003) Methodology of Security Region and Practical Results. Journal of Tianjin University (Science and Technology), 36, 525-528, 2003.
- 11. Pai, M.A. (1989) Energy Function Analysis for Power System Stability. Kluwer Academic Publishers, Boston. https://doi.org/10.1007/978-1-4613-1635-0









