Energy and Power Engineering
Vol.09 No.04(2017), Article ID:75299,14 pages
10.4236/epe.2017.94B043
Fast Calculation Method of Energy Flow for Combined Electro-Thermal System and Its Application
Shuxin Liu1, Sai Dai2, Qiang Ding2, Linxian Hu1, Qixiang Wang1
1School of Electrical Engineering & Automation, Harbin Institute of Technology, Harbin, China
2China Electric Power Research Institute, Beijing, China




Received: February 24, 2017; Accepted: March 30, 2017; Published: April 6, 2017
ABSTRACT
In recent years, Combined electro-thermal system has developed rapidly. In order to provide the initial data for the analysis of the combined electro-thermal system, a practical energy flow calculation method for the combined electro-thermal system is proposed in this paper. Based on the detailed analysis of the topology structure of the heating network and its hydraulic and thermodynamic model, the forward-backward sweep method for the heat flow of the heating network is established, which is more suitable for the actual radial heating network. The electric and thermal coupling model for heating source, such as thermoelectric unit and electric boiler is established, and the heat flow of heating network and the power flow of power grid are calculated orderly, thus a fast calculation method for the combined electro-thermal system is formed. What’s more, a combined electro-thermal system with two- stage peak-shaving electric boiler is used as the example system. This paper validates the effectiveness and rapidity of this method through the example system, and analyzes the influence for the energy flow of combined electro-thermal system caused by the operating parameters such as the installation location of electric boiler, the outlet water temperature of heat source and the outlet flow rate, etc.
Keywords:
Combined Electro-Thermal System, Energy Flow, Recursive Heat Flow Model for Heating Network, Electric and Thermal Coupling Model

1. Introduction
Heating network uses the heating pipes to transport steam or hot water, so as to achieve the purpose of transmitting energy. Heating source can use fossil fuels, renewable energy, electricity, cogeneration source, etc, so that it has great flexibility. Heating network and power grid are coupled into a system when cogeneration sources or electric boilers are used as heating source, thus a combined electro-thermal system is formed. The combined electro-thermal system is a typical multi-energy flow network system, which is also an important part of the energy of Internet [1].
Power flow calculation is very mature, derived out a variety of power flow calculation methods, such as Newton Raphson method, PQ decomposition method and so on [2] [3] [4]. In [5] [6], the concept and characteristics of power flow calculation in distribution network are introduced, and the mathematical model of radial power flow calculation in distribution system is summarized. In [7], for AC and DC systems, the inequality constraints are introduced to reflect the operation constraints and DC control methods. Different from the mature power flow calculation, at present there is little research involved the energy flow for combined electro-thermal system. Internationally, Nordic countries with strong electro-thermal coupling network, such as Denmark, Sweden and other countries, have made some researches on the energy flow calculation for the combined electro-thermal system. Several methods of modeling heating networks are proposed in [8] and [12]. In [9], a more complete heating network model is established, but it does not take into account the radial characteristics of the actual heating network and can’t be solved quickly and simply. There is huge computational complexity in the existing complicated calculation method of energy flow for combined electro-thermal system. In this paper, the hydrodynamic and thermodynamic models of the heating network are studied, the radial structure of the heating network is analyzed, and the recursive model of the heating network is established. The calculation mode and the calculation process of the forward-backward sweep method are also given. Then this paper studies the electric and thermal coupling model and the fast calculation method of energy flow for the combined electro-thermal system. Finally, the energy flow analysis for a combined electro-thermal system with two-stage peak-shaving electric boiler is carried out. At the same time, the influence of operating parameters, such as electric boiler installation location, outlet water temperature and outlet water flowrate of heating source node on the combined energy flow are also studied.
2. The Model of Heating Network
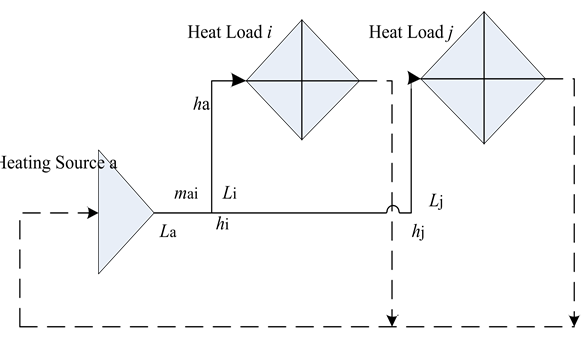
The heating network consists of the water supply network and backwater network which are the same topology [8] [12], the structure diagram is shown in Figure 1.
There are three variates in the heating network, including the pressure of each node hi, the load demand water Li, the water flow pipe mij. Due to pipe roughness, hot water in the pipes have to overcome the wall during the heat transfer process, coupled with the pipe heat dissipation outside, the hot water transferring
Figure 1. The structure diagram of heating network.
from the heating source to the heat load node will have heat loss. In the heat load node i, the hot water provides users with heat through the heat exchanger, and then the cooling water return to heating source through the return network, and the next heating process will start. The pipe water flow of supply or return network is almost the same. As the water temperature in the two networks is different from each other, it will affect the water density, viscosity, Reynolds number [9] [10] [11], resulting in the water flow of two network slightly different. In order to simplify the calculation, this paper neglects these factors [12].
2.1. The Hydrodynamic Model of Heating Network
The hydrodynamic model of the heating network determines the water flow of each pipe (mij) and the injected water flow of each node (Li). The topology of water supply network is the same as the backwater network, so only the water supply network is analyzed. There are water continuity of flow equation and pressure loss equation in hydraulic model, respectively corresponding to KCL and KVL which are belong to electrical power system [9] [13] [14].
1) Continuity of Flow Equation
The continuity of flow is expressed as: the water flow that enters into a node is equal to the water flow that leaves the node plus the flow consumption at the node. For the entire hydraulic network, the continuity of flow is expressed as
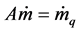 (1)
(1)
where A is the network incidence matrix that relates the nodes to the branches; m is the vector of the water flow (kg/s) within each pipe; mq is the vector of the water flow (kg/s) through each node injected from a source or discharged to a load.
2) Pressure Loss Equation
The pressure loss equation is used to characterize the relationship between pressure loss and water flow in the pipe [9], just like that
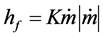 (2)
(2)
where K is the vector of the resistance coefficients of each pipe. K generally depends largely on the diameter of a pipe. The specific formula is
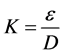 (3)
(3)
where ε is the absolute roughness value of each pipe; D is the diameter of each pipe.
Hydraulic model can be regarded as a common water pipe network, there are two basic methods of solving the water network, that is, pressure method [10] [12] [13] and circulation method [13] [15]. As there are almost branch type in the heating network and little loop type, it is suitable for heat flow calculation to adopt the general pressure method instead of circulation method [12].
2.2. The Thermodynamic Model of Heating Network
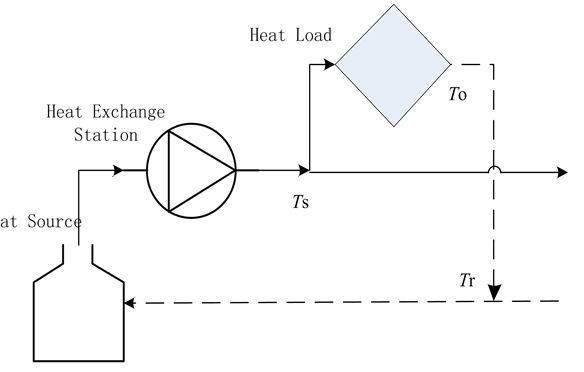
Thermodynamic model is used to determine the temperature of nodes in heating network. The heating network node contains three temperature information (Figure 2): the supply (load input) temperature of node (Ts); the return (load output) temperature of node (To) and the return mixing temperature (Tr). The return temperature of node (To) is the temperature at which the water flow leaves the junction where the heat load node does not meet the confluence duct. If there is no confluence pipe in the thermal circuit, the return temperature of node (To) is the same as the return mixing temperature. The main factors that affect the node return temperature are: the supply temperature of node (Ts), the natural temperature of the outside surrounding (Ta) and the size of the heat load.
To sum up, using the hydraulic model to calculate the water flow data of each pipe, the three temperature information of the heating network nodes are determined by the thermal model considering the heating network relation, heat transfer and heat loss.
2.3. The Heating Network Model
The heating network could be get by integrating hydraulic model and thermodynamic model. The variates relations in the heating network model are
Figure 2. The temperature diagram of each node.
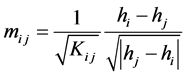 (4)
(4)
The relationship for heat load, temperature, and water flow is
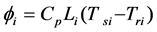 (5)
(5)
where 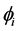 is the heat load of node; Cp is the specific heat capacity of water.
is the heat load of node; Cp is the specific heat capacity of water.
The return temperature of node is
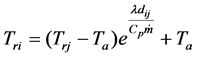 (6)
(6)
The supply temperature of node is
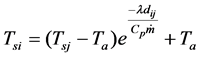 (7)
(7)
where λ is the transmission impedance per meter of the pipe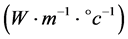 ; dij the pipe transmission distance (m).
; dij the pipe transmission distance (m).
The pressure of water supply (h) can be deduced by Equation (4).
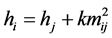 (8)
(8)
From Equation (6), Equation (7), we can see that the greater the pipe water flow, the less heat loss in the pipe, the higher the temperature of the destination node.
The thermodynamic model determines the temperature data of each node, the hydraulic model determines the water flow of each pipe, and the output data of the two systems are input to each other. For the heat flow calculation, the thermodynamic model and the hydraulic model are indispensable.
3. Fast Calculation Method of Energy Flow for Combined Electro-Thermal System
The combined electro-thermal system can be regarded as the coupling of the heating network and the electrical network through the energy conversion equipment (thermoelectric unit, electric boiler, etc.)
3.1. The Recursive Heat Flow Model for Heating Network
The purpose of heat flow calculation is to determine the water flow in the pipeline, the supply temperature of nodes and the return temperature of nodes, and finally determine the total heat supply of the heating source.
3.1.1. The Characteristics of the Actual Heating Network Structure
In actual production, each heating source (such as a thermoelectric unit) is fixedly supplied with a specific area heat load. The heating sources are either not connected or connected but the pipes are normally closed, which makes the heating network similar to power distribution network which is typical radial structure (Figure 3).
The actual heating network control method is divided into two kinds which are qualitative conditioning and volume conditioning. Qualitative conditioning
Figure 3. The actual network structure of heating network.
remains the heating source node outlet water flow rate unchanged, by adjusting the heating source outlet water temperature to adapt to heat load changes. Volume conditioning is to maintain the heating source outlet water temperature unchanged, by adjusting the heating source node outlet water flow rate to adapt to the heat load changes. The valve in volume conditioning acts frequently so that there will be more loss of the valve. Therefore, it is generally to take the method of qualitative conditioning.
3.1.2. The Recursive Heat Flow Model for Heating Network
Considering the characteristics of the heating network model and the actual structure of the heating network, the following recursive heat flow network model can be obtained.
 (9)
(9)
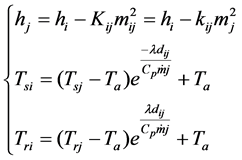 (10)
(10)
From the above analysis, the actual heating network structure and its model are similar to the power distribution network, so the forward-backward sweep method can be used to calculate the heating flow.
Forward: using the load information of each node, the water flow of each pipe and the injected water flow of each node is determined by using Equation (9) forward from the terminal node against the hot water transfer direction.
Backward: according to the direction of hot water transfer, starting at the heating source node, Equation (10) is used to determine the supply temperature, return temperature, pressure and other information of each heat load node, which the water flow information could be obtained by the forward process.
3.1.3. The Heat Flow Calculation Process of Heating Network
1) Initialize all node supply temperature and outlet water flow rate.
2) Forward calculation: calculate the heat load node injected water flow, the water flow of each pipe.
3) Backward calculation: the calculation of the heat load node supply temperature, return temperature and node pressure.
4) Calculate the return temperature of the heating source node.
5) Iterative convergence judgment. The process would output outcome if the error is within the allowable range, otherwise return to the second step.
6) Calculate the heating power of each heating source.
3.2. The Calculation Model of Electro-Thermal Coupling
After using extraction condensing turbine, electric boilers and other energy conversion equipment, power grid and heating network are tightly coupled.
1) The extraction condensing turbine can be equal to the back pressure turbine coupling with straight condensing turbine, the equivalent back pressure turbines are the main heating source. The relationship between electrical power and thermal power which are generated by back pressure turbine is expressed as
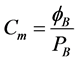 (11)
(11)
where 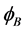 is the thermal power generated by back pressure turbine; PB is the electrical power generated by back pressure turbine; Cm is a constant which are the ratio between heat production and electricity.
is the thermal power generated by back pressure turbine; PB is the electrical power generated by back pressure turbine; Cm is a constant which are the ratio between heat production and electricity.
2) As a supplementary heating source (such as peaking heat), electric boiler produces heat energy by using electrical power which are provide by power grid.
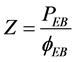 (12)
(12)
where PEB is the power consumption by electric boiler; 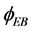
3.3. Power Flow of Power Grid
After heat flow calculation, we could get the power generated by back pressure turbine and the power consumed by electric boiler by Equation (11) and Equation (12). Then, the Newton-Raphson method is used to calculate the power flow. Since the Newton-Raphson method is very mature [16] [17] [18] [19], this paper does not repeat them.
4. Energy Flow Analysis of the Combined Electro-Thermal System with Peak-Shaving Electric Boiler Installed in Secondary Heating Network
Combined electro-thermal system with peak-shaving electric boiler installed in secondary heating network is to install electric boiler at the secondary network side of each heat exchange station. The main heating source is thermoelectric unit (extraction condensing turbine), satisfied the basic heat load, and the electric boiler is the supplementary heating source, satisfied the peak heat load [8] [9]. During the winter heating period, the “peak” of the heat load of the thermoelectric unit is used to cut the “valley” of the load of the power grid, so that the economy of the combined electro-thermal system can be improved.
4.1. The Example System
The heating network of the example system consists of two independent heating networks, as shown in Figure 4. The IEEE 5 machine with 14 nodes model is used as power grid example system. The heating source nodes (S1, S2) in the heating network part is correspond to nodes No. 10 and No. 11 in the grid respectively. The peak-shaving electric boiler is installed on nodes No. 2 and No. 11 of the heating network, peak shaving ratio (K) is 0.4.
4.2. The Results of Energy Flow Calculation
The outlet water temperature of the heating source nodes is set at 130˚C, and the outlet water flow rates of pipes No. 2 and No. 11 are 2.3, 3.4 (kg/s). Since the two heating networks are independent of each other, the trend of heat flow is similar when the operating conditions changed. Therefore, this paper only lists the heat flow calculation results of S1 heating source network.
We can see from Table 1 and Table 2, the pipe water flow decreases from the heating source node to the final node. When the heat load node is close to the heating source node, the supply temperature and the node water pressure are higher, and the return temperature is lower. Table 3 shows the power flow, as the control group data.
4.3. The Effect of Electric Boiler Position on Combined System Energy Flow
The electric boiler is installed in the head end of the heating network (No. 2, 11
Figure 4. The topological structure of heating network.
Table 1. The heat flow result of heating network.
Table 2. The result of heating network nodes.
Table 3. The result of power flow.
node), middle (No. 7, 16 nodes) and the end (No. 9, 19 nodes) in turn, and these electric load is borne by nodes No. 1 and No. 2 in the power grid respectively.
Remaining peak shaving ratio and heating source output temperature unchanged, the results of the combined system energy flow calculation compared with control group was shown in Figure 5 and Figure 6.
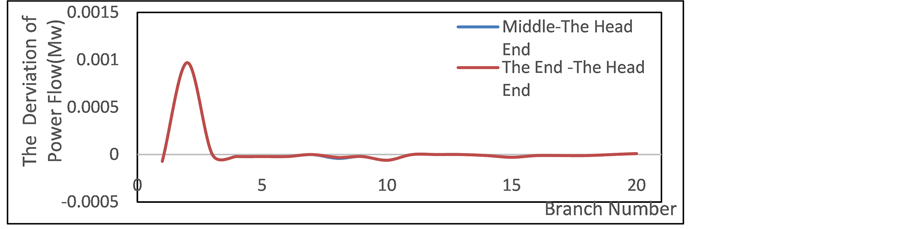
In Figure 5, to change the installation location of the electric boiler heating network will have a certain impact on the water flow in the pipe, and an electric boiler installed in the vicinity of the heat load would make the pipe flow of water suffered a greater impact. As the electric boiler installed in the No. 7, No. 9 node, corresponding to a significant peak at No. 7, No. 9 pipe to verify the correctness of the power flow calculation. It can be seen from Figure 6, in addition to the No. 2 electric load node, the bias of branch power caused by changing the location of the installation of electric boiler is almost zero, indicating that it plays a little role on branch power flow, because that changing electric boiler installation location does not alter the electrical load balance of the grid constitutionally. So we can see that two line are covered with each other.
4.4. The Effect of Outlet Water Temperature of Heating Source on Combined System Energy Flow
The heating network adopts the qualitative conditioning, and in the case that the outlet water flow rate of the heating source node is kept constant, the heat balance of the heating network is realized by adjusting the outlet water temperature. Assuming that the outlet water temperatures are 110˚C, 120˚C, and 130˚C, the results are shown in Figure 7 to Figure 8:
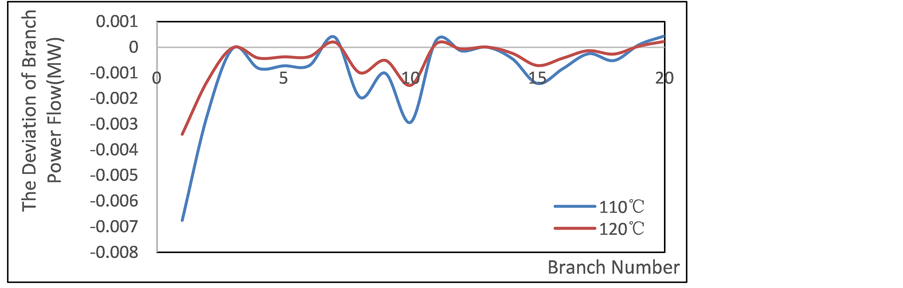
It can be seen from Figure 7 that when the outlet water temperature of the heating source is changed, the water flow of the pipe will fluctuate. The larger the temperature change is, the greater the fluctuation is, but the water flow
Figure 5. The deviation (caused by electric boiler location) of water flow in heating pipe.
Figure 6. The deviation (caused by electric boiler location) of power flow.
Figure 7. The deviation (caused by outlet temperature of heating source) of water flow in heating pipe.
Figure 8. The deviation (caused by outlet temperature of heating source) of branch power flow.
deviation is only about 3 decimal places. Using qualitative conditioning limit heating source outlet water flow rate to a certain numerical value, in order to meet the balance of heating network can only be achieved by changing the heating source return temperature. We can see from Table 4, since the heating source outlet water flow rate is limited, the heating source return temperature also decreases while the heating source outlet water temperature decreased, in line with the actual.
In Figure 8, compared to Figure 6, the results of power flow show that the change in the temperature of the outlet temperature will affect the power flow results, this is because the change in heating source outlet temperature will make the pipe heat loss changing, thus changing the total of thermal power generated by heating source, we can see that the active power output will also change by Equation (11), thus to affect the power flow results.
4.5. The Effect of Outlet Water Flow Rate Heating Source on Combined System Energy Flow
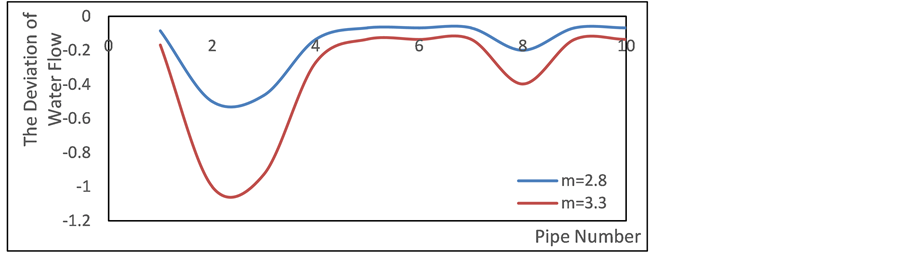
Assumed that the water temperature at the outlet of the heating source is constant, the effect of the outlet water flow on the combined system energy flow is studied. The outlet water flow rates of pipes No. 2 is set to 2.3, 2.8 and 3.3 (kg/s), and the other conditions are kept unchanged. The results of comparison with the control group are obtained as shown in Figure 9 to Figure 10.
In Figure 9, it is obvious that changing the heating source outlet water flow rate can significantly affect the water flow in the pipe. After changing the outlet water flow rate of heating source, changing the return temperature is taken to achieve the purpose of maintaining the thermal network heat balance, as shown in Table 5.
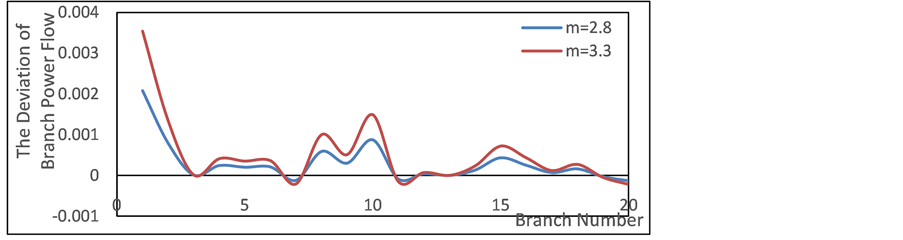
In Figure 10, changing the heat source outlet water flow rate is similar to changing the outlet water temperature, which affects the heat loss in the pipe
Table 4. The chart of return temperature corresponded to outlet water temperature of heating source.
Table 5. The chart of return temperature corresponded to outlet water flow of heating source.
Figure 9. The deviation (caused by outlet water flow rate of heating network) of water flow in heating pipe.
Figure 10. The deviation (caused by outlet water flow rate of heating network) of branch power flow.
transmission process. The active power output of the thermoelectric unit will be changed, which will affect the power flow, and the greater the variation of the outlet water flow rate, the greater the deviation of the power flow.
5. Conclusions
1) In the past few years, the thermoelectric unit, electric boiler and other energy conversion equipment have make the power grid and heat network be closed to each other, so it’s necessary to analysis the power flow and the heat flow together.
2) The forward and backward calculation of the heating network can conveniently handle the multi-branch radial heating network without complex network number and no admittance matrix. What’s more, there is also has less iterations in the new method. Therefore, the proposed method is simple and fast.
3) The example analysis shows that the electric boiler installation location, the heat source outlet water flow rate and the outlet water temperature affect the water flow distribution of the heating network, and changing the water temperature and flow rate of the heat source outlet will also affect the power flow results.
Acknowledgements
This paper was sponsored by the science and technology program called “Research and Application of Key Technology for Combined Electric-thermal System Optimizing Dispatching Considering Safety and Economy” which belong to State Grid Corporation of China.
Cite this paper
Liu, S.X., Dai, S., Ding, Q., Hu, L.X. and Wang, Q.X. (2017) Fast Calculation Method of Energy Flow for Combined Electro-Thermal System and Its Application. Energy and Power Engineering, 9, 376-389. https://doi.org/10.4236/epe.2017.94B043
References
- 1. Zhang, C., Hu, L.X., Hu, J. (2013) Research on the Impact of the Proportion of Thermal Power Generating Units and Heat Load on the Wind Power Accommodation Rate. Power System Protection and Control, 23, 120-125.
- 2. Wu, X., Wang, X.L. and Li, J. (2013)A Model to Analyze Peak Load Regulation of Provincial Power System Considering Sending-out of Wind Power. Power System Technology, 6, 1578-1583.
- 3. Fan, P.F., Zhang, L.Z. andXie, G.H. (2012) Analysis Model for Accommodation Capabiliyof Wind Power with Adequacy Resources Involved in System Regulation. Power System Technology, 5, 51-57.
- 4. Long, H.Y., Ma, J.W., Wu, K. (2011) Energy Conservation Dispatch of Power Grid with Mass Cogeneration and Wind Turbines. Electric Power Automation Equipment, 11, 18-22.
- 5. Lu, Q., Jiang, H. and Chen, T.Y. (2014) Wind Power Accommodation by Combined Heat and Power Plant with Electric Boiler and Its National Economic Evaluation. Automation of Electric Power Systems, 1, 6-12.
- 6. Li, J.J., Hu, L.X. (2015) Research on Accommodation Scheme of Curtailed Wind Power Based on Peak-Shaving Electric Boiler in Secondary Heat Supply Network. Power System Technology, 11, 3286-3291.
- 7. Deng, J.L., Hu, L.X. and Li, J.J.(2016) Analysis on Mechanism of Curtailed Wind Power Accommodation and Its Economic Operation Based on Electric Boiler for Peak-load regulation at Secondary Heat Supply Network. Automation of Electric Power Systems, 18, 41-47.
- 8. Steer, K.C.B., Wirth, A. and Halgamuge, S.K. (2011) Control Period Selection for Improved Operating Performance in District Heating Networks. Energy and Buildings, 23, 605-613. https://doi.org/10.1016/j.enbuild.2010.10.029
- 9. Liu, X, Jenkins, N. and Wu, J. (2014) Combined Analysis of Electricity and Heat Networks. Cardiff University, Cardiff.
- 10. Clamond, D. (2009) Efficient Resolution of the Colebrook Equation. Industrial & Engineering Chemistry Research, 7, 3665-3671. https://doi.org/10.1021/ie801626g
- 11. Ben, H.I. and Eicker, U. (2013) Impact of Load Structure Variation and Solar Thermal Energy Integration on an Existing District Heating Network. Applied Thermal Engineering, 2, 1437-1446.
- 12. Dong, J.N., Sun, H.B., Guo, Q.L. and Pan, Z.G. (2015) From Smart Grid to Energy Internet: State Estimation for Combined Electricity and Heat Networks. Power System Technology, 6, 1635-1641.
- 13. Bargiela, A. (1984) Online Monitoring of Water Distribution Networks. Durham University, Durham.
- 14. Liu, X. (2013) Combined Analysis of Electricity and Heat Networks. PhD Thesis. Cardiff University, Cardiff.
- 15. Arsene, C.T.C. and Gabrys, B. (2014) Mixed Simulation-State Estimation of Water Distribution Systems Based on a Least Squares Loop Flows State Estimator. Applied Math Ematical Modelling, 2, 599-619. https://doi.org/10.1016/j.apm.2013.06.012
- 16. Chen, H.Y., Chen, J.F. and Duan, X.Z. (2006) Study on Power Flow Calculation of Distribution System with DGs. Automation of Electric Power Systems, 1, 35-40.
- 17. Teng, Y.F., Ning, L.H., Li, G., Wang, X.F. and Lu, M. (2014) A Power Flow Calculation Method and Steady State Characteristics of Power System with Fractional Frequency Wind Power system. Automation of Electric Power Systems, 22, 56-62+84.
- 18. Wang, Y.P., Han, X.S., Sun, D.L., Li, Y.Y., Chen, Y., Li, D.Y., et cl.( 2015) A Power Flow Algorithm Based on Minimum Jacobian Matrix for AC/DC Hybrid Systems. Automation of Electric Power Systems, 7, 1-6.
- 19. Lu, Z.G., Zhang, J., Cheng, H.L. and Bao, F. (2012) Multi-agent State Estimation Based on Decomposition and Coordination and External Network Concentration Equivalence. Automation of Electric Power Systems, 14, 35-40.