Energy and Power Engineering
Vol.09 No.04(2017), Article ID:75279,9 pages
10.4236/epe.2017.94B031
Identification of Critical Lines in Power System Based on Optimal Load Shedding
Mingshun Liu1, Lijin Zhao1, Liang Huang1, Xiaowei Zhang2, Changhong Deng2, Zhijun Long2
1Guizhou Power Grid Co., Ltd., Guiyang, China
2School of Electrical Engineering, Wuhan University, Wuhan, China




Received: February 26, 2017; Accepted: March 30, 2017; Published: April 6, 2017
ABSTRACT
Based on risk theory, considering the probability of an accident and the severity of the sequence, combining N-1 and N-2 security check, this paper puts forward a new risk index, which uses the amount of optimal load shedding as the severity of an accident consequence to identify the critical lines in power system. Taking IEEE24-RTS as an example, the simulation results verify the correctness and effectiveness of the proposed index.
Keywords:
Risk Theory, Optimal Power Flow, Load Shedding, Risk İndex, Critical Line Identification

1. Introduction
Many blackouts have taken place in the world these years, such as the large scale blackout in interconnected north America Power Grid on August 14th and the blackout in UCTE Grid on November 4th [1] [2], which led to huge economic losses and impact upon the whole society. Previous major blackouts show that cascading failures caused by simple faults can have disastrous consequences. Therefore, it is very important to identify the critical lines in the power system to the safe and stable operation of the power system.
The use of the hidden fault model that the failure of the line will cause at least one of the other lines connected to break to identify the critical lines [3]. The power flow transferring index is proposed to identify the critical lines in cascading failures of power system [4]. Based on the small world model, a new method based on the power flow analysis is proposed to identify the vulnerable lines in the network [5]. The concept of the electrical betweenness of transmission lines whose physical background is more suitable for the power system. is proposed to identify critical lines [6]. Based on the electrical betweenness, the power flow betweenness is put forward, which is applied to identify the key lines [7].
In this paper, based on the path following method and the risk theory, a method for identifying the critical line of power system is proposed. This method is based on the nonlinear optimization model of the optimal load shedding of AC power flow, taking the amount of optimal load shedding as the severity of accident consequence, considering the probability of accident, to identify critical lines in power system. Taking IEEE24-RTS as an example, the simulation results verify the correctness and effectiveness of the proposed index, which has certain guiding significance for the power system planning, design and safe operation.
2. Risk Theory
2.1. Brief
The risk theory is a comprehensive consideration of the probability of the accident and the severity of its consequences, which is widely used in the power system risk assessment and vulnerability assessment. Based on the risk theory, the risk assessment of voltage collapse is carried out from two aspects: the probability of voltage collapse and the influence of voltage collapse [8]. Using the risk theory, the frequency deviation, voltage deviation, power angle stability margin and fault removal time margin are quantified to evaluate the transient voltage stability [9]. Based on the Bayesian network and risk theory, measure the severity of N-K fault in power system [10]. Based on the complex network theory and risk theory, the electrical betweenness is introduced into the severity index of the failure consequence to assess the risk in power system [11].
The equation of risk theory is:
 (1)
(1)
In the Equation (1), R represents the risk index of the accident; P represents the probability of the accident; S represents the severity of the accident.
2.2. Probability of Accident
The probability of accident is random, because of the random fluctuation of the load level, the random fluctuation of the new energy and the uncertainty of the external factors. It can be seen from the statistics that the probability of the power system accident is basically in accordance with the Poisson distribution [12]:
 (2)
(2)
In the Equation (2), λi is the rate of accident Ei.
3. Optimal Load Shedding
3.1. Interior Point Method
The interior point method is the most widely used algorithm for solving optimal power flow model, can be used in linear programming, two programming and nonlinear programming. There are two kinds of algorithms, such as affine scaling method and path following method. The path following method is widely used in power system because of its fast convergence speed, strong robustness and insensitivity to initial value selection [13].
3.2. Optimal Load Shedding Model
Based on the optimal power flow algorithm in [14], using the generator busactive power PG, generator bus reactive power QG, load bus PD and QD as control variables, the optimal load shedding model is proposed:
 (3)
(3)
In the equation, PGi, QGi represents the generator active power and reactive power output; PDi, QDi represents the load active power and reactive power; Pi, Qi represents the bus active power and reactive power; PCi, QCi represents the active power and reactive power of load shedding; Vi represents the voltage amplitude; Sij represents the apparent power of line i-j; NLd represents the number of transmission lines.
4. Critical Lines Identification
According to the risk theory and the optimal load shedding model, the flow chart of critical lines identification in power system is shown in Figure 1.
The following are the main steps:
1) Obtain the basic data of the system, including technical data, operating constraints, line fault data, etc.
2) Use the interior point method to calculate the amount of optimal load shedding of N-1 and N-2 security check.
3) Calculate the amount of optimal load shedding of each line according to Equation (4).
 (4)
(4)
In the Equation (4), CCi represents the comprehensive amount of optimal load shedding of line i; j represents the optimal load shedding associated with line i; f represents the amount of optimal load shedding of N-1 and N-2 security
Figure 1. Flow chart of critical lines identification.
check.
4) Calculate the probability of each line accident according to Equation (2).
5) Based on the risk theory, considering the probability of the accident and the severity of the consequences, calculate the risk index of each line according to Equation (5).
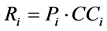 (5)
(5)
In the Equation (5), Ri represents the risk index of line i; Pi represents the probability of line i accident.
6) Obtain the critical lines in power system by listing the risk index in descending order.
5. Simulation Results and Analysis
5.1. Summary
In this paper, IEEE24-RTS is taken as an example for simulation calculation, which consists of 33 generators, 17 load buses, 38 transmission lines, the total installed capacity of 3000.00 MW and the total load capacity of 2850.00 MW. The Electrical connection diagram of IEEE24-RTS is shown in Figure 2. The low voltage reactor capacity of bus 6 is 100 Mvar. Therefore, when the voltage of bus
Figure 2. Electrical connection diagram of IEEE24-RTS.
6 is low, the priority is to reduce the reactor capacity of bus 6.
5.2. Optimal Load Shedding of N-1 Security Check
Using the deterministic method, disconnect a line in turn to simulate the three-phase permanent fault of the line. Then use the interior point method to calculate the amount of optimal load shedding. The simulation results are shown in Table 1.
The table shows that the IEEE24-RTS does not conform to the traditional N-1 security check. When the tenth line of the system is disconnected because of the fault, the voltage of bus 6 will decrease, resulting in the relay protection action and the bus load is reduced. Considering the total reactor capacity and 41.4 + j8.53 of the amount of bus 6 load shedding, the amount of optimal load shedding is 116 MVA. When the 27th line of the system are disconnected because of the fault, the voltage of bus 3 and bus 24 will decrease. The amount of optimal load shedding is 45 MVA.
Table 1. Optimal load shedding of N-1 security check.
5.3. Optimal Load Shedding of N-2 Security Check
Using the deterministic method, disconnect two lines in turn to simulate the three-phase permanent fault of the line. Then use the interior point method to calculate the amount of optimal load shedding. The simulation results are shown in Table 2.
It can be seen from Table 2 that the tenth line is an extremely important line, because that provided the N-2 fault associated with the tenth line, the amount of optimal load shedding at least is 116 MVA. Compared with Table 1, we can see that when the N-2 fault occurs, the chance of load shedding is obviously increased, and the amount of optimal load shedding is also significantly increased, so the occurrence of N-2 fault should be avoided.
5.4. Critical Line and Its Risk Index
Combining the amount of optimal load shedding of N-1 and N-2 security check, calculate the comprehensive amount of optimal load shedding according to Equation (4). Considering the probability of the accident, calculate the risk index of each line according to Equation (5). The results are shown in Table 3.
From Table 3, it can be seen that the first 10 critical lines of IEEE24-RTS contain two 230 kV lines, the whole five 138/230kV transformer power transmission lines and two 138 kV lines. The two lines with the highest risk index are consistent with the optimal load shedding order of N-1 security check. Line 10 is the highest degree of risk in the system, and does not meet the N-1 security check, and it should be redesigned.
The first 10 critical lines concentrated in the 230 kV lines and 138/230kV transformer power transmission lines, indicate that the higher the line voltage level, the higher the degree of the risk. The transformer power transmission lines are important channels, once the fault occurred to these lines, it will affect the power transmission and stability and the comprehensive risk degree is high. The system includes 4 sets of 230 kV double circuit lines. And Table 3 shows the double circuit lines in the same tower are more prone to N-2 fault, while the comprehensive risk indexes of which are low and the reliability of which is high.
The bar graph of IEEE24-RTS risk index is shown in Figure 3.
6. Conclusion
Based on risk theory, considering the probability of an accident, this paper puts forward a new risk index, which uses the amount of optimal load shedding of N-1 and N-2 security check as the severity of an accident consequence to identify
Table 2. Optimal load shedding of N-2 security check.
Table 3. Critical line and risk index of IEEE24-RTS.
Figure 3. Risk index of IEEE24-RTS.
the critical lines in power system. Taking IEEE24-RTS as an example, the simulation results verify the correctness and effectiveness of the proposed index
The proposed index has certain guiding significance for the power system planning, design and safe operation, and provides reliable reference for the power system operation and maintenance personnel.
The higher the line voltage level, the higher the degree of the risk. And the transformer power transmission lines are important channels, the comprehensive risk index of which is high. Therefore, the operation and maintenance personnel should pay close attention to the higher voltage level and transformer power transmission lines to ensure the security and stability of power system in the process of electric power production.
Fund
Technology Major Project of China Southern Power Grid Co., Ltd. (GZ2014- 2-0049).
Cite this paper
Liu, M.S., Zhao, L.J., Huang, L., Zhang, X.W., Deng, C.H. and Long, Z.J. (2017) Identification of Cri- tical Lines in Power System Based on Optimal Load Shedding. Energy and Power Engineering, 9, 261-269. https://doi.org/10.4236/epe.2017.94B031
References
- 1. Yin, Y.H., Guo, J.B., Zhao, J.J., et al. (2003) Preliminary Analysis of Large Scale Blackout in Interconnected North America Power Grid on August 14 and Lessons to Be Drawn. Power System Technology, 27, 8-16.
- 2. Gao, X., Zhuang, K.Q. and Sun, Y. (2007) Lessons and Enlightenment from Blackout Occurred in UCTE Grid on November 4, 2006. Power System Technology, 31, 25-31.
- 3. Ding, L.J., Liu, M.J., Cao, Y.J., et al. (2007) Power System Key-lines Identification Based on Hidden Failure Model and Risk Theory. Automation of Electric Power Systems, 31, 1-5, 22.
- 4. Zeng, K.W., Wen, J.Y., Cheng, S.J., et al. (2014) Critical Line Identification of Complex Power System in Cascading Failure. Proceedings of the Chinese Society for Electrical Engineering, 34, 1103-1111.
- 5. Liu, Y.N., Shu, X., Kang, K.F., et al. (2011) Identification of Vulnerable Lines In Power Grid Based on The Weighted Reactance betweenness Index. Power System Protection and Control, 39, 89-100.
- 6. Xu, L., Wang, X.L. and Wang, X.F. (2010) Electric betweenness and Its Application in Vulnerable Line Identification in Power System. Proceedings of the Chinese Society for Electrical Engineering, 30, 33-39.
- 7. Liu, W.Y., Liang, C., Xu, P., et al. (2013) Identification of Critical Line in Power Systems Based on Flow betweenness. Proceedings of the Chinese Society for Electrical Engineering, 33, 90-98.
- 8. Chen, H.W., Jiang, Q.Y., Cao, Y.J., et al. (2005) Risk Assessment of Voltage Collapse in Power System. Power System Technology, 29, 6-11.
- 9. Liu, X.D., Jiang, Q.Y., Cao, Y.J., et al. (2009) Transient Security Risk Assessment of Power System Based on Risk Theory and Fuzzy Reasoning. Electric Power Automation Equipment, 29, 15-20. (In Chinese).
- 10. Zhang, G.H., Zhang, J.H., Yang, Z.D., et al. (2009) Risk Assessment Method of Power System N-K Contingencies. Power System Technology, 33, 11-21.
- 11. Zhao, Y., Li, H.Q., Wang, Y.M., et al. (2013) A Complex Network Theory and Conditional Probability Based Risk Assessment Method for Disastrous Accidents. Power System Technology, 37, 3190-3196.
- 12. Hua, W., McCalley, J.D., Vittal, V., et al. (2000) Risk Based Voltage Security Assess- ment. IEEE Trans on Power Systems, 15, 1247-1254. https://doi.org/10.1109/59.898097
- 13. Zhong, S.X. and Yuan, R.X. (2005) An Application of Interior Point Method in Optimization of Power Systems. High Voltage Engineering, 31, 76-79.
- 14. Hao, Y.G., Liu, G.Y. and Yu, E. (1996) A New OPF Algorithm Based on Karmarkar’Interior Point Method. Proceedings of the Chinese Society for Electrical Engineering, 16, 409-412. (In Chinese)





