Energy and Power Engineering
Vol.09 No.04(2017), Article ID:75218,10 pages
10.4236/epe.2017.94B005
An Improved FMECA Method for Wind Turbines Health Management
Mian Du1,2, Jun Yi2, Jianbo Guo2, Lin Cheng1, Shicong Ma2, Qing He2
1Department of Electrical Engineering, Tsinghua University, Haidian District, Beijing, China
2China Electric Power Research Institute, Haidian District, Beijing, China




Received: February 21, 2017; Accepted: March 30, 2017; Published: April 6, 2017
ABSTRACT
In this paper, an improved Failure Modes, Effects and Criticality Analysis (FMECA) method for wind turbine reliability investigation is proposed. According to previous work, the main deficiencies of Risk Priority Number (RPN) based criticality analysis are presented. For the qualitative analysis, failure modes and main causes of a gearbox are analyzed on subcomponents level with available data. After that, inspection approaches are provided and mitigation methods are recommended from both design and maintenance stage. For criticality analysis, another index, Probable Profit Loss (PPL) is created and all the parameters are carefully defined to overcome the limits of conventional RNP method. Moreover, to make PPL applicable for maintenance tasks, different maintenance types are considered for profit loss calculation. The criticality rank shows the efficiency of the index and can be used as reference for making maintenance schedules.
Keywords:
Wind Turbine, Criticality Analysis, Maintenance, Economic Index

1. Introduction
Wind energy has been considered as an effective sustainable resource for reducing the carbon dioxide emission and supporting the economic development. According to [1], until 2015, the cumulative installed wind capacity in the world is 432.883 GW, in which offshore wind power capacity is 12.107 GW. Figure 1 shows the cumulative global installation of wind energy in the past 5 years. The huge amount of installation shows the prosperous of global wind market. Meanwhile challenges are also emerging behind the big numbers.
One of the challenges is the reliability and safety due to the high penetration of wind energy into power systems. Under this scenario, the uncertainty of wind
Figure 1. Wind energy global annual installation from 2011-2015.
power adds a new factor which may impact the transmission grid. Another challenge is that because of the huge amount of installation of wind turbines, especially large scaled offshore wind farms, the Operation and Maintenance (O&M) investment will increase to a high level which will pull down the profit of the wind industry. One way to solve these two problems is to increase the reliability of wind turbines in both design and operation stages. To achieve that goal, many excellent works [2] [3] [4] [5] have been done.
In this area, on branch is focusing on failure analysis which is based on expertise experience and failure information. As is introduced in [2], some of the failure analysis methods and tools are: Cause-Consequence Analysis, Event Tree Analysis, Fault Tree Analysis, Hazard & Operability Analysis, Failure Modes and Effects Analysis (FMEA) and so on. FMEA is supposed to be one of the best candidates for reliability analysis for design stage and has been used for many power generation engineering systems [6]. In [7], the main advantage of FMEA can be summarized as highly consecutive and hierarchical structure. Generally, Failure Modes Effects and Criticality Analysis (FMECA) can be considered as an upgrade of FMEA because it is a two steps method which FMEA is the first step and Criticality Analysis is step 2. Therefore, FMECA method inherits the advantages of FMEA and provides new insight into reliability analysis.
In wind turbine FMECA field, [6] used FMEA for wind turbine reliability analysis and made comparison between FMEA results and field data. In [8], FMEA was applied to the design for 2 MW R80 wind turbine by comparing the reliabilities of three versions of the geared R80 with different drive train solutions. Even though the conventional FMEA method has many advantages in reliability analysis, some weak points have been presented in [2] and [9] as follows:
1). RNP numbers are determined by personal experiences and hence the results are subjective and differ with people.
2). RPN numbers generated from different wind turbines are incomparable since the configuration of wind turbines varies.
3). Even though the RPN numbers provide valuable information for criticality identification, lack of physical meaning makes it difficult to be explained.
4). From the O&M perspective, RNP needs upgrade to take economic index into consideration to show the true risk of different failure mode.
5). The failure mode which has low occurrence frequency but serious effects may generate a small RPN number leading to low criticality rank.
To improve the conventional FMECA method, authors in [10] proposed a fuzzy FMEA method for floating wind turbine risk analysis to avoid the effect of subjectivity. In [11], a risk based FMEA method was developed and incurred failure cost instead of rating scales. However, the definition of the loss of failure needs more clarification. A similar method had been proposed in [9] to compare the risk of offshore and onshore wind turbines, however, maintenance types which have impact on total cost on O&M were not considered in this paper. Authors in [12] created a fuzzy FMEA method with failure cost taken into account for offshore wind turbines. The fuzzy theory may ease the problem caused by subjectivity. However, one of the main advantages of FMEA, straightforwardness for application, could be weaken if complicated theories are adopted. Hence, to overcome the drawbacks of conventional FMEA while keeping its benefits, more work are required to be done.
Motivated by this idea, the main goal of this paper is to update the qualitative failure mode and effects analysis with available data while improving the economic index from the O&M perspective. The rest of this paper is organized in the following way. In Section 2, a qualitative analysis on wind turbine gearbox failure mode, effects, main causes and mitigation methods is presented. After that, an improved economic index for criticality identification is proposed in Section 3. In the conclusion, a summary of all the findings in this paper is presented.
2. Qualitative Analysis on Failure Modes, Effects, Main Causes and Mitigation Methods
The framework of FMEA is an open process which can be updated when new field information is available. Considering the wind turbine is under investigation, the presentative configuration of FMEA is shown as Figure 2.
Figure 2. Hierarchy structure of WT FMEA.
The determination on which level the research should stay is depended on data sufficiency and the perspective. Thanks to the excellent work in [13], more failure information of gearbox subcomponents are provided. In [6] [11] and [3], the failure analysis focused on wind turbine components level due to the lack of field data in detail. However, if considering maintenance as the main goal of FMEA, the subcomponents level is more preferable as the maintenance type is depended on which subcomponent is suffering damage [14]. From [15], failure information of wind turbine components can be summarized in Table 1. The failure frequency of gearbox does not rank high among all the components, the consequence however, ranked the first place in this case.
Therefore, in this section, gearbox is selected for subcomponents FMEA. To avoid subjectivity, the failure modes, main causes and mitigation methods of gearbox are summarized from the experiment data provided in [16]. The presentation configuration of a gearbox is shown as Figure 3. A gearbox has High Speed Shaft (HSS) Bearing, Intermediate Speed Shaft (IMS) Bearing, Low Speed Shaft (LSS) Bearing, Planet Bearing, Planet Carrier Bearing, Helical Gear, Planet Gear, Ring Gear, Internal Shafts, HSS Coupling, and Housing.
After subdivision of a gearbox, the failure information about each subcomponents is provides as Figure 4. About 48% of gearbox failures should be attributed to HSS bearing. Which means it needs more attention during both design and operation stage.
When observing the failure modes and main causes of gearbox subcomponents, bearings, gears and lubricant oil system are selected because they are basic instruments of all the subcomponents. For qualitative analysis, the first step is to clarify failure modes and the related main causes. After that, inspection and mitigation methods are recommended. The failure modes and main causes of gearbox subcomponents are shown in Table 2.
According to the failure information, the available inspection methods are
Table 1. WT failure information in [15].
Table 2. Failure modes and main causes for gearbox.
Figure 3. The presentation configuration of a Gearbox [16].
Visual inspection, Magnet on stick, Filter inspection, Metal detectors, Critical Supervisory control and data acquisition (SCADA) data trending, Vibration analysis, and Borescope inspection. Since the common contamination of lubricant are sand, rust, machining chips, grinding dust, weld splatter, and wear debris, lubricant oil condition monitoring and analysis are also very important to increase the reliability of a gearbox.
Besides that, for gearboxes which are often suffering cracks, increasing the flow rate and distribution of lubricant oil by revising the pipelines and sprayers during design stage will increase the reliability of gearboxes. From maintenance perspective, eliminating lubricant oil contamination in time with accurate oil stability analysis will mitigate failures due to oil contamination.
Figure 4. Failure rate distribution of gearbox subcomponents.
3. Quantitative Analysis: Critical Components Identification
In this section, an improved method for critical components identification is created inspired by the conventional RPN approach. Field data are adopted to avoid subjectivity and lack of physical meaning rooted in RPN method. Furthermore, to point out the interest of this work, an economic index is proposed to connect FMECA to wind turbine maintenance. From the operators’ perspective, an index is more preferable if it is easy to understand and apply. Hence, to keep the straightforwardness of the conventional RPN method and provide information that is directly related to profit, a new index named as Probable Profit Loss (PPL) is created with the general form as Equation (1).
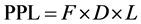 (1)
(1)
in which, F refers to failure rate, D represents undetected possibility and L denotes the profit loss. All these three parameters are calculated with field failure data and maintenance record. Moreover, this index has easy scalability due to its concise form. The first step is to define all three parameters with acceptable mathematical support. The definition of F can be written as Equation (2).
 (2)
(2)
where, f(t) refers to the time to first failure distribution and R(t) is the reliability function which means the probability of no failure before time t. Based on this form, failure rate is actually not a probability since it can exceed 1. To make it convenient for application, Nelson-Aalen estimator is used to calculate this parameter. A Nelson-Aalen estimator can be expressed as Equation (3).
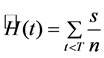 (3)
(3)
in which s is the number of events that lead to the breakdown of a certain device and n refers to the total number of devices that are included. In this work, annual failure rate of the wind turbine components is adopted for calculation.
Considering the total number of failures are constituted with two parts. One part is the failures in the record, the other one is the failures that are detected during their evolving stages with the existing inspection methods. Then the undetected possibility, i.e. D, can be calculated with Equation (4).
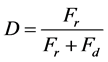 (4)
(4)
where Fr refers to the failures which actually happened in certain periods and Fd represents the failures that are prevented by inspection methods.
The most important parameter is the profit loss related to the breakdown of a certain component. This parameter has been defined in [9] and [11]. However, neither of them considered the seriousness of different failure modes which impact the choice on maintenance types. The general profit loss L can be expressed as Equation (5). For each maintenance type i,
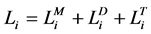 (5)
(5)
In which, 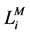 refers to the loss due to maintenance,
refers to the loss due to maintenance, 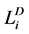 represents the loss related to delayed time, and
represents the loss related to delayed time, and 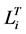 is the loss generated from transportation. All these parameters are defined with Equation (6) to Equation (8).
is the loss generated from transportation. All these parameters are defined with Equation (6) to Equation (8).
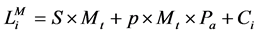 (6)
(6)
where 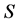 is the salary of the maintenance technicians with metric as
is the salary of the maintenance technicians with metric as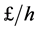 .
. 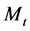 (hr) is the maintenance time. Parameter
(hr) is the maintenance time. Parameter 



In which 



where 

For components criticality identification, the maintenance related cost for component 



To verify the proposed PPL index, available field data from [14] are adopted. According to this paper, 5 maintenance types are defined in Table 3.
More information about the cost of each maintenance type for different components and the rent for typical vessels considering maintenance for offshore wind turbines are available in the appendix of [14]. After applying the PPL method, a criticality rank of wind turbine components is shown as Table 4. It is obvious that this index emphasizes the effects of components failure by introducing parameter L. Since all the data is averaged annual value, this result can also been considered as the estimated annual loss due to failures.
The PPL index implies that, although the failure rate of support and housing component is pretty low, the high profit loss and poor detection probability make it the most critical part among all the components. It recommends more research in failure detection for support and housing component and more attention during operation. Moreover, the rank list provides insight into the inspection priority when different parts are in bad condition. All the PPL results are comparable with each other even though the components are from different wind turbines because PPL means the probable loss.
To compare PPL with conventional RPN method, the criticality rank list generated from [9] and [10] is used as reference. Table 5 shows the criticality rank of components of awind turbine based on RPN method.
Despite of the different subdivision of a wind turbine, the components which rank higher in RPN rank list also gets a higher place in Table 5, such as Gearbox and Electrical system. It is inaccurate to say that Pitch Mechanism and Main shaft has the same criticality level as their RPN values equal to each other. However, if this case is observed in the PPL rank list, these two components are
Table 3. Definition of maintenance types.
Table 4. Wind turbine components criticality rank.
Table 5. RPN based criticality rank.
equally critical since PPL is an economic index with definite practical meaning and unit. It is the most important advantage because the PPL values of each components are comparable and can be used for calculation. The traditional FMEA could be suitable during the “design” stage of a new wind turbine configuration as only a relative ranking order is needed. The proposed PPL index would be suitable for risk analysis and evaluation, during operation stage. At this stage, a more detailed analysis of each failure mode is required to evaluate their ultimate effects on the system performance.
4. Conclusion
FMEA and FMECA are widely used reliability analysis methods which provide useful information for design stage. For wind turbines health management, maintenance is also an important way to increase the reliability of wind farms. In this paper, an improved FMECA method is proposed focusing on wind turbine maintenance. After analyzing failure modes and main causes of gearbox on subcomponents level with available data, inspection approaches are provided and mitigation methods are recommended from both design and maintenance stage. Moreover, PPL index is created by taking both maintenance types and profit loss related to component failure into consideration. All the parameters are carefully defined and the results show the efficiency of the proposed method. The PPL index is suitable for reliability analysis on different levels and can easily update when new field data is available. The future work is to investigate the sensitivity of PPL to the change of D parameter, which can be used as the criterion for the inspection methods applied for wind turbine failure detection.
Cite this paper
Du, M., Yi, J., Guo, J.B., Cheng, L., Ma, S.C. and He, Q. (2017) An Improved FMECA Method for Wind Turbines Health Management. Energy and Power Engineering, 9, 36-45. https://doi.org/10.4236/epe.2017.94B005
References
- 1. Sawyer, S. and Rave, K. (2015) Global Wind Report—Annual Market Update 2015. Global Wind Energy Council.
- 2. Sinha, Y. and Steel, J.A. (2015) A Progressive Study into Offshore Wind Farm Maintenance Optimisation Using Risk Based Failure Analysis. Renewable and Sustainable Energy Reviews, 42, 735-742.https://doi.org/10.1016/j.rser.2014.10.087
- 3. Carroll, J., McDonald, A. and McMillan, D. (2015) Failure Rate, Repair Time and Unscheduled O&M Cost Analysis of Offshore Wind Turbines. Wind Energy.
- 4. Kaidis, C., Uzunoglu, B. and Amoiralis, F. (2015) Wind Turbine Reliability Estimation for Different Assemblies and Failure Severity Categories. IET Renewable Power Generation, 9, 892-899. https://doi.org/10.1049/iet-rpg.2015.0020
- 5. Kim, D.H. and Lee, S.G. (2015) Reliability Analysis of Offshore Wind Turbine Support Structures under Extreme Ocean Environmental Loads. Renewable Energy, 79, 161-166. https://doi.org/10.1016/j.renene.2014.11.052
- 6. Arabian-Hoseynabadi, H., Oraee, H. and Tavner, P. (2010) Failure Modes and Effects Analysis (Fmea) for Wind Turbines. International Journal of Electrical Power & Energy Systems, 32, 817-824. https://doi.org/10.1016/j.ijepes.2010.01.019
- 7. Khorshidi, H.A., Gunawan, I. and Ibrahim, M.Y. (2016) Data-Driven System Reliability and Failure Behavior Modeling Using FMECA. IEEE Transactions on Industrial Informatics, 12, 1253-1260. https://doi.org/10.1109/TII.2015.2431224
- 8. Tavner, P., Higgins, A., Arabian, H., Long, H. and Feng, Y. (2010) Using an FMEA Method to Compare Prospective Wind Turbine Design Reliabilities. European Wind Energy Conference and Exhibition 2010, EWEC 2010, Sheffield.
- 9. Shafiee, M. and Dinmohammadi, F. (2014) An FMEA-based Risk Assessment Approach for Wind Turbine Systems: A Comparative Study of Onshore and Offshore. Energies, 7, 619-642.https://doi.org/10.3390/en7020619
- 10. Liu, Z., Sun, L., Guo, Y. and Kang, J. (2015) Fuzzy FMEA of Floating Wind Turbine Based on Related Weights and TOPSIS Theory. 2015 Fifth International Conference on Instrumentation and Measurement, Computer, Communication and Control (IMCCC). https://doi.org/10.1109/IMCCC.2015.241
- 11. Kahrobaee, S. and Asgarpoor, S. (2011) Risk-based Failure Mode and Effect Analysis for Wind Turbines (RB-FMEA). North American Power Symposium (NAPS). https://doi.org/10.1109/naps.2011.6025116
- 12. Dinmohammadi, F. and Shafiee, M. (2013) A Fuzzy-FMEA Risk Assessment Approach for Offshore Wind Turbines. International Journal of Prognostics and Health Management, 4, 59-68.
- 13. Errichello, R. and Muller, J. (2012) Gearbox Reliability Collaborative Gearbox 1 Failure Analysis Report. National Renewable Energy Laboratory, Golden.
- 14. Le, B. and Andrews, J. (2015) Modelling Wind Turbine Degradation and Maintenance. Wind Energy, 19, 571-591. https://doi.org/10.1002/we.1851
- 15. Faulstich, S., Hahn, B. and Tavner, P.J. (2011) Wind Turbine Downtime and Its Importance for Offshore Deployment. Wind Energy, 14, 327-337.
- 16. Sheng, S., McDade, M. and Errichello, R. (2011) Wind Turbine Gearbox Failure Modes: A Brief. National Renewable Energy Laboratory, Los Angeles. https://doi.org/10.1002/we.421






