Journal of Computer and Communications
Vol.05 No.03(2017), Article ID:74656,6 pages
10.4236/jcc.2017.53008
Parameter Estimation of Maneuvering Target Using Maximum Likelihood Estimation for MIMO Radar with Colocated Antennas
Hai Li, Ling Xu, Zhe Zhang
Tianjin Key Lab. for Advanced Signal Processing, Civil Aviation University of China, Tianjin, China




Received: March 2, 2017; Accepted: March 10, 2017; Published: March 13, 2017
ABSTRACT
The estimation of target parameters in MIMO radar signal processing is one of the most important research topics. An efficient implementation of the Maximum Likelihood estimator is presented in this paper to estimate the DOA (Direction of Arrival), initial velocity and acceleration of a maneuvering target in colocated MIMO radar. The target’s DOA is estimated in the first place, then a Maximum-Likelihood (ML) estimation based on peak search is applied to a two-dimensional grids providing estimation of initial velocity and acceleration. Simulations show that the MIMO radar has a better performance in DOA estimation than the phased array radar. By means of Monte Carlo simulations, the estimation error of initial velocity and acceleration on different SNRs are calculated. The results also suggest the effectiveness of this method.
Keywords:
MIMO Radar, Parameter Estimation, Maximum Likelihood Estimation

1. Introduction
The Multiple-Input Multiple-Output (MIMO) Radio Transmission Technology, has the potential to enhance system capacity and improve spectral efficiency without requiring extra emission signal bandwidth or transmission power [1] [2]. The overwhelming popularity of MIMO systems draws radar researchers’ attention to engage MIMO techniques in radar systems implementation.
MIMO radar employs multiple elements at both transmitting and receiving antennas as the phased array radar does, on flip side, MIMO radar transmits orthogonal or partially correlated waveforms. According to the antenna configura- tion, MIMO radar systems can be classified into two categories: collocated (coherent) MIMO radars are those with closely spaced antennas [3]. While distributed MIMO radars, also known as non-coherent MIMO radars, whose antennas are placed far from each other [4]. The latter configuration exploits the random fluctuation of the targets’ Radar Cross Section (RCS). This fluctuation causes spatial decorrelation between target echoes, which prevents coherent processing. It is known that spatial resolution can be improved by taking advantage of coherent processing introduced by coherent MIMO radar. Several methods have been proposed for DOA estimation offering significant estimate performance without considering Doppler effects [5] [6]. As shown in [7] and [8], parameters of moving target can be measured by the maximum likelihood estimator for distributed MIMO radar. There are many efforts have been made on joint DOA and Doppler frequency estimation [9] [10], while few studies have yet been conducted on maneuvering targets.
This paper considers parameters estimation of maneuvering target in colocated MIMO radar by developing a maximum-likelihood estimator. The MUltiple SIgnal Classification (MUSIC) is applied in the first place to estimate DOA, followed by a two-dimensional search applied to estimate the velocity and acceleration. Performance of estimation for phased array radar and MIMO radar are compared under the same condition. The root mean square errors (RMSE) of the ML estimation of target parameters are obtained by Monte Carlo simulations. Numerical results demonstrate that MIMO radar has better angle estimation performance compared with conventional phased array radar and verify the effectiveness of this method as well.
2. MIMO Radar Signal Model
Let’s consider a MIMO radar system in which there are 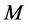 transmitting antennas and
transmitting antennas and 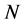 receiving antennas, with inter-element spacing of
receiving antennas, with inter-element spacing of 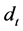 and
and , respectively. Radar working wavelength is
, respectively. Radar working wavelength is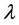 .The signal emitts from the
.The signal emitts from the 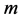 -th antenna, is defined as
-th antenna, is defined as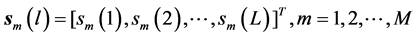 , where
, where 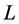 is the length of coded pulse signal, with
is the length of coded pulse signal, with  denoting the transpose of matrices. Assuming the different transmitting signals are orthogonal, then transmit steering vector of the array towards direction
denoting the transpose of matrices. Assuming the different transmitting signals are orthogonal, then transmit steering vector of the array towards direction  can be denoted as
can be denoted as
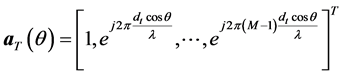 (1)
(1)
and the receive steering vector is
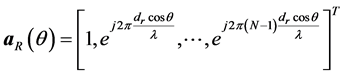 (2)
(2)
Assuming that the target has a reflection coefficient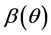 , moves with an initial radial velocity
, moves with an initial radial velocity  and an acceleration
and an acceleration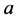 .The received signal at antenna
.The received signal at antenna  and time index
and time index 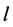 can be described by
can be described by
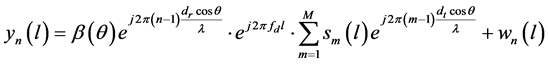 (3)
(3)
where 



The total 

where







3. Maximum Likelihood Estimation
Let 






The probability density function of 

where 

where 




The first term 








It can be easily shown that the product in (9) yields a diagonal matrix with diagonal elements maintain a constant which equals to

In order to find the maximum likelihood estimations of the unknown parameters, it is necessary to perform a three-dimensional (3-D) search in the parameter space. From a practical point of view, such a 3-D search, for all possible values of DOA, velocity and acceleration of a target, can cause tremendous computational burden. Therefore, we propose a two-stage sequential estimation process.
As we simplify the target moving scenario by assuming the target is moving along a certain direction, a classical sub-space method, multiple signal classification, is used to estimate the DOA of the target which can be treated as static or relatively static. Then the estimation of initial velocity and acceleration can be obtained when the cost function in (10) achieves its maximum.
4. Simulations
We consider a MIMO radar with 6 antennas both on transmitting and receiving ends. Antennas are uniformly spaced with an distance of












Monte Carlo simulations with 200 trials per signal-to-noise ratio (SNR) were conducted to acquire the RMSE of the ML estimation. The RMSE of DOA is shown in Figure 1, which indicates that MIMO radar has better angular estimation performance than phased array radar. The RMSE of initial velocity is shown in Figure 2, and that of acceleration is shown in Figure 3. Under various SNRs, MIMO radar and phased array radar both can obtain excellent estimation performance in estimating initial velocity and acceleration of maneuvering targets.
5. Conclusions
This paper studies the performance of parameters estimation of maneuvering target in coherent MIMO radars with the application of maximum likelihood estimation. Numerical simulation results show that MIMO radar has a better angular resolution than conventional phased array radar. The effectiveness of maximum likelihood estimator is also verified through the simulations.
Acknowledgements
This work is supported by National Nature Science Foundation of China (NSFC)
Figure 1. RMSE of DOA.
Figure 2. RMSE of initial velocity.
Figure 3. RMSE of acceleration.
under Grants 61471365, U1633107 and 61231017, National University’s Basic Research Foundation of China under Grant No. 2000300446. The work is also supported by the Foundation for Sky Young Scholars of Civil Aviation University of China.
Cite this paper
Li, H., Xu, L. and Zhang, Z. (2017) Parameter Estimation of Maneuvering Target Using Maximum Like- lihood Estimation for MIMO Radar with Colocated Antennas. Journal of Computer and Communications, 5, 69-74. https://doi.org/10.4236/jcc.2017.53008
References
- 1. Goldsmith, A., Jafar, S.A., Jindal, N. and Vishwanath, S. (2003) Capacity Limits of MIMO Channels. IEEE Journal on Selected Areas in Communications, 21, 684-702. https://doi.org/10.1109/JSAC.2003.810294
- 2. Cui, S.G., Goldsmith, A.J. and Bahai, A. (2004) Energy-Efficiency of MIMO and Cooperative MIMO Techniques in Sensor Networks. IEEE Journal on Selected Areas in Communications, 22, 1089-1098. https://doi.org/10.1109/JSAC.2004.830916
- 3. Li, J. and Stoica, P. (2007) MIMO Radar with Colocated Antennas. IEEE Signal Processing Magazine, 24, 106-114. https://doi.org/10.1109/MSP.2007.904812
- 4. Haimovich, A.M., Blum, R.S. and Cimini, L. (2008) MIMO Radar with Widely Separated Antennas. IEEE Signal Processing Magazine, 25, 116-129. https://doi.org/10.1109/MSP.2008.4408448
- 5. Dang, X.F., Ma, K., Chen, B.X. and Yang, M.L. (2016) Direction of Arrival Esti-mation for Monostatic MIMO Radar Using Reduced-dimension RISR Algorithm. 11th International Symposium on Antennas, Prop-agation and EM Theory (ISAPE), Guilin, China, 18-21 October 2016, 607-611.
- 6. Hokiguchi, M., Kikuma, N. and Sakakibara, K. (2016) Target Direction Estimation by MIMO Radar Using Root-MUSIC with Minimum Redundancy Array, International Symposium on Antennas and Propagation (ISAP), Okinawa, Japan, 24-28 October 2016, 1036-1037.
- 7. He, Q., Blum, R.S., Godrich, H. and Haimovich, A.M. (2010) Target Velocity Estimation and Antenna Placement for MIMO Radar with Widely Separated Antennas. IEEE Journal of Selected Topics in Signal Processing, 4, 79-100. https://doi.org/10.1109/JSTSP.2009.2038974
- 8. Jiang, M., Huang, J.G. and Hou, Y.S. (2010) MIMO Radar Joint Estimation of Target Location and Velocity with Multiple Subcarrier Signals. IEEE International Symposium on Phased Array Systems and Tech-nology. Boston, 12-15 October 2010, 398-402. https://doi.org/10.1109/ARRAY.2010.5613338
- 9. Sajjadieh, M.H.S. and Asif, A. (2015) Compressive Sensing Time Reversal MIMO Radar: Joint Direction and Doppler Frequency Estimation. IEEE Signal Processing Letters, 22, 1283-1287. https://doi.org/10.1109/LSP.2015.2396650
- 10. Wang, N., Wang, W.G., Zhang, F. and Yuan, Y.N. (2014) The PARAFAC-MUSIC Algorithm for DOA Estimation with Doppler Frequency in a MIMO Radar System. International Journal of Antennas and Propagation, 2014, 1-5. https://doi.org/10.1155/2014/684591




