Open Journal of Social Sciences
Vol.05 No.03(2017), Article ID:74648,11 pages
10.4236/jss.2017.53003
A Model of Competition between Online Lenders Offering Differing Loan Covenants
Erik Benrud
Finance Department, Peking University HSBC Business School, Shenzhen, China




Received: February 23, 2017; Accepted: March 6, 2017; Published: March 13, 2017
ABSTRACT
This paper develops a model where two online lenders compete with the interest rates charged and the severity of loan covenants imposed. The model has a stable equilibrium, which demonstrates how an increase in the number of online borrowers or an increase in the cost of meeting covenants by the borrowers will reduce the severity of the covenants required by lenders, and each of these changes will increase the difference in the severity of the loan covenant levels. An increase in the expected losses to the lender from relaxing covenants will increase the severity of loan covenants, and this will also make the levels of severity more dispersed. Additional analysis demonstrates how exogenous shifts affect the interest rates charged by the lenders and their profits.
Keywords:
Banking, Loan Covenants, Product Differentiation, Competition

1. Introduction
The purpose of this article is to introduce a model that describes the competition between online lenders who have flexibility in determining the rates charged and covenants imposed. The online lenders lower competition by differentiating themselves with these two choice variables. The lenders’ profit functions include the severity of loan covenants as an argument, which affects costs. The borrower’s profit function also includes a measure of the severity of loan covenants. The resulting model can help practitioners and researchers understand how online lenders who can offer varying terms in the loan contracts will choose the terms based upon the perceived risk of relaxing loan covenants, the number of borrowers, and borrowers’ costs of complying with a given level of severity of loan covenants. The results will help predict future trends in loan covenants and rates in the online lending market based upon the number and characteristics of borrowers.
The Internet provides a means for businesses to connect with customers and do transactions undreamed of a few decades ago. Buyers and sellers connect on EBay to negotiate prices. Travelers use online sites to find lodging in private homes. Borrowers can now search for lenders who will offer terms that best fit their needs, and online lenders must compete for that business. The online lending industry is particularly attractive to households and small businesses with diverse needs and higher risk than established corporate borrowers. Like any industry, businesses will find it beneficial to specialize. Some lenders will prefer to service more secure borrowers, impose more strict covenants that these borrowers are likely to meet, and charge a lower interest rate. Another group of lenders will charge higher interest rates to less secure borrowers who cannot meet strict covenants. Our model examines how lenders might differentiate themselves with respect to the interest rates charged and the severity of the loan covenants. The model contributes to the literature on bank competition that has grown substantially with the trends in deregulation and now the growth of the online lending. Early examples in this line of literature include [1] who model banks’ choices of geographical reach and loan pricing and [2] who examine the competition for deposits.
The model in this paper is an adaptation of a general model developed by [3]. That is now an established model in the industrial organization literature, and it describes a duopoly market where the firms avoid direct competition by offering products with different qualities and prices. We build upon that model by including three lenders that offer loans with different severity of loan covenants to avoid direct competition. There is one lender who offers only fully secured loans and two online lenders who offer loans with less severe covenants. The online lenders avoid direct competition by differentiating themselves with respect to the severity of the covenants they require and the interest rate they charge borrowers.
The model determines the market share, profits, and equilibrium severity of loan covenant (SLC) levels in terms of exogenous parameters such as the expected loss associated with a given level of SLC, the number of borrowers, the cost of borrowers to comply with the covenants, and macroeconomic risk. The model demonstrates that when the cost of complying with covenants increases (decreases), the SLCs will decrease (increase) and diverge (converge). When decreasing the severity of loan covenants has a larger (lower) impact on expected losses, however, the SLCs will increase (decrease) and diverge (converge).
The review of the literature in the next section provides the sources of the theories and assumptions used in this model. After that section, we introduce the parameters within the framework of a market where there is one lender who only makes fully secured loans and an online lender who offers loans with less severe covenants at a higher interest rate. After that, we expand the model to include a second online lender who offers loans with less severe covenants. Then, there is a section that employs comparative statics to demonstrate the implications of the model, which is followed by summary and discussion.
2. Review of the Literature
Models analyzing the effects of quality competition are important because a larger variety of products available to consumers improves economic welfare, see [3] and [4]. Furthermore, new entrants will always try to find their own market niche, e.g., lending to small businesses online, and that niche may be defined in terms of quality. Previous researchers have verified how it is often too costly for monopolists offering a given quality of goods to prevent entrants with a different quality product from entering the market; see [5], [6] and [7]. This section summarizes the development of the economic and finance literature that explores the dynamics and effects of this competitive process.
Over the years, a large literature has built upon early works such as [8] and [9] to show how quality differentiation relaxes price competition. The reason for such differentiation is to avoid the [10] outcome associated with firms that compete with the same quality product. Researchers have created the moniker “Bertrand death” to describe a competitive situation where prices are falling and production costs are increasing. In the resulting equilibrium, the firms have non-positive profits, see [3]. According to [11], “loss-making strategies will be avoided” by firms; also, “if a profitable opportunity exists in the market, there is ‘one smart agent’ who will fill it.” Rather than risking a competitive outcome where profits are non-positive, the entering firm can choose a quality that is different enough to allow it to not directly compete with the existing firm.
There is a lengthy literature on the entry of firms into industries where profit opportunities exist. The work in [12] and [13] pioneered the modern sequential-entry models. The work in [14] extended the model to allow for endogenous prices, and this development has characterized later models including the one in this paper. Subsequent work in this area includes [3], [9], [15]-[21]. The model here builds upon the model established in [3]. The model in [3] is a vertical differentiation model with a stable and tractable equilibrium. Furthermore, the consumer utility function of the model in [3] easily adapts to a profit function of a borrowers who pay an interest rate and must incur a cost to comply with loan covenants.
As [11] mentions, there is usually not one “true model” to describe a given market. Several models may apply. This paper lays a solid foundation for future work in this area by thoroughly investigating the results associated with the modification of an established spatial model in the industrial organizations literature. In our model, the second-order conditions are satisfied, and the model yields a unique and stable equilibrium. Having successfully adapted one model from the industrial organizations literature to the market for online loans with lower levels of the severity of loan covenants compared to traditional banks, future research can explore the extent to which other models apply.
The next section summarizes the assumptions of the model in [3], modifies that model so that its inputs correspond to parameters in the market for borrowed funds. That section lays the groundwork for the sections that describe an online duopoly lending market characterized by vertical product differentiation and how covenant severity levels and interest rates react to changes in exogenous parameters
3. A Model of a Single Online Lender Market
This section serves two purposes. It introduces the parameters of the market and the corresponding simplifying assumptions of the model. It also describes the model’s equilibrium with only one online lender offering loans with a low SLC at a higher interest rate. There is also a lender who only makes loans with an SLC sufficiently high so as to make the loans fully secured. The equilibrium is a standard result, but it sets the stage for examining the results when there are two online lenders competing for loans that are not fully secured.
As mentioned earlier, our model builds upon the model in [3], which only has two firms competing with quality. In our full model, borrowers have three choices. The first choice is to choose to borrow from a traditional bank. This means the borrowers must meet some high level of SLC, which make the loans fully secured and pay a low interest rate. The other two choices consist of two lenders who offer lower but distinct SLCs and correspondingly higher interest rates. Before introducing that three-lender market, we first consider a case where there is only one online lender with a low SLC compared to traditional banks.
To describe how the borrowers make their choices, we adapt the indirect utility function of consumers used by [3]. The indirect utility function in the model in [3] has income, price, taste and quality which are represented by y, Pi, θ, and qi, respectively:
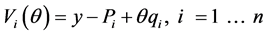 (1)
(1)
Each period, consumers purchase and consume a single unit of the product indexed i. The price and quality of the product are Pi and qi, respectively. The increase in utility from consuming the product depends on each agent’s unique preference factor denoted θ. Preferences follow a uniform distribution over an interval bounded by a lower and upper value of θ. The quality levels have this relationship: qL < qH. The symbol qH represents the quality level offered by the high-quality producer or the monopolist in the single-seller case. In the duopoly market, the low-quality producer offers qL. The net benefit of consuming product variety i is given by the quantity θqi − Pi. Using the same basic concept, we propose the following profit function of the borrower:
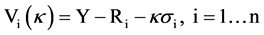 (2)
(2)
where:
Y: the level of return expected from investing the proceeds of the loan,
Ri: the interest rate charged on the loan,
κ: the covenant cost factor that determines the cost of complying with a given SLC,
σi: the severity of the covenants or SLC.
Each borrower takes the same size loan and invests the proceeds in an endeavor that will produce a positive return, Y, either in the form of direct profit in the case of a business loan or the elimination of rental payments and capital gains in the case of a home loan. The interest rate consists of two portions: Ri = r0 + ri. The term r0 is the rate charged on a loan where the SLC is high enough to make the loan essentially free of loan specific, i.e., idiosyncratic, risk; therefore, for loans with an SLC = σ0 so there is no idiosyncratic risk R0 = r0. The term ri is a premium charged by the lender for imposing a lower SLC σi < σ0, where σi represents the SLC where idiosyncratic risk is positive. We assume that that R0, the interest rate for loans without idiosyncratic risk, is exogenously determined.
The borrowers choose a particular interest rate and SLC to maximize profits given the costs they incur from meeting the SLC, which depends upon the borrower’s cost factor κ. In a case where there is just one online lender, the borrowers have the choice between σ0 and paying the basic rate R0 and paying the higher R1 for the lower σ1. Borrowers characterized by κ > r1/(σ0 − σ1) = κ* will choose to pay R1 for only facing σ1. In other words, borrowers with a higher value of κ are willing to pay the higher interest rate to reduce the SLC.
As assumed in the ADT model and many other models of this type, κ is uniformly distributed and identifies each borrower. The lower bound on κ is zero, and there is an upper bound, which we denote K. The value of the density function over zero to K is the number of potential borrowers divided by the upper limit of the covenant cost factor. Letting N represent the number of borrowers and ϕ’(κ) represent the density function, we can write ϕ’(κ) = N/K when 0 ≤ κ ≤ K, else ϕ’(κ) = 0. At this point we assume that Y is sufficiently high so as to exceed both the interest rate and the costs of adhering to the loan covenants. Future research will examine the implications of the possibility of Y < Ri + κσi.
Lenders face an expected cost loss function based upon the severity of the covenants1:
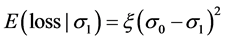
For the lender that makes loans with σ0, the expected loss is negligible. The low SLC lender will incur higher expected losses by lowering the SLC by the distance given by (σ0 − σ1). There is a scale factor ξ that varies with the state of the economy, and there is an increasing expected loss from each unit increase in (σ0 − σ1). The profit functions are:
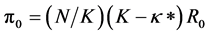 (3.a)
(3.a)
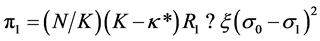 (3.b)
(3.b)
The interest rate and SLC and, hence, the profit for the lender making loans with the SLC associated with σ0 are exogenously determined by the economy. Thus, the lender offering loans with the SLC = σ1 makes a choice of the interest rate to charge and the value of σ1. Substituting κ* into the profit function of that lender and optimizing with respect to the interest rate gives this expression for the optimal rate: R1* = r0 + K(σ0 − σ1)/2. Using the assumed distribution ofκ gives the following expression: κ* = [K(σ0 − σ1)/2]/(σ0 − σ1) = K/2. This is a standard result in a market where only one firm makes price and quality or quantity decisions. It is immutable with respect to the choices of interest rate and SLC and the lender’s expected loss function2.
Exogenous parameters determine the values for R1, π1 and σ1. The first-order conditions provide the solution for the optimal σ1. The online lender is willing to lower the SLC below σ0 by the amount: σ0 − σ1= 0.125NK/ξ. This expression can be rearranged to give the solution for the optimal σ1
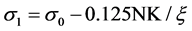 (4)
(4)
Other things equal, a unit increase/decrease in σ0 will increase/decrease σ1 by an equal amount. The absolute difference in SLCs increases when N or K increases. Naturally, the online lender finds it profitable to accommodate an increase in the costs of borrowers to meet loan covenants by distinguishing its product more from σ0. Likewise, since dσ1/dξ = 0.125NK/ξ2 > 0, the lender will increase SLC when the expected loss parameter ξincreases. Since the low-SLC lender will always lend to K/2 investors, an increase in K motivates the lender to lower the SLC. An increase in N increases the marginal revenue from a given increase in R1, and the lender will lower σ1.
The interest rate is R1 = r0 + 0.0625NK2/ξ. The profit of the online lender is π1 = 0.015625(NK)2/ξ, and dπ1/dK > 0, dπ1/dN > 0, dπ1/dξ < 0. A higher cost of meeting loan covenants and a larger population of borrowers increase profits. An increase in the expected loss from a given lowering of the LCS lowers profits.
These results hold when κ follows a distribution other than the uniform distribution. A cumulative distribution function, denoted ϕ(κ), allows for a more general expression:
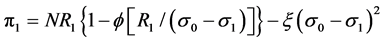 (5)
(5)
Optimal fee, given κ*, is R1* = r0 + [1 − ϕ(κ*)]/[(σ0 − σ1) − ϕ'(κ*)], which then gives the expression: κ* = [1 − ϕ(κ*)]/ϕ'(κ*). The value of κ* is a constant nominal value for many distributions. Unique solutions exist for κ* and the second-order conditions are satisfied when ϕ(κ) represents a uniform, normal or exponential distribution3.
The results developed in this section are straightforward and conform to intuition. The goal of this section has been to demonstrate the results of the model in the relatively simple case of a single lender that can choose its level of SLC and interest rate competing with a lender who can only make loans free of idiosyncratic risk with an exogenously determined SLC. The next section investigates the results when a second lower SLC lender enters the market offering borrowers more choices of SLC and interest rate combinations.
4. Competition between Two Online Lenders
To describe the interaction of the lower and lowest SLCs, i.e., the competing online lenders, we use the widely used assumption that lenders engage in a quality-then-price two-stage game. In this case the lenders choose the SLC level, i.e., σi, first then the interest rate. Representative work in this area includes [3], [22], [23] and [24]. The model developed here has a stable equilibrium that defines the market share, interest rates, SLC levels, and profits of the lenders in terms of the external parameters defined in the previous section.
In the first stage of the game, the online lenders recognize how their choices of σi determine market shares. The two online lenders offer distinct SLC levels as characterized by σ1 > σ2and R1 < R2. Henceforth, the terms “lender 1” and “lender 2” refer to the higher and lower covenant severity levels respectively4. Recalling expression (2), the condition that leads a borrower to choose the higher SLC of the two lower SLC lenders is −R1 − κσ1> −R2 − κσ2. The preference factors for the marginal borrowers are:
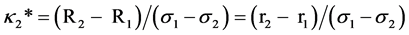 (6.a)
(6.a)
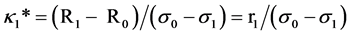 (6.b)
(6.b)
The term (N/K)(K − κ2*) indicates the number of online borrowers who take out loans with the lowest SLC from lender 2. The corresponding measure for lender 1 is (N/K)(κ2* − κ1*). Solving for each Ri* as before yields,
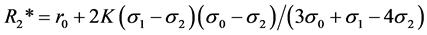 (7.a)
(7.a)
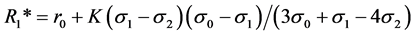 (7.b)
(7.b)
For ease of notation we write R2* = r0 + 2Kδ1,2δ0,2/ω and R1* = r0 + Kδ0,1δ1,2/ω. The implied transformations are δ0,2 = σ0 − σ2, δ0,1 = σ0 − σ1, δ1,2 = σ1 − σ2, ω = 3σ0 + σ1 − 4σ2.
The profit functions in the first stage of the game are:
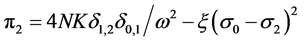 (8.a)
(8.a)
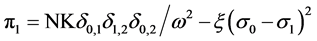 (8.b)
(8.b)
The first-order conditions for lenders 2 and 1 respectively are5,
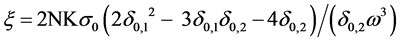 (9.a)
(9.a)
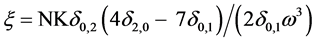 (9.b)
(9.b)
Equating the two expressions for ξ gives a third degree polynomial in a variable defined as δ0,2/δ0,1. Only a single real root exists: δ0,2/δ0,1 = 5.25123. Entering this value into the equations above yields solutions for the relaxation of the respective SLCs is:
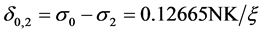 (10.a)
(10.a)
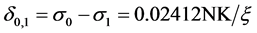 (10.b)
(10.b)
These expressions define several interesting relationships. Using the term NK/ξ as a unit of measure, for example, lender 1 relaxes the SLC from σ0 to σ1, but that distance is less than one fifth the distance of σ0 − σ2. If both online lenders offer the optimal SLCs, their market shares are invariant in this model.
The interest rates are R2 = r0 + 0.05383NK2/ξ and R1 = r0 + 0.00513NK2/ξ. Profits per period are π2 = 0.0122193(NK)2/ξ and π1 = 0.0005075(NK)2/ξ. We note that lender 2 earns the higher profit, which is consistent with [25] that posits the higher-quality firm will earn the higher profits, but this depends upon our assumption that Y > Ri + κσi for all the lenders, i.e., the lender’s interest rate and the SLC are not so high to eliminate some possible borrowers with high values of κ.
The competition forces interest rates on the online loans to decline. The rate R2 in the three lender case is about 14% lower than R1 in the case where there was only the lender who makes fully secured loans and a single low-SLC or online lender. The corresponding SLC declines by about one percent. These adjustments increase that online lender’s market share from 50% to 52.5%. Lender 2 serves 26.25% of all potential online borrowers. The remaining 21.25% borrowers choose R0 and σ0. These market shares are immutable as long as all lenders remain in the market and ξ is the same for both low SLC lenders.
This section has developed the basic vertical differentiation model in a duopoly market for online lenders offering varying levels of SLC below the fixed level of traditional banks. The model builds upon that proposed by ADT by offering the borrowers three choices and by redefining the parameters so the model can apply to competition between online lenders. Under these conditions, an equilibrium exists that is characterized by a unique set of SLCs, interest rates, profits and market shares. The next section examines how changes in exogenous parameters affect that equilibrium.
5. How Exogenous Shifts Affect Severity of Loan Covenants and Interest Rates
This section examines how changes in exogenous parameters affect the equilibrium derived in the previous section. Comparative statics yield interesting results with respect to how the equilibrium SLC levels, interest rates and profits react to changes in σ0, ξ, N and K. Respectively, these parameters relate to the severity of loan covenants needed to reduce idiosyncratic risk, a scale parameter for the expected losses from lowering the SLC, the number of borrowers, and the costs the borrowers incur from complying with the covenants.
The comparative statics reveal the conditions that lead to changes in the level and distribution of the SLCs offered by the online lenders offering lower SLCs compared to traditional banks. The results in the previous sections yield the following expressions for quality levels: σ2 = σ0 − 0.12665NK/ξ and σ1 = σ0 − 0.02412NK/ξ. The distance between the SLC levels is σ1 − σ2 = 0.10253NK/ξ. Thus, when σ0 changes, both lower SLC levels change an equal amount. An increase in σ0 would correspond to a more risky environment as the level of SLC to eliminate idiosyncratic risk increases. Macroeconomic variables would determine the value of σ0.
Lender 2’s SLC is more sensitive to changes in the distribution of the borrower’s cost factor:
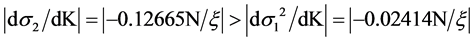 (11)
(11)
Given a fixed number of potential borrowers, an increase in K implies that the borrowers incur higher costs for complying with the loan covenants. The equilibrium conditions imply that an increase in K will decrease the SLC, profit and interest rate more for lender 2 than for lender 1. The choice variables for lender 1 are less responsive because lender 0 offers the immutable choice of R0 and σ0. If K falls, the lenders will allow σ2and σ1 to increase, but lender 1 cannot allow σ1 to increase too much because σ0 does not change. In summary, an increase (decrease) in K decreases (increases) both s1 and s2, the quantity s1-s2 increases (decreases), interest rates diverge (converge) and profits diverge (converge).
Since the term (NK) appears in the expressions for interest rates, profits, and SLCs, it should be obvious that an increase in the number of borrowers will affect the equilibrium in basically the same way as an increase in K. With a larger number of borrowers in each of their market shares, lenders find that they can increase profits by decreasing the SLCs and the interest rate.
The SLCs offered by lender 1 and lender 2 will converge in reaction to an increase in ξ:
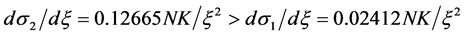
but d(σ1 − σ2)/dξ = −0.10253NK/ξ2. The reason for the convergence of SLCs in response to an increase in the cost factor is that lender 1 cannot allow its SLC to get too that of traditional banks. Nevertheless, since lender 2 has much higher expected losses, the scale factor for costs will have a much larger effect on lender 2’s profits and interest rates. Compared to lender 1, the increase in ξ will lower the profits and interest rates of lender 2 more in absolute terms. In summary, with respect to the SLCs, an increase (decrease) in ξ will increase (decrease) both σ1 and σ2, and the quantity σ1 − σ2 decreases (increases). An increase (decrease) in ξ will decrease (increase) profits and the absolute difference between the profit levels will decrease. Interestingly enough, an increase (decrease) in ξ will decrease (increase) interest rates as the online lenders increase the SLCs, and the absolute difference between the interest rates will decrease.
In all cases, when an exogenous shift increases (decreases) interest rates, the absolute difference between the interest rates increases (decreases). The same is true for profits. The more interesting result is how the difference in the SLCs depends on exogenous parameters. Although the SLC levels move in the same direction in reaction to a change in a given exogenous variable, whether the SLC levels diverge or converge depends on which exogenous variable brought about the change. Whether these relationships are realistic is the subject of future research as discussed in the next section.
6. Discussion
This paper demonstrates a methodology for analyzing how online lenders willing to make loans to households and small businesses can compete with different levels of severity of loan covenants (SLCs). Future research can build on this model, which describes the relationship between a two online lenders, i.e., lenders who offer different levels of lower SLCs. Previous research supports the proposition that a second firm can enter the market if it chooses to produce a product of a different quality, and the existence of a variety of qualities in various financial products, e.g., brokerage services and trading platform accuracy and now online lending, supports this proposition. Our model demonstrates how the market forces determine interest rates, SLC levels, and profits in a market where there are three lenders of which two choose to offer the lower SLC loans.
As market forces change, the SLC levels offered by each lender will change but by different amounts. Future empirical research can test the relevancy of the model’s outcomes such as the relative sensitivities of the interest rates and SLC levels. Future research can also explore how the competition also lowers industry profits, which should increase social welfare.
These results provide a foundation for both theoretical and empirical research. Future work will relax assumptions concerning the distribution of the covenant cost factor and allow the return, Y, the borrowers plan to earn on their investment to vary across investors and even fall below a range of values Ri + kσi, where k < K. Although game-theory models can become very complex, continued work in this field will allow researchers and practitioners to better understand the evolving market for financial services such as the market for loans with different severity of loan covenants.
Cite this paper
Benrud, E. (2017) A Model of Competition between Online Lenders Offering Differing Loan Covenants. Open Journal of Social Sciences, 5, 16-26. https://doi.org/10.4236/jss.2017.53003
References
- 1. Anderson, S., de Palma, A. and Thisse, J. (1992) Discrete Choice Theory of Product Differentiation. MIT Press, Cam-bridge.
- 2. Benoit, J. and Krishna, V. (1987) Dynamic Duopoly: Prices and Quantities. Review of Economic Studies, 54, 23-35. https://doi.org/10.2307/2297443
- 3. Bertrand, J. (1883) Review of “Theorie mathematique de la richesse sociale” and “Recherche sur les principes mathematiques de la theorie des richesses”. Journal des Savants, 499-508.
- 4. Degryse, H. (1996) On the Interaction between Vertical and Horizontal Product Differentiation: An Application to Banking. The Journal of Industrial Economics, 44, 169-187. https://doi.org/10.2307/2950644
- 5. Dewatripont, M. (1987) The Role of Indifference in Sequential Models of Spatial Competition. Economics Letters, 23, 323-328. https://doi.org/10.1016/0165-1765(87)90138-8
- 6. Dixit, A. (1980) The Role of Investment in Entry Deterrence. Economic Journal, 90, 95-106. https://doi.org/10.2307/2231658
- 7. Donnenfeld, S. and Shlomo, W. (1992) Vertical Product Differentiation with Entry. International Journal of Industrial Organization, 10, 449-472. https://doi.org/10.1016/0167-7187(92)90007-L
- 8. Eaton, B. and Ware, R. (1987) A Theory of Market Structure with Sequential Entry. The Rand Journal of Economics, 18, 1-16. https://doi.org/10.2307/2555531
- 9. Harris, C. (1985) Existence and Characteri-zation of Perfect Equilibrium in Games of Perfect Information. Econometrica, 53, 613-616. https://doi.org/10.2307/1911658
- 10. Hay, D. (1976) Sequential Entry and Entry-Deterring Strategies in Spatial Competition. Oxford Economic Papers, 28, 220-257. https://doi.org/10.1093/oxfordjournals.oep.a041343
- 11. Jehiel, P. (1992) Product Differentiation and Price Collusion. International Journal of Industrial Organization, 10, 1633-1641. https://doi.org/10.1016/0167-7187(92)90063-5
- 12. Lane, W. (1980) Product Differentiation in a Market with Sequential Entry. Bell Journal of Economics, 11, 237-260. https://doi.org/10.2307/3003410
- 13. Lehmann-Grube, U. (1997) Strategic Choice of Quality When Quality is Costly: The Persistence of the High-Quality Advantage. RAND Journal of Economics, 28, 372- 384. https://doi.org/10.2307/2555811
- 14. Leland, H. (1977) Quality Choice and Competition. American Economic Review, 67, 127-138.
- 15. Matutes, C. and Padilla, A. (1994) Shared ATM Networks and Banking Competition. European Economic Review, 38, 1113-1138. https://doi.org/10.1016/0014-2921(94)90040-X
- 16. Mclean, R. and Riordan, M. (1989) Industry Structure with Sequential Tech-nological Choice. Journal of Economic Theory, 47, 1-21. https://doi.org/10.1016/0022-0531(89)90099-9
- 17. Mussa, M. and Sherwin, R. (1978) Monopoly and Product Quality. Journal of Economic Theory, 18, 301-317. https://doi.org/10.1016/0022-0531(78)90085-6
- 18. Prescott, E. and Visscher, M. (1977) Sequential Location among Firms with Foresight. Bell Journal of Economics, 8, 378-393. https://doi.org/10.2307/3003293
- 19. Schwartz, M. and Baumann, M. (1988) Entry-Deterrence Externalities and Relative Firm Size. International Journal of Industrial Organization, 6, 181-197. https://doi.org/10.1016/S0167-7187(88)80024-9
- 20. Schwartz, M. and Thompson, E. (1986) Divisionalization and Entry Deterrence. Quarterly Journal of Economics, 101, 307-321. https://doi.org/10.2307/1891117
- 21. Shaked, A. and Sutton, J. (1982) Relaxing Price Competition through Product Differentiation. Review of Economic Studies, 49, 3-14. https://doi.org/10.2307/2297136
- 22. Sutton, J. (1997) One Smart Agent. RAND Journal of Economics, 28, 605-628. https://doi.org/10.2307/2555778
- 23. Tirole, J. (1988) The Theory of Industrial Organization. MIT Press, Cambridge.
- 24. Vives, X. (1988) Sequential Entry, Industry Structure and Welfare. European Economic Review, 32, 1671-1687. https://doi.org/10.1016/0014-2921(88)90025-6
- 25. Xavier, W. (1996) Quality Choice in Models of Vertical Differentiation. The Journal of Industrial Economics, 44, 345-353. https://doi.org/10.2307/2950501
NOTES
1The cost function can also be interpreted as being determined by the number of loans made since the distance (σ0 − σ1) also determines the number of loans the low SLC lender makes.
2The first derivative is dπ1/dσ1 = −(R2/4) + 2ξ(σ0 − σ1). The second-order condition is satisfied: d2p1/d(σ1)2 = −2ξ.
3There are distributions for which k* is not unique. One example is ϕ(κ) = 1 − K/κ; κ: [C, + 4), where C is a positive constant.
4We should note that the “lender 1” may not be the incumbent. In other words, when the second lender tries to enter, the incumbent may position itself to offer σ2 and R2.
5The first-order conditions yield reaction functions in the plane defined by σ1 and σ2. The first order conditions give: σ2 = 5.25123σ1 − 4.25123σ0; therefore when an equilibrium combination of σ2 and σ1 exists, it is unique. The second-order conditions are satisfied: d2π2/dσ22 = −8NK(δ0,1 + 5δ0,2)δ0,12/ω4 < 0 and d2π1/dσ12 = −2NK(7δ0,1 + 8δ2,0)δ2,02/ω4 < 0.