Open Journal of Safety Science and Technology, 2011, 1, 31-42
doi:10.4236/ojsst.2011.12004 Published Online September 2011 (http://www.SciRP.org/journal/ojsst)
Blast Wave Parameters for Spherical Explosives
Detonation in Free Air
I. Sochet1, D. Gardebas2, S. Calderara2, Y. Marchal2, B. Longuet3
1Ecole Nationale Supérieu re d’Ingénieurs de Bourges , Institut PRISME, Bourges, France
2Institut de Recherche Criminelle de la Gendarmerie Nationale (IRCGN),
Division Criminalistique Physique et Chimie,
Rosny-sous-Bois, France
3 Direction Générale de l’Armement (DGA) Techniques Terrestres, Bourges, France
Received May 24, 2011; revised July 19, 2011; accepted July 25, 2011
Abstract
Several formulations have been published to define the characteristic parameters of an incident blast wave.
In almost all previous work, the charge examined has been TNT explosive and overpressure has been the
main parameter examined. In this paper, we describe an investigation based on three explosives, TNT, PETN
and ANFO, which has been conducted by considering three parameters: overpressure, duration and impulse
of the positive blast wave phase. Calculations of the three parameters were conducted using TM5-855
through the tool CONWEP and AUTODYN. The positive overpressures were calculated using the new fo-
rensic software ASIDE. The evolution of these blast wave parameters is expressed by combining the laws of
two approaches: the forensic approach and the security approach. TNT equivalents are expressed in terms of
pressure and impulse for the comparisons of ANFO and PETN.
Keywords: ANFO, Blast Wave, Duration, Explosive, Impulse, Overpressure, PETN, TNT
1. Introduction
To protect property and persons working on sites that
handle, store or transport large quantities of flammable
materials, it is necessary to estimate the effects of pres-
sure resulting from an explosion, whether the explosion
occurs at a close or a distant location. In this work, we
consider explosions that are caused by pyrotechnic
charges, whether intentional or accidental. Applications
of pyrotechnic materials cover a variety of areas, includ-
ing satellite technology, tactical and ballistic missiles,
ammunitions, law enforcement, security, space launch
vehicles, aerospace, automotive safety (airbags), railway
signal devices and charges for the oil industry, demoli-
tion mines, quarries and buildings.
The objective of this work is to establish relationships
to evaluate the mechanical effects of shock waves in free
fields. We propose a dual approach using both forensic
and security analyses. The forensic analysis uses obser-
vations of damage occurring at varying distances from
the blast site to estimate the pressure and deduce the
corresponding mass equivalent of TNT. The security
approach, on the other hand, assumes that the mass of
products stored or the equivalent TNT charge is known,
such that the range of the resulting pressure, and there-
fore the resultant damage, must be determined.
This study was conducted for three explosives: TriNi-
troToluene (TNT), PEntaerythritol TetraNitrate (PETN)
and Ammonium Nitrate/Fuel Oil (ANFO). TNT is a
chemical compound that consists of an aromatic hydro-
carbon crystal. In its refined form, TNT is relatively sta-
ble and is not sensitive to shock or friction. TNT is one
of the most commonly used military and industrial ex-
plosives and is often used as a reference explosive.
PETN is one of the most powerful explosives known. It
is more sensitive to shock, friction and electrostatic dis-
charge than TNT. It is mainly used as principal com-
pound in some military explosives compositions (plas-
trite, semtex…), in detonators. In medicine, PETN is
used as a vasodilator. ANFO is a highly explosive mix-
ture consisting of ammonium nitrate and diesel fuel. The
diesel fuel can be replaced by kerosene, gasoline or bio-
fuels, but the cost and low volatility of diesel makes it
ideal. Ammonium nitrate is water-soluble and very hy-

I. SOCHET ET AL. 32
groscopic, i.e., it readily absorbs water from the air. This
absorption interferes with its ability to explode, and it
must therefore be stored in a dry location. The popularity
of ANFO is largely based on its low cost and high stabil-
ity. Because of its relative ease of manufacture, its low
cost compared to other types of similar explosives and
the stability of its two components, ANFO has been used
in several terrorist attacks (1970, University of Wiscon-
sin-Madison; 1995, Oklahoma City).
of CO2, H2O and N2, respectively. The term oxygen
balance (OB) represents the concentration of oxygen
atoms in an oxidant and indicates its oxidation potential.
It expresses the number of molecules of oxygen remain-
ing after the oxidation of H, C, Mg, and Al into H2O,
CO2, MgO2 and Al2O3, respectively. The oxygen balance
can be expressed more directly for a conventional explo-
sive by the following equation:
abcd
CHNO
In this study, we will first explore the thermochemical
data on these explosives and then analyze the effects of
blast waves.
2. Thermodynamics of Explosions



1600d2ab 2
OB MWexp losive

 (1)
where MW is the molecular weight. In this equation, the
factor 1600 is the product of the molecular weight of
oxygen expressed as a percentage (MW (O) × 100%).
The OB provides information about the products that
are formed in the reaction. A positive value indicates an
excess of oxygen in the explosive, whereas a negative
value indicates oxygen levels that are insufficient to ob-
tain a complete oxidation reaction. If the oxygen balance
is strongly negative, there is not enough oxygen to form
CO2, and toxic gases such as CO are formed instead.
Note that the oxygen balance provides no information
about the exchange of energy during the explosion.
The explosives studied here highlight the difficulty in
choosing an appropriate value for detonation energy.
“Heat of detonation” is defined as the heat of the reac-
tion of the explosive that results in the detonation prod-
ucts. This heat does not include the heat generated by
secondary reactions of the explosive or its products with
air. There is some confusion in terminology related to
detonation energy and heat of detonation, and the two are
often used interchangeably. The heat of detonation is
determined using calorimetric methods in a closed
chamber and does not take into account the energy
available from the highly compressed gases in the prod-
ucts, which can significantly contribute to the energy
transmitted by a blast wave, as outlined in Scilly [1].
Therefore, the term “detonation energy” will hereafter be
devoted to the calculated energy of the detonation of an
explosive without considering the presence of air. De-
termination of the detonation energy is therefore based
on prior knowledge of the decomposition of the explo-
sive, which itself depends on the oxygen balance.
Therefore, we will examine the oxygen balance of each
of the explosives under consideration, as well as their
decomposition-based models.
Calculation of the oxygen balance of TNT and PETN
is relatively simple because the chemical formulas of
these materials are distinctly defined. However, this is
not the case for ANFO, which is a mixture of ammonium
nitrate (AN) and fuel oils (FO) in a ratio of 94:6 AN:FO.
Table 1 indicates that TNT has the highest oxygen
deficit and that ANFO, PETN do not have sufficient
oxygen to obtain complete oxidation reactions and form
H2O and CO2. Hence, large amount of toxic gases like
carbon monoxide will be present. In case of ANFO, the
oxygen balance approaches zero. It means that the sensi-
tivity, strength and brisance of ANFO tend to the maxi-
mum.
2.2. Decomposition Rules
2.1. Oxygen Balance To clarify the formation of decomposition products [2], a
set of rules, known as the “Kistiakowsky-Wilson” rules
(K-W rules), has been developed. The rules are used for
explosives with moderate oxygen deficits and an oxygen
balance greater than −40% and can be described as fol-
The detonation of an explosive is an oxidative reaction
that is based on the assumption that the available carbon,
hydrogen and nitrogen are used solely for the formation
Table 1. The oxygen balance of TNT, PETN and ANFO.
Name Chemical Formulation MW (g·mol−1) OB (%)
2,4,6-Trinitrotoluene (TNT) C7H5N3O6 227 −74
Pentaerythritol Tetranitrate or Pentrite (PETN) C5H8N4O12 316 −10.1
C0.365H4.713N2O3 [3,4] 85.1 −1.6
Ammonium Nitrate/ Fuel Oil (ANFO)
C0.336H4.656N2O3 [5] 84.7 0

I. SOCHET ET AL. 33
2.3. Detonation Energy lows:
1) First, the carbon atoms are converted into CO.
2) If oxygen remains, then hydrogen is oxidized into
water.
The explosives studied here highlight the complexity that
exists in identifying the correct value of detonation en-
ergy, i.e., whether the value should be chosen from the
literature or if it should be calculated. Generally, a ratio
of 1.5 exists between the minimum and maximum values,
depending on whether the values are obtained from ex-
periments or calculated and whether water is considered
a liquid or a gas reaction products. Moreover, the com-
position of products in an actual detonation is not always
the same for a given explosive. Factors such as density,
temperature, initial degree of confinement, particle size
and morphology and the size and shape of the load affect
the pressure and temperature behind the detonation front,
where the products undergo rapid expansion that is not
always balanced.
3) If oxygen still remains, then CO is oxidized to CO2.
4) All of the nitrogen is converted to N2.
For explosives with a lower OB, the modified K-W
rules are used. The modified rules are as follows:
1) The hydrogen atoms are converted into water.
2) If oxygen remains, then carbon is converted into
CO.
3) If oxygen still remains, then CO is oxidized to CO2.
4) All of the nitrogen is converted to N2.
The Springall-Roberts rules (S-R rules), which are de-
scribed below, add two additional conditions to the K-W
rules:
5) One-third of the CO formed is converted into car-
bon and CO2. The detonation energy can be calculated either from
the Helmholtz free energy [7] or from the reaction en-
thalpy. In the first case, the detonation energy is the en-
ergy transmitted by the explosive shock wave and is as-
sociated with the work done in the expansion of gases
produced during the explosion, which is described by
6) One-sixth of the original amount of CO is converted
to carbon and into water with the addition of hydrogen.
According to Scilly [1], the decomposition equation
recommended by Kamlet and Jacob (the K-J rule) can be
obtained as follows:


 
abcd
2
22
C HN O0.5d0.25bC
0.5d0.25bCO
0.5bHO0.5cN
a 

 
(2)
final
initial PV

 . By applying the first and second laws of ther-
modynamics, the change in the Helmholtz free energy
can be used to calculate the energy of explosion ex-
pressed in terms of internal energy and entropy
U
S

as follows:
In this scheme, CO is not formed preferentially and
CO2 is the only oxidation product of carbon. In addition,
H2O is always formed at the beginning of the reaction.
Kinney [6] considers that all of the oxygen is incorpo-
rated into carbon monoxide, which implies the following
chemical equation in the case of TNT:
75362 2
CHNOC 6CO 2.5H1.5N  (3)
Table 2 below summarizes the products formed by
each of the explosives considering the different rules of
decomposition.
F
UT S

 , where UHRTn
and ; ;
p
rpr pr
H
HHnnnSSS

(4)
Here subscripts p and r represents respectively the
products and the reactive.
In the second case, the reaction energy can be calcu-
lated by the enthalpy change involved in the chemical
reaction between the standard state products and reac-
tive.
Table 2. Decomposition of TNT, PETN and ANFO.
Products (mole number)
Explosive Rule
C CO CO2 H
2 H 2O N2
K-W 3.5 3.5 0 0 2.5 1.5
S-R 3 3 1 1.5 1 1.5
C7H5N3O6
K-J 5.25 0 1.75 0 2.5 1.5
K-W 0 2 3 0 4 2
C5H8N4O12
S-R or K-J 1 0 4 0 4 2
C0.365H4.713N2O3 S-R or K-J 0.043 0 0.322 0 2.356 1
C0.336H4.656N2O3 S-R or K-J 0 0 0.336 0 2.328 1

I. SOCHET ET AL. 34
Thus, calculation of the detonation energy was con-
ducted for different patterns of decomposition in TNT
and PETN by considering 1) water molecules in the
gaseous and liquid states, and 2) the data available in the
literature for enthalpies and entropies of formation of
explosives and detonation products. Only the enthalpies
and entropies of formation for TNT and PETN are re-
ported in Table 3 below.
The results of the calculations for each configuration
show that the detonation energy calculated using the free
energy is higher than that obtained using the reaction
enthalpy regardless of the explosive studied, and both of
these calculations are higher than the average value in
the literature. Moreover, the energies are greater if water
is considered in the liquid phase. However, regardless of
the enthalpy of formation selected, the results are always
in the same energy range for a given decomposition rule.
Tongchang et al. [8] have conducted experimental de-
terminations for TNT using a calorimeter in which the
cylindrical bomb had an internal volume of 5 L and
could support a pressure of 200 MPa. The experiments
were performed on maximum loads of 50 g. The explo-
sive force was measured as a function of the nature of the
cartridge (porcelain, brass) and its thickness. All tests
resulted in a value between −4.31 MJ·kg−1 and −4.40
MJ·kg−1 Finally, it should be emphasized that these val-
ues correlate with the values used by Gelfand (−4.517
MJ·kg−1) [9], Baker (−4.520 MJ·kg−1) [10], Pförtner
(−4.686 MJ·kg−1) [11] and Lannoy (−4.690 MJ·kg−1) [3],
in addition to the value proposed by Trelat [12] (−4.600
MJ·kg−1) that was obtained using the average of the
Baker [10] and Lannoy [3] results. Other detonation en-
ergy values are quoted by Filler [4], including the energy
calculated in the Encyclopedia of Chemical Technology
(−3.87 MJ·kg−1) [4], the measurement results from To-
negutti [4] that assume a 2 g charge with a conventional
calorimeter (detonation energy −3.21 MJ·kg−1) and the
measurements by the Armaments Research Establish-
ment for a load of 100 g (−4.535 MJ·kg−1). Omang et al.
[13] used a detonation energy value of −4.26 MJ kg−1 to
characterize the propagation of shock waves following
detonation of a spherical and hemispherical charge of 1
kg TNT. Thus, all energies of detonation reported here
range from a minimum value of −3.21 MJ·kg−1 [4] to a
maximum value of −4.832 MJ·kg−1 [14]. The average
value of the detonation energy in the literature is −4.4
MJ·kg−1
In the case of TNT, the detonation enthalpy of de-
composition calculated by Kinney [6] underestimated the
energy by approximately 40%, whereas the decomposi-
tion calculated by K-J rule [1] overestimated the energies
by a factor of 1.3 compared to the average value of −4.4
MJ·kg−1. Using calculations based on liquid water, the
S-R rule led to deviations from the mean value between
1.4% and 5.5%. The difference of 1.4% is obtained by
taking the enthalpy of formation given by Akhavan [2].
The modified K-W rules show differences on the order
of 3.2% to 7.6%. Greater differences are obtained by
considering water as a gas in the calculations. Finally, for
a reference enthalpy, the range of differences between
calculations based on the Gibbs free enthalpy and the
enthalpy of the reaction varies by a factor of 2 between
the lower and upper bounds.
In the case of PETN, considering water as gas, the en-
ergy values ranged from −5.667 MJ·kg−1 [1] to −6.359
MJ·kg−1 [15], resulting in an average of −6.06 MJ·kg−1
(Table 4). Ornellas [16] reported a significantly higher
value that was not taken into account in calculating the
average. Scilly [1] obtained experimentally a detonation
energy value of −5.73 MJ·kg−1. The S-R (or K-J) rules
applied to the calculation of free energies correlates very
well (<1%) with this value for the enthalpies of forma-
tion reported in previous work [17-19]. For other data
[2,6,14], the differences range from 1.4% to 3%. The
differences in energy values calculated from the enthal-
pies of reaction are of the order of 3% to 7%. However,
Table 3. Enthalpy of formation and entropy for TNT and PETN.
TNT-H (kJ·mol−1) −26.00 [2]; −41.13 [20]; −54.40 [6]; −54.49 [21]; −59.47 [17]
TNT-S (J·mol−1·K−1) 272.00 [6]; 271.96 [21]; 554.00 [20]
PETN-H (kJ·mol−1) −477.05 [2]; −502.66 [14]; −514.63 [6]; −532.06 [17]; −538.50 [18,22,23]
PETN-S (J·mol−1·K−1) 129.36 [18]
Table 4. Detonation energy of PETN.
Detonation Energy
(MJ·kg−1) Experimental Value Theoretical Value
H2O Gas −5.73 [1]; −8.137 [16] −5.949 [17]; −6.359 [15]; −6.276 [24]; −5.9 [14]; −5.8 [9]; −5.667 [1]
H2O Liquid −6.234 [1]; −6.322 [17]; −6.19, −6.24, −6.30 [8] −6.404 [17]; −6.347[22]; −5.792 [2]

I. SOCHET ET AL. 35
if water is considered in its liquid form, application of
the K-W rule is in better agreement with the average
value, especially with the enthalpies calculated by Tarver
[19]. For other values of the enthalpy of formation, the
gap remains below 3%. The free energies applied to the
case of decomposition using the S-R (or K-J) rules have
a difference of 10% compared to experimental values [1,
8] or to the average value.
In conclusion, in the case of TNT, it is preferable to
adopt the S-R rules based calculation methods with the
assumption of liquid water using the thermochemical
data of Akhavan [2] where the enthalpy of formation is
lower. For PETN, it is preferable to use the K-W rules
with the assumption of liquid water and the enthalpy of
formation given by Tarver [19], which gives the best
correlation with respect to the average value.
In the absence of thermochemical data for ANFO, it
was not possible to carry out similar calculations to
compute the detonation energy. Kinney [6] reported
detonation energy of −5.197 MJ·kg−1.
3. Blast Waves in Free Air
3.1. Characteristics of Blast Waves Resulting
from Detonation
The pressure profile over time of an ideal blast wave can
be characterized by its rise time, the peak overpressure, the
positive phase duration and the total duration (Friedlander
wave). Thus, the change in pressure created by an explo-
sion at a fixed distance r from the center of the explosion
can be schematized by the following profile (Figure 1).
d
a
a
t
t
I
Pt






(5.1)
and the impulse of the rarefaction wave is given by the
following:
d
a
a
t
t
I
Pt









(5.2)
The terms of the compression wave and rarefaction
wave are important for analyzing the response of the
target under the action of the shock wave. The energy of
explosion, the density of energy released (the energy
volume of the load) and the power (the rate of release of
energy) are the source parameters that determine the am-
plitude, duration and other features of the blast wave.
The detonating explosives generate waves that are con-
sidered ‘near-ideal’ due to their high density compared to
air, and therefore the energy released per unit of volume
is significant.
The same analytical relationships have been estab-
lished to calculate the characteristics of the blast wave as
a function of distance (including pressure, duration and
impulse of the positive and negative phases).
A review of these approaches is proposed here. In the
context of this article, the study was limited to the pa-
rameters of pressure, impulse and the duration of the
positive phase of the blast wave of explosive spherical
charges in air, at high altitudes without ground effect.
Comparison of the main characteristics of blast waves
in this study has been restricted to TM5-855 (CONWEP)
[25] which supersedes TM5-1300 [26], AUTODYN code
[27] and software ASIDE [28]. CONWEP allows the
calculation of the effects of conventional weapons from
the curves derived from TM5-855, “Fundamentals of
Protective Design for Conventional Weapons” from the
US Army Engineer Waterwaps. The calculations can be
conducted for explosions at ground level or in the air.
The AUTODYN software is a code for digital nonlinear
dynamic analysis of unsteady shock waves, impact and
the dynamic response of structures. In this study, calcu-
lations using AUTODYN were performed for spherical
detonation of a 1 kg explosive charge (TNT, PETN and
ANFO) at distance up to 20 meters. Simulations were
made with an AUTODYN 1D model to refine the mesh
(1-mm and 0.5-mm) over a length of 20 meters. Pressure
gauges were regularly located and the pressure-time re-
sult files were processed to calculate the characteristic
parameters ASIDE, with criminalistic vocation, com-
bines the functionalities of a software and a data base. It
is based on the observation of the damage and the ele-
ments of evidence collected during investigations of way
to be able to evaluate the explosive load used. Contrary,
ASIDE can provide an estimate of the damage if the na-
In this diagram, a is the arrival time of the wave-
front, is the positive overpressure,
t
P 

 is the du-
ration of the positive phase,
I

is the positive momen-
tum, is the negative depression, P 

 is the dura-
tion of the negative phase and
I
 is the negative im-
pulse. The impulse compression phase is calculated us-
ing the following formula:
Figure 1. Pressure profile characteristic of the blast wave
resulting from detonation.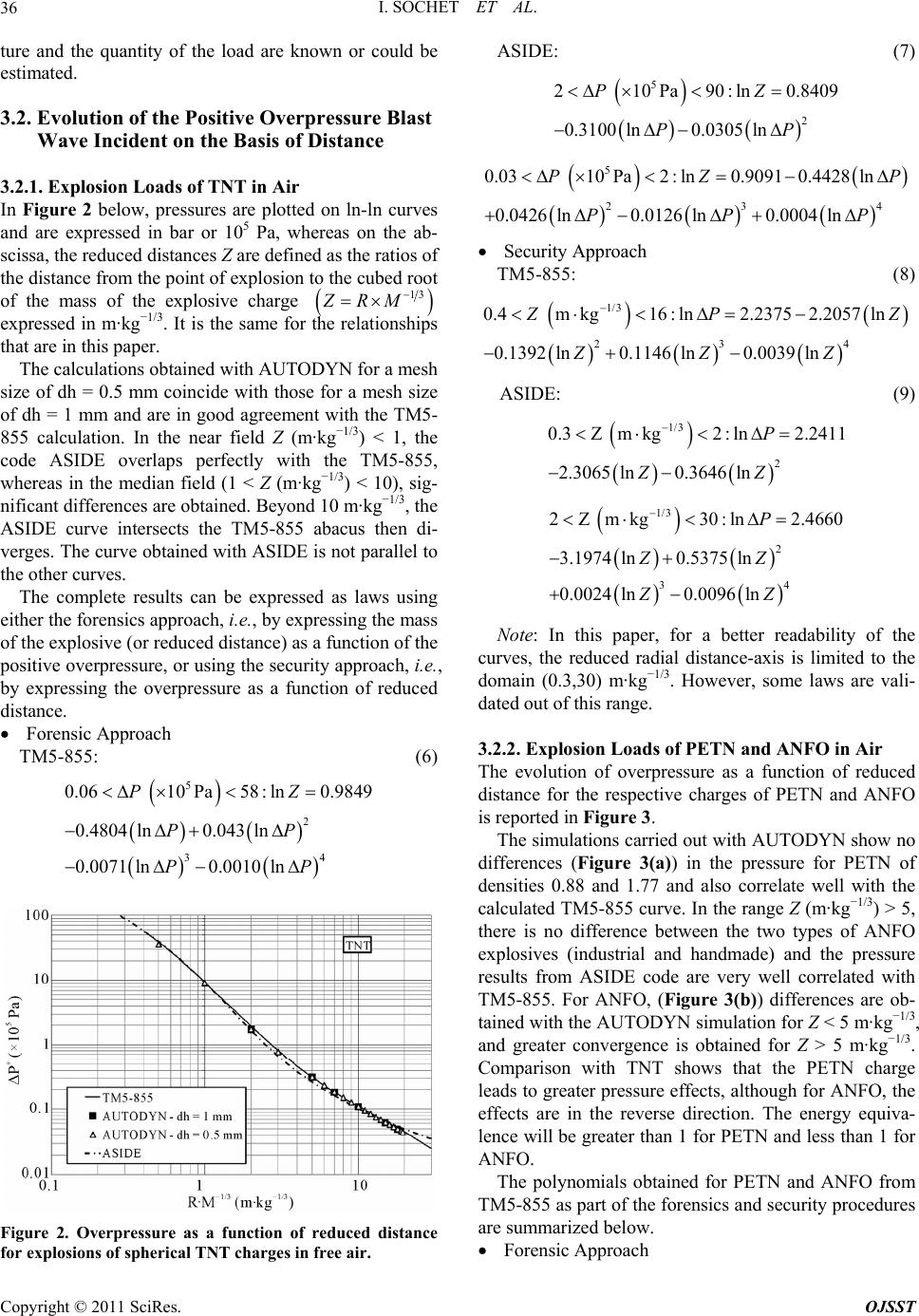

I. SOCHET ET AL. 36
ture and the quantity of the load are known or could be
estimated.
3.2. Evolution of the Positive Overpressure Blast
Wave Incident on the Basis of Distance
3.2.1. Explosion Loads of TNT in Air
In Figure 2 below, pressures are plotted on ln-ln curves
and are expressed in bar or 105 Pa, whereas on the ab-
scissa, the reduced distances Z are defined as the ratios of
the distance from the point of explosion to the cubed root
of the mass of the explosive charge

13
ZRM


expressed in m·kg−1/3. It is the same for the relationships
that are in this paper.
The calculations obtained with AUTODYN for a mesh
size of dh = 0.5 mm coincide with those for a mesh size
of dh = 1 mm and are in good agreement with the TM5-
855 calculation. In the near field Z (m·kg−1/3) < 1, the
code ASIDE overlaps perfectly with the TM5-855,
whereas in the median field (1 < Z (m·kg−1/3) < 10), sig-
nificant differences are obtained. Beyond 10 m·kg−1/3, the
ASIDE curve intersects the TM5-855 abacus then di-
verges. The curve obtained with ASIDE is not parallel to
the other curves.
The complete results can be expressed as laws using
either the forensics approach, i.e., by expressing the mass
of the explosive (or reduced distance) as a function of the
positive overpressure, or using the security approach, i.e.,
by expressing the overpressure as a function of reduced
distance.
 Forensic Approach
TM5-855: (6)
ASIDE: (7)


 
5
2
2 10Pa90:ln0.8409
0.3100 ln0.0305 ln
PZ
PP
 
 



 
5
23
0.03 10Pa2:ln0.90910.4428ln
0.0426 ln0.0126 ln0.0004 ln
PZ
PP 4
P
P

 
  
 Security Approach
TM5-855: (8)



 
1/3
234
0.4 mkg16:ln2.23752.2057ln
0.1392 ln0.1146 ln0.0039 ln
Z
PZ
ZZZ

 
 
ASIDE: (9)


 
1/3
2
0.3Z mkg2:ln2.2411
2.3065 ln0.3646 ln
P
ZZ

 



 
 
1/3
2
34
2Z mkg30:ln2.4660
3.1974 ln0.5375 ln
0.0024 ln0.0096 ln
P
ZZ
ZZ

 


Note: In this paper, for a better readability of the
curves, the reduced radial distance-axis is limited to the
domain (0.3,30) m·kg−1/3. However, some laws are vali-
dated out of this range.
3.2.2. Explosion Loads of PETN and ANFO in Air
The evolution of overpressure as a function of reduced
distance for the respective charges of PETN and ANFO
is reported in Figure 3.

 
 
5
2
34
0.06 10Pa58:ln0.9849
0.4804ln0.043 ln
0.0071 ln0.0010ln
PZ
PP
PP
 

 
The simulations carried out with AUTODYN show no
differences (Figure 3(a)) in the pressure for PETN of
densities 0.88 and 1.77 and also correlate well with the
calculated TM5-855 curve. In the range Z (m·kg−1/3) > 5,
there is no difference between the two types of ANFO
explosives (industrial and handmade) and the pressure
results from ASIDE code are very well correlated with
TM5-855. For ANFO, (Figure 3(b)) differences are ob-
tained with the AUTODYN simulation for Z < 5 m·kg−1/3,
and greater convergence is obtained for Z > 5 m·kg−1/3.
Comparison with TNT shows that the PETN charge
leads to greater pressure effects, although for ANFO, the
effects are in the reverse direction. The energy equiva-
lence will be greater than 1 for PETN and less than 1 for
ANFO.
The polynomials obtained for PETN and ANFO from
TM5-855 as part of the forensics and security procedures
are summarized below.
Figure 2. Overpressure as a function of reduced distance
for explosions of spherical TNT charges in free air.  Forensic Approach

I. SOCHET ET AL. 37
(a) (b)
Figure 3. Overpressistance in free air.
PETN-TM5-855: (10)
A NFO-TM5-855: (11)
P
 Security Approach
(12)
ure spherical charges of PETN and ANFO as a function of reduced d


 
1/3
23
10 mkg30:ln1.6259
2.4095 ln0.4477ln0.0605 ln
ZP
Z
ZZ

 


5
 
2
11 10Pa65:ln0.8156
0.2371 ln0.0421 ln
PZ
PP
 
 

 
 
5
2
34
0.02 10Pa11:ln1.0755
0.4397 ln0.0557 ln
0.0163 ln0.0043 ln
PZ
PP
PP
 
 
 

5
 
23
0.1 10Pa5:ln0.9303
0.4768 ln0.0344 ln0.0085 ln
PZ
PP
 
 
3.3. Evolution of the Duration of the Incident
Blast Wave as a Function of Distance in the
Positive Phase
The positive phase duration is typically reported as the
bed root of the mass of the explosive. The graph
in
altho
ve ith reduced distance. The duration
cu
shown below in Figure 4 indicates that developments
positive phase durations are more difficult to characterize,
ugh the overall trend shows that the duration posi-
phase increases wti
also approaches an asymptote in the far and near field.
The simulations with AUTODYN show that the posi-
tive phase durations are underestimated compared to the
references in TM5-855. In addition, there is a visibly
large gap for short distances less than 3 m·kg−1/3.
Regardless of the explosive (i.e., PETN or ANFO),
changes in the duration of the positive phase of the blast

 
5
2
0.02 10Pa1.7:ln0.7899
0.6296 ln0.0175 ln
PZ
PP
 
 
P ETN-TM5-855:

1/3
 
2
0.4 mkg2:ln
2.41472.2208 ln0.3184 ln
ZP
Z
Z 

 

 
 
1/3
2
34
2 mkg30:ln2.4038
2.1387 ln0.3354 ln
0.2848 ln0.0452 ln
ZP
ZZ
ZZ

 


ANFO-TM5-855: (13)

1/3
 
 
 
2
34
0.4 mkg10:ln2.0892
2.2328 ln0.1259 ln
0.1206 ln0.0030 ln
ZP
ZZ
ZZ


Figure 4. Duration of the reduced distance function for
explosions of spherical TNT charges in free air.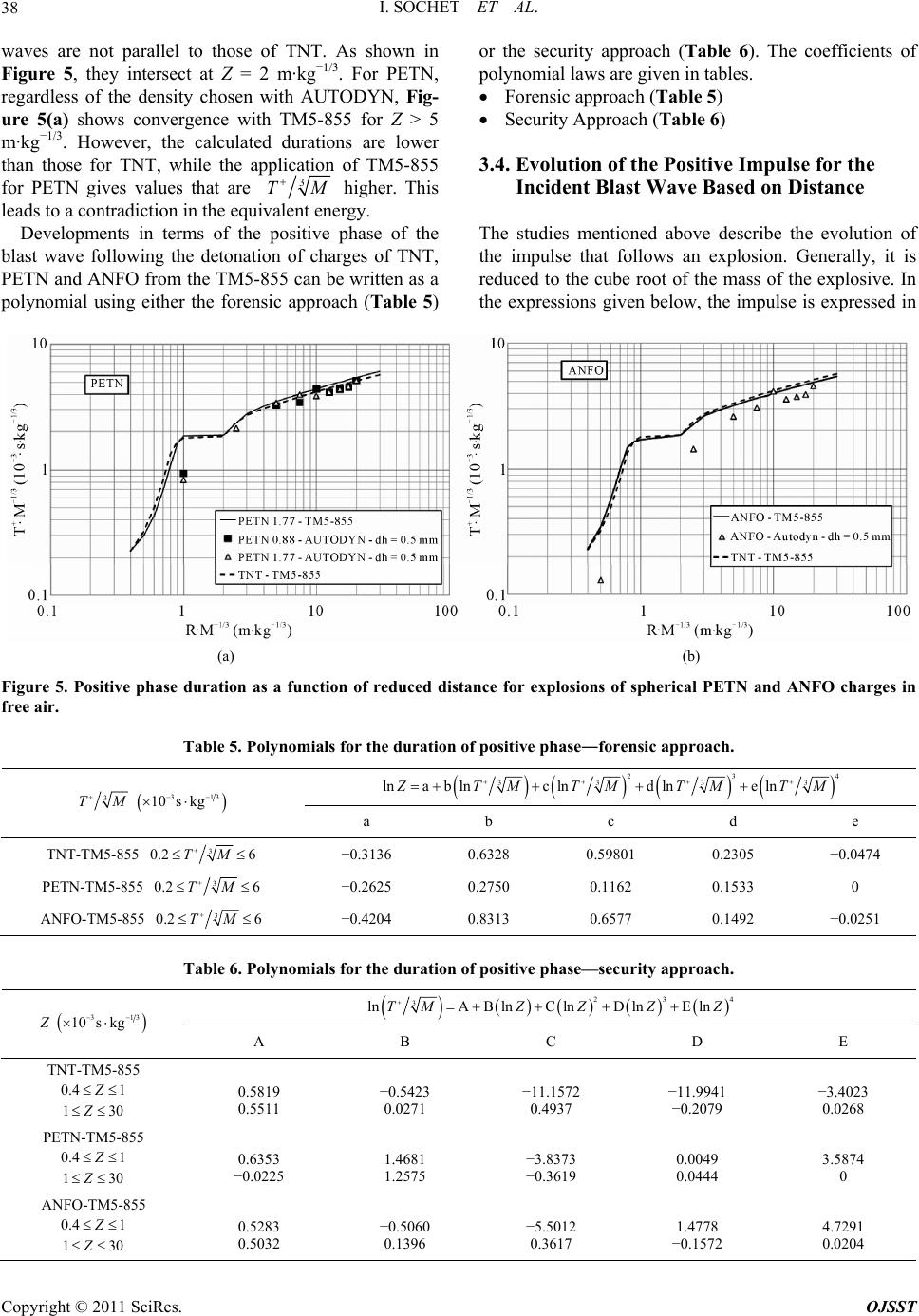

I. SOCHET ET AL. 38
waves are not parallel to those of TNT. As shown in
Figure 5, they intersect at Z = 2 m·kg−1/3. For PETN,
regardless of the density chosen with AUTODYN, Fig-
ure 5(a) shows convergence with TM5-855 for Z > 5
m·kg−1/3. However, the calculated durations are lower
than those for TNT, while the application of TM5-855
for PETN gives values that are 3 TM

valent ener
higher. This
leads to a contradiction in the equigy.
Developments in terms of the positive phase of the
blast wave following the detonation of charges of T
PETN and ANFO from the TM5-855 can be written as a
polynomial using either the forensic approach (Table 5)
6). The c

scribe the evolution of
losion. Generally, it is
duced to the cube root of the mass of the explosive. In
in
or the security approach (Table oefficients of
polynomial laws are given in tables.
T
Forensic approach (Table 5)
 Security Approach (Table 6)
3.4. Evolution of the Positive Impulse for the
Incident Blast Wave Based on Distance
NT, the impulse that follows an exp
he studies mentioned above de
re
the expressions given below, the impulse is expressed
(a) (b)
Figure 5. Positive phase duration as a function of reduced distance for explosions of spherical PETN and ANFO charges in
free air.
Table 5. Polynomials for the duration of positive phase―forensic approach.






23
33 3
lnab lnclnd lneln
4
3
Z
TM TMTMTM
 
 

313
3 10skgTM



a b c d e
3
0.2 6M −0.3136 0.6328 0.59801 T

0.2305 −0.0474 TNT-TM5-855
PETN-TM5-855 3 0.2 6TM

 −0.2625 0.2750 0.1162 0.1533 0
ANFO-T 3 0.2 6TM

 −0.4204 0.8313 0.6577 0.1492 −0.0251 M5-855
Table 6. Polynomials for the duration of positive phase—security approach.


 
23
3
lnAB lnC lnD lnElnTMZ ZZZ

4

31
10skgZ 
3
A B C D E
TNT-TM5-855
0.5819
0.5511
5423
271
−11.1572
0.4937
−11.99
−0.20
−3.4023
0
0.4 1Z
130Z
−0.
0.0
41
79 .0268
PETN-TM5-
0.4 1Z
855
0
3.5874
0
ANFO-TM5-855
0
0.5283
0.2
−0.5060
0.6
−5.5012
0.7
1.4778
−0.2
4.7291
0.4
13Z
0.6353
−0.0225
1.4681
1.2575
−3.8373
−0.3619
0.0049
0.0444
0.4 1Z
13Z 503139361157 020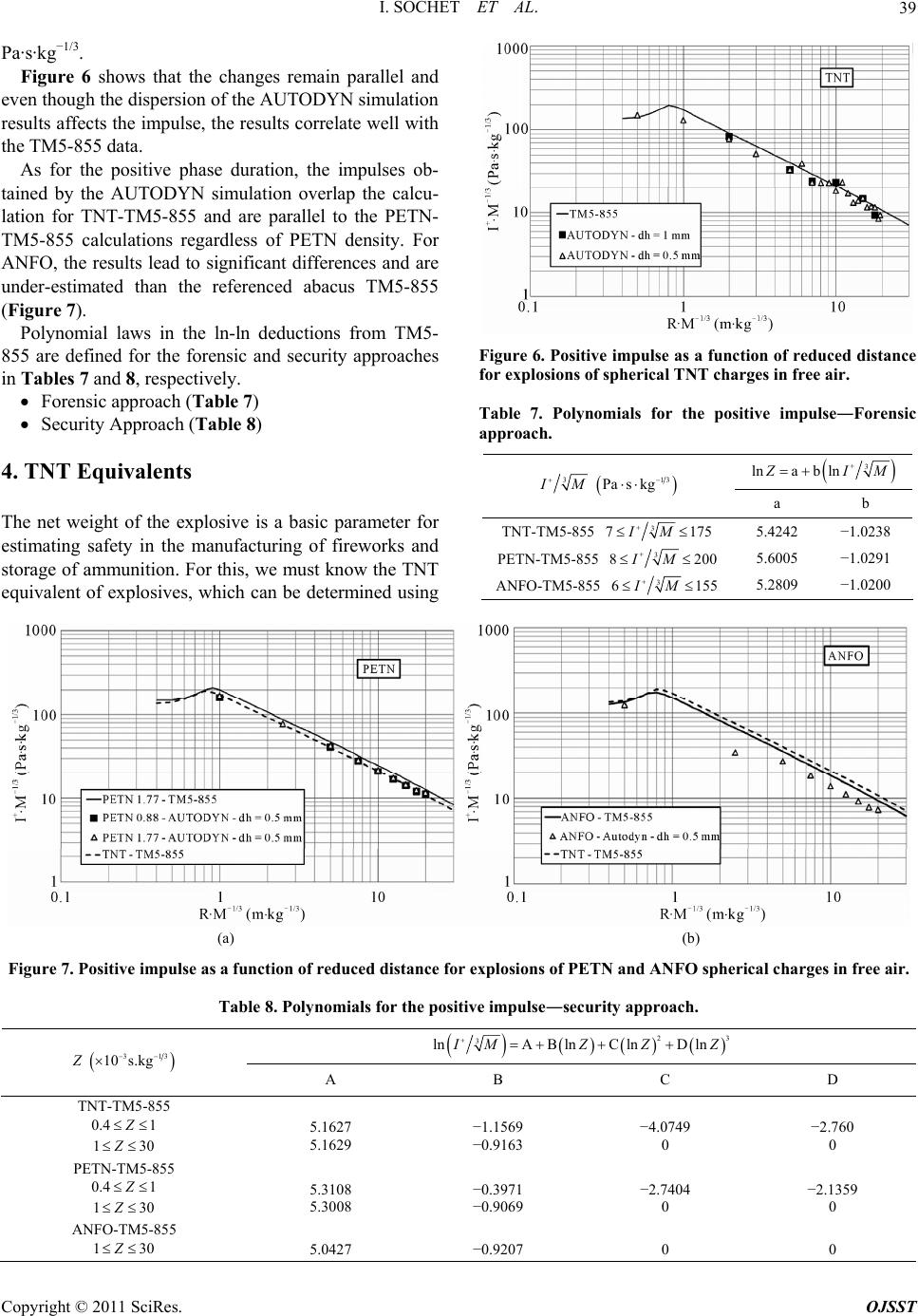

I. SOCHET ET AL.39
Pa·s·k
Figure 6 shows that the chremain parallel and
even though the dispersion of TODYN sim
resulate well with
the TM5-855 da
As for the positive phase duration, the impulses ob-
taineDYN simuloverlap the calcu-
lation for TNT-855 and allel to the PETN-
ulations regardless of PETN density. For
in
n be determined using
g−1/3.
anges
the AUulation
ts affects the impulse, the results correl
ta.
d by the AUTOation
TM5- are par
TM5-855 calc
ANFO, e thresults lead to significant differences and are
under-estimated than the referenced abacus TM5-855
(Figure 7).
Polynomial laws in the ln-ln deductions from TM5-
855 are defined for the forensic and security approaches
Tables 7 and 8, respectively.
 Forensic approach (Table 7)
 Security Approach (Table 8)
4. TNT Equivalents
The net weig
Figure 6. Positive impulse as a function of reduced distance
for explosions of spherical TNT charges in free air.
Table 7. Polynomials for the positive impulse―Forensic
approach.
ht of the explosive is a basic parameter for
estimating safety in the manufacturing of fireworks and
storage of ammunition. For this, we must know the TNT
equivalent of explosives, which ca

3
lnabln
Z
IM




13
3 PaskgIM


a b
3
71IM

 75
5.4242 −1.0238
TNT-TM5-855
PETN-TM5-855 3 8 200IM

 5.6005 −1.0291
ANFO-TM5-855 3 6155IM

 5.2809 −1.0200
(a) (b)
Figure 7. Positive impulse as a function of reduced distance for explosions of PETN and ANFO spherical charges in free air.
Table 8. Polynomials for the positive impulse―security approach.



23
3
lnAB lnClnD ln
I
MZZ
 Z

313
10s.kgZ 
A B C D
TNT-TM5-855
0
−2.760
0
0.4 1Z
13Z
5.1627
5.1629
−1.1569
−0.9163
−4.0749
0
PETN-TM5-855
0.4 1Z
0
5.3108 −0.3971 −2.7404 −2.1359
0
ANFO-TM5-855
0 5.0427 −0.9207 0 0
13Z 5.3008 −0.9069 0
13Z

I. SOCHET ET AL. 40
several approaches. Generally, the TNT equivalent is the
mass of TNT that proides an equal amount of energy
during the explosion as the unit mass of tplosive in
question. the TNT equivalen
the ratio of the mass of TNT to the mas explosive
that leads to tmplitude of a ter of the
blast wav impulse) at the samdial dis-
tance for each charge assuming the scals of Sachs
and Hopivalent mass of prsure [29] for
n explosive is then given as follows:
every unknown explosive in accordance with the Allied
v
he ex
Specifically, t is defined as
s of the
he same a
e (pressurer
parame
oe ra
ing law
kinson. The eques
Ammunition Storage and Transport Publication [32].
rmby and Wharton [33] and Wharton al. [34]
based their calculation o the TNT equivalent used in the
a approach fotypes of conplo-
nd identified lin trends of TNT eq
pressure anse as a functioduced
e.
egarding the explosives studied in this work, the de-
ent of overpressure and impulse as a function of a
3
TNT
PTNT
P
cst
MZ
ETNT MZ

 


where Z is the reduced distance. A similar approach is
conducted for the equivalent mass of impulse as follows:
3
TNT
ITNT
I
cst
MZ
ETNTMZ

 


However, when the impulses are reported as a cubed
root of the mass, the equivalent impulses can be obtained
by sliding the curves along the first diagonal. Esparza
[29] conducted a study of several condensexplosives d e
(Composition B, PBX-9404, PETN, TNT, PBX 9501,
PBX 9502) and presented the average values of an
equivalent TNT pressure range of 0.9 to 1.7 for these
explosives, whereas the impulses, in terms of TNT
equivalent, range from 0.6 to 1.2. This is robably the p
easiest method, but it only applies for explosives with the
same geometry.
However, Gelfand [9] defines the energy equivalent of
TNT as the ratio of the detonation energy of an explosive
and the detonation energy of TNT.
Taking into account the equation of detonation prod-
ucts, it can be shown that the effects of detonation are
influenced by the basic parameters of detonation speed,
pressure, detonation energy and the number of moles of
gaseous detonation products. These values can be ob-
tained from thermochemical calculations and it is possi-
ble to obtain an average value.
12 34
H
EHEHEHE
TNT TNT
nEPD
ETNT kkkk
nEPD

TNT TNT
where k1, k2, k3 and k4 are empirical coefficients obtained
experimentally [30].
The difficulty of estimating a single value for TNT
equivalents is confirmed by Peugeot et al. [31], who de-
scribe the parameters influencing the equivalent value,
namely the composition of the material energy, the dis-
tance and the geometry of the load. If the energy equiva-
lent cannot be measured or estimated, then a TNT
equivalent energy factor of 1.4 leads to a reasonable and
Fo et
n
Esparzr other densed ex
sives aearuivalents in
terms of d impuln f reo
distanc
R
velopm
reduced distance for PETN and ANFO are parallel to
those of TNT. Therefore, TNT equivalent means can eas-
ily be deduced for each of the characteristic parameters of
the blast wave with the exception of the positive duration.
 For overpressure, TNT energy equivalents of 1.14
and 0.90 are obtained for PETN and ANFO, respect-
tively, by sliding the PETN or ANFO pressure curves
along the abscissa Z.
 For duration and impulse positive phase, the parame-
ters are reduced to the cubed root of mass, and thus,
the curves of PETN and ANFO are slid along the di-
agonal. Impulse energy equivalents of 1.15 and 0.90
are obtained for PETN and ANFO, respectively.
However, in case of reduced duration an average
equivalent TNT cannot be obtained because the curve
of the explosive is either above or below the curve
corresponding to TNT (Figure 5). There are two
emerging areas for which it is possible to define a
TNT equivalent. In the case of PETN, for Z < 0.9
m·k g−1/3 the equivalent is 0.95 (Figure 5(a)) and for Z >
5 m·kg−1/3 it is 1.06. In the case of ANFO (Figure
5(b)), the equivalent is 1.1 if Z ≤0.9 m·kg−1/3.
 The TNT equivalent energies obtained in this study
are in good agreement with values reported in the lit-
erature (Table 9) in terms of pressure and impulse for
ANFO. In case of PETN, the calculated TNT equiva-
lent is smaller than the reported values (Table 9).
5. Conclusions
First, the computation of the detonation energy reported
in this study has permitted us to compare different de-
composition rules and thermodynamic data to underline
the energy discrepancy for the three explosives studied
(TNT, PETN, ANFO). In addition, the computation
demonstrates the importance of clarifying the choice
between the theoretical and experimental conditions.
Second, this study has identified the analytical solu-
tions and the available abacus to estimate the effects of
exploding pyrotechnic charges in terms of the overpres-
sure, duration and impulse of the positive phase. Com-
parison of the main characteristics of blast waves in this
conservative estimate of the equivalent TNT mass for study is focused on the TM5-855 (CONWEP), AUTO

I. SOCHET ET AL.41
Table 9. TNT equivalent energ
TN
ies obtained in this study.
T Equivalent
Explosive
Pressure Impulse Global
PETN 1.27 [15,25,32,35]; 1.33, 1.45 - 1.73 [9] 1.28 [9]
ANFO 0.82 [15,25,35]; 0.83 [32]; 0.83 for DP = 2.07 at 13.8 bar and 0.59 for DP > 13.8 bar [36] 0.82 [1] 0.70 [36] 0.75 [9]
DYN and ASIDE codes.
Comparison with TNT shows that PETN charges lead
to higher pressures than TNT, whereas ANFO shows
lower pressures.
AUTODYN simulations show that the effects of
Acorrelate well in terms of the duration and NFO do not
imherefore, the simulation of ANFOs pulse. T charge
detonation must be examined with caution, and for ex-
ample in a next step it is possible to consider a refined
mehoish, the cce of the state equation and the complex
composition of ANFO.
Polynomial laws have been established based on two
approaches, one forensic-based and the other security-
based. In the first, the reduced distance is expressed in
terms of characteristic quantities of the explosive and in
the second, the quantities of the explosive are expressed
in terms of reduced distance.
6. References
[1] N. F. Scilly, “Measurement of the Explosive Performance
of High Explosives,” Journal of Loss Prevention in the
Process Industries, Vol. 8, No. 5, 1995, pp. 265-273.
doi:10.1016/0950-4230(95)00031-U
[2] J. Akhavan, “The Chemistry of Explosive,” 2nd Edition,
Royal Society of Chemistry (Great Britain), 2004.
[3] A. Lannoy, “Effet des Explosions sur les Structures,
Extrapolation de l’Abaque du TM5-1300,” EDF, Dir.
Etudes et Recherches, 1979.
“Post Detonation and Thermal Studies of
plosives in a Closed Chamber,” 6th Int
national Symposium on Coal Combustion, Yale Univer-
[4] W. S. Filler,
Solid HIgh Exer-
sity, New Haven, 1956, pp. 648-657.
[5] DoD standard TNTe, 1998.
http://www.fas.org/man/dod,101/navy/docs/es310/chemis
try/chemistry.htm
[6] G. F. Kinney and K. J. Graham, “Explosives Shocks in
Air,” 2nd Edition, Springer-Verlag, Berlin, 1985.
[7] F. P. Lees, “Loss Prevention in the Process Industries,
Hazard Identification, Assessment and Control, Vol. 2,”
2nd Edition, Butterworth Heinemann, Oxford, 1996.
Analysis, Vo
doi:10.1007/BF02549223
[8] Y. Tongchang, Y. Menchao and W. Jianling, “Determi-
nation of Heats of Detonation and Influence of Compo-
nents of Composite Explosives on Heats of Detonation of
High Explosives,” Journal of Thermal l. 44,
No. 6, 1995, pp. 1347-1356.
[10] W. E. Baker, “Explosions in Air,” University of Texas
[11] H. Pförtner, “Gas Cloud Explosions and Resulting Blast
,” Nuclear Engineering and Design, Vol. 41, No. 1,
1977, pp. 59-67. doi:10.1016/0 (77)900
[9] B. Gelfand and M. Silnikov, “Blast Effects Caused by
Explosions” United States Army, European Research Of-
fice of the US Army, London, 2004.
Press, Austin, 1973.
Effects
029-5493 94-2
[12] S. Trélat, “Impact de Fortes Explosions sur les Bâtiments
’Une Installation dustrielle,”e
d’O 006
[13] M. Omang, S.O. Christensen, S. Borve and J. Trulsen,
plosions: A Comparative Study of
Représentatifs dIn Thèse d
Doctorat, l’Université rléans, Orléans, 2.
“Height of Burst Ex
Numerical and Experimental Results,” Journal Shock
Waves, Vol. 19, No. 2, 2009, pp. 135-143.
doi:10.1007/s00193-009-0196-8
[14] N. Kubota, “Propellants and Explosives,” 2nd Edition,
Wiley-VCH, Weinheim, 2007.
[15] G. Parmentier, “Synthèse des Résultats Expérimentaux
Relatifs aux Détonations d’Explosifs Sphériques,”Institut
Franco-Allemand de Recherche de Saint-Louis, 1993.
[16] J. D. Ornellas, “The Heat and Products of Detonation of
Cyclotat ramethyle netetra nitramine, 2,4,6-Trinitrotoluene,
Nitromethane, and Bis[2,2-dinitro-2-fluoroethyl]formal,”
Journal Physical Chemistry, Vol. 72, No. 7, 1968, pp.
2390-2394. doi:10.1021/j100853a019
[17] R. Meyer, “Explosives,” 3rd Edition, VCH-Verlag, Wein-
heim, 1987.
[18] National Institute of Standards and Technology, National
Institute of Standards and Technology. www.nist.gov/
[19] C. M. Tarver, T. D. Tran and R. E. Whipple, “Thermal
Decomposition of Pentaerythritol Tetranitrate,” Propel-
lants Explosives Pyrotechnics, Vol. 28, No. 4, 2003, pp.
189-193. doi:10.1002/prep.200300004
[20] American Society for testing and Materials (ASTM), The
ASTM Computer Program for Chemical Thermodynamic
and Energy Release Evaluation CHETAH 7.3, 2001.
[21] NASA Lewis Research Center.
http://www.me.berkeley.edu/gri_mech/data/thermo_table.
html
[22] P. W. Cooper, “Explosives Engineering,” Wiley-VCH,
f
[24] J. Yinon and S. Zitrin, “Modern Methods and Applica-
Weinheim, 1996.
[23] M. Finger, E. Lee, F. H. Helm, B. Hayes, H. Horning, R.
McGuine, M. Kahara and M. Guidry, “The Effects o
Elemental Composition on the Detonation Behavior of
Explosives,” Sixth Symposium (International) on Detona-
tion, ACR-221, 1976, p. 710.

I. SOCHET ET AL. 42
ctive Design for
DC, 1987.
S
y for
led Distances,” Interna-
0. doi:10.1016/0734-743X(86)90025-4
tions in Analysis of Explosive,” Wiley, Hoboken, 1996.
[25] TM5-855-1, “Fundamentals of Prote
Conventional Weapons,” US Department of the Army,
Washington
[26] TM5-1300, “The Design of Structures to Resist the Ef-
fects of Accidental Explosions,” Technical Manual, U
Department of the Army, the Navy and the Air Force,
Washington DC, 1990,
[27] AUTODYN, Software for Non-Linear Dynamics, Pro-
prietary to ANSYS.
[28] ASIDE, Forensic Software Database for Crime Scene
Investigation, Proprietary of IRCGN.
[29] E. D. Esparza, “Blast Measurements and Equivalenc
Spherical Charges at Small Sca
tional Journal of Impact Engineering, Vol. 4, No. 1, 1986,
pp. 23-4
lent of High Explosives,” Scien
eristics
98.
[30] R. Jeremié and Z. Bajié, “An Approach to Determining
the TNT Equivatific
Technical Review, Vol. 56, No.1, 2006, pp. 58-62.
[31] F. Peugeot, E. Deschalbault and P. F. Péron, “TNT
Equivalency: Misconceptions and Reality, Munitions
Safety Information Analysis Center,” Munitions Safety
Information Analysis Center (MSIAC) Unclassified, Re-
port L-132, October 2006.
[32] Allied Ammunition Storage and Transport Publication
(AASTP), 4, Explosives Safety Risks Analysis, Part II,
AC/258(ST)WP/221, 2003.
[33] S. A. Formby and R. K. Wharton, “Blast Charact
and TNT Equivalence Values for Some Commercial Ex-
plosives Detonated at Ground Level,” Journal of Haz-
ardous Materials, Vol. 50, No. 2-3, 1996, pp. 183-1
doi:10.1016/0304-3894(96)01791-8
[34] R. K. Wharton, S. A. Formby and R. Merrifield, “Airblast
TNT Equivalence for a Range of Commercial Blasting
Explosives,” Journal of Hazardous Materials, Vol. 79,
No. 1-2, 2000, pp. 31-39.
doi:10.1016/S0304-3894(00)00168-0
[35] P. Naz, “Etude de Souffle des Têtes Explosives. Etude
Bibliographique,” Institut Franco-Allemand de Recherche
, Saint-Malo, 23-27
de Saint-Louis, Saint-Louis, 2005.
[36] J. Mory, R. Branka, “Les Equivalents TNT des Explosifs
Intentionnels et des Produits Chimiques Condensés
Solides ou Liquides à Risque d’Explosion,”Europyro 8th
Congrès International de Pyrotechnie
June 2003, pp. 407-440.