ABSTRACT

We present a numerical method based on genetic algorithm combined with a fictitious domain method for a shape optimization problem governed by an elliptic equation with Dirichlet boundary condition. The technique of the immersed boundary method is incorporated into the framework of the fictitious domain method for solving the state equations. Contrary to the conventional methods, our method does not make use of the finite element discretization with obstacle fitted meshes. It conduces to overcoming difficulties arising from re-meshing operations in the optimization process. The method can lead to a reduction in computational effort and is easily programmable. It is applied to a shape reconstruction problem in the airfoil design. Numerical experiments demonstrate the efficiency of the proposed approach.

Keywords:

Immersed Boundary Method, Genetic Algorithm, Bezier Curve, Elliptic Dirichlet Boundary Value Problem, Shape Optimization Problem

1. Introduction

The aim of shape optimization is to find a shape Ω such that the structure represented by Ω behaves in an appropriate way. Usually this goal is realized by the minimization of a suitable cost functional J over an admissible family 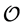of domains, in which all possible candidates are included. Schematically, shape optimization problem can be expressed as follows:

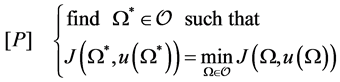
where is the solution of a state equation. In this paper, the state equation is formulated by an elliptic equation with Dirichlet boundary condition. Shape optimization problems have been extensively studied from the mathematical point of view [1]. Our paper deals with their practical aspects. The practical shape optimization problem in this paper is a reconstruction problem, in which the target is to find the shape of airfoil when the pressure distribution on it is given.

Our optimization is performed by using genetic algorithm (GA) [2] [3]. GA is very popular at present for its simplicity and ability to handle large scale problems. It is a global optimization method, and can be used to solve non-smooth optimization problems. Because GA is based on cost functional evaluations. The state equations need to be repeatedly solved on different domain changing during shape optimization computations.

The numerical solution of partial differential equations describing the fluid flow is usually done by performing spatial and temporal discretization. The spatial representation must take into account for the boundaries of the computational domain and then make use of a discrete representation via meshing. Solving the flow around objects with complex shapes may involve extensive meshing work that has to be repeated each time a change in the geometry is needed. Important benefit would be reached if we are able to solve the flow without the need of generating a mesh that fits the shape of the immersed objects. Most flow solvers are based on body-conforming grids (i.e. the external boundary and surfaces of immersed bodies are represented by the mesh faces), but there is an increased interest in solution algorithms for non-body-conforming grids. Such methods are presented under a variety of names: immersed boundary (IB), immersed interface, embedded mesh, fictitious domain, all having in common the fact that the spatial discretization is done over a single domain containing both fluid and solid regions and where mesh points are not necessarily located on the fluid-solid interface.

We use the Lagrange multiplier-based fictitious domain method [4] [5] for solving the state equation in the shape optimization problem. The fictitious domain method based approach in the shape optimization problem can be found in [6] [7]. Furthermore in order to avoid costly and sometimes extremely difficult meshing work on body-fitted geometries, we incorporate the technique of the IB method into the framework of the fictitious domain method.

The IB method was initially introduced by Peskin [8] [9] for finite differences applied to fluid-structure interactions. The method received particular attention in recent years [10] [11] [12]. Peskin’s IB method was developed for the comput- er simulation of general problems involving a transient incompressible viscous fluid containing an immersed elastic interface, which may have time-dependent geometry or elastic properties, or both. The IB method is at the same time a mathematical formulation and a numerical scheme. The mathematical formulation is based on the use of Eulerian variables to describe the dynamic of fluid and of Lagrange variables along the moving structure. The force exerted by the structure on the fluid is taken into account by means of a Dirac delta function constructed according to certain principles. The main idea is to use a regular Eulerian mesh for the fluid dynamics simulation, coupled with a Lagrangian representation of the immersed boundary. The advantage of this method is that the fluid domain can have a simple shape, so that structured grids can be used. The Lagrangian mesh is independent of the Eulerian mesh. The interaction between the fluid and the immersed boundary is modeled by using a well-chosen discrete approximation to the Dirac delta function.

In our approach, all domains 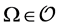are embedded into a fictitious domain 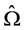with a simple shape (e.g. a box). It is easy to construct a triangularization of such a domain. The triangularization is fixed, i.e., it does not change during an optimization computation. All computations for solving the state problem are performed in 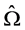with the same stiffness matrix, which also does not change and consequently can be computed and stored for ever. The method has the advantage of avoiding the need for re-meshing procedures in the optimization process. The necessary information on the geometry is encoded in an additional variable, contributing only to the right hand side of the state equations. We show that the resulting model can be very efficient for optimization computations. Numerical experiments demonstrate the efficiency of the proposed approach.

The paper is organized as follows. In Section 2, the state equation is presented by an elliptic equation with Dirichlet boundary condition. We describe its algorithm based on boundary Lagrangian fictitious domain method. We incorporate the technique of the immersed boundary method into the framework of the fictitious domain method. In Section 3, we consider the airfoil design for the two- dimension incompressible inviscid uniform flows. We describe the mathematical formulation of a shape optimization problem. In Section 4, we do numerical experiments to show that our proposed method is feasible and effective for solving the shape optimization problem.

2. Fictitious Domain Based Approach

On a domain, assume problem [P] with 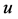being the solution of the following elliptic equation with Dirichlet boundary condition:

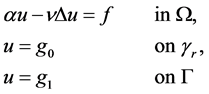(1)

where domain Ω is the exterior of an obstacle B with boundary 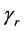(see Figure 1), 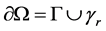, and Γ is the boundary of a rectangle. The 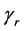is defined by the design variable, , where U is the set of admissible design parameters.

We require that the set U is compact. Coefficient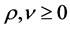, , 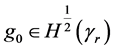,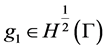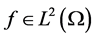. For simplicity, is sometimes denoted by.

Since the solution, , dependents on parameter, it is also denoted by, , or simply,.

According to the boundary Lagrangian fictitious domain method [5], the Dirichlet boundary condition on is enforced by using Lagrangian multiplier on the boundary. We can consider the problem in the extended rectangular domain:. Problem (1) is equivalent to the following variational problem:

Find, such that

(2)

(3)

where, , . The and are the extensions of and in, respectively, and,.

The problem (2)-(3) can be solved by GCG iterative method. We describe the algorithm presented by [13] as follows:

Algorithm 0:

Step 0: Initialization.

・ Set initial Lagrangian multipliers: and a number small enough for the convergence criterion.

・ Find by

(4)

・ Calculate by

・ Set the initial descent direction.

To obtain, , and from, , and, one proceeds as follows:

Step 1: Find descent direction.

・ Solve by

(5)

・ Calculate by

(6)

・ Find the new solution by

・ Calculate the new gradient by

Step 2: Construct convergence criterion and update descent direction.

If, then take the solution being, . Otherwise

Set and return to Step 1.

It can be seen from the above algorithm that we need calculate elliptic variational problems (4) and (5). Conventionally we solve them by the finite element method. In the computation procedure of the finite element discretizations, the mesh of the extended domain is constructed from a rectangular triangulated mesh by locally fitting this mesh to the irregular obstacle boundary. The conventional finite element discretizations result the problem in the solution of huge algebraic system of equations and will meet the trouble of computing the boundary integrals. In order to avoid these difficulties and solve more efficiently the extended problem, we will incorporate the technique of the immersed boundary method into the framework of the fictitious domain method. The main idea is to use Dirac delta function to improve the computation procedure of the discretizations. We describe the algorithm presented by [13] as follows.

We construct a regular Eulerian mesh on

where is the mesh width (for convenience, kept the same both in - and in -directions). Assume the configuration of the simple closed cure is given in a parametric form,. The discretization of the boundary employs a Lagrangian mesh, represented as a finite collection of Lagrangian points, , apart from each other by a distance, usually taken as being.

Let be a Dirac delta function. In the following calculation procedure, is approximated by the distribution function. The choice here is given by the product (see [10])

where

Using the above Dirac delta function we can transfer the weak forms of the partial differential equations (4) and (5) to the strong forms and then solve them by Fast Poisson Solvers such as the fast Fourier transform or cyclic reduction. In mathematical view, we need the following Lemma (see [14]).

Lemma 1. Assume that the simple closed cure, the configuration of which is given in a parametric form, is Liplischit continuous, . Then defined by

is a distribution function belonging to defined as follows: for all

By Lemma 1, we can write the right hand in (5) as following form:

where

(7)

That is, calculated over the Lagrangian points are distributed over the Eulerian points by (7). Thus we can write (5) in the strong form below:

(8)

In the same way, (4) also can be written in the strong form below:

(9)

where

(10)

Note that (8) and (9) are defined in the rectangular domain. We can solve their discrete forms by Fast Poisson Equation Solvers such as the fast Fourier transfer or cyclic reduction on Cartesian mesh. In order to calculate in (6), we calculate over Lagrangian points, by over neighboring Eulerian points obtained by (8). We use the following formula due to the property of (see [10]),

(11)

The discrete form of (7) is

(12)

The discrete form of (10) is

(13)

The discrete form of (11) is

(14)

Based on the above analysis, we have the discrete algorithm of GCG for solving (2)-(3) as follows:

Algorithm 1:

Step 0: Initialization.

1) Distributed over the Lagrangian points to the Eulerian points by (13).

2) Calculate (9) for over the neighboring Eulerian points of the boundary.

3) Calculate over Lagrangian points by over neighboring Eulerian points by using

(15)

4) Calculate over Lagrangian points by

5) Set the initial descent direction,.

To obtain, , and from, , and, one proceeds as follows:

Step 1: Find descent direction.

1) Distributed over the Lagrangian points to the Eulerian points by (12).

2) Solve (8) for over the neighboring Eulerian points of the boundary.

3) Calculate over Lagrangian points by over neighboring Eulerian points by using (14).

4) Calculate by

5) Let

6) Calculate the new gradient by

Step 2: Construct convergence criterion and update descent direction. For given small enough, if, then take over the Lagrangian points, and calculate its correspondent solution by using

where

Otherwise

Set and return to Step 1.

It can be seen from steps 4, 5, and 6 in Step 1 that the calculations are done over the Lagrangian points and we need solve (8) only for over the neighboring Eulerian points of the boundary when we use FFT. Thus the above approach can lead to a significant reduction in computational effort and memory requirement. It need not make use of the finite element discretizations. The main advantage of the proposed method is that in the optimization process Eulerian mesh on is fixed unlike in many of the other approaches such as obstacle fitted meshes and solution procedure is often efficient. The proposed method has a simple structure and is easily programmable.

3. Shape Optimization Problem

Our shape optimization problem is a shape reconstruction problem. We consider the airfoil design for the two-dimension incompressible inviscid uniform flows. We want to find the shape of an airfoil when the pressure coefficient on is known. Below we will give the formulation of this problem.

Suppose the uniform flow around an arbitrary airfoil B is from the left toward the right and of velocity profile. For the discretization computation, this exterior problem is truncated by introducing an artificial boundary which is a rectangle. The domain is the rectangle excluding the airfoil B with boundary, whose leading edge is in origin (see Figure 1). By formulating this problem for stream function, the corresponding partial differential equation with Dirichlet boundary condition is:

(16)

In order to solve the shape optimization problem numerically, the boundary must be parametrized using a finite number of design parameters. Let the vector of design parameter define the boundary curve. One possible way to perform it is to use the Bezier curves; see [15], for example. These Bezier curves are just polynomial functions expressed in the Bernstein polynomial basis. The design parameters (or variables) are given by the nodal coordinates of the control points defining the Bezier curves. Since the design parameter r defining uniquely, in the following, the cost functional is assumed to be of the form. We discretize the shape of airfoil using one Bezier curve for upper part of airfoil and another Bezier curve for lower part. The -coordinates of the control points are evenly spaced between 0 and 1. The control points on leading edge and on the trailing edge are fixed and the other control points are moving in the -direction. The -coordinates of these control points except the control points on the leading edge and on the trailing edge are chosen to be the design parameters r. We have seven design variables in the symmetric case and fourteen design variables in the unsymmetric case. As a symmetric example, Figure 2 illustrates the Bezier curve for the upper side of the NACA0012 profile. Nine circles in the figure are Bezier control points.

For given corresponding design parameters r, pressure coefficient distribution on is:

where solves (16).

Now, the reconstruction problem reads: find the design parameter corresponding when the pressure coefficient on is known. We have chosen to formulate our reconstruction problem as a minimization problem, where we minimize an objective function measuring the difference between and the desired pressure coefficient. We define objective function to be

(17)

The reconstruction problem in a minimization problem form reads:

(18)

where U is the set of admissible design parameters. We require that U is compact and, where the design parameter r corresponds the boundary.

4. Numerical Experiments

First we do numerical experiments to demonstrate the efficiency of the algorithm in section 2. We use the Algorithm 1 to solve station Equation (16) which simulate the two-dimension incompressible inviscid uniform flows around an arbitrary given airfoil B.

We take the fictitious domain. The test problem has been solved with rectangular Eulerian mesh 80 × 80 nodes. Figure 3(a) shows the Lagrangian grids and Eulerian grids which have been used to calculate solutions for (16). In Figure 3(b), the plots in solid lines represent streamline obtained by the algorithm based on the immersed boundary.

Next we solve the reconstruction problem (18). We take the NACA0012 airfoil as. As we stated in section 3, the shape of airfoil is discretized using one Bezier curve for upper part of airfoil and another Bezier curve for lower part. Since the airfoil is symmetric during the optimization, we can take seven design variables in the optimization process. In order to keep the design acceptable, we have added box constrains for design variables. Hence, there is a lower limit and upper limit for all variables. We require that they satisfy the constraints,. The set of admissible designs U contains all

domains which are possible to obtain by using this parametrization and constraints.

We run genetic algorithm (GA) to find seven design variables in (18). The major structure of this GA (see for example [6]) is as follows: 1) Evaluation of fitness functions, 2) Roulette wheel selection, 3) Crossover, 4) Mutation. And we used the following parameters: Population size 20, Crosseover probability 0.3, Mutation probability 0.2. The above steps were repeated until the stopping criterion was satisfied. In our case the algorithm ended after a constant number of evaluations of the fitness function. The algorithm is based on function evaluations which are implemented by repeatedly solving the state Equations (16). After 2400 times of function evaluations we reached the result of optimization problem (18):

In Figure 4, Line 2 is the target design and Line 1 is the final design obtained as the result of optimization. The euclidean distance between the two lines is 0.5e−2. The computations were run on a personal computer with Intel core CPU @ 2.30 GHz and 2.0 GB RAM. One optimization takes about 5 minutes of CPU time.

Conclusion

The results of numerical experiments show that our proposed method is feasible and effective for the optimal shape design problem.

Cite this paper

Rao, L. and Chen, H.Q. (2017) The Technique of the Immersed Boundary Method: Application to Solving Shape Optimization Problem. Journal of Applied Mathematics and Physics, 5, 329- 340. https://doi.org/10.4236/jamp.2017.52030

References